高等数学教学方法探索

詹涌强

(华南理工大学广州学院 计算机工程学院，广州 510800)



高等数学教学方法探索

詹涌强

(华南理工大学广州学院 计算机工程学院，广州 510800)

为了提高学生学习高等数学课程的兴趣，培养学生的数学素质，教师在备课时需要不断的摸索，在教学中创设生动的教学情境，探索新的教学方法。作者通过几个高等数学教学案例，说明在教学中如何摸索出新的教学方法，更好地吸引学生、启发学生，提高学生的学习兴趣。

高等数学；学习兴趣；教学方法

高等数学是理工科专业的学生在大一时就要学习的一门公共基础课，它是理工科学生后续许多专业课程的基础。因此，高等数学学习的好坏对学生后继专业课程的学习起着举足轻重的作用。为了提高学生学习高等数学的兴趣，使高等数学课程学起来更加生动有趣，教师在备课的时候应该不断地摸索教学方法，创设生动的教学情境，教学中采取引导式教学与启发式教学，吸引学生的学习兴趣。下面结合笔者的教学经历从以下几个教学知识点谈谈如何更好地启发诱导学生。

1 数列极限的概念

学生学习《高等数学》[1]这门课，碰到的第一个较为抽象的概念就是数列极限的ε-N定义。把数列极限的ε-N定义讲好，将对学生学习《高等数学》后面的内容产生积极的促进作用，提高学生学习的自信心。关于数列极限的概念的讲授，作者采用了如下的方法，先给学生介绍数列的概念。

例1 观察下面4个数列的特点。

(2)2,4,8,…,2n,…

(3)1,-1,1,-1,…,(-1)n+1,…

观察这4个数列，可以发现数列(1)、(4)具有同样的特点：随着项数n的增大，数列的通项无限地接近于一个数。而数列(2)、(3)则没有这样的特点。具有(1)、(4)这种特点的数列，就是我们所关心的、所要研究的数列。

定义1：当数列{xn}的项数n无限大时，通项xn无限趋近于某一个数a，则称数列{xn}的极限是a，记作

定义1简单直观，学生对这个定义的理解没有问题。接着可向学生指出：定义1虽然简单，但有着严重的缺陷：对两个“无限”的提法不确切。什么才叫“无限大”和“无限趋近”，没有一个衡量的标准，不同的人会有不同的看法。如下面的例子：

例2 判断数列的极限。

对于(1)，学生很容易判断出这个数列的极限为1。而对于(2)，看法就各种各样：有的同学认为是0.8，有的认为是0.89，有的则认为是0.889……这时可给出几分钟的时间让学生思考。

0.8…8…=0.8+0.08+0.008+…

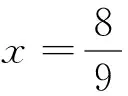
例2一方面很好地训练了学生的创新思维能力，另一方面说明定义1对数列极限的描述是不确切的。那么，如何准确地描述这两个无限：当n无限大(n→)，xn无限趋近于a(xn→a)？为了说明n→，可引入如下的语言：∃N(无论它多么大)，都有n>N；而对于xn→a，可用下面的语言描述：∀ε>0(无论它多么小)，都有|xn-a|<ε。这样就把这两个“无限”精确地表述出来了，这样就自然地得到下面定义2关于数列极限的ε-N定义。

定义2：设{xn}为一数列，如果存在常数a，对于任意给定的正数ε(不论它多么小)，总存在正整数N，使得当n>N时，不等式

|xn-a|<ε

都成立，那么就称常数a是数列{xn}的极限，或者称数列{xn}收敛于a，记为

2 复合函数求导

复合函数求导是《高等数学》[1]的一个重点内容，熟练掌握复合函数求导的方法对后面内容的学习起着重要的作用。学生在高中时就已经接触了简单的复合函数求导，知道复合函数的求导法则。

定理1 如果u=g(x)在点x可导，而y=f(u)在点u=g(x)可导，则复合函数y=f[g(x)]在点x可导，且其导数为

定理1可以推广到多个中间变量的情形。

解 本例中符合函数可分解为三个基本初等函数：y=sinu,u=tanv,v=x-5。根据复合函数求导法则有

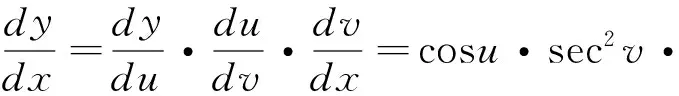
=costanx-5·sec2x-5·(-5x-6)

从本例看出，利用复合函数求导法则求复合函数的导数较为繁琐，且容易出错。是否有一种简单快捷的方法求复合函数的导数？答案是肯定的，例1也可用如下的方法求解。

=costanx-5·(sec2x-5)·(x-5)′

=costanx-5·(sec2x-5)·(-5x-6)

用这种方法求导过程就好比是脱衣服的过程，从外向内一层一层进行，形象生动，当学生熟练掌握了以后也可以一步写出结果了。而更重要的是，利用“脱衣服”的方法求复合函数的导数比求导法则更加不易犯错，如下例。

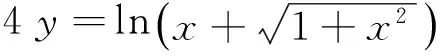
3 三角函数表的制造

学生在高中的时候就已经学会查三角函数表了，在高等数学的教学中教师可以制造一个悬念：三角函数表究竟是如何制造出来的？同学们想不想自己动手制造出一个三角函数表？从而牢牢地吸引学生的学习兴趣。教师可将三角函数表的制造分成三个部分，一步一步揭示出其中的奥秘。

第二部分介绍“函数的微分”。在讲完微分的近似计算公式以后，更进一步，学生又学会了可以利用微分近似计算公式来求出在一些特殊角30°、45°、60°等附近的三角函数值。这时，结果又揭开了一步，学生会更加地有求知欲，渴望知道其它的三角函数值是怎么计算出来的。

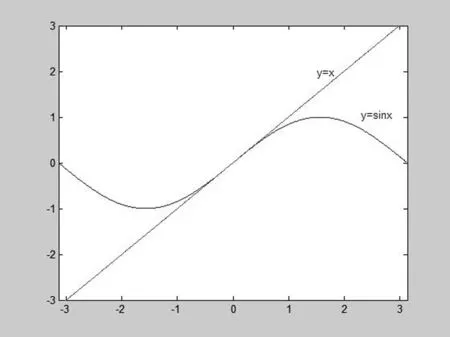
图1

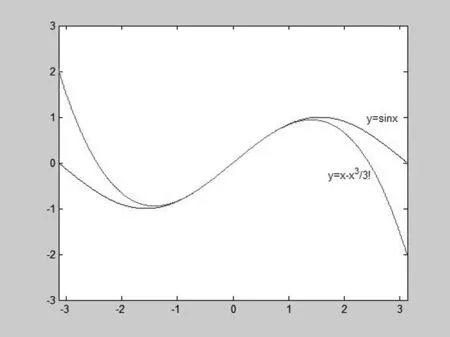
图2

图3

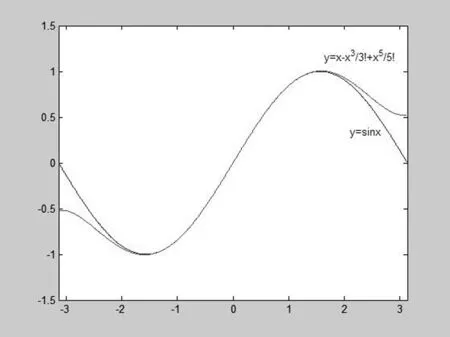
图4

从图形中，学生对多项式函数逼近正弦函数y=sinx有了一个非常清晰的直观感受，在这个时机向学生指出：在一定的条件下，可以利用多项式函数来逼近一个已知的函数，那么什么样的多项式函数才满足要求呢？多项式函数的系数是什么？从而引出泰勒公式。利用泰勒公式，可以得到各个三角函数的泰勒展式，就可以制造出三角函数表来。

[1] 同济大学数学系.高等数学：上册[M].6版.北京：高等教育出版社，2007.

[2] 赵树嫄.微积分[M].3版.北京：中国人民大学出版社，2008

责任编辑：刘 琳

Exploration on Teaching Methods of Higher Mathematics

ZHAN Yongqiang

(School of Computer Engineering， Guangzhou College, of South China University of Technology， Guangzhou 510800, China)

In order to improve interest for students to learn courses of higher mathematics and cultivate their quality of mathematics, teachers are required to constantly make explorations in the preparation for lessons, create vivid teaching situations and seek for new teaching methods. The author shows ways of groping new teaching methods to attract and inspire students, and improve their interest in learning through several cases of higher mathematics teaching.

higher mathematics; learning interest; teaching method

2016-02-27

广东省高等教育教学改革项目(GDJG20142550)；广东省教育科研类项目(2015GXJK201)

詹涌强(1978-)，男，广东潮州人，讲师，硕士，主要从事大学数学教学改革研究。

G642

A

1009-3907(2016)10-0101-04