基于改进的K-means聚类方法的多站数据关联异常检测

邵开霞，陈淡泊，周晓峰

基于改进的K-means聚类方法的多站数据关联异常检测

邵开霞，陈淡泊，周晓峰

在传统的水文时序数据研究中，我们通常只关注单个测点的时序数据，这不仅造成数据大量的冗余，还大大增加了工作的繁琐度。本文针对时间序列数据聚类的统计特征和结构特征，基于滑动窗口特征提取算法提出了改进的K-means聚类方法，来探求水文时间序列数据是否在空间上存在某种关联，并在此基础上对多水文站数据进行关联异常检测。

特征提取；K-means聚类方法；异常检测

0 引言

时间序列是一类重要的数据对象，在经济、气象、医疗等领域都普遍存在，它们具有数据量大、维数高、更新速度快等特点。近年来许多学者在时间序列的挖掘方面做很多工作，相关的研究主要集中在时间序列分割、序列聚类和分类、相似查询、模式发现等研究方向。所谓的时间序列就是一系列按照时间先后顺序记录的各个观测值。相对正常时间序列数据而言，尽管异常数据数量很少，然而这并不代表异常数据不重要，相反，这些少数的异常数据却可能隐藏着重要的信息。

聚类分析是将样本分配到不同类的过程，K-means方法是一种最经典的聚类分析方法，应用也是最为广泛的聚类方法，该方法以各类样本的质心代表该类不断迭代，只适用于数字属性数据的聚类，对超球形和凸形数据有很好的聚类效果。由于传统的K-means算法需要自己指定K值大小，存在着过分依赖经验和遍历尝试的缺点，本文引入了 AIC准则（Akaike information criterion）对数据集进行先验测试，得出可以知道K值设定的结果。

1 特征提取

本文引用基于滑动窗口的特征提取算法，它是一种词汇重组方法，通过设定一定大小的滑动窗口。该方法的定义如下：给定时间长度为 n的时间序列其中点为时刻的实际观测。此时，建立固定大小的滑窗模型对上述时间序列进行处理：定义窗口宽度为m（m远小于n）。从第一个数据开始将序列依次放入滑窗中，通过滑窗的覆盖来截取长度为 m的原序列数据，每次向右滑动一个节点以抛弃最先进入滑窗的数据，同时加入最右数据以更新滑窗内容，如此循环往复直到所有的数据都通过滑窗方法完成分割。

本文通过实验选取合适的窗口宽度，并结合领域规范或行业标准所规定的置信度要求来计算检测所需要的阈值。在此，我们假设滑动窗口分割后的子序列为：S1={（s1,t1），（s2,t2），（s3,t3），……，（sm,tm）}以此为例，首先对子序列的均值和方差两大统计特征进行介绍。因为虽然水文数据是离散的，但是它在时间维度上存在一定的延续性。子序列的平均值计算如式（1）：

方差表示数据集的离散化程度。如果两个子序列的波动程度差异很大，很显然我们很难将它们聚类到一起。子序列的方差计算如式（2）：

斜率是子序列的结构特征，是表征数据变化快慢的量，当平缓的数据里突然出现急剧波动的子序列时，我们便有充分的理由相信有某种原因或机制导致了该异常的出现。所以以计算斜率的方法来表征子序列的特征是合理的。斜率的计算如式（3）：

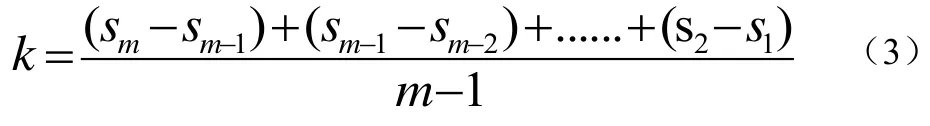
2 算法改进

2.1 改进的K-means聚类方法

与传统的静态数据相比，时间序列数据拥有更为大量、更为复杂、维度更高等特性。而在水文时间序列数据中这些特性尤为突出。通常我们采用以下两种方式来处理时间序列数据的聚类问题：一是通过改进传统得聚类算法，使之能够有效应对时序数据的复杂性；二是通加工处理时间序列数据，使之成为相似于静态数据的数据集。其实这两者的本质是相通的。

针对传统聚类算法存在的问题，本文提出了针对时间序列数据的改进的K-means聚类算法。其主要是基于时间序列数据集的结构特征相似性对比提出的。该方法的算法流程如图1所示：

图1 改进的K-means聚类算法流程图

本文通过提取数据集的统计特征结构特征，进一步对被滑动窗口分割后的子序列进行降维处理。为了能将提取出的特征值构造成三维的向量，我们将传统的K-means聚类方法拓展到三维空间中来对时序数据进行聚类。

针对传统的K-means方法需要自己指定k值的缺点，本文还引入了AIC准则对数据进行检验测试，得出k值的大小。AIC准则是衡量统计模型拟合优良性的一种标准，它建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。其伪代码如下：

我们结合经典K-means聚类算法，在获得了被滑动窗口分割后的子序列进行降维处理后的数据集后，形成了针对时序数据的改进后的K-means聚类方法。本文得到的降维处理后的数据集，每个均为三维向量，在给定K值（K＜n）的条件下，我们将原数据分成K类，即，然后求出子集中心的最小值如式（4）：

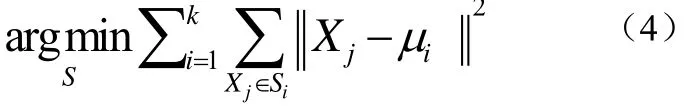
本文提出的改进方法依然沿用基于划分的主要思想，将特征提取降维的数据指定到k个相互排斥的子集中。与层次聚类不同，本文提出的方法更能够适应时间序列这种数据量比较大的数据集，而且其直接对实际观测对象进行操作，而不是对对象间距离集进行操作。

2.2 算法分析

该算法的时间复杂度主要是方差、均值、斜率的运算。除去为时序数据进行降维准备的先行算法，K-means算法本身操作的复杂度为O(nkt)，n为数据集中对象的数量。k为通过 AIC准则计算聚类的簇数的算法迭代次数，最后通过回溯算法定位原时间序列数据的异常，较为容易操作。对于时间序列数据来说，可靠的降维方式能够一定程度上保留其数据原来的复杂特征的同时降低计算的时空成本。

3 基于特征提取的聚类异常检测方法

由于水文时序数据具有绵延性质与随机性质两大特性，使得水文数据的聚类簇结合相对而言较为紧密；现假设我们对两个站点的水文时序数据进行关联异常检测，给定时间序列数据如下：

M站点水文时序数据集：

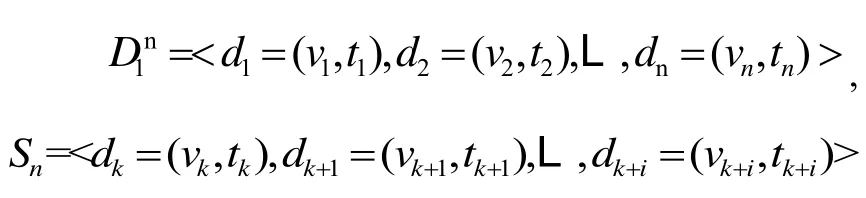
为该站的n个数据簇。

N站点水文时序数据集：

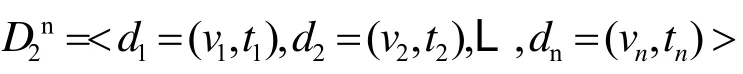
M、N站点数据经过改进的K-means算法聚类后，得出其具体的簇分布，在此，我们为方便讨论，假设M站聚类结果为两个个簇：N站的聚类结果为假设的分布位置于位置相似；与位置相似。当聚类结果进行展示时，根据中数据还原出相应时间区间，并回溯该时间区间在簇中的位置，如果出现在簇中，我们能够判断其非异常。但是，我们并不能保证还原出的时间区间中的所有数据都恰好出现在簇中，所以我们有一定理由怀疑簇存在异常性。

我们此时引入置信区间的概念：根据《水文巡测规范》，水文站数据监测可靠度要求为 95%，如果该数据集中 95%的数据为正常数据时，则很显然剩余5%的数据具有较为明显的异常性。此时，如果簇数据回溯后在簇中的概率大于设定的置信度P，则我们通过判断该簇中对象与中心对象的距离来确认异常性，取前95%的数据为正常数据，则其他簇中与簇中的数据认定为异常；反之，我们则认为仍有一定比例的正常数据在相近的聚类簇中。通过这样的方法依次检验两站通过回溯后对两站的异常检测。基于空间关系上的异常检测是相互的，所以基于M站数据对N站数据异常检测的同时，我们也必不能忽略基于N站数据对M站数据进行检测的结果，进行对比分析，得出全面合理的检测结果。

4 实验

4.1 实验环境

实验的环境配置如表1所示：

表1 实验环境配置表

4.2 数据预处理

数据规范化，指将一个低一级范式的关系模式，通过分解转换为若干个高一级范式的关系模式的集合的过程，通常我们有Max-Min归一化和均值规范化两种最常用的方法，考虑到均值规范化后的数值仍处于散乱状态无法聚集在固定的区间内，为后续实验带来不便，本文使用Max-Min归一化如式（5）：

4.3 实验过程

该实验使用某市地域相近，人工水利设施极少的M站和 N站两水文监测站的记录数据，适合进行关联分析。时间从2010年5月11号到2016年1月11号，两站分别共计五万余条数据，采集系统每小时获取一次数据，期间并无遗漏如图2、图3所示：

图2 M站水位数据

图3 N站水位数据

根据图2、图3比较，我们发现两站的数据变化及其相似，但我们并不能确定两者存在的关联关系，

因此，我们将对其进行进一步分析，判断该两站水文时序数据间是否存在某种关系。

通过对两站数据的线性相关性检验，我们得到两站数据的相关性为0.898，说明两组数据并无绝对的线性相关性。首先，我们队原时序数据进行Max-Min归一化处理，得到两站规范化后的数据集。再对两站进行 AIC准则检验，通过计算验证，M站和N站的最佳K值均为4，对应分别为接下来，我们使用改进后的K-means聚类方法对两站数据进行聚类分析，并以图像呈现，M站数据聚类图如图4所示：

图4 M站数据聚类图

N站数据聚类图如图5所示：

图5 N站数据聚类图

通过观察，我们不难发现两站数据分布极其相似，但两者的均值、方差、斜率的分布具体细节还是有很大区别，在

此，我们考虑两者是否存在可探究的弱关联关系具体数据如 表1、表2所示：

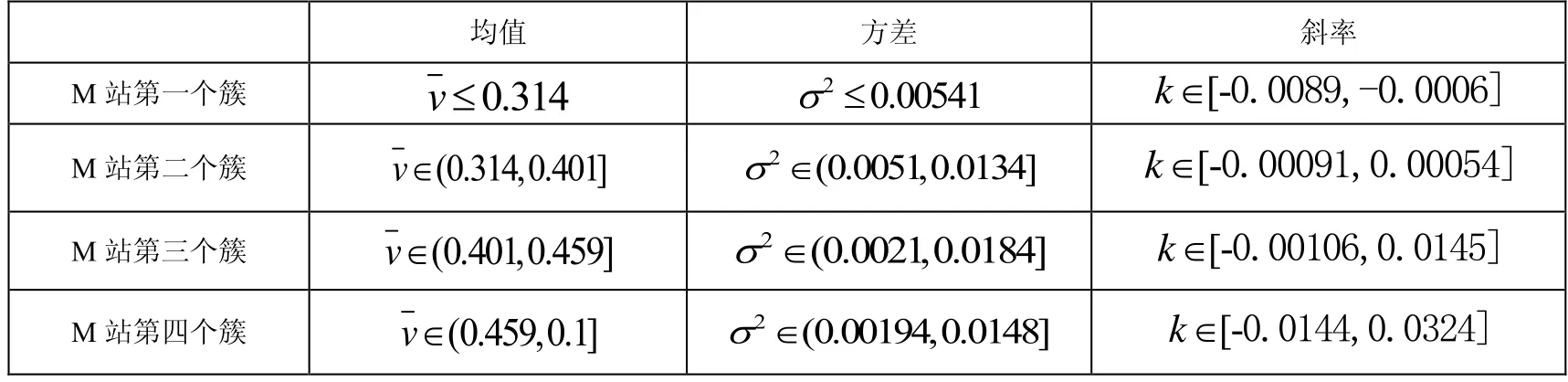
表1 M站数据特征提取数值表

表2 N站数据特征提取数值表

进行聚类的数据经过了特征提取，经过了归一化处理，我们难以带着时间维度进行精确的分析。这时候我们采用跟踪数据的方式。降维以前的一个滑动窗口大小的子序列，我们用降维以后的一个数据点代表。通过还原，我们能够很容易的得到在具体的时间点上降维以后的数据聚类的情况，同时对两站数据的聚类情况进行跟踪处理，并加以分析。

将M站数据集的聚类分为四个簇，横坐标是斜率的大小，纵坐标为均值、方差的加权平均。很容易能看出四个簇的均值、方差和斜率的变化率都依次增大。当M站聚类数据在第一簇时，该簇数据为[0.003，0.71；0.003,0.73；……；0.004；0.74]（因数据量庞大，在此仅展示少量数据）。据此，易追溯其原来降维前的时序子序列数据[7.23；7.23；7.24；……；7.26]、[7.23；7.24；7.24；……；7.26]……[8.46；8.46；8.46；……；8.72]。故而，我们可以追溯到子序列所对应的时间，以观察同时间段内，N站的数据经过降维聚类以后对应的数据簇如图6所示：

图6 簇回溯可能性分析

根据此方法，我们可以知道当M站数据簇聚集在簇1、2、3、4时，N站数据在各个簇的情况如表3所示：

表3 M、N站数据分布情况表

根据《水文巡测规范》，该水文站数据监测可靠度要求为95%，进一步进行异常检测，在以上基础上，我们对聚类结果进行进一步异常检测。

首先基于M站数据，对N站数据进行异常检测，根据表3数据可知，当置信度P为95%时，簇1中的数据为非异常数据，且仍存在5.38%的数据分布在其他簇中。此时，根据改进的K-means聚类方法衡量数据的相似度，以距离作为衡量标准，我们可以认为距离簇1的中心点距离最近的5.38%的数据为非异常数据，其他为异常数据。在所有非异常数据确认的基础上，在M站簇1里被还原出的时间区间里，则将剩余数据判定为异常数据，如图7所示：

图7 N站聚类异常分析图

然后回溯其原时间区间所对应的子序列的位置，并标定为异常即红色部分，如图8所示：

图8 N站时序异常图

图8N站时序异常图通过以上方法，我们很容易得出基于M站对N站的异常检测的其他三簇的结果，在此就不上图说明。通过四个簇的结果发现，当对各个簇分别进行聚类异常检测时，我们能够得到四个簇各自对应的异常检测结果，虽然其中有少数异常是重复出现的，但相当一部分的异常是独自出现的。我们将四簇异常结果叠加，很容易得到基于M站和N站基础上，对N站进行检测的综合聚类异常分析图和，我们继续将各类情况综合叠加，就能够得到基于M站与N站关联关系的基础上进行异常检测的N站的聚类异常分析结果与之对应的N站水文时序数据异常检测图，如图9、图10所示：

图9 N站聚类异常分析综合图

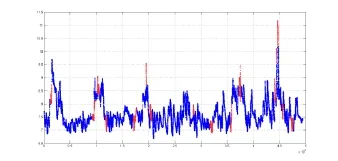
图10 N站时序数据异常检测综合图

同时，我们通过这样的方法，进一步基于N站的数据对M站的数据进行异常检测，为简化篇幅，这里我们给出其检测的最后结果如图11、图12所示：

图11 M站综合聚类分析异常图

图12 M站时序数据异常检测综合图

根据以上实验结果，我们可知两水文站数据之间虽然不存在直接的线性关联关系，但还是存在着很大意义上的弱相关性。

5 总结

本文基于滑动窗口特征提取方法提出了改进 K-means算法，与传统的聚类算法相比，本文提出的改进型K-means算法在一定程度上保留了水文时序数据集的统计特征和结构特征。本文还基于水文时间序列数据的空间关联性，在特征提取的基础上继而进行聚类操作。首先利用滑动窗口分割时序数据并获取相应的子序列集合，紧接提取其均值、方差、斜率等特征，并组合成特征向量。在此基础上进一步利用经典的K-means方法对特征向量操作聚类，形成了完整的针对水文时间序列数据的聚类方法，并在此基础上通过对聚类结果的分析完成基于多站水文数据关联关系的异常检测工作。

[1] 李深洛. 基于特征的时间序列聚类[D].桂林：广西师范大学,2014.

[2] 宋辞,裴韬. 基于特征的时间序列聚类方法研究进展[J].地理科学进展,2012,10：1307-1317.

[3] 孙友强. 时间序列数据挖掘中的维数约简与预测方法研究[D].合肥：中国科学技术大学,2014.

[4] 翁小清,沈钧毅.基于滑动窗口的多变量时间序列异常数据的挖掘[J].计算机工程,2007, 33(12)： 102-104.

[5] 余宇峰,朱跃龙,万定生,关兴中.基于滑动窗口预测的水文时间序列异常检测[J].计算机应用,2014,08：

2217-2220.

[6] 杜洪波.时间序列相似性查询及异常检测算法的研究[D].沈阳：沈阳工业大学,2008.

[7] 曲吉林. 时间序列挖掘中索引与查询技术的研究[D].天津大学,2006.

[8] 赵利红.水文时间序列周期分析方法的研究[D].南京： 河海大学硕士, 2007.

[9] 中华人民共和国水利部. SL195-2015， 中华人民共和国水利行业标准[M]. 北京： 中国水利水电出版社,

2016：4.3.8.

Multistation Data Correlation Anomaly Detection Based on Improved K- means Clustering Method

Shao Kaixia, Chen Danbo, Zhou Xiaofeng
(Department of Data Minging,Hohai University, Nanjing 21100, China)

In the study of traditional hydrological time-series data, it usually only focuses on a single point of time-series data. This not only causes a large number of redundant data, but also greatly increases the complicated degree of work. In this paper, according to the statistical characteristics and structure features of time-series data clustering, K-means clustering method which is based on feature extraction algorithm of sliding window is put forward to explore whether there is a correlation between hydrological time series data in the space, and anomaly detect the multiple hydrologic data on the basis of it.

Feature extraction； K-means clustering method； Anomaly detection

TP311

A

1007-757X(2016)11-0074-05

2016.07.29）

邵开霞（1992-），女，河海大学，硕士研究生，研究方向：数据挖掘，南京 211100

陈淡泊（1991-），男，河海大学，硕士研究生，研究方向：数据挖掘，南京 211100

周晓峰（1965-），男，河海大学，教授，研究方向：数据挖掘，南京 211100