基于隐马尔可夫和交互式遗传算法的计算机作曲算法设计

李东洋，郭为安，郑晓妹，康琦，汪镭，吴启迪

基于隐马尔可夫和交互式遗传算法的计算机作曲算法设计

李东洋，郭为安，郑晓妹，康琦，汪镭，吴启迪

“电脑音乐”自出现以来就受到广泛的关注。90年代后，越来越多的算法被应用于计算机作曲。主流的计算机作曲算法有马尔可夫转换表、遗传算法、神经网络、随机过程以及基于规则的知识库系统。提出了一种基于隐马尔科夫模型和交互式遗传算法的计算机作曲算法。通过将旋律元以及节奏融合进传统的仅以音符或节奏为单元的马尔可夫模型中，建立新型的隐马尔可夫音乐预测模型，并采用交互式遗传算法对产生音乐片段进行优化。仿真结果表明，该算法可以利用较小的数据集快速生成具有一定旋律逻辑并符合用户个性的音乐片段。

计算机作曲；隐马尔科夫模型；遗传算法；节奏；旋律元

0 引言

算法作曲（Algorithmic Composition）或称自动作曲（Automated Composition）是为了按照一定的规则将多个音乐片段组成一个有机整体的一系列的规则集合。算法作曲并不一定需要计算机，在古典时期，莫扎特就运用过随机方式来组合不同的音乐模块创作“Musical Dice Game”，并取得了良好的效果。

Markov在计算机作曲算法中是一种相对简单直接的技术。Markov转换表作曲主要针对单个音符或者和弦甚至旋律之间的联系。Bruno在其论文中提出可以利用某一特定风格的音乐作品，构造出一个Markov转换表，音符集即是该Markov模型的状态空间，从而根据Markov模型的状态转移矩阵计算下一个要出现音符的可能性[1]。Ames和 Domino的Cybernetic Composer系统对节奏也建立了Markov转换表，可以创造出摇滚乐、爵士乐及拉格泰姆乐风格的音乐片段[2]。 Karsten Verbeurgt 和Michael Dinolfo等人在训练模型中创造性的提出了音乐模式提取，在一定程度上解决了传统的一阶马尔可夫模型不能很好地描述乐曲结构的问题[3]。曹西征、毛文涛和乔锟等人提出的旋律元概念[4]。

在利用遗传算法进行作曲时，系统的适应度函数设置至关重要，黄澄宇在其研究中采用人工交互式评价，取得良好的效果[5]。

综上所述可以看出目前计算机作曲的主要技术瓶颈包括：

（1）音乐创作风格问题。

（2）音乐知识的表达问题。

（3）创造性和人机交互问题。

（4）音乐作品的评价问题。

为解决前两个问题，本文采用隐马尔科夫模型对旋律和节奏建模并加入旋律元概念，学习同一种曲风作品的方法；对于后两个问题利用交互式遗传算法进行人机交互和结果寻优。文章剩余内容主要包含以下3个方面：

（1）介绍隐马尔科夫模型基本原理，详述本文中的模型构建以及参数训练过程。

（2）建立改进的交互式遗传算法优化模型，构造出完整的作曲算法。

（3）设计仿真实验，通过对比，验证算法性能。

1 基于隐马尔科夫的音乐创作模型设计

传统的Markov链作曲是基于马尔科夫模型的作曲方法。通常学习一定量乐曲，构建以音符或者节奏为状态空间的马尔科夫模型[1,2]。然而，对音乐来说，节奏和曲调（音高起伏，即旋律）是音乐中最重要的两个要素，而且是不可分割的整体。为了简化计算，在算法研究中通常只考虑一种或少数几种音乐要素。然而目前的研究通常将所考虑的音乐要素分离开来，例如将节奏和旋律分开建模研究，这显然不满足音乐创作的需求。本文将对此改进。利用隐马尔科夫模型描述音乐的节奏和旋律关系，将二者作为关联因素进行创作。

1.1 隐马尔科夫模型（HMM）

HMM是一种时域上的统计模型。通常用来描述一个含有隐含未知参数的马尔可夫过程。在正常的马尔可夫过程中，状态对于观察者来说是直接可见的。状态之间的转换概率就是模型的全部参数。在HMM中，状态并不直接可见，但受到状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一个概率分布，因此输出符号的序列能够透露出状态序列的一些信息。因此，HMM包含两个概率矩阵，状态自身存在的转移概率矩阵和状态转移时生成或接受某个符号所对应的发射概率矩阵一个HMM中包含一下5个参数：

（1）隐含状态为式（1）：

其中n表示所有可能出现的状态个数；

（2）观察符号集合为式（2）：

其中m表示每一个状态对应的可能观察符号数；

（3）状态转移矩阵为式（3）：

其中qt表示在t时刻所处的状态；

（4）发射矩阵，即观察概率矩阵为式（5）：

其中ot表示在t时刻状态为xi的观测值；

（5）初始状态分布式（7）：

一个简单的HMM状态变迁如图1所示：

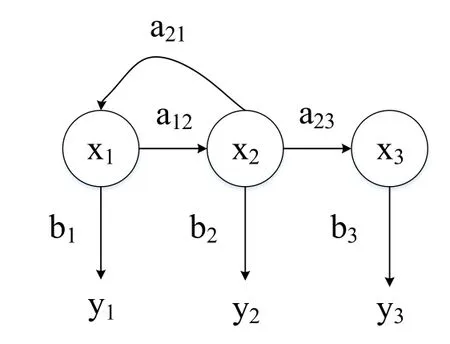
图1 HMM状态变迁图

因此，一个HMM模型，可以描述一个未知的隐含状态在已知的观察状态下的状态转移过程。也就是在模型的各参数已知的情况下，给定观察序列，去选择一个最具可能的状态序列。也就是HMM中的解码问题。本文中我们采用Viterbi算法进行求解。

1.2 Viterbi 算法

维特比算法（Viterbi algorithm）是一种动态规划算法。经常被应用于隐马尔科夫模型的解码问题中，根据已知的观察状态序列求出最有可能生成该观察状态序列的隐含状态序列。

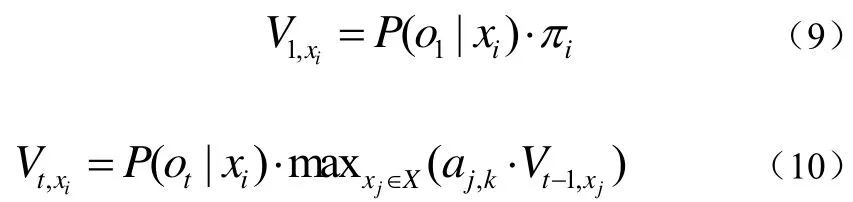
公式（10）中为前t个最终状态为xi的观测结果最有可能对应的状态序列的概率。通过保存向后指针记下在公式（10）中的状态可以获得维特比路径。另外设计一个函数，返回若t＞1时计算中的或t=1时的xi。由此可得到式（11）：

那么，根据 Viterbi算法，我们可以利用系统已知的观察状态，推断出最有可能的隐含状态。

1.3 基于节奏-旋律元的HMM创作模型设计

节奏是音乐的骨架，即使一段旋律起伏优雅动听，如果没有合适的节奏作为基础，旋律也会变得杂乱无章。对于将节奏和旋律关联考虑的问题，HMM为我们提供了良好的解决办法。本文将节奏视为HMM的观察状态，旋律为HMM中的隐含状态。首先生成一个节奏序列，而后根据这个观察序列，应用Viterbi算法产生新的旋律序列。

在以往的普通马尔可夫作曲研究中，大多是以单个音符或者音符的时长作为一个随机过程的状态空间，例如统计每个音符下一时刻出现的状态的频率作为当前状态跳转到下一个状态的转移概率。这种方法只能反映学习样本的表面结构。要表达深层结构，就必须构造更高阶的马尔科夫链，将会提升算法的复杂度，往往得不偿失。对此，本文借鉴文献[3,4]，加入旋律元的概念，提升HMM对音乐特征的表达能力。

1.3.1 基于字典树搜索的旋律元提取

为了能够在基于一阶HMM的前提下，能够最大程度地挖掘音乐知识的内部结构，本文采用旋律元与单个音符并进的学习方式。文献[4]中基于音乐规则的旋律元构建，更类似于基于知识库系统和基于音乐文法的创作模式，在一定程度上会限制旋律元的结构，并且本文前面已经提出，要构建出完整有效的音乐规则系统是非常困难的，这样，基于音乐规则的旋律元生成系统会产生许多不符合要求的旋律元。而Karsten Verbeurgt的方法中，基于字典树查询原理提取旋律元，但不对旋律元长度加以限制，将导致学习样本的几个小节同时定义为一个旋律元，这对乐曲创作的创造性设置了很大障碍。

因此，本文中定义旋律元为：在一段音乐中出现次数大于两次，并且长度在2到5个音符之间的音乐片段为旋律元。有关字典树本文不再详细介绍，具体可以参考文献[3]。我们将举例介绍如何根据字典树搜索原理提取出待学习音乐片段中的旋律元。首先我们将每一个音符的所有出现位置都视为一个根节点向下查询，直到一个根节点的所有分支都出现不同音符为止。例如一段音乐的编码为“ABCABCDE”。则根据这段音乐所构建的搜索树如图2所示：

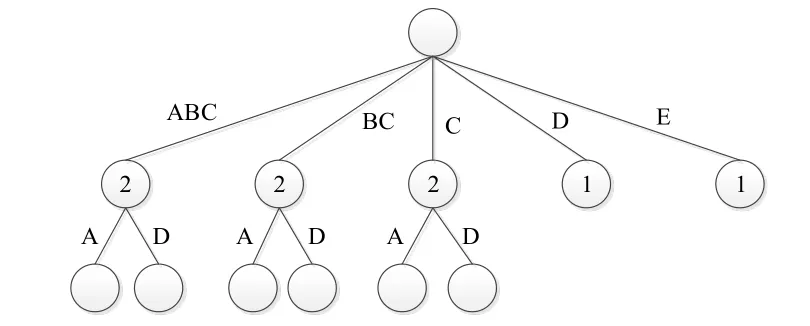
图2 根据“ABCABCDE”构建的旋律元搜索树

如图2所示，出现过两次以上的小片段总共有3个，ABC、 BC和C。但是符合出现次数大于两次，同时长度在3个到5个音符之间的音乐片段只有ABC，因此，根据本文对旋律元的定义，在这段实例音乐中，旋律元即是ABC。

通过这种方法，可以将一系列待学习音乐中的所有符合条件的旋律元全部提取出来。在训练HMM的转移概率参数矩阵时，将旋律元与单个音符融合在一起，构成描述音乐多层结构的状态空间，弥补一阶马尔科夫中存在的只能描述音乐表层的音符之间概率组合的问题。

1.3.2 HMM参数训练

综上所述，我们已经可以确定HMM的隐含状态包含待学习音乐中的单个音符以及提取出的旋律元。根据本文定义，待学习音乐的节奏为观察状态。下面需要确定的3个参数分别是：状态转移概率矩阵、发射概率矩阵以及初始概率矩阵。

在确定了模型的隐含状态之后,我们可以统计出所有状态在待学习音乐片段中出现的次数。统计一个状态（音符或者旋律元）后所有的可能状态以及这些状态出现的频率作为状态之间的转移概率矩阵。如式（12）：

发射概率矩阵，是从某个隐含状态到某个观察状态的概率。我们定义音符为隐含状态，音符所对应的时值为观察状态。那么发射概率矩阵就是统计一个音符在待学习音乐中所有可能的时值，以及它们出现的频率。计算公式与状态转移概率矩阵相同，如式（13）：

初始状态分布决定模型的初始状态。本文分别统计每个待学习音乐片段中所有音符第一次出现的位置以及出现的次数。则某一音符的初始概率为式（14）：

由于乐曲节奏的表层结构显著，通常呈现周期性，平稳性。因此，本文初始化模型的观察状态一阶马尔可夫链。以样本集中的单个时长为状态空间，状态的出现频率为初始分布概率，状态转移矩阵以公式（12）计算。为简化算法，本文将模型生成的状态序列长度限制为50。

基于HMM的作曲算法分流程图如图3所示：

图3 基于HMM的作曲算法流程图

2 交互式遗传算法优化模型

本文所提出的基于 HMM的作曲算法理论上可以产生与学习样本风格类似的音乐作品。但音乐是一个具有很强主观性感觉的产物，不同的人即是对同样的曲风的歌曲，也会有不同的感受。因此，如何使作曲算法能够产生符合使用者要求的歌曲也是需要考虑的问题。

对于此问题，本文将采用交互式遗传算法。一方面，遗传算法的交叉算子可以将产生出的音乐片段中的优秀片段保留下来，变异算子可以使乐曲突变，恰似作曲家在作曲中既借鉴优秀作品又发挥灵感的创作行为。另一方面，交互式遗传算法采用人工评价函数，可以使乐曲的进化沿着使用者的意图进行演化，达到产生符合使用者要求的目的。乐曲编码采用MIDI实数编码，考虑本文中所选取的学习样本，限制节奏编码为三十六分之一音符到全音符。定义全音符时长为单位一，节奏编码集合为：[1/32 1/16 1/8 1/4 1/2 1]。一段音乐最终将被编码为一个矩阵。例如式（15）：其中第一行为音高，第二行为节奏值。

选择算子、交叉算子分别为轮盘选择法、多点交叉。在变异算子中，采用以下3种变异方式。

（1）某一染色体中的一段音高同时升高或降低n阶，n变化范围设为[1,2,3]。如式（16）：

（2）某一染色体中的一段节奏同时升高或者降低k拍，k的取值范围为[0.25,1,1.5,2]。如式（17）：

（3）单点随机突变

突变过程中音符或者节奏值越界则随机初始化为各自状态空间中的某一状态。

本文适应度函数拟采用人工评价给出乐曲的适应度值，主导算法优化方向。为了减轻用户在算法进化过程中的试听工作量。定义一个个体的适应度值为人工评价值与基于乐曲形态特征相似度的加权和，如公式（18）：

其中，H( i)和S( i)分别是归一化后的人工评价值和基于乐曲形态特征的相似度，w为连接适应度两个部分的权重。取值规则如式（19）：

其中，n为进化代数，k∊N，N为自然数，λ和β为正整数，本文中分别取20和4。这样可以保证人工评价可以随着进化代数完全主导进化方向。w

类似的音高w节奏可以表达相近的听觉。 为1时的适应度由用户给出。 为0时，用最优个体的形态特征来衡量群体进化后的优劣，同样可以达到引导进化向用户需求方向发展的目的。本文将音符序列的形态特征符号化，上升，平稳和下降分别映射为[1,0,-1]。则利用形态特征相似度计算个体的适应度函数如式（20）：

其中l为个体的长度，SPop和Sbest分别为符号化后的种群和最佳个体。

通过适应度函数（18）。算法的终止条件为达到最大进化代数，或者用户满意。综上所述，本文所提出基于HMM和IGA的作曲算法流程图如图4所示：

图4 基于HMM-IGA的计算机作曲算法

3 实验设计及结果分析

本文基于MATLAB设计了仿真实验。训练样本为：《青花瓷》，《美人鱼》，《千里之外》和《红尘客栈》。算法参数设计如下。生成的作品长度为50个音符。基于字典树搜索提取的旋律元长度为[2,5]。IGA种群大小为 10，最大进化代数为50，交叉概率为0.8，变异概率为0.2，公式（19）中λ为20，β为4，公式（16）中n变化范围设为[1,2,3]，公式（17）中k的取值范围为[0.25,1,1.5,2]。运行十次，最优片段如图5所示：

Computer Composing Algorithm Based on Hidden Markov Model and Interactive Genetic Algorithm

Li Dongyang1, Guo Weian2, Zheng Xiaomei3, Kang Qi1, Wang Lei1, Wu Qidi1
(1. College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China；2. Sino-German College Applied Sciences of Tongji University, Shanghai 201804, China；3. The College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China)

＂Computer music＂ was widespread concerned since it had appeared. Since 1990s, more and more algorithms have been applied to ＂Computer music＂. There are five algorithms used widely for computer composing i.e., Markov chains, genetic algorithm (GA), neural network, stochastic processes and rules-based knowledge base system. This paper proposes a new computer composing algorithm based on Hidden Markov Model (HMM) and interactive GA. The new algorithm not only pays attention to the note information, but also takes the beat information and melody unit into account. Then, the new algorithm produces new music pieces based on HMM and optimizes them using interactive GA (IGA). The simulation results show this new algorithm can produce satisfied music pieces and just needs a small data set.

Computer composing； Hidden Markov Model (HMM)； Interactive Genetic Algorithm (IGA)； Beat； Melody unit

TP393.04

A

1007-757X(2016)011-0001-04

上海市自然科学基金项目（14ZR1442700）；国家自然科学基金（61503287）

李东洋（1992-），男，同济大学电子与信息工程学院，硕士研究生，研究方向：过程控制，上海 201804

郭为安（1985-），男，同济大学中德工程学院，讲师，研究方向：智能控制，智能计算，上海 201804

郑晓妹（1973-），女，上海师范大学信息与机电工程学院，讲师，研究方向：算法作曲，上海 200234

康 琦（1980-），男，同济大学电子与信息工程学院，副教授，研究方向：智能控制，智能计算等领域，上海 201804

汪 镭（1970-），男，同济大学电子与信息工程学院，教授，研究方向：智能控制，智能计算，CIMS和系统工程方面，上海 201804

吴启迪（1947-），女，同济大学电子与信息工程学院，教授，研究方向：智能控制，智能计算，CIMS和管理科学方向，上海 201804