Z规格说明的推理与验证

赵正旭，温晋杰，赵卫华

Z规格说明的推理与验证

赵正旭，温晋杰，赵卫华

Z规格说明具有非形式规约不可比拟的严谨性、清晰性。这种描述对于系统内对象的状态描述、行为描述是非常有用的原始参照物。但是，形式化描述不可避免的可能会含有错误或者是矛盾，这些问题在后期必定会导致前期的形式化设计不能付诸实践。因此，有必要做一些形式化的推理与验证来确保Z规约的实施。形式化推理是基于Z规格说明对一个操作模式求其前置条件，即求一个操作成功执行的必要条件，然后对比客观条件是否满足必要条件；形式化验证是一个操作模式求其后置条件，从集合的角度出发验证一个操作成功执行之后所导致的状态量变化是否与操作模式描述一致。

Z规格说明；推理；验证；形式化；条件

0 引言

在软件研发的过程中，面对需求越来越多变，系统越来越复杂的现状，软件需求规格说明书在软件生命周期中占有举足轻重的地位，是所有软件研发参与人员的一个可靠参照物。如何确保撰写的规格说明具有客户所要求的性质？如何确保参照该规格说明编写出的软件与规格说明书所描述的相吻合？如何保证研发人员编写出的程序的可靠性、功能性、效率性等各项质量指标呢[1]？形式化推理是验证软件正确性的重要方法之一，它通过严格的数学方法来评价一个程序是否达到了需求规格说明书所描述的功能，也就是说，对于一组允许输入的信息X，严格的证明程序能否正确执行以及能否得到正确的输出信息Z。程序正确性证明的研究早在20世纪50年代就为图灵等人所注意。一份合格的Z规格说明需要清晰准确的描述“做什么”，还必须要保证参照该规格说明编写出的软件与规格说明书所描述的各项特性相匹配。2014年在新加坡举行的第19届形式化方法国际研讨会上，有两个来自中国的团队进行了汇报，恰巧他们汇报的题目都与玉兔月球车相关，一个与月球软着陆控制器相关，另一个与玉兔月球车控制系统相关。其中用形式化方法验证玉兔控制系统切实体现了形式化方法的强大与复杂[2,3]。2015年国外一个技术团队利用形式化方法验证 Java中一些排序算法的正确性，在验证Timsort排序算法时发现了Bug。利用自动生成的测试用例集很难生成一个可以触发该 Bug的Array，所以，通过形式化推理来证明程序的正确性的时候发现了这个错误[4]。

1 Z语言概述

Z语言是一种用“数学文字”或“数学符号”来描述计算机系统的规范化语言，它不但能应用于计算机硬件系统，而且也特别适用于计算机软件系统。Z语言描述“做什么”而不涉及“怎么做”，只对目标软件系统进行功能描述。本质来讲，Z语言仅仅是一套规定的数学符号，使用Z语言所

写的“程序”是对计算机软件或硬件系统的一种抽象化设计。所以，利用Z语言写出来的内容不是计算机程序，更不是可以编译而生成能够在计算机上运行的代码。利用Z语言写出来的内容不是让计算机运行的，而是供人理解和分析的。用户可以通过这些内容去理解计算机系统的模块、数据类型、过程、函数、对象、类等，进而对计算机系统的行为、结构、逻辑进行分析、验证、改进、测试等。通俗地讲，Z语言用数学逻辑和理论模型对计算机系统进行严格的描述，形成一种抽象的设计。通常把这种设计的内容叫做计算机系统的需求规格说明，即形式化描述。与其他非形式化方法相比，Z规格说明具有以下特点。首先，Z语言不是计算机程序编制工具或编程系统，Z语言是设计规范，采用了包括集合、序列、包、关系、函数、类型、对象等抽象的数学理论。所以，Z语言是一种数学语言。其次，Z语言形成的规格说明的形式不是完全类似于ASCII码的文字和字符串，而是包括了规范化的数学符号和演算图形。Z语言形成的规格说明的内容不是能编译和运行的程序编码，而是用来进行逻辑推理和数学演算的。另外，Z语言没有完全使用数学符号来形成规格说明，它也使用了自然语言来定义变量和添加批注。所以，由Z语言生成的规格说明易于读写和解析。最后，由Z语言所形成的规格说明不仅严谨、清晰、无二义，而且可以通过形式化方法软件（如类似于Z/EVES的辅助工具）对其进行验证和推理。以下两个小节分别给出了Z规约的推理与验证方法，总体框架如图1所示：

图1 总体框架图

Z规格说明与其他方法的本质区别在于严谨以及无二义，能够最大限度保证系统的安全性。其主要研究内容为形式化的软件工程方法，贯穿于整个软件工程生命周期，包括形式化描述、形式化验证、形式化推理、形式化求精等。

2 Z规约的推理

Z语言所形成的规格说明具有非形式规约不可比拟的严谨性、清晰性，这种描述对于系统对象的状态描述、行为描述无疑是非常有用的原始参照物。但是，形式化描述也不可避免的可能会含有错误或者是矛盾，也有不满足前置条件的操作行为，这些问题在后期必定会导致前期的形式化设计不能付诸实践。另外，在操作构型内，可能有隐含的假设会导致那些不能解释操作效果的情况，也可能会出现死锁等不能容忍的状态。因此，有必要做一些形式化的推理与验证，对Z规格说明进行进一步的分析研究。形式化验证并不能完全确保系统的性能正确无误，但是可以最大限度地理解和分析系统，并尽可能地发现其中的不一致性、模糊性、不完备性等错误。Z规格说明一个主要的特点就是可以进行形式推理，这一属性对于那些高安全性和可靠性的系统来说是相当有吸引力的。

形式化推理主要是对前置条件的证明，即证明操作能够成功执行的必要条件。一个操作可以成功执行的起始状态由该操作的前置条件给出[5]。Z语言形式化推理可分为以下3步：

从描述操作模式的说明部分中删除后状态变量和输出变量；

在谓词部分中对这些变量用存在量词进行约束；

应用点规则对前置条件进行化简。

形式化推理与验证基于形式化规格说明。所以，有必要先给出一份Z规格说明书。手机通讯录应用程序是日常生活中非常熟悉的一个软件，其中新建联系人、删除联系人、修改联系人信息操作是基本操作，以下是使用微软Office Word 2007支持的Z Word Tools工具编写的对应的操作模式。

首先要确定这个应用程序要涉及到的状态变量并且对其进行命名。在这个程序中,需要定义的变量包括联系人姓名(PhoneName)和联系人电话号码(PhoneNumber)。其次，定义联系人姓名和联系人电话号码的类型分别为姓名（Name）与号码（Number）。接下来，要定义操作之后系统必须给出的提示信息。通过枚举法枚举如下：

RESPONSE：= Success|Error

利用 Z语言对一个客观事物的形式化描述的第一步就是对事物进行初始化，当然也包括对涉及到的状态变量和集合的初始化。

以下依次为初始化模式、新建联系人操作模式、删除联系人操作模式、修改联系人操作模式。

如果一个操作是有效的，那么必定存在一个正确的初始化模式。首先，对初始化模式进行推理，观察上述初始化模式，如果可以证明：

求解前置条件的一般过程如上，重复上述过程可以得到删除联系人与修改联系人信息的前置条件，如表2所示：

表2 前置条件表

3 Z规约的验证

基于 Z规格说明的形式化验证主要是对操作模式后置条件的验证，即基于离散数学的规则与概念，从集合的角度出发验证操作成功执行之后，各状态变量是否正确[6]。

操作模式 Addsuccess执行成功之后会导致电话薄中增加一位联系人，即电话薄联系人姓名集合变为原集合加上用户输入的联系人姓名，联系人电话号码集合变为原集合加上用户输入的联系人电话，利用逻辑表达式可表示如下：

对操作模式 Addsuccess验证就是利用操作模式中声明的状态变量和操作关系推导出上述三条结论。首先，证明

操作模式 Deletesuccess执行成功之后会导致电话薄中减少一位联系人，即电话薄联系人姓名集合变为原集合减去用户输入的联系人姓名，联系人电话号码集合变为原集合减去用户输入的联系人电话，利用逻辑表达式可表示如下：

对操作模式 Deletesuccess验证就是利用操作模式中声明的状态变量和操作关系推导出上述两条结论。首先，证明

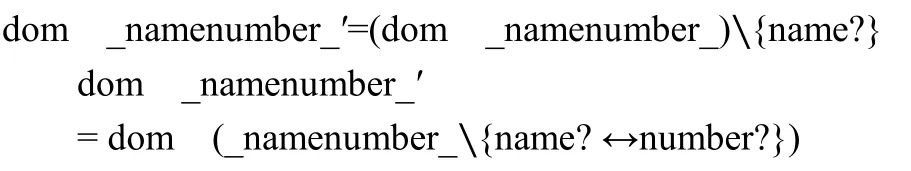
操作模式Modifysuccess执行成功之后电话薄中联系人数量不会发生变化，但是，对电话薄联系人电话号码集合进行了更新，利用逻辑表达式可表示如下：

对操作模式Modifysuccess验证就是利用操作模式中声

明的状态变量和操作关系推导出上述3条结论。首先，证明

表3 后置条件表

4 总结

形式化方法主要分为形式化规约和形式化验证两个方面。形式化规约是通过具有明确数学定义的文法和语义的方法或者语言对软件的期望特性及行为进行的精确描述。形式化验证是基于已建立的形式化规格对软件的相关特性进行评价的数学分析和证明。

程序求精是将自动推理和形式化方法相结合而形成的一门新技术，它研究从抽象的形式规格推演出具体的面向计算机的程序代码的全过程。用一个抽象程度低、过程性强的程序去代替一个抽象程度高、过程性弱的程序，并保持它们之间功能的一致。也就是说如何将Z规约转换成可执行的代码。目前。主要的策略是按照抽象程度划分层次结构，最高层为抽象程度最高的Z规约，最底层为抽象程度最低的可执行代码，中间为一系列的过度程序。对Z规约的求精或转换是推广形式化Z语言的必由环节，也是今后的一个研究重点与热点。

[1] 赵正旭, 温晋杰, 赵卫华. Z规范及其使用方法[M]. 北京：科学出版社, 2015：18-100.

[2] Hengjun Zhao, Mengfei Yang, Naijun Zhan. Formal. Verification of a Descent Guidance Control Program of a Lunar Lander[A]. FM 2014： Formal Methods [C]. Switzerland： Springer International Publishing, 2014： 733-748.

[3] Lijun Shan. Formal. Verification of Lunar Rover Control Software Using UPPAAL[A]. FM 2014： Formal Methods[C]. Switzerland： Springer International Publishing, 2014： 718-732.

[4] 百度, 形式化方法的逆袭[EB/OL]. http：//bindog. github.io/blog/2015/03/30/use-formal-method-to-find-the -bug-in-timsort-and-lunar-rover/, 2015-10-14.

[5] Jim Woodcock, Jim Davies. Using Z Specification, Refinement and Proof[M]. Oxford ： University of Oxford, 1995：201-270.

[6] J. M.Spivey.The Z Notation：A Reference Manual(Second Edition). Programming Research Group[M]. Oxford：University of Oxford,1992：156-213.

[7] 赵晓峰. 虚拟制造环境的信息规范及其Z描述研究[D].济南：山东大学. 2010.

[8] 古天龙, 常亮. 离散数学[M]. 北京： 清华大学出版社, 2012：57-83.

[9] 古天龙. 软件开发的形式化方法[M]. 北京： 高等教育出版社, 2005：159-199.

[10] 左孝凌, 李为鉴, 刘永才. 离散数学[M]. 上海： 上海科学技术文献出版社, 1982：77-95.

[11] A. Hall. Z Word Tools：Write, check, index and diagram Z specifications in Microsoft Word[EB/OL].http：//zwor dtools.sourceforge.net/, 2015-02-26.

Reasoning and Verifying of Z Specification

Zhao Zhengxu, Wen Jinjie, Zhao Weihua
(Shijiazhuang Tiedao University, Shijiazhuang 050043,China)

Compared with the informal specification, Z notion has incomparable rigorousness and clarity. The notion is an original reference for the state description and behavior description of objects in the system. However, Z notion may inevitably contain errors or contradictions, which will lead that the early formal design cannot be put into practice in the later. Therefore, it is necessary to do some formal reasoning and validation to ensure the implementation of Z notion. Formal reasoning is based on Z specification for an operator schema of its pre-condition, that is to infer the necessary conditions for the successful execution of an operation and calculates whether the objective conditions meet the necessary specifications. Formal verification is an operation mode for its post condition, from a set perspective, the verification of whether the change of the state variables caused by a successful operation is consistent with the description of the operator schema.

Z specification； Reasoning； Verification； Formalization； Conditions

TP393

A

1007-757X(2016)11-0012-05

2016.01.18）

河北省高等学校高层次人才科学研究项目（GCC2014010）；

赵正旭（1960-），男，石家庄铁道大学，教授，长江学者，博士生导师，研究方向：虚拟现实，数据组织，石家庄 050043

温晋杰（1990-），男，石家庄铁道大学，信息科学与技术学院，硕士研究生，研究方向：形式化软件工程，石家庄 050043

赵卫华（1961-），女，石家庄铁道大学，信息科学与技术学院，副教授，研究方向：信息组织，石家庄 050043