斜率匹配波形延拓法抑制EMD端点效应
李志彬,刘宏立,马子骥,李艳福,肖小兵
(湖南大学 电气与信息工程学院, 湖南 长沙 410082)
·信息科学·
斜率匹配波形延拓法抑制EMD端点效应
李志彬,刘宏立,马子骥,李艳福,肖小兵
(湖南大学 电气与信息工程学院, 湖南 长沙 410082)
提出一种抑制EMD端点效应的新方法——斜率匹配波形延拓法。该方法充分考虑了信号边缘处的变化趋势以及信号的内部特征,以信号端点处曲线的斜率作为参考,从信号内部寻找斜率最接近的子波进行匹配,根据匹配子波及其前后波形对信号端点进行波形延拓。仿真和实测信号的分析结果表明,该方法能够有效地抑制端点效应。关 键 词:经验模态分解;端点效应;斜率匹配;波形延拓
1998年,由Huang等人[1]提出的Hilbert-Huang变换(HHT)是一种信号时频分析新方法。该方法通过经验模态分解(Empirical mode decomposition,EMD),将信号分解为多个本征模态函数(Intrinsic mode function,IMF),对这些IMF分量进行Hilbert变换就可以得到Hilbert谱。EMD分解是基于信号本身的自适应分解,得到的IMF分量包含了信号真实的物理信息,其Hilbert谱反映出了信号的瞬时特征。HHT具有良好的时频分辨率,在故障诊断和信号分析等领域有着广泛的应用[2-3]。
EMD分解过程中,一个重要的过程就是构造信号的上下包络线,求出信号的瞬时平均值。通过提取信号的极大值和极小值点,分别进行三次样条插值拟合来求得信号的包络线是目前主要的处理方法。由于无法确定信号的端点是否为极值点,在进行三次样条插值拟合的过程中会出现边界摆动较大的情况,并且随着EMD的分解过程逐渐扩散到信号内部,最终破坏整个数据,造成分解结果严重失真。这就是EMD存在的端点效应问题。
目前,已有多种端点延拓方法被提出,根据改进原理,可分为极值延拓、数据预测延拓和波形延拓。极值延拓是根据信号端点附近极值点的大小和位置,在数据两端向外各延拓一定数量的极值点,此类方法有多项式拟合延拓法[4]、边界局部特征尺度延拓法[5]、极值延拓法[6]、极值斜率延拓法[7]、最小二乘-镜像延拓法[8]和极值平移法[9]等。极值延拓的算法相对简单,对抑制端点效应有一定效果。但是,仅以端点附近的极值作为延拓依据,并不能真实地反映数据本身的变化趋势。数据预测延拓的基本思路是利用信号本身的特征,采用数据序列预测的方法来向外延拓数据。此类方法有神经网络法[10]、镜像与支持向量机回归延拓法[11]等。数据预测延拓得到的结果比较准确,但算法相对复杂,计算效率低。波形延拓,是以信号内部的波形特征为依据,寻找合适的特征波在信号两端加以延拓。此类方法有边界局部特征尺度延拓法、极值延拓法和最小二乘-镜像延拓法等[4-9]。波形延拓得到的数据和原始数据有较好的一致性,但不同延拓方法对数据的选择标准也有很大的不同,效果也不一样。
本文分析了EMD方法和端点效应,对比总结了现有的抑制端点效应的方法,针对端点问题,从信号边缘的曲线走势和信号内部的波形特性入手,提出了基于斜率匹配的波形延拓法。通过仿真和实测信号的分析,与其他延拓方法进行了对比,验证了本文方法能有效抑制端点效应。
1 EMD和端点效应
1.1 EMD方法简介
经验模态分解(EMD)是把一个信号分解为若干个本征模态函数(IMF)分量之和,但每个IMF分量都必须满足两个条件,即信号的极值点与零点的个数相等或只差一个,并且根据信号的极大值和极小值得到的上下包络线,其均值为零。EMD分解就是将满足这两个条件的信号分量筛选出来。设原信号为x(t),具体步骤如下:
1)求出信号x(t)的所有极大值和极小值。
2)用三次样条插值函数分别拟合x(t)的极大值点和极小值点,求出x(t)的上下包络线。
3)求出上下包络线的均值m11(t),作为x(t)的局部均值,令h11(t)=x(t)-m11(t),把h11(t)当作原信号x(t),循环前面3步k次,得到h1,k。当h1,k满足IMF条件时,则其为x(t)的第一个IMF分量,记为c1=h1,k。
4)从原信号中减去3)中求得的IMF分量,把所得的余量信号当作原信号,循环前面4个步骤,求出其他IMF分量,即r1(t)=x(t)-c1,x(t)=r1(t)。
5)当rn(t)成为单调函数或小于某一预设值时,则原信号的EMD分解完成,分解表达式为
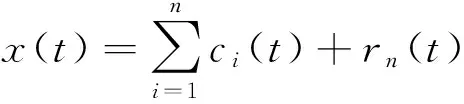
(1)
其中,x(t)为原信号,ci(t)为本征模态函数,rn(t)为残余分量。
至此,原信号被分解为若干本征模态函数和一个残余分量之和,如式(1)所示。EMD分解是一种自适应的分解方式,由数据本身出发,将原信号分解为各种不同特征波形的叠加,每个IMF分量即代表一组具有特征尺度的数据序列。
1.2 端点效应
在EMD分解过程中,需要对信号的极大值点和极小值点分别进行三次样条插值拟合来构造上下包络线。而信号端点并不一定是极值点,所以在进行三次样条插值拟合时容易在端点处出现较大摆动,并会伴随着分解过程逐步向信号内部扩散,最后造成分解得到的信号分量严重失真。
引用文献[14]中的仿真信号如式(2)所示,图1中实线为该信号原始波形,两条虚线分别为该信号的上下包络线。从图1中可以看出,由于EMD的端点效应,在拟合过程中信号的包络线在数据两端出现了严重的发散,上下包络线不能包含全部数据,由此求得的信号瞬时平均值出现误差,导致分解结果严重失真。由此可见,在进行EMD分解之前对信号进行端点处理是很有必要的。
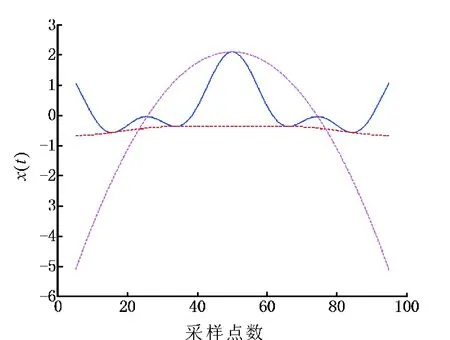
图1 信号及其上下包络Fig.1 Signal and its up and down envelope
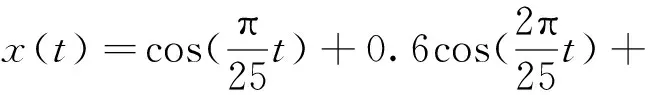
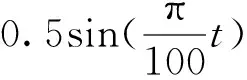
(2)
2 斜率匹配波形延拓法
对端点处的数据进行延拓,关键就是要确定原始数据在端点处的变化趋势,因此端点附近的数据是非常重要的参考。对于一个单调的曲线,其两端连线的斜率可以大致反映该曲线的走势,取信号端点和第一个极值点这两点间连线的斜率,可作为信号端点处变化的参考趋势。在原始信号的内部,以同类极值点为基准,取同方向且等长的一段单调曲线进行对比,找到与端点处的参考斜率最为接近的子波作为匹配到的波形,取该段子波前(后)端的一段数据对信号端点进行延拓,达到抑制端点效应的目的。基于此提出斜率匹配波形延拓法。
图2是基于斜率匹配波形延拓法的过程,以信号左边第一个极值点是极大值为例,S1,M1和N1分别为信号的左端点、第一个极大值点和第一个极小值点。如图2(a)所示,当S1-M1这段曲线足够长,即其包含的数据个数大于某个阈值tl时,则将其作为参考曲线;如图2(b)所示,当S1-M1这段曲线包含的数据个数小于阈值tl时,则其取M1-N1这段曲线的一半,即M1-Z1作为参考曲线。取M1-Z1是考虑到它既包含了原信号的趋势,又能增加匹配到斜率最接近子波的概率。利用参考曲线的斜率,从信号内部寻找匹配波形并取其前一段包含两个极大值和两个极小值的波形,将其延拓到S1左端。考虑到三次样条插值过程中需要用到前后各两个临近点[4],延拓两对极值点效果较好。下面以左端延拓为例,详细步骤如下:
1)求极值。设原始信号为x(t),求出所有极大值和极小值,设Emax为极大值合集,Emin为极小值合集,不妨设第一个极值点为极大值点M1。
2)提取参考曲线。计算S1-M1包含的数据个数length(S1-M1),tl表示阈值,若length(S1-M1)>tl,则取S1-M1作为参考曲线;若length(S1-M1)≤tl,则取M1-Z1作为参考曲线,计算参考曲线的斜率,记为k1。
3)求匹配子波斜率。依次从Emax中取出极大值点Mi,从Mi开始截取一段与参考曲线同方向且等长的子波,即Si-Mi或Mi-Zi。待匹配子波必须是单调曲线,否则直接判断该段子波不匹配。计算出此段子波的斜率,记为ki。求出所有匹配子波的斜率,记为集合{ki},i=2,3,…。
4)波形延拓。令kx=min(abs(k1-ki)),则第x段子波的斜率匹配成功。取Mx-2-Sx(不含Sx),将其延拓到S1左端。如果Sx左端只有一个极大值点和一个极小值点,则将这对极值点延拓两次,左端延拓完毕,否则转(5)。
5)没找到斜率匹配的子波,则参考信号边缘的极值点直接进行延拓。取信号左端两个极大值的平均值作为左端点的极大值,即M-1=M0=(M1+M2)/2;由于第一个极值点是极大值点,左端点可能比极小值还小,为了保证信号的包络线能完全覆盖信号,取信号左端两个极小值的平均值和信号左端点二者中较小的一个作为左端延拓的极小值,即N-1=N0=min(X(1),(N1+N2)/2),左端延拓完毕。第一个极值点是极小值点的情况类似。
右端延拓方法和左端类似。在实验中,阈值tl取3的效果较好,在工程应用中可根据实际情况进行调整,tl取越大,越趋向于取到第二段曲线来进行斜率匹配。
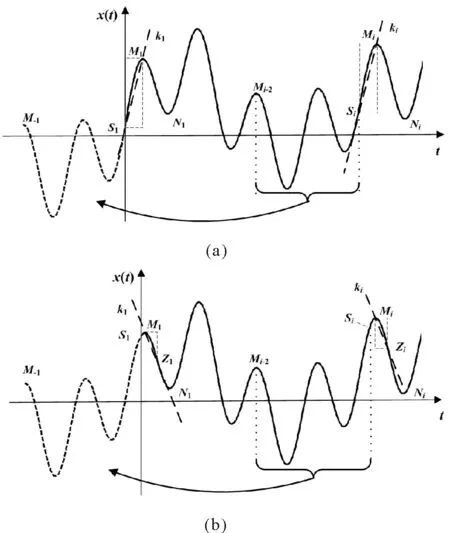
图2 基于斜率匹配的波形延拓法Fig.2 The border slope matching process
3 仿真信号分析
为了方便分析比较,引用文献[17]中的调频调幅非线性仿真信号,其表达式为
x(t)= sin(2π120t)+
(1+0.2sin(2π7.5t))×
cos(2π30t+0.5sin(2π15t))。
(3)
式中采样频率为1 000Hz,采样点数为250点,原信号及其组成分量的波形如图3所示。
图4是式(3)中的信号没有进行端点处理直接进行EMD分解的对比图,上图和中图的实线是分解得到的IMF分量,虚线是原信号分量。下图是两个IMF分量和对应原信号分量的绝对误差。可以看出,没有进行端点处理得到的IMF分量,在数据两端出现了大幅度摆动,相比原信号分量已经有较大误差。

图4 无延拓的EMD分解结果和误差Fig.4 No extension of EMD decomposition results and error
图5是用斜率匹配波形延拓法处理之后的EMD分解结果与原信号进行对比。相比之前没有延拓直接分解的情况,延拓后的分解结果,其IMF分量在端点附近的摆动大幅度减小,与原信号分量相比也基本吻合,误差很小,说明本文方法对端点效应有很好的抑制作用。
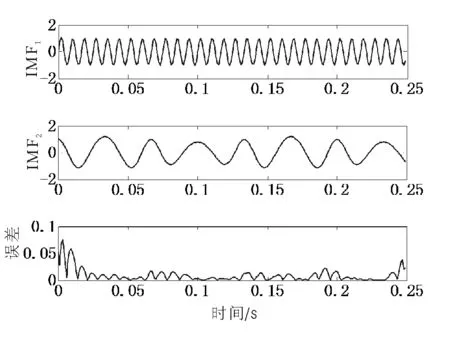
图5 斜率匹配法EMD分解结果和误差Fig.5 The EMD decomposition of slope matching and error
为了评价抑制效果的好坏,参考文献[18-19],采用以下两个指标来评价端点效应的处理效果:
1)EMD分解所得的各个IMF分量和对应原信号分量之间的相似系数ρ,通过与原信号分量比较相似度来评价抑制效果,
ρi(xi(t),IMFi(t))=
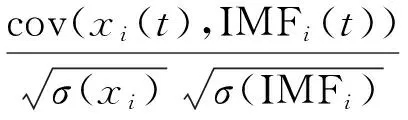
(4)
式中,cov()表示协方差;σ()表示方差;IMFi表示信号EMD分解的第i个分量;xi为相应的原始信号分量。ρ的值越接近于1,则说明端点效应的抑制效果越好。
2)EMD分解所得的各个IMF分量和对应原信号分量之间的平均误差为
error_IMFi=
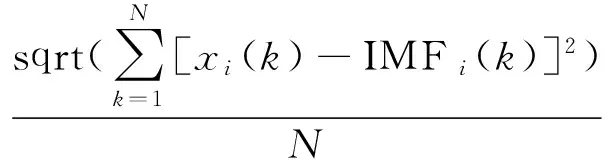
(5)
式中,N表示信号的总个数;xi(k)表示原信号的第i个分量;IMFi(k)表示EMD分解后得到的对应分量。error_IMFi越接近于0,则说明端点效应的抑制效果越好。
采用前文提到的其他延拓方法分别对式(3)进行端点延拓和EMD分解,计算出各自的评价指标进行对比分析,对比结果如表1所示。

表1 端点效应抑制效果评价表
由表1中的参数可以看出,波形匹配延拓法对端点效应的抑制效果最好,其次是斜率匹配波形延拓法和极值延拓法,这3种方法得到的相似系数相对较大,分解误差较小,能够有效地抑制端点效应。最小二乘-镜像延拓法、镜像延拓法和边界局部特征尺度延拓法对本例的处理效果并不是很理想,相似系数不高,分解误差相对较大,如果要在实际工程中应用还需要加以改进。
4 实际信号分析
对于现实中的非平稳随机信号,使用本方法进行延拓也能有效地抑制端点效应。图6(a)是一段电力线载波信号,数据来源于湖南大学13舍实验楼七楼配电箱A相的一段测量记录,使用的示波器型号为Tektronix-DPO3034,采样频率为250kHz。电力线载波信号[20]中存在各种电力噪声,是一种非平稳的随机信号,对该信号使用本文方法进行端点延拓和EMD分解,得到的结果如图6(b)所示,而图6(c)则是无端点延拓直接进行EMD分解的结果。
对比图6(b)和图6(c)可以看出,没有进行端点处理的EMD分解得到了一些没有意义的分量,信号的发散现象严重,部分IMF分量的幅值还超过了原信号数倍。而采用了基于斜率匹配波形延拓法的EMD分解结果则很好地抑制了端点效应,成功将信号分解成从高频到低频的多个IMF分量。
为了进一步验证本文方法的准确性,采用前文提到的其他延拓方法对该信号进行端点延拓和EMD分解。由于端点效应对高频IMF分量的影响不明显,为了便于比较,只取分解结果的最后4个IMF分量进行对比,结果如图7所示。
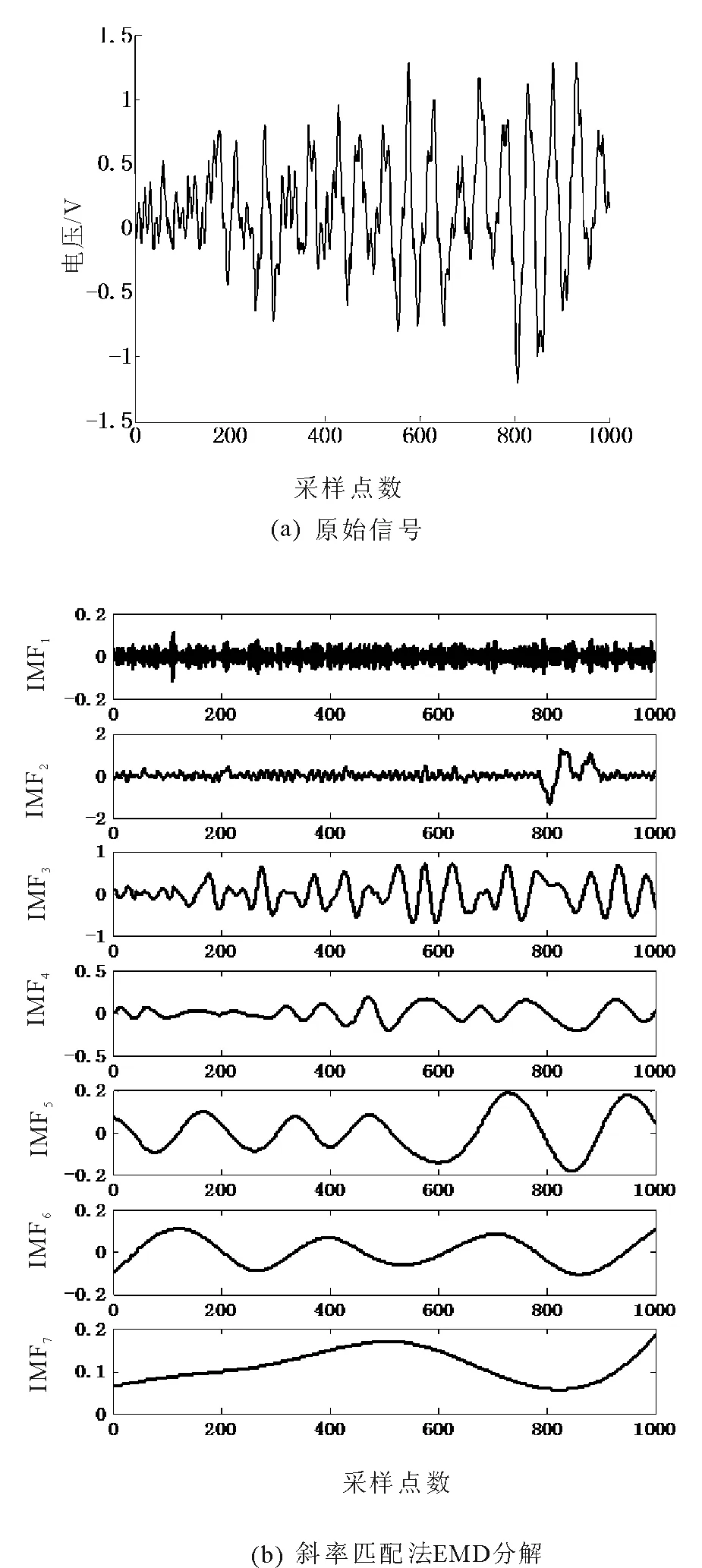

图6 电力线载波信号EMD分解Fig.6 Power line carrier signal EMD decomposition
从6种延拓方法的分解结果对比可以看出,斜率匹配波形延拓法、镜像延拓法、最小二乘-镜像延拓法和自适应波形匹配延拓法都得到了比较理想的分解波形,较好地抑制了端点效应的产生;而极值延拓法等其他几种方法的分解效果并不理想,比较明显的是出现了部分IMF分量的幅值超过原信号数倍的情况,可见端点问题已经影响到了信号内部,分解结果已经失真。表2列出了几种延拓方法EMD分解所用时间,从表2可以看出,本文方法所用的时间最少,算法效率相对较高。
综合分析3类延拓法,极值延拓法只关注信号边缘附近的极值点,没有考虑信号内部的特性,实际应用中计算精度较低,适应性较差;诸如神经网络延拓的数据预测法的算法复杂,计算效率较低,实际工程应用很少,因此本文没做比较;波形延拓法在考虑了原始信号的特征趋势后对数据加以延拓,对于抑制端点效应的效果较好。通过仿真和实测信号分析,斜率匹配波形延拓法在保证EMD分解结果正确的同时,能节省更多时间和资源,计算精度和效率较高,适应性强,优于其他方法。
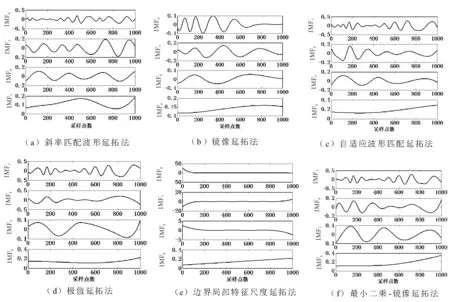
图7 不同方法的电力线载波信号EMD部分分解结果Fig.7 Part of the power line carrier signal EMD decomposition with different methods

5 结 论
本文提出了一种基于斜率匹配波形延拓法的抑制EMD端点效应的方法。通过计算信号端点处曲线的斜率作为信号端点的趋势,从信号内部找到斜率最为接近的子波作为匹配波形,通过该子波对信号端点进行波形延拓,有效抑制了三次样条插值拟合时出现的发散问题。同时,本方法充分考虑了数据边缘处的发展趋势及其与数据内部存在的联系,从而最大限度地保证延拓后的数据与原数据具有最接近的趋势。不论是仿真信号还是实际信号,通过斜率匹配延拓后的波形都能得到较好的EMD分解结果,计算效率和效果也优于其他延拓方法,符合工程应用的要求。
[1] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [C].Proceeding of the Royal Society of London A:Mathematical, Physical and Engineering Science.The Royal Saiety,1998:903-995.
[2] VINCENT H T, HU S L J, HOU Z. Damage detection using empirical mode decomposition method and a comparison with wavelet analysis[C]∥Proceedings of the 2nd International Workshop on Structural Health Monitoring. Standford,1999:891-900.
[3] YU Dejie, CHENG Junsheng, YU Yang, et al. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings[J]. Mechanical Systems and Signal Processing,2005,19(2):259-270.
[4] 王红军, 付瑶. 基于多项式拟合的EMD端点效应处理方法研究[J]. 机械设计与制造, 2010(10): 197-199.
[5] 黄诚惕.希尔伯特-黄变换及其应用研究[D].成都:西南交通大学,2006.
[6] 黄大吉, 赵进平, 苏纪兰. 希尔波特-黄变换的端点延拓[J]. 海洋学报, 2003, 25(1): 1-11.
[8] QINGJIE Z, HUAYONG Z, LINCHENG S. A new method for mitigation of end effect in empirical mode decomposition[C]∥Informatics in Control, Automation and Robotics, 2010 2nd International Asia Conference on. IEEE, 2010, 1: 400-403.
[9] 王学敏, 黄方林. EMD端点效应抑制的一种实用方法[J]. 振动.测试与诊断, 2012, 32(3): 493-497.
[10] 胡劲松, 杨世锡. EMD方法基于径向基神经网络预测的数据延拓与应用[J]. 机械强度, 2008, 29(6): 894-899.
[11] LIN D C, GUO Z L, AN F P, et al. Elimination of end effects in empirical mode decomposition by mirror image coupled with support vector regression[J]. Mechanical Systems and Signal Processing, 2012, 31: 13-28.
[12] 韩建平, 钱炯, 董小军. 采用镜像延拓和RBF神经网络处理EMD中端点效应[J].振动.测试与诊断, 2010, 30(4): 414-417.
[13] 胡爱军, 唐贵基, 安连锁. Hilbert-Huang变换边界问题处理方法研究[J]. 机械强度, 2008,30(5): 739-743.
[14] 邵晨曦, 王剑, 范金锋, 等. 一种自适应的EMD端点延拓方法[J]. 电子学报, 2007, 35(10): 1944-1948.
[15] 李钊, 周晓军, 徐云. 基于均生函数周期叠加外推法的EMD端点问题的研究[J]. 振动与冲击, 2013, 32(15): 138-143.
[16] 王婷,杨莘元,李冰冰. 一种改善EMD端点效应的新方法[J]. 哈尔滨理工大学学报,2009,14(5): 23-26.
[17] 祁艳杰, 王黎明, 杨泽辉, 等. 几种改善EMD端点效应方法的比较研究[J]. 现代电子技术, 2013, 36(22): 50-52.
[18] 王婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨:哈尔滨工程大学.2010.
[19] 林丽, 周霆, 余轮. EMD算法中边界效应处理技术[J]. 计算机工程, 2009, 35(23): 265-268.
[20] 魏春娟. 低压电力线载波通信的应用与发展[J]. 低压电器, 2011(9): 45-49.
(编 辑 李 静)
Slope matching waveform extension method suppressing the EMD end effect
LI Zhibin, LIU Hongli, MA Ziji, LI Yanfu, XIAO Xiaobing
(College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)
A new method is proposed to inhibit the end effect——slope matching wave extension method. The method takes the endpoint slope of signal as reference and finds the closest matching wavelet from the signal, then it extends the wave of signal endpoint according to the matching wavelet. Analysis of the simulation signal and measured signal showed that the method can effectively inhibit the end effect.
EMD; end effect; slope matching; wave extension
2016-03-11
中央国有资本经营预算项目(财企[2013]470号);中央高校基本科研基金资助项目(2014-004);国家自然科学基金资助项目(61172089)
李志彬,男,福建漳州人,从事数字信号处理研究。
TN911.7
A
10.16152/j.cnki.xdxbzr.2016-05-010

