整数幂模p剩余的差的均值

吕 叶，徐哲峰

(西北大学 数学学院， 陕西 西安 710127)



·数理科学·

整数幂模p剩余的差的均值

吕 叶，徐哲峰

(西北大学 数学学院， 陕西 西安 710127)

设p是奇素数, l,m为满足l≢m(mod p-1)的正整数，利用三角和的方法研究了整数的m次幂模p剩余与l次幂模p剩余之差的2k次均值，并得到渐近公式。

m次幂模p剩余；均值；三角和；渐近公式

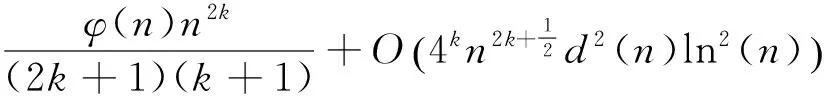
S(n,δ)=#{a:1≤a≤n-1,(a,n)=1，

并给出了

S(n,δ)=

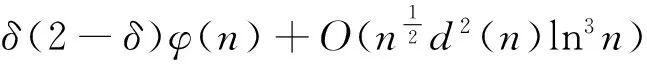
Sm,n,λ,δ={a:1≤a≤λn,(a,n)=1,|a-(am)n|≤δn}。

在文献[3]中，徐哲峰对|a-(am)n|的均值分布问题进行了深入的研究，推广了文献[1-2]中的结论，获得了如下的渐近公式

其中ω(n)表示n的不同素因子的个数。

本文对文献[3]中的问题进行了一种推广，利用三角和方法研究了整数m次幂模p剩余与l次幂模p剩余之差的2k次均值，获得了一些较强的渐近公式。主要结论如下。

定理1 设p是奇素数，k为非负整数，l,m为满足l≢m(mod p-1)的正整数，则有渐近公式

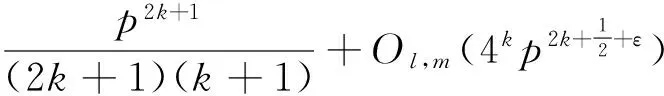
在定理1中取l=1，便获得了文献[3]中当λ=δ=1，n=p且k为偶数时的相应结论，即如下的推论。

推论1 设p为奇素数，m≥2为整数，则有渐近公式

推论1 设p为奇素数，k为非负整数，则有渐近公式

1 一些引理

引理1 设p为奇素数，l为正整数，r为满足1≤r≤p的整数，则有

其中e(y)=e2πiy。

证 明 参见文献[3]引理3。

引理2 设q≥1及t≥2均为整数，多项式f(x)=a1xr1+…+atxrt，其中r1,…,rt为一组不相等的非零整数，且满足(a1,…,at, q)=1，则有估计式

证 明 参见文献[4]定理1。

引理3 设s,r为满足1≤s,r≤p-1的整数l,m为满足l≢m(mod p-1)的正整数，则有如下估计式

证 明 因为1≤s,r≤p-1，所以(s,r,p)=1，又因为l≢m(mod p-1),则由引理2可得

引理4 设a,b为整数，p为奇素数且a,b,p满足p⫮(a,b)，则对任意的满足m≥2,α≥1的整数有

其中，ω(n)表示n的不同素因子的个数。

证 明 参见文献[3]引理1。

引理5 设r,s为整数l,m为满足l≢m(mod p-1)的正整数，则有如下的两个估计

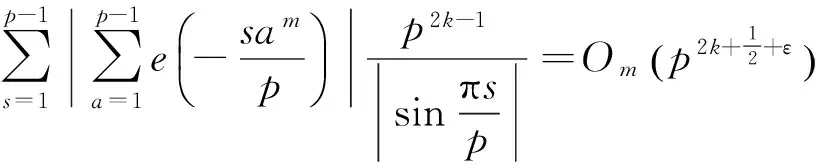
(1)

(2)

证 明 首先来完成式(1)的证明。

(i)当m≥2时，在引理4中令b=p,α=1可得

则有如下估计

然后利用Jordan不等式

可得

(3)

(ii)当m=1时，由于p⫮s，则

同理可得

(4)

那么，由式(3) (4),可得对任意正整数m，有

这便证明了引理5中式(1)的结论。

现在来完成引理5中式(2)的证明。

由引理3和Jordan不等式可得

2 定理1的证明

这个部分我们来完成定理1的证明。首先，由三角不等式得到

Ω+Ψ+Υ+θ。

现在我们来逐个处理每一项。首先计算Ω。利用引理2可得

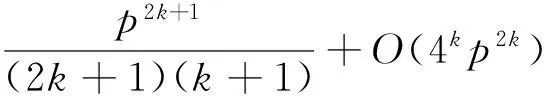
其次估计Ψ。由引理1有

由式(1)可得

同理可得

下面我们来估计θ。利用引理1，有

θ=

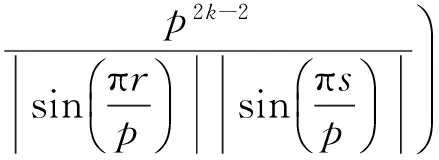
由引理5的式(2)可得

结合以上关于Ω,Ψ,Υ,θ的结果可得

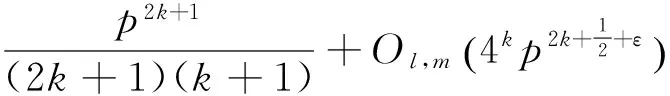
这样就完成了定理1的证明。

[1] ZHANG W.On the difference between an integer and its inverse modulon[J].Number Theory,1995,52:1-6.

[2] ZHANG W.On the distribution of inverses modulon[J]. Number Theory, 1996,61(2):301-310.

[3] XU Z.Distribution of the difference of an integer and itsm-th power modnover incomplete intervals[J]. Number Theory，2013,12(12):4200-4223.

[4] SHPARLINSKI I.On exponential sums with sparse polynomials and rational functions[J].Number Theory, 1996,60(2):233-244.

[5] BECK J， KHAN M R.On the uniform distribution of inverses modulon[J].Period Math Hungar，2002，44：147-155.

[6] COBELI C， ZAHARESCU A. On the distribution of the Fp-points on an affine curve inrdimensiona[J]. Acta Arith，2001，99：321-329.

[7] COCHRANE T， ZHENG Z. Upper bounds on a two-term exponential sum[J].Sci China Ser A，2001，44：1003-1015.

[8] 徐哲峰,易媛.不完整区间上整数及其逆的差[J].中国科学: 数学, 2011,8：669-679.

[9] FORD K， KHAN M R， SHPARLINSKI I E，et al.On the maximal difference between an elementand its inverse in residue rings[J].Proc Amer Math Soc，2005，133：3463-3468.

[10] KHAN M R，SHPARLINSKI I E. On the maximal difference between an element and its inverse modulon[J].Period Math Hungar，2003，47：111-117.

(编 辑 亢小玉)

The mean value of the remainder of the integer power modp

LÜ Ye， XU Zhefeng

(School of Mathematics, Northwest University, Xi′an 710127， China)

Letpbe an odd prime, letl,mbe integers withl≢m(modp-1), this paper uses the method of triangle sum to study the 2k-th power mean value of the difference of the integer′sm-th power modpresidual and itsl-th power modpresidual, and then get the asymptotic formula.

m-th power modp; mean value; triangle sum; asymptotic formula

2016-02-26

国家自然科学基金资助项目(11471258)

吕叶，女，陕西宝鸡人，从事基础数论的研究。

O156.4

A

10.16152/j.cnki.xdxbzr.2016-05-001