概率优势关系下的粗糙集模型及属性约简

施玉杰, 杨宏志, 魏 玲

(1.郑州大学 数学与统计学院， 河南 郑州 450001;2.河南财经政法大学 河南 郑州 450046;3.西北大学 数学学院, 陕西 西安 710127)



·数理科学·

概率优势关系下的粗糙集模型及属性约简

施玉杰1, 杨宏志2, 魏 玲3

(1.郑州大学 数学与统计学院， 河南 郑州 450001;2.河南财经政法大学 河南 郑州 450046;3.西北大学 数学学院, 陕西 西安 710127)

针对序信息系统,提出了一种新的优势关系,并探讨了概率优势关系粗糙集模型及其性质;定义了概率优势类结构差异度的概念,给出一种概率优势关系下的属性约简理论及算法。为基于优势关系序信息系统的知识发现提供了新的方法和思路。

序信息系统;概率优势关系;粗糙集;属性约简

粗糙集理论是波兰数学家Pawlak教授于1982年提出的一种处理具有不精确、不确定和模糊性的数学工具[1-2],已经广泛用于人工智能、机器学习、决策支持和分析、数据挖掘、知识发现等领域,并取得了丰硕的研究成果[3-7]。经典粗糙集理论主要以等价关系为基础,比较适合处理分类问题。然而在实际问题中,有些信息系统中属性取值是可比较的,涉及多属性决策领域的比较与排序问题,此时使用等价关系就不能获得很好的结论。于是,Greco,Slowinski等人拓展了粗糙集理论,提出了基于优势关系的粗糙集理论[8-11]。近年来,很多学者对优势关系下的信息系统进行了大量深入的研究,其中优势关系下属性约简问题也越来越多地受到关注[12-16]。

以往研究序信息系统时使用的优势关系是比较严格的,要求可比较的对象在所有属性取值上都大于或等于,这种定义对噪声十分敏感,且得到的优势类比较有限,可能导致很多对象在多属性下无法比较。文献[17]定义了一种概率优势关系,研究基于该关系下的排序问题,并把这种方法应用于实际问题。但是，该文献中定义的优势关系还有改进的空间。此外,概率优势关系下粗糙集的性质及属性约简问题目前研究甚少。

针对传统优势关系要求过于严格,及目前概率优势关系研究的不完善等问题,本文改进已有的概率优势关系,使之更加合理,并分析探讨了概率优势关系粗糙集模型的一些性质。进而引入概率优势类结构间差异度的概念,并给出相应的性质和结论,在此基础上给出概率优势关系下序信息系统属性约简的理论与方法,丰富了基于优势关系下序信息系统中知识发现的研究。

1 概率优势关系

首先介绍传统序信息系统中的优势关系,然后给出改进后的概率优势关系。

定义1[4]一个信息系统是一个四元组I=(U，AT， V, f ),U是非空有限的对象集;AT是非空有限的属性集; f: U×AT→V为关系函数,它表示U中每一个对象的属性取值,V=∪a∈ATVa为属性值域。

在信息系统中,如果某属性取值是递增或者递减的关系,则该属性称为一个准则;由若干准则组成的集合称为准则集。如果一个信息系统的所有属性都是准则,则被称为序信息系统[18]。因递增和递减的关系仅由所考察准则的意义决定,对理论研究并无影响,为表述方便,本文只针对递增的优势关系进行研究。

定义2[4]在序信息系统I=(U, AT, V, f)中,对于A⊆AT,属性子集A对应的优势关系表示为:

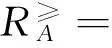
对象x在属性集A下所对应的优势类为:

该定义中的优势关系要求在每一个属性下都成立,条件过于严格,导致一些对象之间无法比较优劣。而概率优势关系的提出能有效地弥补这一缺陷,从而为深入研究优势关系下的序信息系统提供新的方法。

定义3[17]设序信息系统I=(U, AT, V, f),∀x,y∈U,a∈AT,记

pa(x, y)称为对象x与y在属性a下的二值判断,若pa(x, y)=0,表明在属性a下,y的取值一定小于x,相应地,pa(x, y)=1表明y在属性a下的取值不小于x的取值。

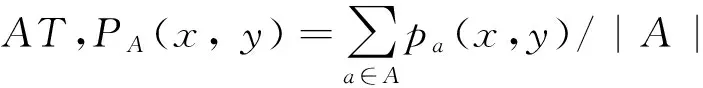
其中|A|表示属性集A中的属性个数。PA(x, y)的全体PA=[PA(x, y)]n×n称为I在A下的二值判断频率矩阵,简称判断矩阵。

定义5[17]设序信息系统I=(U, AT, V, f),对于A⊆AT,给定阈值α,那么该序信息系统在属性子集A下的α概率优势关系定义为:

对象x在属性集A下的α概率优势类定义为:

然而该定义下有些对象的优势类不是十分合理,比如,一个序信息系统中,对象x在4个属性下的取值为 (1, 2, 1, 1),对象y在4个属性下的取值为(1, 1, 1, 1),按照定义5中给出概率优势关系及优势类,只要满足阈值小于0.75,都能得到y在x的优势类中,而事实上y并不优于x。因此上述概率优势关系还可进一步改进。下面我们给出改进后的α概率优势关系及优势类。

定义6 设序信息系统I=(U, AT, V, f),对于A⊆AT,给定阈值α,该序信息系统在属性子集A下的α概率优势关系定义为:

PA(x, y)≥PA(y, x), 0.5≤α≤1};

对象x在属性集A下的α概率优势类表示为:

显然定义6中，若α=1,则退化为定义2的优势关系,所以上述概率优势关系是传统优势关系的一种推广。

2 概率优势关系下粗糙集模型及性质

针对序信息系统,概率优势关系下的粗糙集模型有一些好的性质和结论成立。

性质1 设序信息系统I=(U, AT, V, f),对于属性集A⊆AT,给定阈值α,由概率优势关系及概率优势类的定义,易知有以下性质:

性质2 设序信息系统I=(U, AT, V, f),A⊆AT,则定义7给出的α概率优势关系下的上近似和下近似满足以下性质:

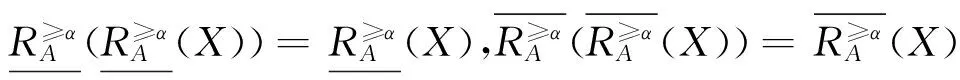
这些性质可根据定义6及定义7证得。

3 基于概率优势关系的属性约简

序信息系统属性约简问题是粗糙集理论研究的热点之一,本节我们探讨概率优势关系下序信息系统属性约简的问题。

3.1 概率优势关系下优势类结构差异度

在序信息系统中,传统优势关系和优势类之间满足单调性,也即属性个数越多,其对应的优势关系及优势类就越小。但概率优势关系下该性质不再适用。因此以往寻找属性约简的方法在概率优势关系下有一定的局限性。然而引入概率优势类结构差异度来寻找概率优势关系下序信息系统的属性约简能有效地避免因不满足单调性引起的弊端。

定义8 设 I=(U, AT, V, f)为一个序信息系统,∀A, B⊆AT,给定阈值α(0.5≤α≤1),

定义9 设序信息系统I=(U, AT, V, f),属性集A, B⊆AT,给定阈值α,∀x∈U,对象x在属性集A, B下的α概率优势类结构差异度定义为:

简记为s(≥A,≥B)。其中Δ为集合之间的对称差运算,即AΔB=(A-B)∪(B-A),|·|为集合的基数。

性质3 设序信息系统I=(U, AT, V, f),A, B⊆AT,给定阈值α,则0≤s(≥A,≥B)≤1。

性质4 设序信息系统I=(U, AT, V, f),∀A, B⊆AT,给定阈值α,有0≤S (≥A, ≥B)≤1。

该性质由定义10及性质3可证。

3.2 概率优势关系下的属性约简

定义11 设I=(U, AT, V, f)为一个序信息系统,给定阈值α,若对于A⊆AT,满足:

则称属性子集A是序信息系统I在α概率优势关系下的一个约简。若仅满足(1),则称A是序信息系统I在α概率优势关系下的一个协调集。

定理1 设序信息系统I=(U, AT, V, f),给定阈值α,∀A, B⊆AT,S (≥A,≥B)=0的充分必要条件为

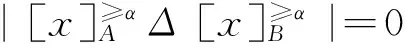
该定理说明序信息系统中,两个属性集合间的概率优势类结构差异度为0，等价于它们具有完全相同的概率优势类。

结合定义11及定理1,我们可以得到关于概率优势关系下序信息系统属性约简的判定定理。

定理2 设序信息系统I=(U, AT, V, f),给定阈值α,若对于A⊆AT,有S (≥A, ≥AT)=0,且∀a∈A,有S (≥A-{a}, ≥AT)>0,则属性集子集A为α概率优势关系下序信息系统的一个约简。

3.3 概率优势关系下的属性约简算法

利用上一节概率优势关系下序信息系统约简的定义及判定定理,本节给出一种概率优势关系下寻找属性约简的算法。

输入:信息系统I=(U, AT, V, f),对象集U=(x1, x2, …, xn),属性集AT=(a1, a2, …, am),给定阈值α(0.5≤α≤1)

输出:概率优势关系下序信息系统属性约简C

Step1 令A0=∅,i=1;

Step2 ∀a∈AT-Ai-1,依次计算S(≥Ai-1∪{a}, ≥AT),找到S(≥Ai-1∪{a}, ≥AT)取值最小时对应的a,令Ai=Ai-1∪{a}；

Step3 若S(≥Ai, ≥AT)=0成立,转Step4，否则,i=i+1,转Step2;

Step4 ∀a∈Ai,若S(≥Ai-{a}, ≥AT)>0,则转Step6;

Step5 若∃a*∈Ai,S(≥Ai-{a*}, ≥AT)=0,删除属性a*,Ai=Ai—{a*},转Step4;

Step6 算法结束,输出约简C=Ai。

该算法的主要思想是通过逐步添加属性来寻找协调集,每次添加的属性都能保证与属性全集间的概率优势类结构差异度最小,直至结果为0，即找到了一个协调集;进而再根据定理2判断此时的协调集是否为约简。该算法能确保所找到的约简属性个数最少。

例1 表1是文献[12]中给出的一个序信息系统,其中对象集U=(x1, x2, …, x5),属性集AT=(a1, a2, a3, a4),下面根据上述算法求α概率优势关系下序信息系统的一个约简。

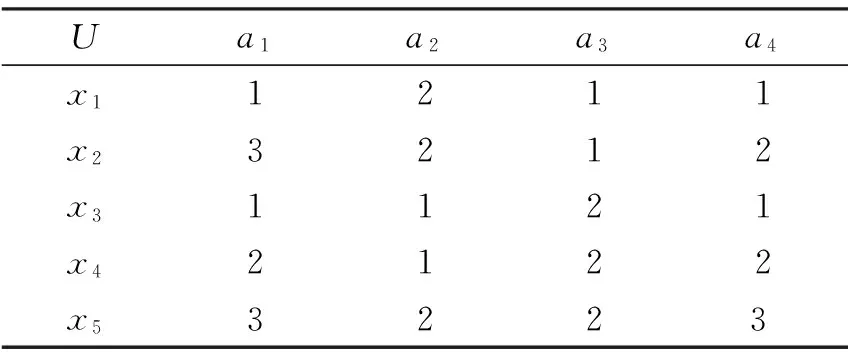
表1 序信息系统表

不妨取α=0.7。

然后计算AT与{ai}(i=1, 2, 3, 4)之间的α概率优势类结构差异度:

因为a1与a4下的概率优势类结构差异度最小且相等,不妨先取属性a1,此时概率优势类结构差异度不为0,于是进行下一步操作。

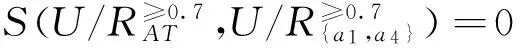
于是{a1, a4}为概率优势关系下的一个协调集,因为单个属性都不是协调集,所以{a1, a4}为约简。

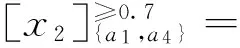
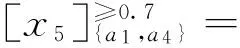
显然,{a1, a4}下的概率优势类与AT下的完全一样,即{a1, a4}为保持了该序信息系统概率优势类不变的约简,从而验证了该算法的正确性。

4 结 语

本文针对传统优势关系要求过于严格,以及已有概率优势关系定义的不完整性,提出一种更加合理的概率优势关系。进而研究了概率优势关系粗糙集模型的性质,提出概率优势类结构差异度的概念,并给出了一种该关系下属性约简的算法。此算法能有效地找到概率优势关系下序信息系统的一个约简。在序信息系统中,定义概率优势关系,并研究相关的性质和结论,在一定程度上丰富了序信息系统中知识获取和发现的理论。本文的后续将研究如何给出更简单的概率优势关系下属性约简算法,并进一步研究概率优势关系下不完备序信息系统中粗糙集的相关性质和属性约简问题。

[1] PAWLAK Z. Rough Sets[J]. International Journal of Computer and Information Science, 1982, 11(5): 341-356.

[2] PAWLAK Z. Rough Sets[J]. Communication of the ACM, 1995, 38(1): 89-95.

[3] 常犁云, 王国胤, 吴渝. 一种基于Rough Set理论的属性约简及规则提取方法[J]. 软件学报, 1999, 10(11): 1206-1211.

[4] 张文修, 梁怡, 吴伟志. 信息系统与知识发现[M]. 北京: 科学出版社, 2003.

[5] LINGRAS P J, YAO Y Y. Data mining using extensions of the rough set model [J]. Journal of the American Society for Information Science, 1998, 49(5): 415-422.

[6] LI M, DENG S B, WANG L, et al. Hierarchical Clustering Algorithm for Categorical Date Using a Probabilistic Rough Set Model[J]. Knowledge Based Systems, 2014, 65: 60-71.

[7] 王国胤, 张清华, 马希骜，等. 知识不确定问题的粒计算模型[J].软件学报, 2011, 22(4): 676-694.

[8] GRECO S, MATARAZZO B, SLOWINSKI R. Rough approximation of a preference relation by dominance relation[J].European Journal of Operation Research, 1999, 117: 63-83.

[9] GRECO S, MATARAZZO B, SLOWINSKI R. Rough Approximation by Dominance Relations[J].International Journal of Intelligent Systems, 2002, 17: 153-171.

[10] 徐伟华, 张文修. 基于优势关系下的协调近似空间[J]. 计算机科学, 2005, 32(9):164-165.

[11] SHAO M W, ZHANG W X. Dominance Relation and Rules in an Incomplete Ordered Information System[J]. International Journal of Intelligent Systems, 2005, 20(5):13-27.

[12] 桂现才.序信息系统属性约简的一种启发式算法[J].计算机工程与应用, 2008,44(27):168-171.

[13] 徐伟华, 张晓燕, 钟坚敏,等.序信息系统中属性约简的启发式算法[J]. 计算机工程, 2010, 36(17):69-71.

[14] XU W H, LI Y, LIAO X W. Approaches to attribute reductions based on rough set and matrix computation in inconsistent ordered information systems[J].Knowledge Based Systems, 2012, 27: 78-91.

[15] 吕跃进,韦碧鹏,胡明明.基于相对优势类差量的序信息系统属性约简算法[J].模糊系统与数学, 2013, 27(1):142-148.

[16] 孟慧丽, 赵晓焱, 徐久成. 序信息系统的贴近度及属性约简算法[J]. 计算机科学, 2014, 41(12):189-191.

[17] 翁世洲, 吕跃进. 基于概率优势关系的排序方法及应用[J]. 山西大学学报(自然科学版), 2015, 38(3):439-446.

[18] 徐伟华. 序信息系统与粗糙集[M]. 北京:科学出版社,2013.

(编 辑 亢小玉)

A rough set model and attribute reduction based on probabilistic dominance relation

SHI Yujie1, YANG Hongzhi2, WEI Ling3

(1.School of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, China;2.Henan University of Economics and Law, Zhengzhou 450046, China；3.School of Mathematics, Northwest University, Xi′an 710127， China)

For the ordered information systems, a modified definition of dominance relation is proposed and the relevant properties of rough set model based on probabilistic dominance relation are discussed firstly. Then a new definition of structure diversity on probabilistic dominance classes is proposed, following with a novel algorithm and some theories about attribute reduction. This study provides a new method to the theoretical basis of knowledge discovery in ordered information systems.

ordered information systems; probabilistic dominance relation; rough sets; attribution reduction

2015-11-01

国家自然科学基金资助项目(11371014)

施玉杰，女，河南周口人，从事形式概念分析、粗糙集理论研究。

O212；TP18

A

10.16152/j.cnki.xdxbzr.2016-05-005