含绝对值的不等式问题复习研究*
●王红权
(杭州市基础教育研究室 浙江杭州 310003)
含绝对值的不等式问题复习研究*
●王红权
(杭州市基础教育研究室 浙江杭州 310003)
含绝对值不等式的解法和三角形不等式的应用已写入《浙江省数学高考考纲》.为此需要对该内容作深入和系统地研究,纵观已有的真题,通过梳理知识结构,提取解题策略,破解命题轨迹,寻找复习灵感,实现新增内容从复习到考试的软着陆.
绝对值不等式;三角形不等式;复习研究;解题策略
2017年是浙江省数学高考文理不分卷考试的第1年,《浙江省2017年普通高等学校招生考试大纲·数学》(以下简称《大纲》)在第5章“不等式考试要求”中明确规定:5.会解|x+b|≤c,|x+b|≥c,|x-a|+|x-b|≥c,|x-a|+|x-b|≤c型不等式;6.了解不等式||a|-|b||≤|a+b|≤|a|+|b|(以下称该不等式为三角形不等式)及其应用.
《大纲》明确要求“会解”含有1个或2个绝对值的不等式,“了解”三角形不等式及其应用.历年浙江省和其他省市的数学高考中均有所涉及不等式内容,教师在复习时也会有所提及,但笔者认为系统梳理这类问题的解题方法仍是必要的.笔者通过举例给出这类问题的常用解题策略,供大家复习时参考.
1 含绝对值的不等式的解法研究
例1 解不等式|x-1|+|x-4|≥5.
(2013年浙江省数学高考自选模块试题)
分析1 (分类讨论法)对形如|x-a|+|x-b|≥c(或≤c)的不等式,一般均可利用分点a和b,分3种情况进行讨论(其中a,b,c∈R).
解法1 当x≤1时,原不等式可化为
(1-x)+(4-x)≥5,
解得x≤0;
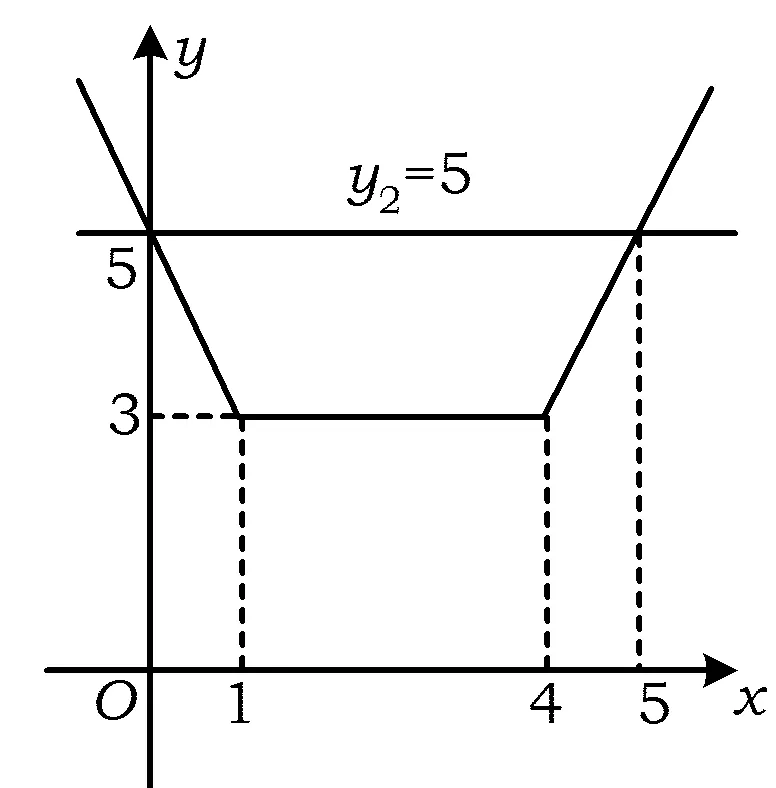
当1 (x-1)+(4-x)≥5, 得3≥5,此时x∈φ; 当x>4时,原不等式可化为 (x-1)+(x-4)≥5, 解得x≥5. 综上所述,该不等式的解集为(-∞,0]∪[5,+∞). 分析2 (几何法)利用不等式|x-a|+|x-b|≥c(其中c>0)的几何意义:解集是数轴上到点x1=a和x2=b的距离之和不小于c的集合.因为 |x-a|+|x-b|≥|(x-a)-(x-b)|=|a-b|, 所以当c≤|a-b|时,x∈R;当c>|a-b|且a 或 解法2 因为 |x-1|+|x-4|≥|(x-1)-(x-4)|=3, 所以由分析2知该不等式的解集为(-∞,0]∪[5,+∞). 分析3 (图像法)利用函数y1=|x-a|+|x-b|和y2=c的图像,数形结合求解. 图1 解法3 画出函数y1=|x-1|+|x-4|和y2=5的图像(如图1所示),观察图像,得不等式的解集为(-∞,0]∪[5,+∞). 评注 1)形如|x-a|+|x-b|≥c(或≤c)型的不等式主要有以上3种解法. 2)形如|x-a|+|x-b|≤c的不等式的解如下:当|b-a|>c时,x∈φ;当|b-a|≤c且a f(x)min=|b-a|. 4)推广:设f(x)=|x-a1|+|x-a2|+…+|x-an|(其中a1≤a2≤…≤an),若n为奇数,则 若n为偶数,则 例2 解不等式2|x-2|-|x+1|>3. (2014年浙江省数学高考自选模块试题) 分析1 (分类讨论法)与例1类似. 解法1 当x>2时,原不等式可化为 2(x-2)-(x+1)>3, 解得x>8; 当-1 2(2-x)-(x+1)>3, 解得x<0,此时-1 当x≤-1时,原不等式可化为 2(2-x)+(x+1)>3, 解得x<2,此时x≤-1. 综上所述,该不等式的解集为(-∞,0)∪(8,+∞). 分析2 (图像法)利用函数y1=k1|x-a|-k2|x-b|和y2=c的图像(其中k1,k2,a,b,c∈R),数形结合求解. 图2 解法2 画出函数y1=2|x-2|-|x+1|和y2=3的图像(如图2所示),观察图像,可知不等式的解集为(-∞,0)∪(8,+∞). 评注 1)形如|x-a|-|x-b|≥c(或≤c)型的不等式主要有2种解法. 图3 图4 2.1 在向量解题中的应用 当a,b是向量时,三角形不等式||a|-|b||≤|a±b|≤|a|+|b|仍成立.前一个等号成立的条件是向量a,b反向或至少有1个是零向量;后一个等号成立的条件是向量a,b同向或至少有1个是零向量. 例3 若非零向量a,b满足|a+b|=|b|,则 ( ) A.|2a|>|2a+b| B.|2a|<|2a+b| C.|2b|>|a+2b| D.|2b|<|a+2b| (2007年浙江省数学高考理科试题) 解 利用三角形不等式,得 |a+2b|=|(a+b)+b|≤|a+b|+|b|=|2b|. 因为a,b是非零向量,所以等号不成立.故选C. 例4 已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的取值范围是 ( ) (2013年湖南省数学高考理科试题) ||c|-|a+b||≤|c-a-b|=1, 从而 -1≤|c|-|a+b|≤1, 即 故选A. (2016年浙江省数学高考理科试题) 解 利用三角形不等式,得 |(a+b)·e|= |a·e+b·e|≤ 评注 1)向量形式的三角形不等式具有更为清晰的几何意义:三角形2边之和大于第3边,2边之差小于第3边. 2)利用三角形不等式解答向量模长取值范围的问题,简洁直观,很好地揭示了命题者的命题思路[1]. 3)三角形不等式刻画了向量空间的“平直”本质,是实现“向量空间代数化”的重要定理之一. 2.2 在函数解题中的应用 带有绝对值的函数最值问题,一般有2种处理方式:一是通过讨论去绝对值,化为常见函数求解;二是利用三角形不等式求解. 例6[2]若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是______. (2015年浙江省数学高考理科试题) 解 因为x2+y2≤1,所以 (3x+4y)2≤(32+42)(x2+y2)≤25, 即 |3x+4y|≤5. 设二元函数f(x,y)=|2x+y-2|+|6-x-3y|,则 f(x,y)≥ |(2x+y-2)-(6-x-3y)|= |3x+4y-8|≥8-|3x+4y|≥3, 例7 已知实数a,b,c,则 ( ) A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 B.若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100 C.若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100 D.若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100 (2016年浙江省数学高考理科试题) 解 由三角形不等式,得 |a2+b+c|+|a+b2-c|≤1, 从而 于是 即 同理可得 再利用三角形不等式,得 |2c+a2-a-b2+b|≤ |a2+b+c|+|a+b2-c|≤1, 即 |c|<3, 进而 故选D. 2)例7用三角形不等式估计的上界改进了答案给出的上界,笔者认为命题者给出的上界“100”既满足了考试的选拔要求,又比较人性化. 例8 已知f(x)=ax2+bx+c,g(x)=cx2+bx+a,对任意x∈[-1,1],都有|f(x)|≤1,设h(x)=|f(x)|·|g(x)|,证明:h(x)≤2. 证明 由题意,知 f(1)=a+b+c,f(0)=c,f(-1)=a-b+c, 且 |f(1)|≤1, |f(0)|≤1, |f(-1)|≤1, 解得 从而 于是 h(x)=|f(x)|·|g(x)|≤2, 其中f(x)=2x2-1满足条件. 例9 已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b(其中x∈[0,1]),证明:|f(x)|≤|2a-b|+a. (2012年浙江省数学高考理科试题改编) 引理1 若0≤x≤1,则 |2x3-3x+1|+|2x3-x|≤1. 引理1的证明 根据平凡恒等式|a|+|b|=max{|a+b|,|a-b|},知 |2x3-3x+1|+ |2x3-x|= max{|4x3-4x+1|,|1-2x|}. 当0≤x≤1时,|1-2x|≤1显然成立.因为4x3-4x+1≤1⟺x(x2-1)≤0,所以4x3-4x+1≤1显然成立.又因为4x3-4x+1≥-1⟺x(2-2x)(1+x)≤1,根据三元均值不等式,得 所以4x3-4x+1≥-1也成立. 综上所述,|2x3-3x+1|+|2x3-x|≤1. 例9的证明 因为f(0)=-a+b,f(1)=3a-b,所以 又f(0)+f(1)=2a>0,从而 max{|f(0)|,|f(1)|}=max{f(0),f(1)}, 于是|f(x)|= |(2x3-3x+1)·f(0)+(2x3-x)·f(1)|≤|2x3-3x+1|·|f(0)|+|(2x3-x)|·|f(1)|≤max{|f(0)|,|f(1)|}·(|2x3-3x+1|+|2x3-x|)≤max{|f(0)|,|f(1)|}=max{f(0),f(1)}= 评注 这里使用了平凡恒等式:若a,b是实数,则 例10 函数f(x)=4x3+ax2+bx+c满足:当|x|≤1时,|f(x)|≤1,求实数a,b,c的值. (2012年天津市高中数学联赛预赛试题) |4+a+b+c|≤1, (1) |-4+a-b+c|≤1, (2) (3) (4) 由式(1)和式(2)得 |8+2b|= |(4+a+b+c)-(-4+a-b+c)|≤ |4+a+b+c|+|-4+a-b+c|≤2, 从而 |4+b|≤1. (5) 从而 |1+b|≤2. (6) 由式(5)和式(6)解得b=-3.此时,由式(1)和式(2)得a+c=0,由式(3)和式(4)得 解得a=c=0,故 f(x)=4x3-3x, 易证该函数满足条件. 评注 1)在例8和例9中,利用函数值的有界性,用函数值表达系数,代换后用三角形不等式放缩,获得函数值的界,是一种简单有效的方法,初学者容易掌握.例9的解答则是完全初等的,改编后的试题浑然一体. 2)例10的解法非常巧妙,通过对函数赋值,获得部分系数组合的取值范围,利用问题成立的必要性,缩小范围,然后再验证其充分性.这种解法简洁灵巧,但需要解题者有较强的数学洞察力(直觉),是体现学生数学核心素养的好题. 2.3 在不等式证明中的应用 在高等数学中,利用三角形不等式进行放缩是常见的也是基本的方法. (2016年江苏省数学高考试题) 证明 因为 |2x+y-4|=|2(x-1)+(y-2)|≤ |2(x-1)|+|(y-2)|< 所以 |2x+y-4| 待证不等式成立. 当k=2时, 待证不等式成立. 例13 设y=f(x)是定义在区间[-1,1]上的函数,且满足条件:1)f(-1)=f(1)=f(0);2)对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|,证明:|f(u)-f(v)|≤1. (2003年北京市数学高考试题改编) 证明 因为u,v∈[-1,1],当|u-v|≤1时, |f(u)-f(v)|≤|u-v|≤1; 当|u-v|>1时,则uv<0.不妨设u<0,v>0,则v-u>1,因为f(-1)=f(1)=f(0),所以 |f(u)-f(v)|= |f(u)-f(-1)-f(v)+f(1)|≤ |f(u)-f(-1)|+|f(v)-f(1)|≤ |u+1|+|v-1|=1+u+1-v= 2-(v-u)<1. 综上可知,对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1. 评注 1)证明条件为绝对值不等式,结论为含有绝对值的不等式的最佳“武器”是三角形不等式. 2)例10和例11的放缩方法在高等数学中很常见,在中学和大学数学的衔接处命题,彰显命题者的立意,例12中插入2个等值点f(-1)和f(1)的做法在高等数学中也是常见的技巧. 3)由此可见,命题者常常用自己熟悉的内容为切入点进行命题. 2.4 在数列中的应用 (2016年浙江省数学高考试题改编) 证明 由三角形不等式,得 从而 整理即得 |an|≥2n-1(|a1|-2). 三角形不等式和解绝对值不等式综合应用,含有2个绝对值的函数的性质及应用,也常见于某些大型的考试中,这方面的问题在复习中也值得重视. 例15 不等式|2x-a|+|3x-2a|≥a2,对任意x∈R恒成立,则满足条件的实数a组成的集合为 ( ) (2016年中国科学技术大学自主招生试题) 解 设f(x)=|2x-a|+|3x-2a|≤ 例16 若f(x)=(x+a)(|x-a|+|x-4|)的图像是中心对称图形,则a=______. (2014年浙江省嘉兴市数学一模考试试题) 要使函数f(x)的图像是中心对称图像,则经过适当平移后,函数f(x+t)为奇函数即可,因此只需要函数g(x+t)=|x+t-a|+|x+t-4|为偶函数,函数h(x+t)=(x+t+a)为奇函数,从而 解得 评注 1)任何图像成中心对称的函数总能通过平移,使得函数变为奇函数. 2)任何图像成轴对称的函数总能通过平移,使得函数变为偶函数. 2017年数学高考文理科合卷,复习教学时必须把握好教学的难易,需要落实基本概念,强化基本运算,需要落实数学基本方法,培养数学直观.“学会用数学眼光观察世界,用数学思维分析世界,用数学语言表达世界”. [1] 王红权.一类与向量模长有关试题的简洁解法[J].中国数学教育,2015(3):35-38. [2] 数学高考研究组.浙江高考数学2004一路走来[M].杭州:浙江大学出版社,2016. [3] 王红权.最值互嵌问题的解题策略[J].中学教研(数学),2016(6):12-15. �2016-08-14; 2016-09-20 王红权(1970-),男,浙江杭州人,中学高级教师.研究方向:数学教育. O122.3 A 1003-6407(2016)12-29-06

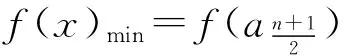


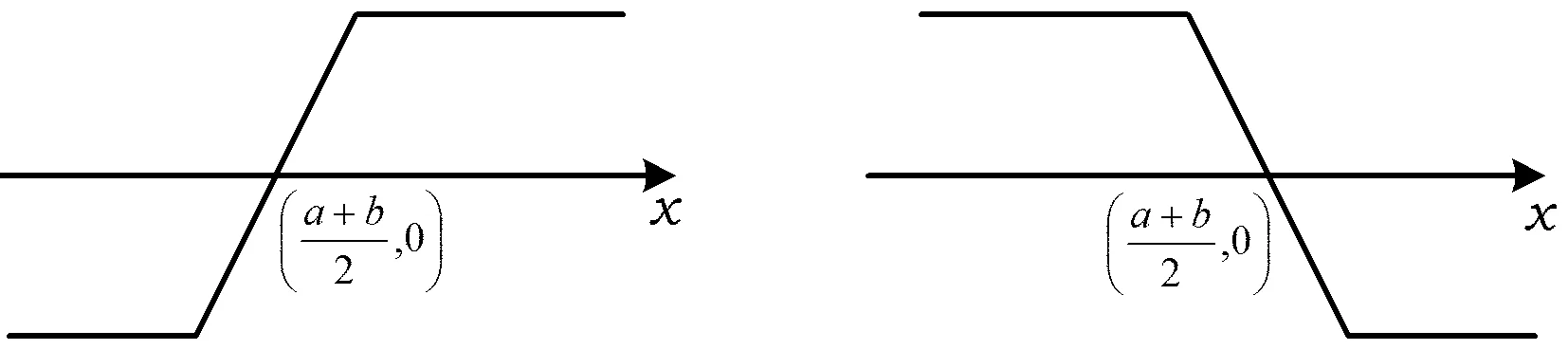
2 三角形不等式应用研究

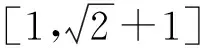
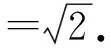





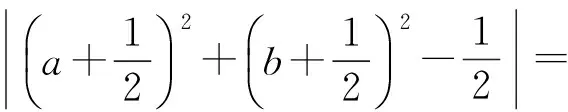

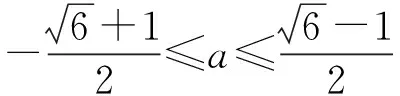
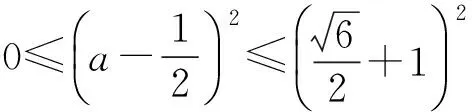

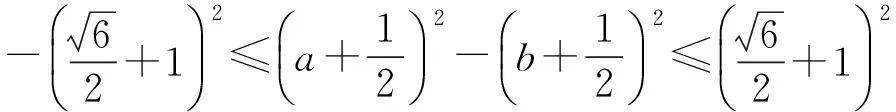
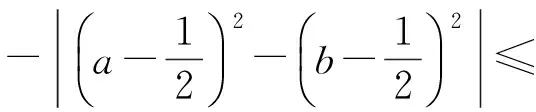

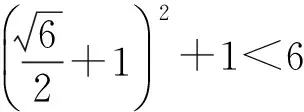


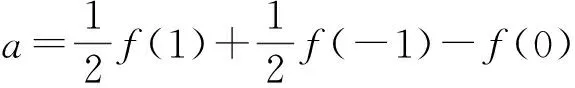


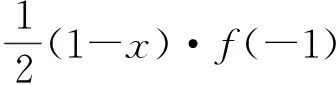
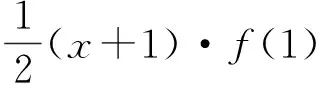

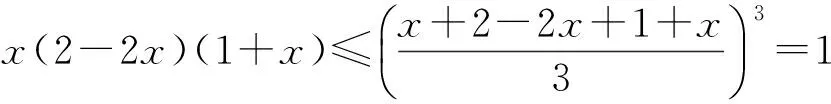

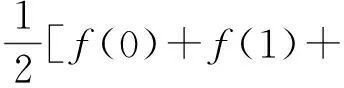
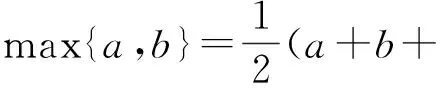
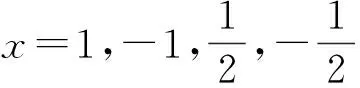

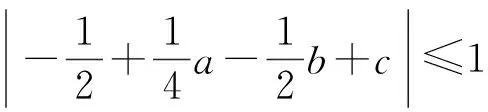
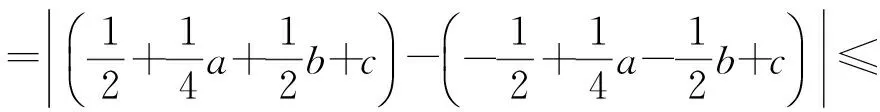


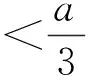


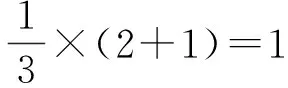

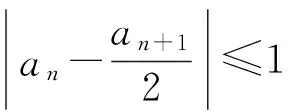
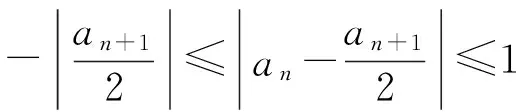
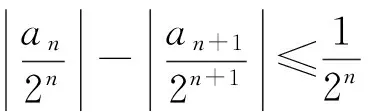

3 相关应用