基于灵敏度分析的桁架结构动力学尺寸优化
周奇才,吴青龙,陈明阳,熊肖磊
(同济大学 机械与能源工程学院,上海 201804)
基于灵敏度分析的桁架结构动力学尺寸优化
周奇才,吴青龙,陈明阳,熊肖磊
(同济大学 机械与能源工程学院,上海 201804)
以桁架结构杆件截面尺寸参数为设计变量,以结构重量为目标函数,以结构的固有频率为约束条件,建立桁架结构的动力学尺寸优化设计数学模型.通过推导固有频率和结构重量对杆件截面尺寸的灵敏度,确定优化杆件及优化步长,建立了结构尺寸优化设计方法并制定了在ANSYS软件中的实现方案.方法能有效地改变结构固有频率,避免处于动载荷作用下的结构因发生共振而破坏.最后,使用数值算例验证了优化方法的有效性.
桁架; 尺寸优化; 固有频率; 灵敏度; 动力学
在结构优化设计领域,静力学优化方法已十分成熟,包括结构拓扑、形状、尺寸优化设计方法.但工程中的结构,不可避免地会受到风激、地震、波浪或者货物的突然加载和卸载等振动和冲击载荷的作用.而随工程技术的进步,对结构性能的要求也越来越高,结构不仅要满足静力学强度、刚度和稳定性要求,还要满足动力学性能的要求.因此,结构动力学优化设计逐步发展起来.结构动力学优化是一门集有限单元法、结构动力学、数学优化算法、数值计算方法以及程序设计等多学科于一体的学科,是现代工程领域较为复杂的研究分支[1-2].考虑结构优化设计变量与结构外形的关系,动力优化设计与结构静力优化一样可分为动力尺寸优化、形状优化[3]和拓扑优化[4].考虑优化设计对结构性能的影响,动力优化设计可分为结构动力特性的优化设计[5]和结构响应的优化设计[6].结构动力特性优化设计是指对结构的固有频率、振型、阻尼、重量与刚度等进行优化; 结构动力响应优化设计是以动载荷激励下结构的响应为目标或约束的优化设计.
本文以桁架结构杆件截面尺寸参数为设计变量,以结构重量为目标函数,以结构的固有频率为约束条件,建立了桁架结构的动力学尺寸优化设计数学模型,推导了目标函数和约束条件对设计变量灵敏度的表达式,找到了固有频率灵敏度与重量灵敏度比值大的杆件并以此确定优化方向.以结构刚度矩阵的变化量确定优化步长并实现了桁架结构频率约束下的尺寸优化设计.
1 优化数学模型
桁架结构动力学尺寸优化设计的数学模型可描述如下:
(1)
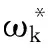
2 灵敏度分析
2.1 固有频率灵敏度
无阻尼结构的振动特性可由特征方程(2)给出:
(2)
方程(2)本质上是一个广义特征值问题.其中,K,M 分别为结构的总体刚度矩阵和总体质量矩阵,方程的特征值λk=ωk2,特征值λk对应的特征向量Xk为固有频率ωk下的结构振型向量.
为求固有频率ωk对杆件截面尺寸参数ai的灵敏度,式(2)两端对设计变量ai微分可得:
(3)
式(3)两端左乘XkT,并整理得到:
(4)
式(2)两边进行转置运算可以得到XkTKT=λkXkT·MT,因刚度矩阵和质量矩阵K,M为对称矩阵,故有:
(5)
因此式(4)可化为
(6)
整理式(6)即可得到特征值的灵敏度:
(7)
式(2)两边乘以XkT可以得到式(8).
XkTKXk=λkXkTMXk
(8)
假设XkTMXk=δk,则XkTKXk=λkδk.将振型Xk对质量矩阵归一化,假设Xk1=αXk为归一化后的振型,则有:
(9)
振型归一化后,式(7)可转化为
(10)
(11)
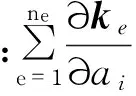
空间桁架的有限元法中,杆单元在单元坐标系下的刚度矩阵和一致质量矩阵可表示如下:
(12)
(13)
要由单元坐标系下的刚度矩阵和质量矩阵组集总体刚度和质量矩阵,需要将单元刚度矩阵、质量矩阵转换到全局坐标系下,其坐标变换矩阵如下:
(14)
α为单元坐标系与全局坐标系之间的夹角.
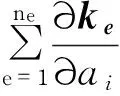
(15)
(16)
(17)
(18)
将式(17),(18)代入(11),式(11)可转化为
(19)
式(19)即为无阻尼桁架结构固有频率对桁架中杆件截面尺寸参数的灵敏度.
2.2 重量灵敏度
桁架结构中,重量对桁架截面积设计变量的灵敏度较为简单,如式(20)所示.
(20)
2.3 单元灵敏度
为表征结构的优化效率,引入单元灵敏度的概念,如式(21)所示.它表示了改变杆单元i的截面积所带来的结构频率收益Δω2与结构重量支出ΔM的比值,该比值越大则表明此杆单元的优化效率越高,在优化时优先改变这些杆件的截面积.
(21)
3 优化设计方案
单元灵敏度si的大小表示了设计变量的优化效率.si越大则增大杆件i的截面积所带来的频率改变量越大.为平衡优化效果与计算量,需确定每次优化迭代中对哪些杆件的截面参数进行调整及调整的幅度,具体的优化方案如下.
3.1 设计变量移动方案
假定si>1的单元为有效优化单元,为增强优化效果,每次迭代中选取有效优化单元中灵敏度最大的50%作为移动单元,改变这些单元的截面尺寸.
3.2 移动步长
尺寸的移动步长是一个重要的优化控制参数,移动步长小,则优化过程更为精确,但优化进程则较为缓慢,计算成本增加.而过大的移动步长可能导致优化设计收敛困难.在移动中,要求保证总体刚度矩阵的变化量ΔK相对于总体刚度矩阵K在一个很小的量级内,如2%K—5%K,在文中取5%.因总体刚度矩阵和总体质量矩阵都是带状稀疏矩阵,可采用矩阵的迹来近似代表矩阵[7].即有:
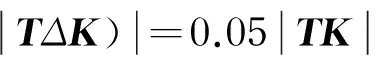
(22)
在单元层次上可表示为
(23)
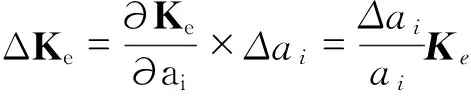
3.3 优化终止条件
如数学模型式(1)中所示,当结构固有频率满足约束条件,且各杆件截面积在约束范围内,则优化完成,终止条件如式(24)所示.
(24)
4 ANSYS软件中的优化流程
在ANSYS软件中实现桁架结构固有频率优化的重点在于固有频率灵敏度的计算,其中涉及到刚度矩阵、质量矩阵的提取与组装,以及刚度矩阵、质量矩阵、频率、振型之间的向量与矩阵运算等[8-10].具体流程如图1所示.
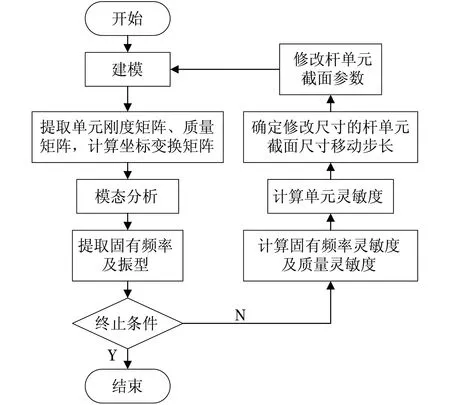
图1 ANSYS中优化流程图
5 数值算例
5.1 问题描述
以如图2所示的平面桁架结构为例对算法进行验证.桁架结构中杆件材料为铝,弹性模量E=68.97GPa,密度ρ=2 768kg·m-3.结构中各节点的坐标及各杆件尺寸参数如表1所示.假设因工程实际需求,该桁架结构的基频需大于20Hz,各杆件截面的最小尺寸为6.45cm2,最大尺寸为225.81cm2.求满足该条件的最小重量桁架.该优化问题可用数学模型(25)描述.
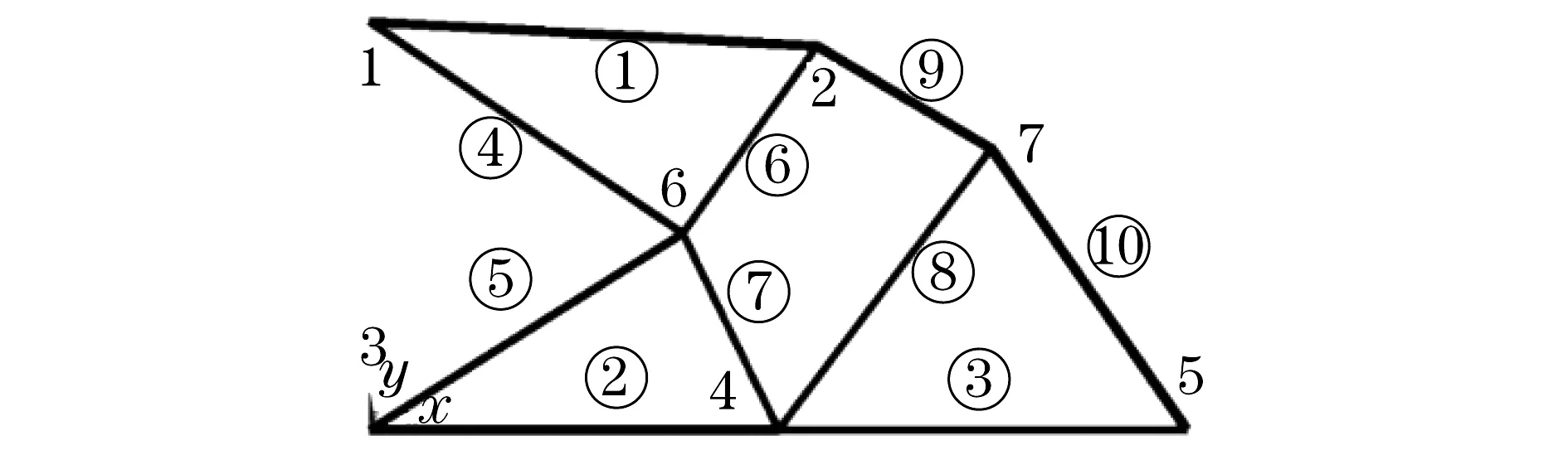
图2 优化算例桁架示意图
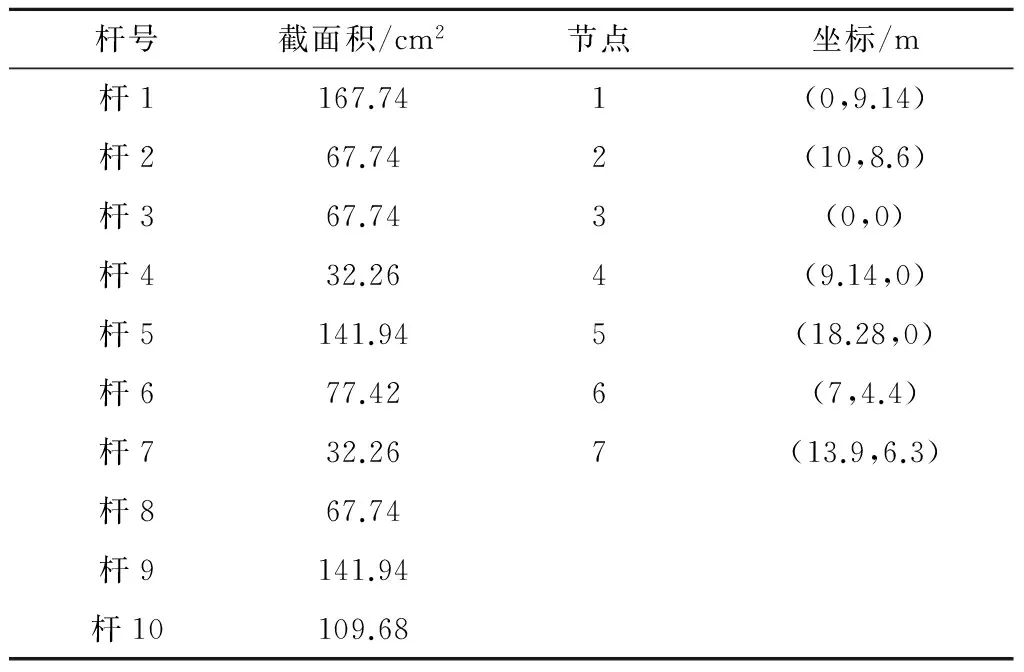
杆号截面积/cm2节点坐标/m杆1167.741(0,9.14)杆267.742(10,8.6)杆367.743(0,0)杆432.264(9.14,0)杆5141.945(18.28,0)杆677.426(7,4.4)杆732.267(13.9,6.3)杆867.74杆9141.94杆10109.68
(25)
5.2 优化结果
如图3所示为优化过程中结构基频和重量的变化图线.
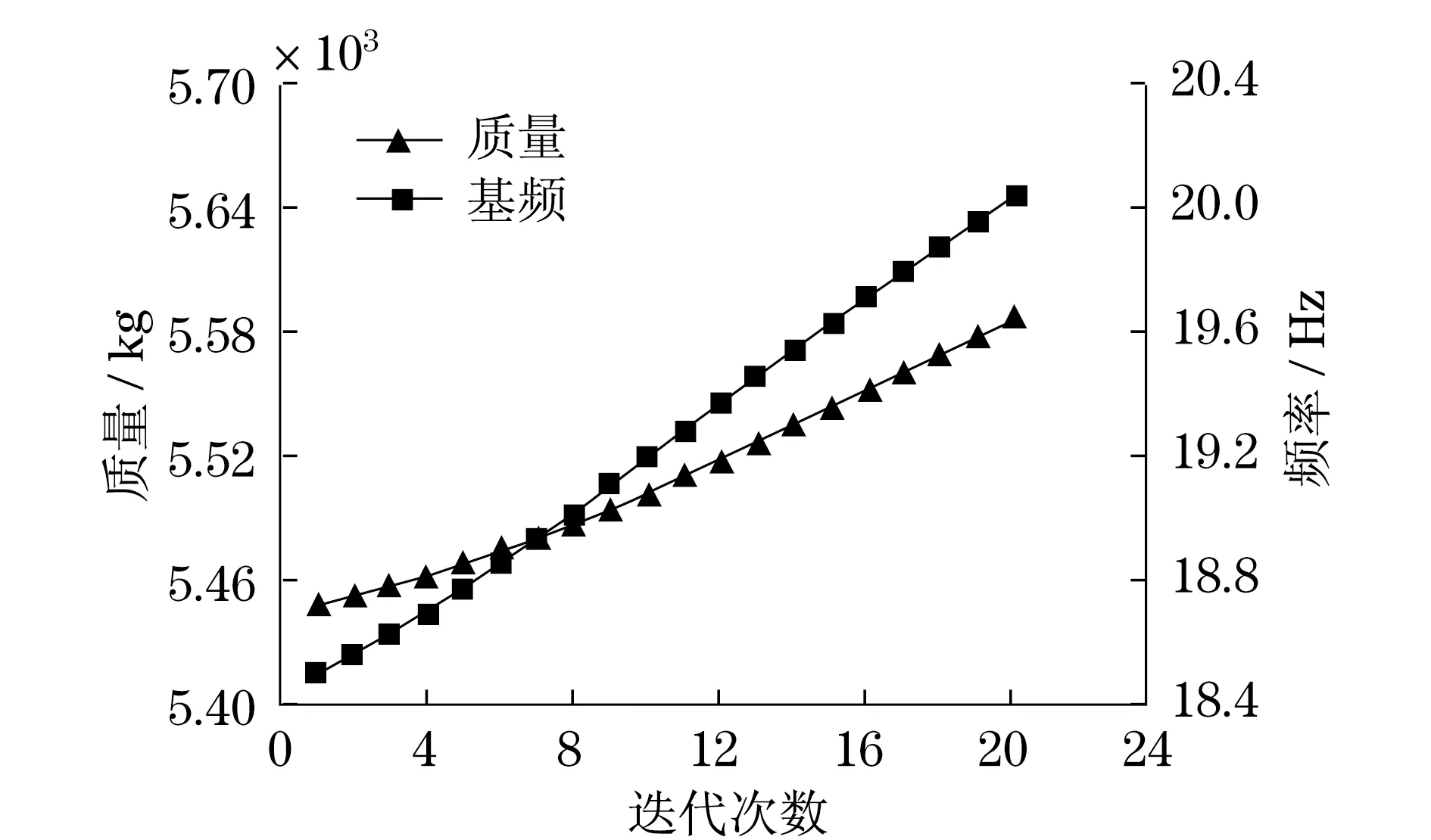
图3 桁架基频和重量的优化过程数据
结构优化前后的固有频率及重量数据如表2所示.
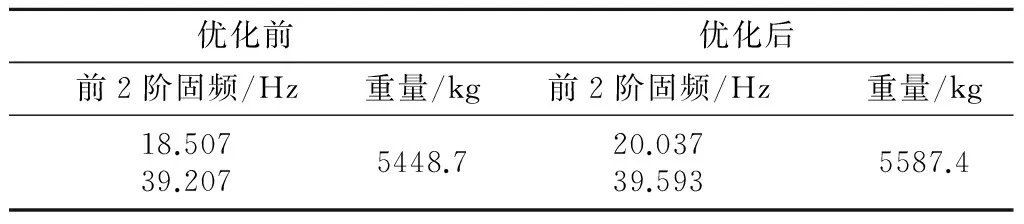
表2 桁架优化前后的固有频率和重量对比数据
优化后结构的杆件截面尺寸数据如表3所示.
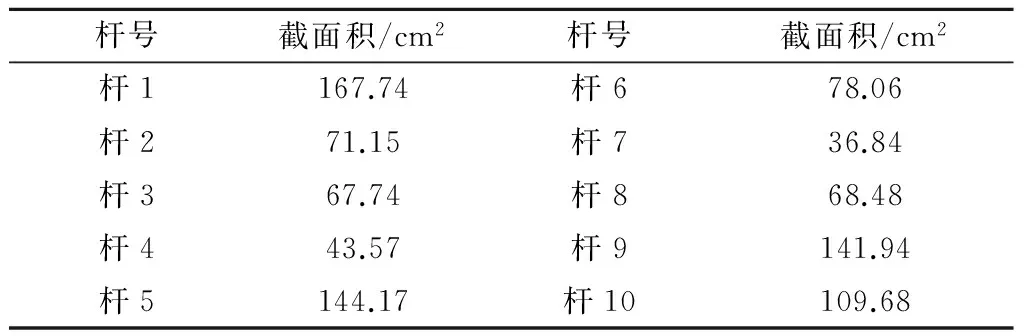
表3 桁架优化后杆件的截面积参数
由上述数据可知,优化后结构的第一阶固有频率增加了8.27%,结构重量增加了2.54%.以较小的重量代价获得了较大的固有频率收益.
6 结论与讨论
文章建立了桁架结构动力学尺寸优化设计的数学模型,推导了结构固有频率和重量的灵敏度表达式,确定了设计变量的优化方案,并用数值算例验证了算法的有效性.该优化设计方法的意义在于,通过固有频率的约束,可使结构避开其工作环境中动载荷的激励频率,从而避免结构因发生共振而破坏.基于灵敏度分析对桁架结构进行优化,由于利用了结构固有频率和重量对设计变量的导数信息,故具有较高的优化效率和较好的优化效果.
[1] 陈建军,车建文,崔明涛,等.结构动力优化设计述评与展望[J].力学进展,2001(2):181-192.
CHENJianjun,CHEJianwen,CUIMingtao,etal.Reviewandoutlookofstructuraldynamicoptimizationdesign[J].AdvancesinMechanics,2001(2):181-192.
[2] 顾松年,徐斌,荣见华,等.结构动力学设计优化方法的新进展[J].机械强度,2005(2):156-162.
GUSongnian,XUBin,RONGJianhua,etal.Recentprogressesonstructuraldynamicdesignmethods[J].JournalofMechanicalStrength,2005(2):156-162.
[3] 薛运虎,韦凌云,赵玫,等.基于演化算法的带频率约束的桁架结构形状和尺寸优化[J].振动与冲击,2010(12):13-17.
XUEYunhu,WEILingyun,ZHAOMei,et.al.Trussshapeandsizeoptimizationwithfrequencyconstraintsbasedonevolutionaryalgorithm[J].JournalofVibrationandShock.2010(12):13-17.
[4]XUB,JIANGJ,TONGW,etal.Topologygroupconceptfortrusstopologyoptimizationwithfrequencyconstraints[J].JournalofSoundandVibration.2003,261(5):911-925.
[5]GRANDHIR.Structuraloptimizationwithfrequencyconstraints-areview[J].AIAAJournal,1993,31(12):2296-2303.
[6] 肖方豪.结构动力响应优化和结构动力鲁棒设计研究[D].重庆:重庆大学,2007.
XIAOFanghao.Dynamicresponseoptimizationofstructuresandrobustoptimaldesigninstructuraldynamics[D].Chongqing:ChongqingUniversity,2007.
[7] 李艳辉.刚架结构动力学形状优化[D].西安:西北工业大学,2005.
LIYanhui.Frameshapeoptimizationsubjecttodynamicsconstraints[D].Xi′an:Northwestern Polytechnical University,2005.
[8] 张锦江.多阶频率与振型约束下的结构动力学优化设计[D].西安:西北工业大学,2007.
ZHANG Jingjiang.Structural dynamics optimization design with constraints of multiple natural frequencies and modal shapes[D].Xi′an:Northwestern Polytechnical University,2007.
[9] 龚曙光,谢桂兰,黄青云.ANSYS参数化编程与命令手册[M].北京:机械工业出版社,2009.
GONG Shuguang,XIE Guilan,HUANG Qingyun.ANSYS parametric programming and command manual[M].Beijing:China Machine Press,2009.
[10] WANG D,ZHANG W H.Truss optimization on shape and sizing with frequency constraints[J].AIAA J,2004,42(3):622-630.
Dynamic size optimization of truss based on sensitivity analysis
ZHOU Qi-cai,WU Qing-long,CHEN Ming-yang,XIONG Xiao-lei
(School of Mechanical Engineering,Tongji University,Shanghai 201804,China)
Using the section size as design variable,truss weight of truss as objective and natural frequency as constraints,the mathematical model for dynamics size optimization design of truss structure is established.Based on the mathematical model,the sensitivity of natural frequency and structural weight to section size is deduced and thus the members to optimize and their optimization step length is determined.These make up the truss size optimization method,which is then accomplished in the ANSYS software.The method can prevent structures from resonance breakage by adjusting the natural frequency efficiently.Finally this truss size optimization method is illustrate by an example.
truss; size optimization; natural frequency; sensitivity; dynamics
周奇才(1962-),男,教授,博士生导师.E-mail:Qczhou@tongji.edu.cn
TH11
A
1672-5581(2016)03-0254-05

