基于非奇异快速终端滑模的非线性轮胎力控制研究

仝 光,王 强

(上海电机学院汽车学院，上海 201306)



基于非奇异快速终端滑模的非线性轮胎力控制研究

仝 光,王 强

(上海电机学院汽车学院，上海 201306)

针对分层式集成控制系统在不同路面工况下车辆纵向力的控制问题,提出了一种基于模型的实时估计方法.首先选取魔术公式作为参考轮胎模型,并采用有约束混合遗传算法对其关键参数进行实时优化辨识,从而可以计算得到不同路面工况下与目标控制力对应的目标控制滑移率.采用非奇异快速终端滑摸控制方法(Nonsing ular Fast Terminal Sliding Mode,NFTSM)设计纵向滑移率控制器(Longitudingl Slip ratio Control,LSC)对目标滑移率进行跟踪控制.仿真结果表明:所提出的轮胎-地面力控制策略可以很好地跟踪不同路面工况下的滑移率,满足上层控制所需的目标控制力,从而对车辆进行优化控制.

参数辨识; 轮胎力控制; 约束混合遗传算法; 非奇异快速终端滑模控制

为了提高复杂工况下车辆的安全性、舒适性,现代车辆载有各种主动安全系统(ABS,4WS,ESP等).但同时暴露出来的问题是这些子系统之间的冲突和协调问题,因此集成控制已成为一个研究热点[1-5].

当然这些研究的确提高了车辆的性能,但大多集中在研究所需目标力或力矩的获取之上,而对具体的轮胎-地面力的执行的研究却比较少,有的也只是采取一些相对比较简单地分配、执行方式,例如,将所需的横摆力矩采用车差速制动的方式简单的分配在同一车轴的两边车轮上[3].针对这个问题,已经有学者对其进行了不同程度的研究[6].然而车辆的路面运行工况是不断变化的,因此,轮胎-地面力的自调节控制需要进一步的研究.为了进一步提高伺服系统对复杂多变路况的适应性,本文对轮胎力的实时辨识及自调节控制进行研究.

1 轮胎模型

这里选取魔术公式作为参考轮胎模型,在定载荷工况下,轮胎的纵向摩擦系数描述如下:

(1)

式中:μL纵向力摩擦系数;μ为纵向力地面摩擦系数函数;λ纵向滑移率;BL刚度因子;CL形状因子;DL峰值因子;EL曲率因子.事实上,车辆的运行工况是复杂多变的,例如不断变化的路面工况.因此,魔术公式的关键参数BL,CL,DL和EL需要实时估计,详情参见第3节.

2 自调节轮胎力控制结构设计

自调节轮胎力控制系统是主/伺服环底盘集成控制系统的子执行系统,如图1所示.主环系统计算提高车辆安全性、稳定性所需的理想力或力矩,并最优地分配在各个执行子系统中.伺服环系统具体实现上层所分配的最优力或力矩,例如轮胎地面力、主动车轮转角.这里主要关注的是纵向轮胎-地面力的跟踪控制.自调节轮胎力控制系统主要分为以下两个步骤:

步骤1:计算与主环系统提供的目标纵向轮胎-地面力对应的滑移率.首先采用有约束混合遗传算法对时变路面下魔术公式的关键参数进行最优辨识,得到不同路面工况下的轮胎力动力学特性.然后采用数值方法,计算得到与目标控制力对应的目标滑移率,这将是自调节轮胎力控制系统的控制目标.

步骤2:用所设计的滑移率控制系统LSC对目标滑移率进行跟踪控制,实现整车集成控制系统的最终控制目标.LSC系统控制算法采用非奇异快速终端滑模方法.

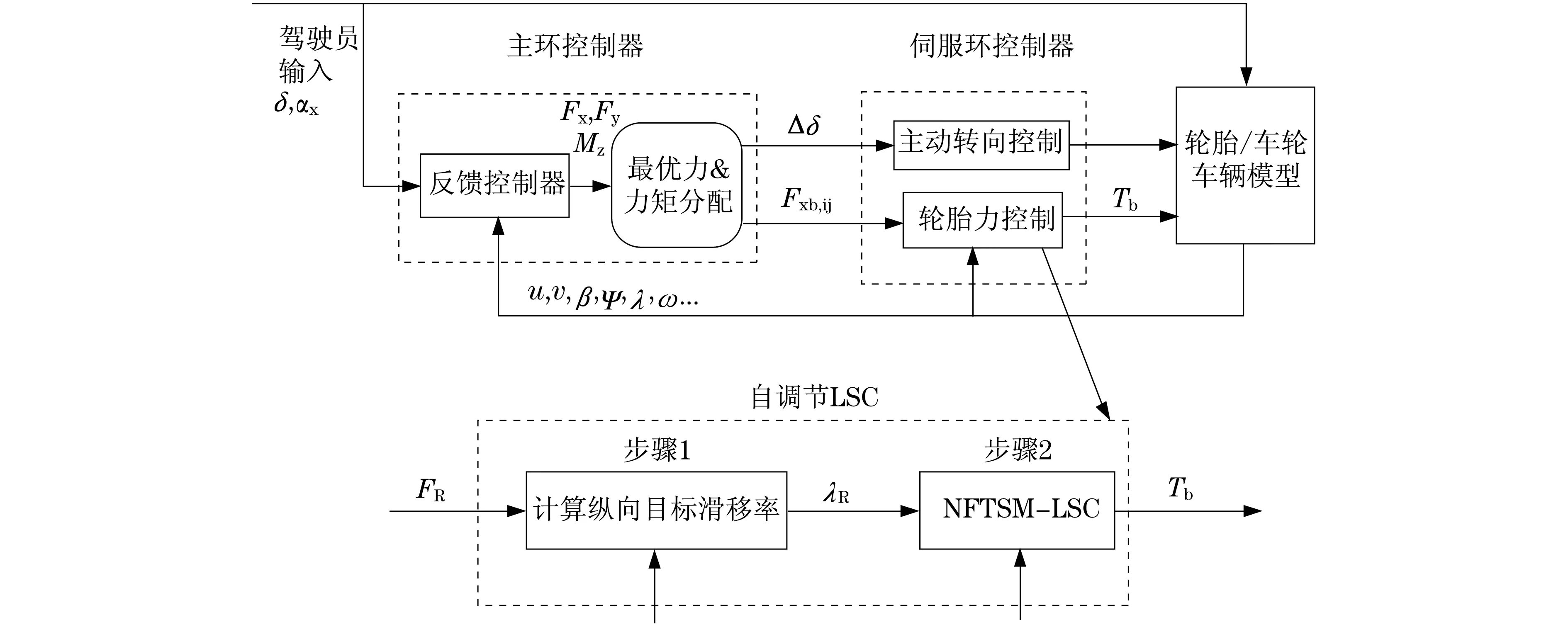
图1 主/伺服环集成系统及自调节轮胎力系统的结构图

3 参考轮胎模型参数优化辨识及目标纵向滑移率的计算

纵向轮胎-地面摩擦力估计是自调节轮胎力控制系统的先决条件.对于装有轮毂电机的电动汽车来讲,制动/驱动力矩可以通过点击自身的传感信息获取,因此可以方便地对轮胎力进行估计.而对于传统的ABS(Anti-locked Brake Sysem)系统,不能直接得到这些信息,因此难以对轮胎力进行更为有效的估计.为此,已有学者对传统的ABS系统进行了进一步的研究,使得其有与轮毂电机类似的功能,在制动钳上增加力传感器是其中一个简便有效的方法[7].基于这种方法,轮胎-地面力的估计算法具体如下.

首先简单介绍一下四分之一车辆模型,如图2所示.其动力学运动方程如下:

(2)

(3)

FZ=mg

(4)

式中:m为四分之一车辆质量;u为车辆纵向速度;Fxb为轮胎-地面力;J为车轮转动惯量;ω为车轮角速度;rb为车轮半径;Tb为制动力矩;FZ为垂向载荷;g为重力加速度.

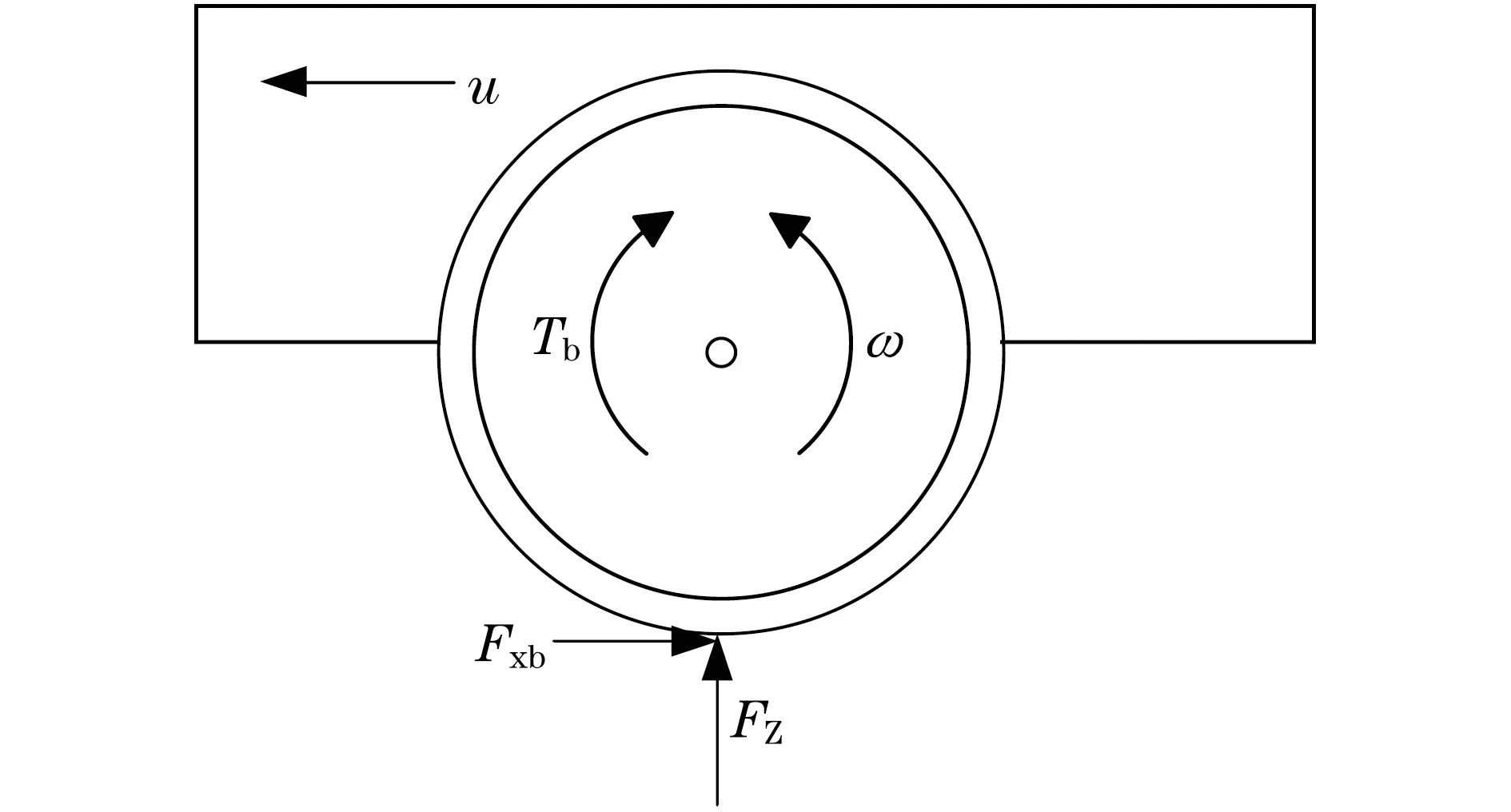
图2 四分之一车辆模型

则轮胎力估计方程如下:

(5)

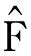
(6)

轮胎-地面摩擦力Fxb与滑移率λxb的非线性动力学方程如下:

(7)

式中μxb是摩擦系数.

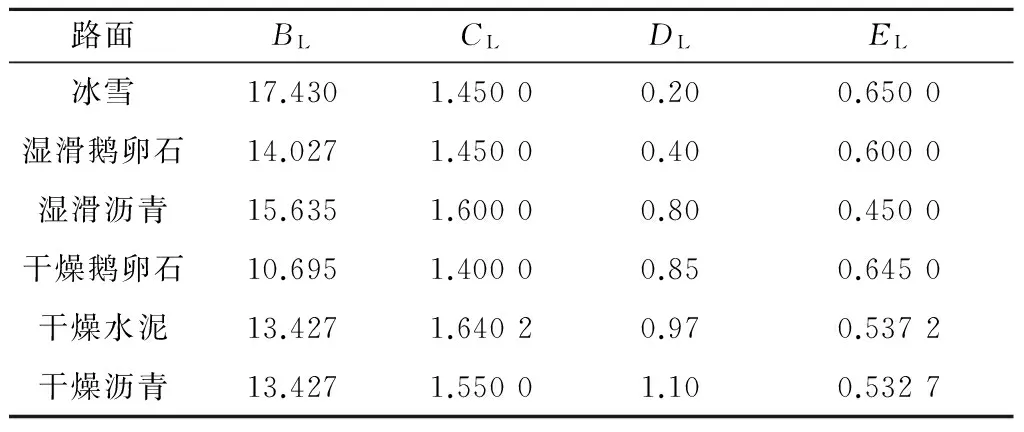
为了更为精确地估计魔术公式的关键参数BL,CL,DL和EL,使其与原始值之间的误差最小.首先建立优化目标函数,这里选取估计值与参考值(原始值)之间差的平方的加权函数作为优化目标函数PI.同时,考虑到各种路面工况下,轮胎-地面摩擦力的摩擦椭圆约束特性,优化目标函数的优化范围也被限定在此之内.这样,参考模型参数最优化辨识问题就被转化为一个有约束优化问题,具体描述如下:

(8)

(9)

其中wi是权重因子,xmin和xmax分别是魔术公式关键参数BL,CL,DL和EL的约束下下边界.

遗传算法(Generic Algorithm,GA)是应用很广泛的优化算法之一,但是它具有随机性.主动集二次规划算法(Sequential Quadratic Programming,SQP)可以很好地处理优化问题,但是初始值对其运算有很大影响,因此,PI极小值的优化算法选取的是兼顾这两种算法优点的有约束混合算法.

实时获得车轮运行路况的轮胎参数后,与主环系统所得到的目标纵向力FR所对应的滑移率λR通过求解下面非线性方程就可获取:

(10)

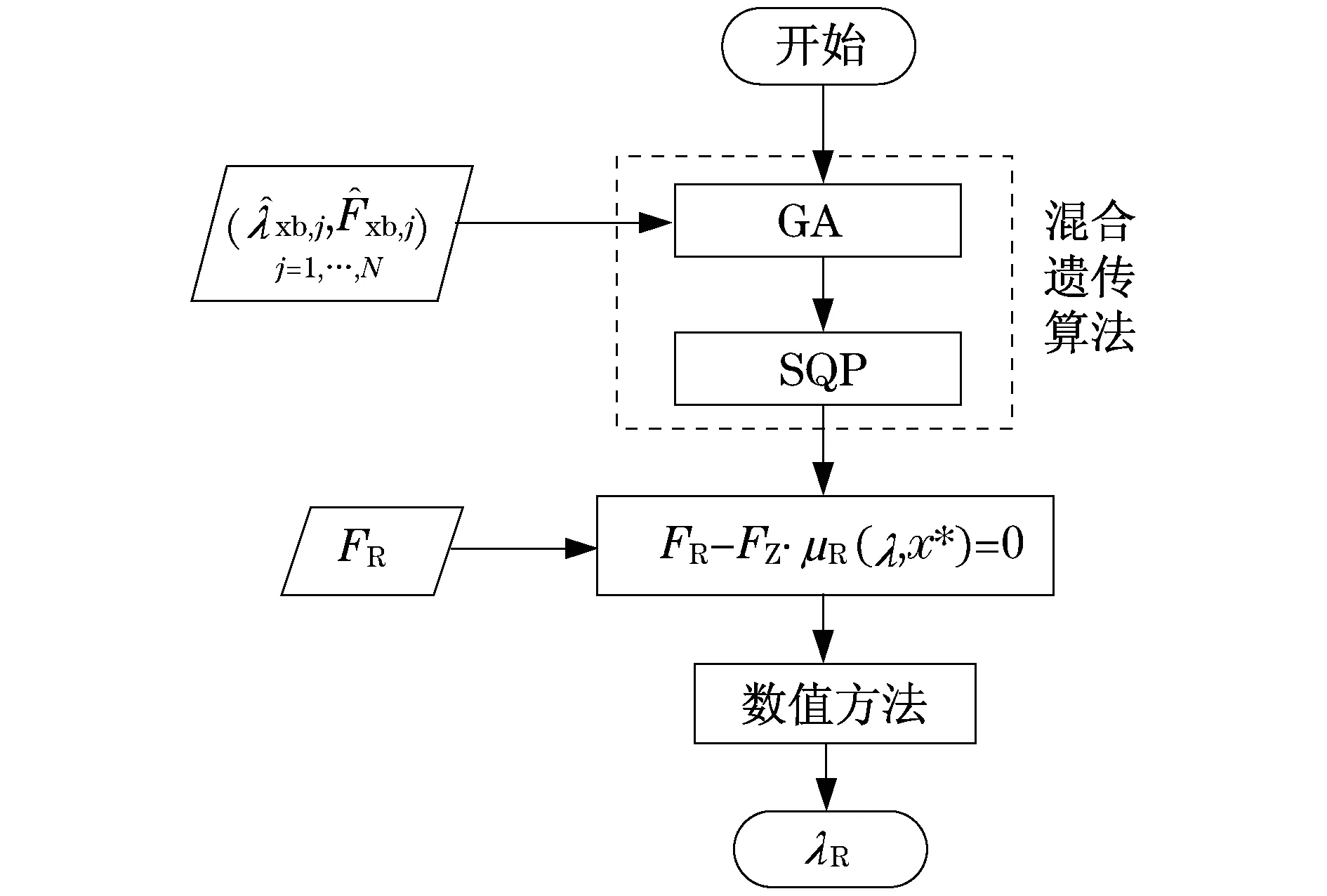
图3 计算目标滑移率流程图

4 基于NFTSM的LSC控制器设计

滑模变结构控制由于对模型误差和|外部干扰具有较好的鲁棒性,在不确定非线性系统的控制中得到了广泛应用.终端滑模(Teminal Sliding Mode,TSM) 的控制系统因具有有限时间收敛的优点,故其成为现代控制的一个研究热点.但是终端滑膜控制在远离平衡点时的收敛速度会变慢.非奇异终端滑膜控制NFTSM是基于TSM而产生,优点是在远离平衡点区域可有效增加状态导数的绝对值,这将有效提高终端的收敛速度,而在近平衡点时则以TSM方式快速收敛.同时“终端吸引子”的引入,在兼顾系统非奇异特性的同时也有效地解决了滑模控制系统的“抖振”问题.因此,这里选取NFTSM作为LSC系统的控制策略.则滑模面的数学函数为

(11)

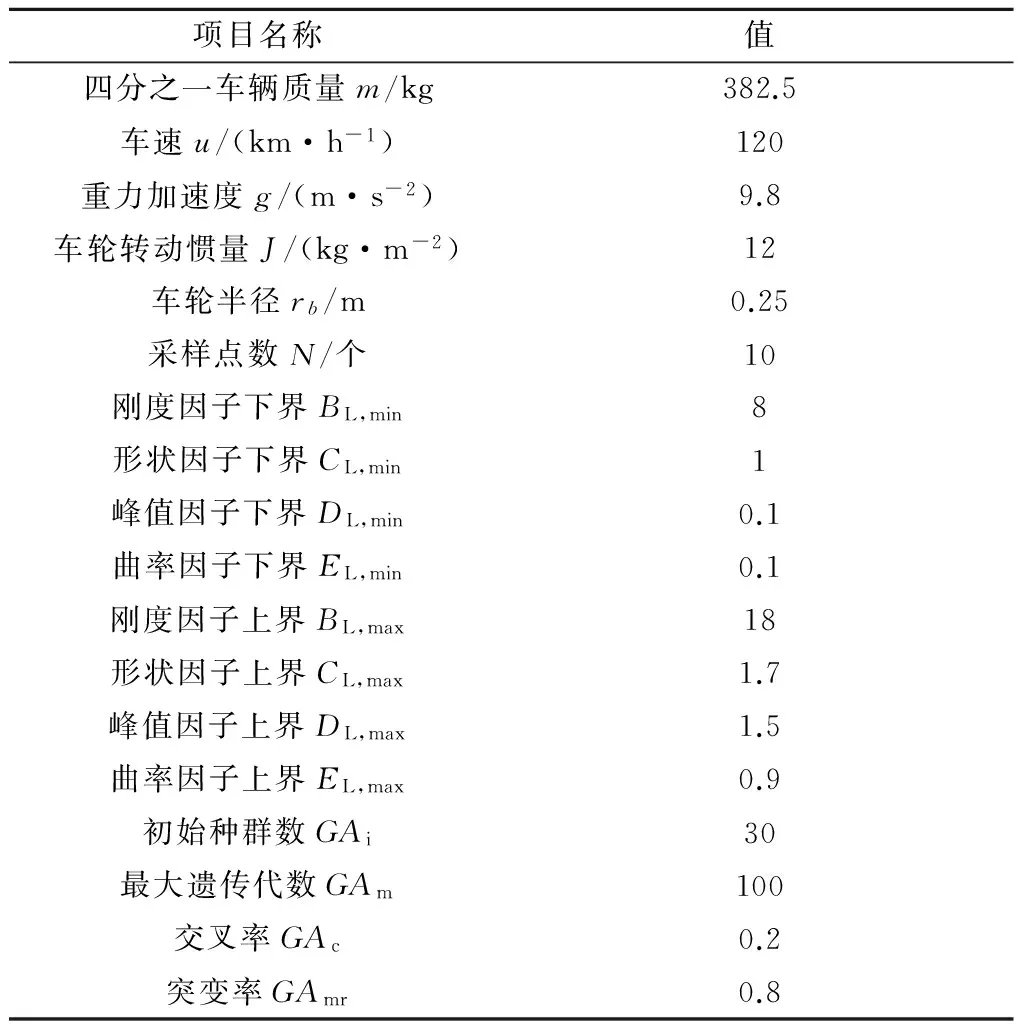
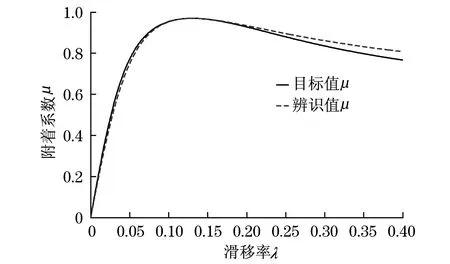
式中：e∈R，是滑移率与目标值之间的差值，即跟踪误差;R代表实数集;α,β是定值且α>0;p,q是给定正奇数且p

(12)

联合方程(5),(6)和(12),可得:

(13)

式中:J是车轮转动惯量.

为完全消除控制律中的非线性切换项,避免系统抖振,通常使用“吸引子”设计滑模控制律.其中终端吸引子是可使滑模控制状态变量在有限时间内到达滑模面,且对模型误差和外部干扰具有较好的鲁棒性,在滑模控制中得到广泛应用,本文针对NFTSM的特点,在传统终端吸引子的基础上增加e(p/q)-1项,获得一种新的吸引子:

(14)

式中：φ，R分别为滑膜面系数，φ∈R+，γ∈R+;m和n是正奇数且 0

联合方程(11)—(14),得到NFTSM的控制率Tb:

(15)

5 仿真试验结果及分析

本节中通过不同的仿真试验对所提出的控制系统的性能进行验证.首先,也是最重要的一个环节,对参考轮胎模型的参数辨识结果进行验证.然后,对基于NFTSM的LSC控制系统的跟踪能力进行验证,同时将NFTSM的控制能力与NTSM进行对比验证.最后,在对接路面工况下,对自调节LSC控制系统进行整体的仿真验证.

5.1 参数辨识结果仿真验证

表1给出了不同路面工况下魔术公式参数的测量值,通过这些信息可以分别获取各种路面下轮胎模型参数BL,CL,DL和EL的上下边界值.表2给出了仿真试验所用到的参数值.

表1 不同路面下轮胎模型的参数值

表2 仿真试验所用参数

图4 滑移率和摩擦系数关系图

5.2 对接路面工况下自调节LSC的仿真试验

在对接路面工况仿真试验中,轮胎-地面力FR在0.5 s后变为2 420 N.在1.5 s时,车辆由干燥沥青路面驶入湿滑沥青路面.仿真结果如图5—7所示.

图5 轮胎-地面力跟踪性能

图6 轮胎-地面力跟踪误差

图7 车辆加速度

6 结论

本文重点关注分层集成控制系统中伺服环执行机构在复杂多变的路面工况下自调节跟踪控制系统的关键问题.提出了轮胎-地面力参数优化估计的两步骤方法,选取魔术公式作为轮胎参考模型,并设计基于有约束混合遗传算法的在线优化算法,采用数值方法计算得到目标滑移率,为LSC系统做好准备工作.然后,结合NFTSM方法设计自调节LSC控制系统.最后,通过仿真试验对整个自调节系统进行验证,结果证明所提出的控制系统是有效的.

[1] XIAO Hansong,CHEN Wuwei,ZHOU Huihui,et al.Integrated control of active suspension system and electronic stability programme using hierarchical control strategy:theory and experiment[J].Vehicle System Dynamics,2011,49(1):381-397.

[2] GORDON T,HOWELL M,BRAMDAP F.Integrated control methodologies for road vehicles[J].Vehicle System Dynamics,2003，40(1):157-190.

[3] NAGAI M,SHINO Z,GAO F.Study on integrated control of active front steer angle and direct yaw moment[J].JSAE Review,2002,23(3):309-315.

[4] YU Fan,LI Daofei,CROLLA D A.Integrated vehicle dynamics control-state-of-the art review[C]∥Proceedings of the Vehicle Power and Propulsion Conference,2008,New York:IEEE,2008:835-840.

[5] HE Z,JI X.Nonlinear robust control of integrated vehicle dynamics[J].Vehicle System Dynamics,2012,50(2):247-280.

[6] MOKHIAMAR O,ABE M.Simultaneous optimal distribution of lateral and longitudinal tire forces for the model following control[J].Journal of Dynamic Systems,Measurement and Control,2004,126(4):753-763.

[7] FURUSHO H,AOKI Y,ISHIGC T,et al.Adaptive slip control using a brake torque sensor[C]∥FISITA World Automotive Congress 2008,Congress Proceedings-Vehicle Safety,Berlin:Springer Automotive Media,2008:155-163.

Study on tyre friction control based on non-singular fast terminal sliding mode

TONG Guang,WANG Qiang

(College of Automobile, Shanghai Dianji University, Shanghai 201306, China)

Based on the longitudinal tyre friction control, the relevant coefficient via the magic formula and key parameters under different road surfaces are identified on-line through the proposed constrained hybrid genetic algorithm (GA).For a specific tyre friction, the corresponding control objective of slip ratio is first obtained using a numerical method.Then, a nonsingular fast terminal sliding mode (NFTSM) control method is employed to track the desired slip ratio, i.e.longitudinal slip ratio control (LSRC).Evidently, such serial algorithms as parameter evaluation, optimization and control are adapted to the variation of road surfaces.Finally, it is concluded from simulation experiments that the tyre friction can be tracked precisely and rapidly to meet the adaptation requirement upon road surface variation.

parameter identification; tyre friction control; constrained hybrid genetic algorithm; nonsingular fast terminal sliding mode control

上海电机学院环卫装备学科资助项目(12XKJ01)

仝 光(1978-),男,讲师.E-mail:tongg@sdju.edu.cn

文献标志码：A 文章编号：1672-5581(2016)03-0244-05