基于精确建模的齿轮传动线外啮合冲击研究
符双学,周长江
(1.广州民航职业技术学院,广州 510403; 2.湖南大学汽车车身先进设计制造国家重点实验室,长沙 410082)
基于精确建模的齿轮传动线外啮合冲击研究
符双学1,周长江2
(1.广州民航职业技术学院,广州 510403; 2.湖南大学汽车车身先进设计制造国家重点实验室,长沙 410082)
根据齿轮啮合原理,准确求解出复杂的齿廓曲线; 采用MATLAB-APDL混合建模方法,创建精确的齿轮有限元模型,对齿轮传动线外啮合冲击问题进行了研究,推导出齿轮啮合冲击碰撞数学模型,通过实例计算,求出了冲击速度与冲击力、齿宽与冲击力的数量关系,获得了比较精确的冲击时间.线外啮合冲击的深入研究,对改善齿轮传动性能和提高齿轮设计制造水平具有一定的意义.
精确建模; 齿轮传动; 线外啮合; 冲击
传动齿轮冲击研究对于减少摩擦损失、增大轮齿承载能力、改善系统传动性能等具有显著的意义.因轮齿的受载变形、加工误差、在理论啮合线外发生啮合等而产生的啮入与啮出冲击,称为啮合冲击.啮合冲击会加速齿轮的点蚀形成、齿根裂纹的萌生与扩展,及轮齿的断裂,同时又影响到齿轮系统的动态特性,是重要的振动与噪声激励源.
国内外学者对齿轮线外啮合的冲击问题做了很多研究,WINTER将线外啮合冲击列为齿轮传动振动与噪声的三大原因之一; MUNRO[1]等对线外啮合与传递误差的关系进行了研究,推导出了定量的计算公式; SMITH[2]把传递误差作为齿轮振动噪声的激励源,研究了齿轮动力学问题; WECK 、JAO分析了线外啮合冲击与齿轮点蚀破坏之间的关系[3-4]; 姚文席等[5]研究了啮入冲击的动态响应; 武保林等[6]给出了基于机械动力学理论和能量守恒定律的线外啮合冲击力的计算公式.
对于线外啮合对齿轮承载能力、振动、噪音、摩擦磨损等方面的影响,学者们做了许多有益的研究.但在连续体弹性动力学层面,对线外啮合的冲击力、冲击时间与相应的冲击应力等问题尚缺少深入研究.齿轮啮合冲击问题的本质是连续体弹性体动力冲击碰撞问题,目前的研究都把这一问题当成集中质量的碰撞问题,冲击问题本身是一个强非线性问题,冲击过程极其复杂,解析方法无法准确的求解这一问题.本文采用MATLAB-APDL混合建模方法,创建精确的齿轮线外啮合有限元模型,基于LS-DYNA动力学仿真系统,对啮合冲击问题进行了研究,给出了齿轮啮合冲击碰撞的数学模型,通过实例计算,对冲击过程进行了数值模拟,得出了冲击力与冲击时间,齿宽与啮合冲击力的数量关系.
1 齿轮几何模型的建立
1.1 齿轮及其材料特性参数
计算模型用到的齿轮参数见表1,齿轮的材料特性见表2.功率P=15 kW,转速n1=2 000 r/min,传动比为1.齿轮精度6级,标准安装,不计轮齿误差及轴、齿轮箱变形; 齿形粗短,考虑剪切.

表1 齿轮参数

表2 齿轮材料特性
1.2 轮齿几何模型的生成
齿廓由无凸台、压力角为20o的标准滚刀加工而成; 不考虑加工过程中刀具和齿轮毛坯相互挤压产生的弹性变形.标准滚刀齿形如图1所示,其中直线部分切出齿轮的渐开线,刀具圆角部分切出过渡曲线,加工出的轮齿如图2所示.
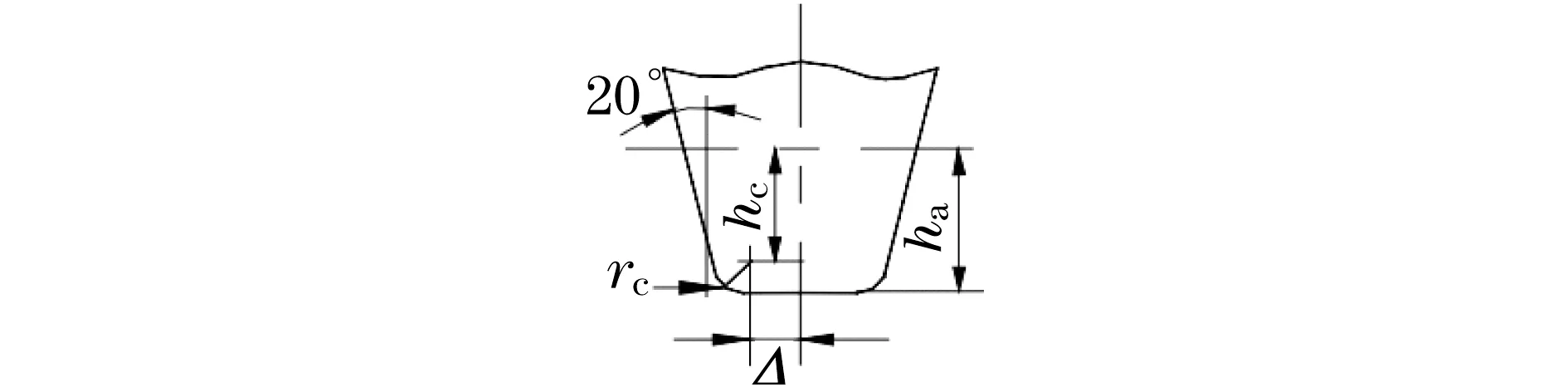
图1 滚刀齿形
渐开线方程为
(1)
式中:x,y分别为渐开线方程的横坐标和纵坐标;γi为齿廊上任意点至齿轮轴心的距离;γ=(π/2z)-(invxi-invx),αi为齿廊上任意点的压力角.
过渡曲线方程为:
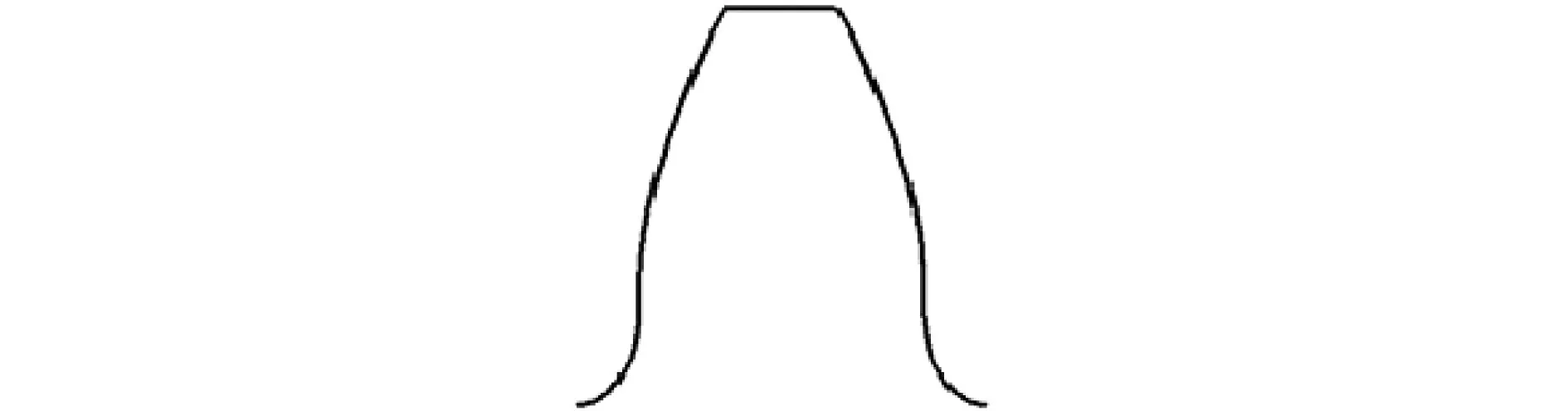
图2 轮齿齿廓
(2)


图3 三维精确齿形
根据式(1)和(2),在MATLAB中编程准确求解出齿廓曲线,并“写入”纯文本数据文件; 由APDL(ANSYS Parametric Design Language)编程“读出”,在ANSYS图形窗口中生成齿廓,完成较复杂的轮齿部分几何建模,齿轮几何模型见图3.基于纯文本数据文件的APDL与MATLAB混合编程,可创建复杂的齿轮有限元几何模型.
2 齿轮啮合的弹性冲击碰撞动力学模型
2.1 齿轮啮合冲击分析
在齿轮啮合过程中,一对理想齿轮正确啮合的条件是它们的法节相等,即Pb1=Pb2.但实际上由于存在轮齿误差和变形,使得Pb1≠Pb2.这样,轮齿在啮入点和啮出点会偏离理论啮合线,从而导致齿轮传动在啮合开始与结束时发生啮入与啮出冲击.
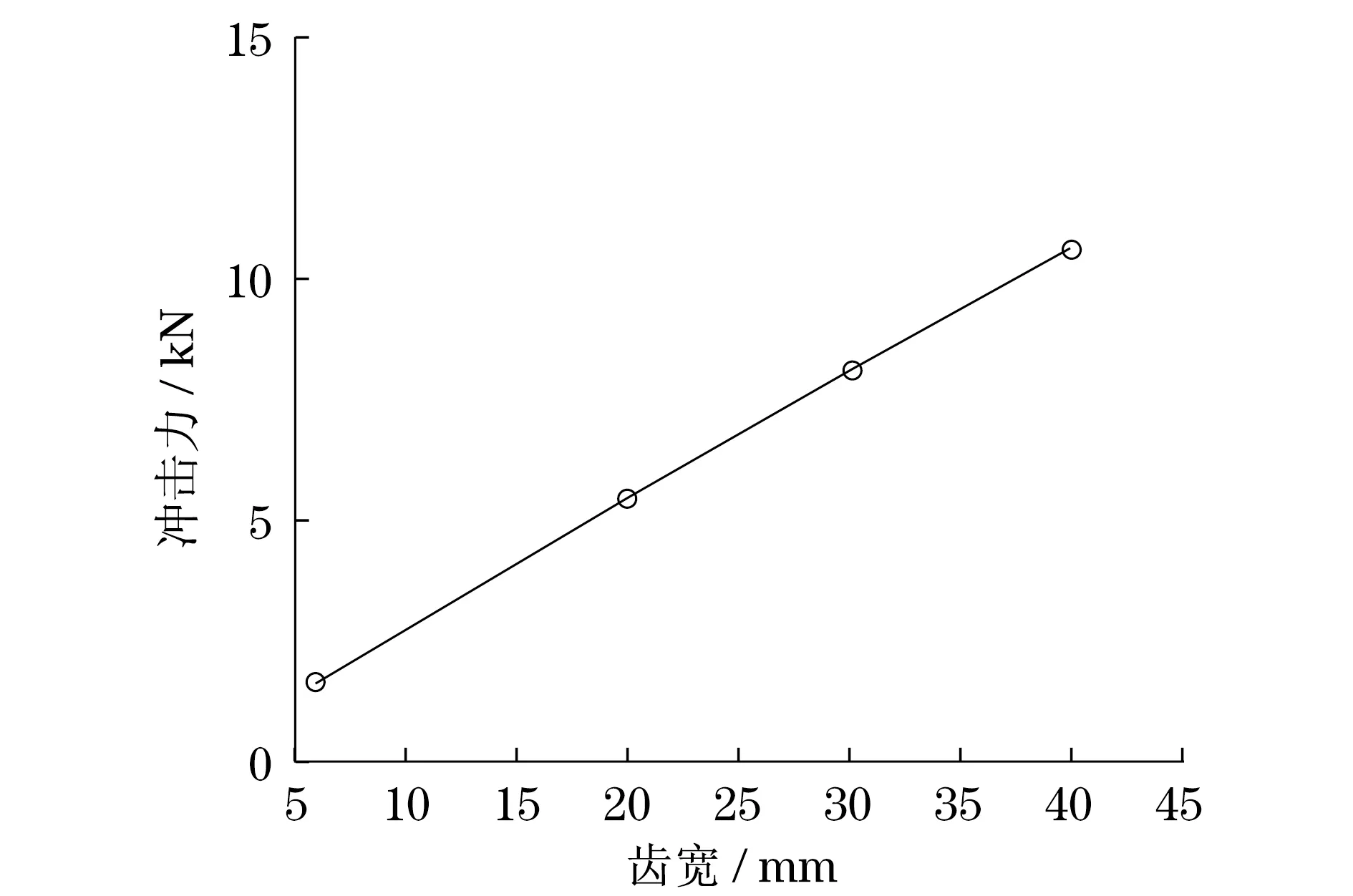
研究表明,啮入冲击的影响明显比啮出冲击大,现主要讨论啮入冲击对齿轮强度的影响.当Pb1 图4 齿轮啮入冲击示意图 图5 齿轮啮合冲击力学模型建模示意图 2.2 基于弹性冲击碰撞理论的齿轮啮合冲击力学模型 齿轮啮合冲击问题属于弹性动力学范畴,根据文献[9],线弹性小变形动力学基本控制方程为 (3) 边界条件 (4) 式中:ui(x,t)为x点在t时刻的位移. 图5是对应于图4的齿轮啮合冲击力学模型建模示意图.在弹性冲击碰撞问题中,除了考虑变形体的应变能以及外力势能外,还须考虑物体的动能,建立包含这些能量在内的泛函数,由它们的驻值条件便可以得到弹性动力学的控制方程以及定解条件. 由Hamilton变分原理可建立齿轮啮合冲击的弹性动力学控制方程以及定解条件,采用的初值条件为u(x,0)=u0(x),u(x,t1)=u1(x),其中,u0(x)和u1(x)为给定的函数,保留几何方程、物理方程与位移边界条件.满足上述方程的状态称为可能运动状态,即约束所允许的运动状态.由Hamilton变分原理有: (5) 将K与U代入式(5)中,逐项进行变分运算,可以得到: (6) 由于(σijδui),j=σij,jδui+σijδui,j,pi=σijnj,(nj为法向量)代入式(6)中,并应用散度定理得出: (7) 将主、从动齿轮的结构空间离散化,在离散化的单元以及节点上进行位移ui(x,y,z,t)插值,即 (8) ∫VρfNTdV-∫sσPNTdS]δUdt=0 (9) 令M=∫VNTρNdV,K′=∫VBTEBdV,F1=∫Vρf′NTdV,F2=∫sσPNTdS.由δU的任意性,有 (10) (11) 式(11)中,阻尼矩阵C工程上一般采用比例阻尼计算方法,即 (12) 系数α0,α1可以由试验方法或经验确定. 动力方程式(11)的求解方法采用显示中心差分法,假定0,t1,t2,…,tn时刻的节点位移、速度与加速度均为已知,现求解tn+1(t+Δt)时刻的结构响应.中心差分法对加速度、速度的导数采用中心差分代替,即 (13) 将式(13)代入式(11)中,整理后得 (14) 3.1 冲击力与冲击速度的关系 由图4可得实际啮入点D的位置公式: (15) 式中:η为O2D与O1O2的夹角;r1,r2分别为主动齿轮和被动齿轮的节圆半径;ra2被动齿轮和齿顶圆半径. 由图6可知,冲击力随着冲击速度的增加而增大.齿侧的间隙是不变的,因此主动轮初速的增加,将引起轮齿冲击过程的提前,提前的时间随初速的增加而增大. 根据文献[7]可知最大冲击力与速度的关系式为 (16) 式中:J1,J2分别为齿轮1,2的转动惯量;rb1,rb2分别为齿轮1,2瞬时啮合线对应的瞬时基圆半径;qs为齿轮在初始啮入点D处的综合柔度. 在已知冲击速度的情况下可求出的最大冲击力的解析解,与数值仿真结果的对比情况如下表3所示. 3.2 冲击力的作用时间 利用LS-DYNA可得到不同冲击速度下冲击力作用时间的准确值,如表4所示. 图6 冲击力随时间变化曲线 根据文献[5],啮合冲击时间近似计算公式为 (17) 式中:Tz是理想齿轮理论上的换齿时刻;t0是齿对进入啮合的瞬时时刻.计算表明,Δt一般是Tz的5%~10%;z1是出轮1的齿数;ω1是齿轮1的角速度. 表3 冲击力的解析解与数值仿真结果的对比 表4 冲击力作用时间与冲击速度对应表 按文献[5],Δt为一次完整的啮合冲击过程的时间,即图4中齿轮啮合运动从D点到E点的时间; 而表4中列出的冲击时间为冲击力作用的时间,即两物体接触碰撞时弹性变形的时间,两者的定义不同,在数值上不具备可比性.但是由表4可知,随着冲击速度的提高,冲击时间略有减小.这与式(17)中ω1增大Δt减小的趋势一样的,说明冲击时间与主动轮转速有关,与冲击速度有关. 3.3 冲击力与齿宽的关系 根据理论力学 (18) 式中:ρ为密度;b为齿宽;rh为齿轮内腔半径;rb1、rb2′分别为瞬时啮合线对应的瞬时基圆半径,如图4所示. 将(18)式代入到(16)式中,可得冲击力与齿宽的关系式 (19) 同样利用LS-DYNA仿真,得出了不同齿宽下的最大冲击力值.如图7所示.由图7可知,最大冲击力随着齿宽的增加而增大.这是因为在其他参数不变的情况下,齿轮齿宽增加,则齿轮质量增大,冲击必定加剧. 图7 v=0.5 m·s-1时不同齿宽下的最大冲击力 (1) 基于齿轮啮合原理,采用MATLAB-APDL混合建模方法,创建了精确的齿轮有限元模型. (2) 齿轮线外啮合冲击时,冲击速度对冲击力的影响非常大,因此在齿轮传动的减震降噪、摩擦与磨损上,适当地减小冲击速度是非常有效的手段. (3) 在冲击速度不变的情况下,齿宽越宽冲击力越大. (4) 冲击作用时间可通过数值仿真精确求出,其值随着冲击速度的增大而减小,冲击时间的精确求出为冲击的动态响应奠定了基础. [1] MUNRO R G,MORRISH L,PALMER D.Gear transmission error outside the normal path of contact due to corner and top contact[J].Journal of Mechanical Engineering Science,1999,213(3):389-399. [2] SMITH D J.Gear noise and vibration[M].New York:Marcel Dekker,2000. [3] WECK M G.Optimum tooth flank corrections for helical gears[J].Journal of Mechanical Design ,1990,112(4):584-589. [4] JAO T C,DEVLIN M T.Influence of surface roughness on gear pitting behavior[J].Gear Technology,2006,23,(3):31-38. [5] 姚文席,魏任之.渐开线直齿轮的啮合冲击研究[J].振动与冲击,1990,36(3):57-62. YAO Wenxi,WEI Renzhi.The shock research on meshing teeth of involute spur gear[J].Journal of Vibration and Ahock,1990,36(3):57-62. [6] 武保林,杨素君,姚俊红.齿轮传动中啮合冲击的理论分析[J].机械科学与技术,2003,22(1):55-57. WU Baolin,YANG Sujun,YAO Junhong.Theoretical analysis on meshing impact of involute gears[J].Mechanical Science and Technology,2003,22(1):55-57. [7] 符双学.齿轮传动齿面摩擦因数反求研究[D].长沙:湖南大学,2008. FU Shuangxue.Computational inverse studies of teeth friction coefficients in gear drive[D].Changsha:Hunan University,2008. [8] 肖利民,唐进元.低噪声齿轮设计方法[J].制造技术与机床,1995(5):30-33. XIAO Limin,TANG Jinyuan.A new design method for low noise gear[J].Manufacturing Technology & Machine Tool,1995(5):30-33. [9] 白金泽.LS-DYNA3D理论基础与实例分析[M].北京:科学出版社,2005:10-100. BAI Jinze.LS-DYNAN3D theoretical basis and case analysis[M].Beijing:Science Press,2005:10-100. Corner contact impact on gear transmission based on accurate modeling FU Shuang-xue1,ZHOU Changjiang2 (1.Civil Aviation College Guangzhou, Guangzhou 510403,China;2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082,China) Based on the gear engagement principles, the exact curve of tooth profile is produced.With composite modeling via MATLABTM and APDLTM, a precise FEM gear model is established.Upon completion of the mathematical model for gear meshing impact and collision, the corner contact impact process is simulated to quantitatively obtain the relationships between impact velocity and force, as well as between gear breadth and impact force.Therein, the accurate impact timing can improve the performance of gear transmission and upgrade the gear design and manufacturing level. accurate modeling; gear transmission; corner contact; impact 国家自然科学基金(50805044); 广东省高等学校优秀青年教师培养计划项目(YQ2014178)资助 符双学(1979-),男,副教授.E-mail:25272505@qq.com TH 132.41 A 1672-5581(2016)03-0221-06





3 数值仿真及分析



4 结论

