高职“逻辑函数化简”教学手记
许智勇
(湖南铁路科技职业技术学院 湖南株洲 412000)
高职“逻辑函数化简”教学手记
许智勇
(湖南铁路科技职业技术学院 湖南株洲 412000)
高职院校逻辑函数化简的教学,是个难点。如果在教学中注意循循善诱,引导学生积极参与适时总结,将会收到满意的教学效果。
常用运算律 一题多解 卡诺图
逻辑函数化简的意义是节省集成电路数目,焊接点减少,还可大大提高电路的可靠性。[1]
在实际问题中,往往首先将电路化简成最简与或式,用代数法化简的过程中,还常用到普通代数的提取公因式法、分组法、去括号法等,有时还根据需要利用公式进行添加项后,再进行分组化简。在逻辑运算基本公式中,我们应当牢记以下几个常用结论。[2]

由上述例题看出,代数法化简逻辑函数,既需要牢记一些公式,又带有技巧性,掌握起来比较困难,但作为数字电路化简的一个基本工具,还是应该掌握一些常用的代数化简法。对多变量函数的化简,相对代数化简法,卡诺图法要容易得多。
我们知道,凡两个逻辑相邻项可合并成一项,按照这个规律,可以把逻辑函数中的各个最小项用图形表示出来,这种图就叫卡诺图。需要强调的是,为了符合相邻原则,两个逻辑变元(或其否定)的乘积的排列顺序必须是00、01、11、10,这样排列就保证了纵横相邻小方格里的最小项都是相邻的。
因为卡诺图的每一个小方格都唯一地对应一个最小项,所以要用卡诺图来表示某逻辑函数,应该先将函数表达式化成最小项之和(主析取范式)。这比较麻烦。如果函数表达式已经是析取范式,则可以快速填写卡诺图。
解 由变量D知道,这是一个四变元函数。
由第三项B C知道,它与A、D无关,可以写作×B C×,在既符合B=1(01、11两行)又符合C=1(11、10两列)的交叉方格内填入1即可。由第四项知道,它与A无关,可以写作在卡诺图中0000格和1000格内填入1即可。至此可得到函数F的卡诺图。剩下未填入1的格内应为0,这里省去是为了使卡诺图更加清晰。
用卡诺图化简逻辑函数的一般步骤:
①确定变元的个数,画出相应的卡诺图,并把函数F表达式中的相应项填入1,其余小方格内填入0或者省去不填。
② 对卡诺图中有“1”的方格画相邻区域圈,画圈时要按2、4、8、16格为单位,遵循的原则是:圈越大越好,这样各与项中所含变元就越少;圈的总数越少越好,与项的项数就越少。
③ 将每个圈中的公有变元因子找出来,得到对应的“与”项,并把各个圈得到的与项相加(或)起来,便得到化简后的最简与或表达式(主析取范式)。
具体操作时,要特别注意四角相邻、左列与右列相邻、顶行与底行相邻。首先将与其他任何“1”方格都不相邻的孤立“1”方格单独圈出来;其次找出那些仅与另一个“1”方格唯一相邻的“1”方格,将它们两两相圈组成含有两个“1”方格的相邻区域;最后,再依次将含有四个“1”方格、八个“1”方格的相邻区域画出来。
在画相邻区域时,有些“1”方格可以被多个圈公用,这种区域间的重叠现象是允许的,但每个圈中必须含有至少一个新“1”,即别的圈中都未包含进去的1。这样做,就可以避免在化简后的函数中出现多余项,使化简后的与或表达式为最简形式(主析取范式)。
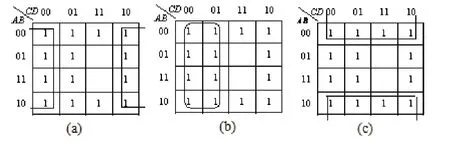
解 这是个四变元函数,其卡诺图如图所示。可画出三个圈分别如图(a)、(b)、(c)所示,仔细检查,每个圈中都包含有至少一个其他两个圈未包括进去的新1,故没有多余的圈。
[1] 王信峰.计算机数学基础[M].高等教育出版社,2009.
[2] 许智勇.如何让高职数学课生动起来[J].河南教育旬刊,2011年第6期.

