旋转带电体磁矩的推广的平行轴定理
周国全
(武汉大学 物理科学与技术学院,湖北 武汉 430072)
教学讨论
旋转带电体磁矩的推广的平行轴定理
周国全
(武汉大学 物理科学与技术学院,湖北 武汉 430072)
首先推导出二阶标量电矩在任意两个平行轴之间的移轴定理(平行轴定理)的最一般的表达形式;再通过旋转带电体的定轴磁矩与其二阶标量电矩的简单比例关系,推导出定轴旋转带电体的磁矩在任意两个平行轴之间的移轴定理的推广形式; 再具体讨论了过电荷中心的轴与其平行轴之间的移轴定理,并特别给出了旋转带电体的磁矩的平行轴定理在如下三种特定情形的具体形式:1)总电荷为零,2)电偶极矩为零,3)总电荷与电偶极矩均为零.最后澄清了若干文献中有关平行轴定理的含糊不清之处,并更正其错讹之处.
旋转带电体;磁矩;平行轴定理;电荷中心;磁偶极矩
旋转带电体磁矩的计算及其规律的研究,是电磁场理论及其应用研究的一项重要内容.从电磁场理论、空间技术及天体物理的角度出发,深入研究旋转带电体的电磁特性及其在外场中的动力学与运动规律具有特殊而重要的意义[1,2].文献 [2-4]通过引入诸如电矩张量、标量电矩、磁矩椭球、主轴及主轴标量电矩等一系列有用的概念,推导出任意带电体绕定点或定轴转动的磁矩的若干规律.文献[4]明确给出了任意给定电荷分布的旋转带电体的零磁矩条件.文献 [5-7]基于旋转带电体磁矩和刚体转动惯量之间严格而精致的类比关系,成功地导出了诸如正交轴定理及其推广、平行轴定理及其推论、中心轴定理等若干重要的计算法则及其算例.文献[8,9]基于旋转带电体的磁矩的张量表达,利用经典力学中转动刚体的欧拉方程,导出了匀强磁场中定点转动带电刚体的拉格朗日动力学理论和欧拉方程;严格地解决了两种简单对称情形.文献[10]则讨论了在匀强磁场中定点转动的带电绝缘体转动的稳定性问题.
本文专注于旋转带电体定轴磁矩的一条重要法则---平行轴定理;该定理的推导及其应用,已然见诸于若干文献[5-7].它们的合理与正确性基于一种力电类比关系,即当电荷元dq绕定轴作角速为 ω、转动半径为 r⊥的匀角速转动,则其磁矩大小为这与质量为dm的质点绕定轴作半径为r⊥的转动时的转动惯量dJ=r2⊥dm具有如下类比关系:

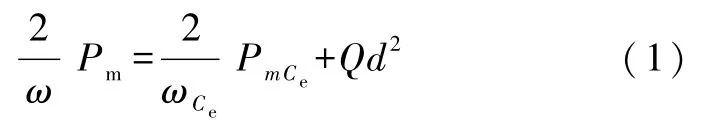
基于数学表达的简洁性的要求,不妨取 ω=ωCe(在物理上ω、ωCe本来相互独立),文献[3,4]给出了如下形式的平行轴定理:
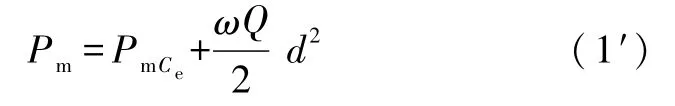
这就是旋转带电体的磁矩的平行轴定理,鉴于刚体转动惯量的平行轴定理的普适性,上述定理式
(1或1′)似乎对任意形状,任意电荷分布 (体分布、面分布或离散点分布)的旋转带电体都成立.
仔细推敲,定理式(1或1′)暗含一个重要而直接的推论:“当旋转带电体之电荷总和 Q=0时,Pm=PmCe,与两轴间距d及移轴方向无关.即若带电体各处电荷面密度或体密度不为零但总电荷为零,则其绕空间任一轴的磁矩恒等于同一角速下绕过电心的平行轴的磁矩,与两轴间距及移轴方向无关,或者说与转轴位置无关,仅与转轴方向有关”.但作者深入研究的结果表明,定理式(1或1′)在特定条件下的推论具有局限性甚至谬误,它被掩盖在不严格的一般性条件的描述之中.最典型一个错讹之处,在于运用类比法推导旋转带电体定轴磁矩的平行轴定理时,质点系统的质心是正定和必然存在的,而电荷系统的中心却不是正定的,在总电荷 Q(即零阶电矩)为零时,由所定义的电荷中心Ce甚至根本不存在,此时文献[1,2]中的平行轴定理就失效而不成立,因而“在总电荷为零时,旋转带电体的定轴磁矩与位置无关,仅与方向有关”的结论显然也是站不住脚的.
本文首先推导旋转带电体的定轴磁矩在两个任意平行轴之间的移轴定理的最一般的形式,分析了定轴磁矩与移轴无关的充分条件,再讨论了在1)总电荷(零阶矩)为零,2)电偶极矩(一阶矩)为零,以及3)零阶矩与一阶矩均为零的特定条件下,旋转带电体的定轴磁矩的平行轴定理的特殊的具体形式,进而理清文献 [5-7]中的平行轴定理的模糊与错讹之处.
1 旋转带电体定轴磁矩的推广的平行轴定理
由于旋转带电体的定轴磁矩与电荷沿轴向的分布无关,因此假设两平行的定轴方向垂直于纸面并分别与纸面相交于O与O′处,分别选定为z轴(以O点为坐标原点)与 z′轴(以 O′点为坐标原点),则任一点电荷qi(i=1,2,…,N),(一般并不一定在纸面),在两个坐标系中的位矢与坐标分别为ri(xi,yi,zi)与 r′i(x′i,y′i,z′i),但具有相同的 z坐标,即zi=z′i.根据文献[1-3],电荷元dq绕定轴(O,l)作角速为ω(大小为ω)、转动半径为r⊥的匀角速转动时,其定轴磁矩大小为[2-7]
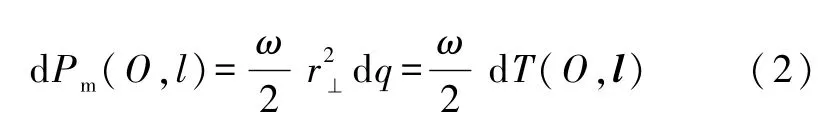
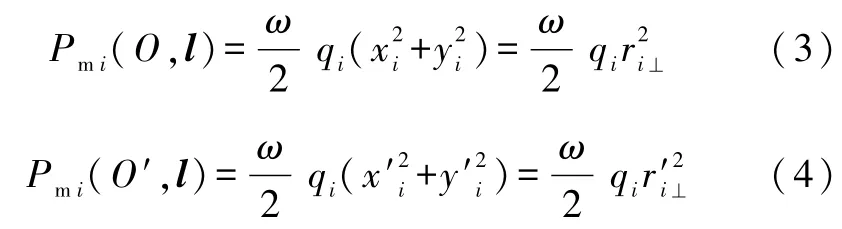
再对指标i(i=1,2,…,N)求和,可得带电体绕两轴的总磁矩分别为:
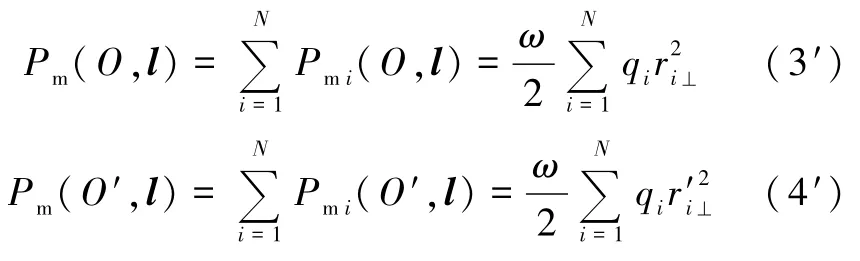
在此基础上,我们来讨论旋转带电体磁矩的平行轴定理(移轴定理).我们首先讨论旋转带电体的定轴磁矩在两个任意平行轴之间最一般的移轴定理.
如图1所示,在此平面上,我们不妨假设电量为qi的第i个点电荷相对于点 O的位置矢量为 ri;其相对于点O′的位置矢量为r′i;两轴之间的相对位置向量并满足如下关系式

图1. 在两个任意平行轴之间的移轴定理

将以上方程两边的矢量与自己相点乘,可得

两边同乘以第i个点电荷的电量qi,并移项可得
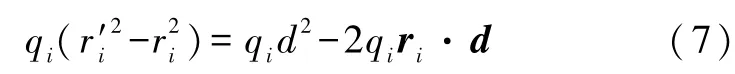
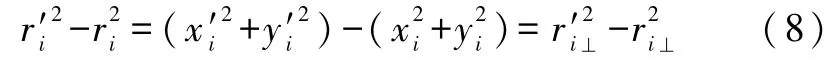
将式(8)代入式(7)左边,再对式(7)中的指标i(i=1,2,…,N)求和,可得其中称为该电荷系统的零阶电矩,即总电荷称为该电荷系统的关于定点 O
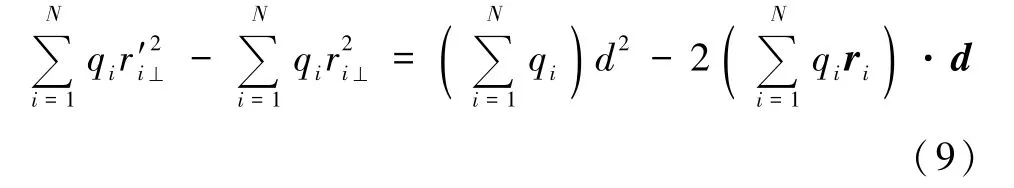
的一阶电矩,即电偶极矩,而统相对于 O处的定轴的二阶电矩,记为 T(O,l),称为该电荷系称为该电荷系统相对于O′处的平行定轴的二阶电矩,记为T(O′,l),于是可得二阶电矩平行轴定理
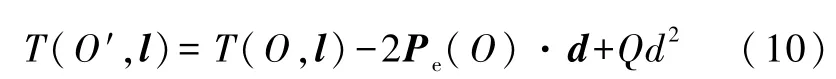
将式(10)两侧同乘以角速矢量之半 ω/2,运用式(2),或式(3′)、(4′),亦即旋转带电体的定轴磁矩公式[2-4]可得定轴磁矩在任意平行轴之间的移轴定理

这是旋转带电体的定轴磁矩的移轴定理的最一般的形式.以下基于式(10)与式(11)就若干特例情形进行进一步的讨论.
2 若干特例情形的讨论
不难发现,当零阶电矩Q=0的同时,一阶电矩Pe(O)=0,或 Pe⊥d,定轴磁矩在两个任意平行轴之间满足移轴不变性,即
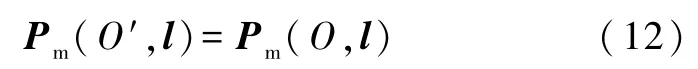
当零阶电矩Q≠0,但一阶电矩Pe(O)=0,或轴的横向平移方向 d⊥Pe(O)时,定轴磁矩在任意两平行轴之间满足如下移轴定理:
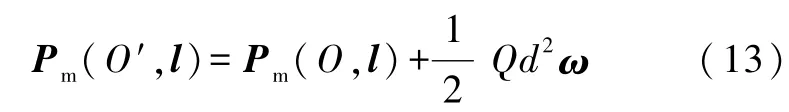
当零阶(标量)电矩(即总电荷)Q=0,但一阶(矢量)电矩(即电偶极矩)Pe≠0时,定轴磁矩在任意两平行轴之间满足如下移轴定理:
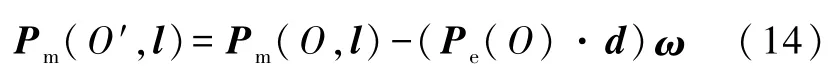
其次我们再讨论旋转带电体的定轴磁矩从过电荷中心的轴向其他平行轴的移轴定理.当Q≠0时,有
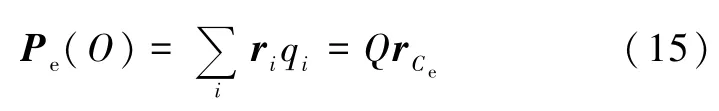
其中rCe是电荷中心的位置矢量,其定义为
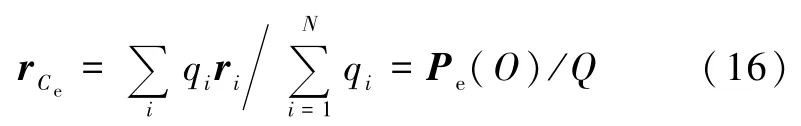
若将点O取成电荷中心 Ce,此时 rCe=0,因而电偶极矩

则电矩平行轴定理式(10)变为

形式上完全类似于质点系的转动惯量的平行轴定理.将式(18)两侧同乘以角速矢量之半同样运用旋转带电体的定轴磁矩与标量二阶电矩的比例关系式(2),立即可得磁矩与电荷中心 Ce有关的平行轴之间的移轴定理式(1)或(1′).这种情形下,我们再不能讨论式(18)在Q=0时的推论,这是因为Q=0时不存在电荷中心Ce,式(18)已不再成立.
3 结论
旋转带电体的磁矩计算的平行轴定理的最一般的推广形式(11),适用于任意两个平行的定轴之间和一切具有确定电荷分布的情形.定理式(11)及其特殊情形的诸推论式(13)、(14),以及Q≠0时关于电荷中心的定理式(1)或(1′),为我们精确计算各种形状的旋转带电体沿任意轴的磁矩提供了强有力的理论工具,因而对完善电磁场理论的研究与推进其技术的应用发展尤为必需和重要.研究结果表明:1)当带电体的零阶电矩(即总电荷)为零时,电荷中心不存在,文献[5-7]的平行轴定理不再成立,而是本文的式(11)成立;2)当带电体的零阶电矩(即总电荷)为零,且其一阶电矩(即总电偶极矩)亦为零,或电偶极矩垂直于移轴方向(d的方向)时,其定轴磁矩才与轴的位置无关,仅与轴的方向有关.至此文献 [5-7]在带电体总电荷为零时的含糊与错讹之处得以澄清.
[1] 虞国寅,周国全.电动力学[M].武汉:武汉大学出版社,2008:11,87-88.
[2] 周国全.一个新的电矩张量及其在电磁场中的应用[M].金琅学术出版社(Golden Light Academic Publishing),(德国)萨尔布吕肯市:OmniScriptum GmbH&Co.KG.2015:11-25.
[3] 周国全.电矩张量与旋转带电体的磁矩[J].大学物
理,2007,26(4):7-11.
[4] Guo-Quan Zhou,et al.The Magnetic-Moment Quadric and Conditions of Vanishing Magnetic Moment for a Rotational Charged Body[J].Progress in Electromagnetics Research,2007,70:211-223.(Cambridge:The Electromagnetics Academy).
[5] 徐定藩,吕正山.带电体定轴转动的磁矩计算[J].大学物理,1997,16(4):3-4.
[6] 周国全.旋转带电体磁矩计算的若干法则与算例[J].物理与工程,2004,14(2):16-19.
[7] Guo-Quan Zhou.Several Rules about the Magnetic Moment of Rotational Charged Bodies[J].Progress in E-lectromagnetics Research Symposium(PIERS Online),2007,3(6):812-816.(Cambridge:The Electromagnetics Academy).
[8] Guo-Quan Zhou,et al.Charge Moment Tensor and its Application to a Rotational Charged Rigid Body in a Uniform Magnetic Field[J].J of Electromagn.Waves and Appl,2008,22:2179-2190.(Cambridge:The Electromagnetics Academy).
[9] 周国全,张斯磊,肖霄.带电电介质刚体在匀强磁场中的转动动力学方程[J].武汉大学学报(理学版),武汉:武汉大学出版社,2009,55(2):187-190.
[10] Guo-Quan Zhou.Rotational Stability of a Charged Dielectric Rigid Body in a Uniform Magnetic Field[J].Progress in Electromagnetics Research Letters,2009,11:103-112.(Cambridge:The Electromagnetics Academy).
The generalized parallel-axes theorem for the magnetic moment of a rotational charged body
ZHOU Guo-quan
(Department of Physics,Wuhan University,Wuhan,Hubei 430072,China)
The most general expression of the axis-translation theorem(parallel-axis theorem)for the 2-order scalar charge moment of a charge system around any two parallel axes is deduced.The generalized axis-translation theorem of the magnetic moment of a rotational charged body around any two parallel axes is derived through the simple proportionate relation between the fixed-axis magnetic moment and the 2-order scalar charge moment for the same charge system.The specific conclusions of axis-translation theorem are demonstrated and discussed under three cases:1)the total charge(0-order charge moment)is zero;2)the electric dipole moment(1-order charge moment)is zero;3)both the total charge and electric dipole moment are zero.The ambiguities are clarified and the mistakes in some
are corrected.
rotational charged body;magnetic moment;parallel-axis theorem;charge center;magnetic dipole moment
O 572,O 442
A
1000-0712(2016)11-0009-04
2016-01-18;
2016-05-09
国家级教学团队基金资助项目(202276003)
周国全,(1965-)男,湖北汉川人,博士,武汉大学物理科学与技术学院副教授,主要从事普物与理论物理教学,及场论与非线性可积方程研究工作.

