迈克耳孙干涉仪测折射率时的异常现象研究

南 阳，熊 畅，唐 芳，李朝荣

（1.北京航空航天大学 材料科学与工程学院，北京 100191；2.北京航空航天大学 物理科学与核能工程学院，北京 100191）

迈克耳孙干涉仪测折射率时的异常现象研究

南 阳1，熊 畅2，唐 芳2，李朝荣2

（1.北京航空航天大学 材料科学与工程学院，北京 100191；2.北京航空航天大学 物理科学与核能工程学院，北京 100191）

针对迈克耳孙干涉仪以激光为光源测量玻璃板折射率所产生的异常现象，本文从几何光学理论出发进行了讨论，简明直观地给出了干涉条纹吞吐转折点与零光程点、光程、虚光源相对位置之间的关系，并与实验数据进行了对比.

迈克耳孙干涉仪；吞吐转折点；折射率；几何光学；虚光源

迈克耳孙干涉仪是美国物理学家迈克耳孙（A.A.Michelson，1852-1931）在1883年利用分振幅方法制成的一种精密干涉仪，由于其设计精巧、光路直观、结构简单、测量精确等特点，广泛应用于科学研究和工程技术，透明物体折射率的测量也是一个重要应用.一般来说，由于白光相干长度小，从而干涉区间非常明确，偏离此区间后干涉条纹消失.对比于激光作为光源，白光的现象更加简单明确，从而在测量介质薄膜折射率时通常使用的光源是白光而不是激光.我们在尝试使用激光作为光源测量玻璃板折射率时，发现始终存在一种反直观的现象，玻璃板似乎会导致所在光路光程变小，从而得出玻璃板折射率小于1的错误结论.通过对比分析选择白光和激光作为光源的差异，我们对此异常现象进行了研究，采用几何光学方法简单又直观地阐明了其内在机制.

1 迈克耳孙干涉仪测量折射率的原理

图1所示为简易的迈克耳孙干涉装置原理图，G1是一面镀有半透半反膜的分束板，补偿板已省略，M1、M2为平面反射镜，M1是定镜，M2是动镜.G1将光源S0射来的光束一分为二，这两束光分别又被两块平面镜反射，当定镜M1与动镜M2严格垂直时，在观察屏E处形成等倾干涉圆环图样.利用白光测量待测物折射率时，在移动好仪器的基础上，将动镜M2移动至与 M1′重合的位置，即零光程差处.移动定镜 M1稍微倾斜，可观察到等厚干涉条纹，然后将待测物平行放置在M2前面，这时待测物所在光路的光程变大，要重新回到零光程差处就需要将M2向靠近G1的方向移动，当再次看到白光的等厚干涉条纹时认为再次回到了零光程差处.

图1 迈克耳孙干涉装置原理图

假设待测物厚度为d，折射率为n，动镜臂增大的光程为2（n-1）d.设再次回到零光程处时M2移动的距离为ΔL，则有

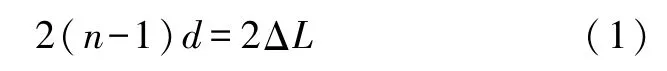
即可得到待测物的折射率为

2 测量折射率时的异常现象

本实验不使用传统的白光干涉而是使用激光迈克耳孙干涉实验来测量平板玻璃介质的折射率.实验中使用波长为632.8 nm的氦氖激光器作为光源，待测物为一块质地均匀的无机玻璃板，厚度约为1 mm.实验时发现在动镜臂和定镜臂光程相同的位

置处（不加玻璃板的零光程差处），在动镜前加上一块玻璃板，动镜臂的光程毫无疑问是增大的.当将动镜M2向靠近分束镜G1的方向移动时，动镜臂光程变小，两臂光程差变小，应该看到干涉条纹向里吞.继续沿同一方向移动M2，在越过新的零光程差点（加入玻璃板后的零光程差处）后两臂的光程差又开始变大，应该看到干涉条纹向外吐，因此整个移动M2的过程中预期观察到的实验现象应该是干涉条纹先吞入后变为吐出.反之，如果将M2向远离分束镜G1一侧移动则是干涉条纹一直吐出.

然而，我们在实验过程中观察到的实验现象却与之相反，当将 M2向靠近分束镜一侧移动时干涉条纹一直在往外吐出，而当M2向远离分束镜G1一侧移动时干涉条纹是先吞入后吐出.将待测物换成有机玻璃、石英比色皿等其他介质，结果也是如此.

图2所示为实验过程中所观察到的观察屏上干涉条纹的变化图.其中图2（a）表示未加玻璃板时，将可动镜臂M2移动到零光程差处可看到观察屏上一片光亮.图2（b）表示在可动镜臂M2前加入待测玻璃板后观察到的干涉条纹，干涉圆环的中心稍有偏离，由于动镜和定镜难以绝对垂直，中心的偏离无法避免.而图2（c）表示将M2向远离分束镜G1的一侧移动时看到的条纹先吞入然后到达吞吐转折点，这时干涉条纹是粗大、笔直的.

图2 观察屏上干涉条纹的变化图

此外，我们分别在动镜位置远大于零光程差位置和远小于零光程差位置（M2位于M1′远离分束镜的一侧）时，在动镜前加上玻璃板，让玻璃板仅挡住一半的光，到达动镜臂的光一部分经过玻璃板，一部分不经过玻璃板，两部分光分别与定镜臂的光干涉，在观察屏上可同时看到二者的干涉条纹，如下图3所示.图3（a）所示为动镜位置远大于零光程差处观察屏上二者的干涉条纹，左边较粗大的干涉条纹是加了玻璃板的，右边较密的干涉条纹是无玻璃板的.按照预想，对于图3（a）位置相比于未加玻璃板的一侧，加入玻璃板的一侧光程变大，故光程差增大，条纹应该变密.对于图3（b）位置相比于未加玻璃板的一侧，加入玻璃板的一侧光程变大，光程差减小，条纹应该变稀疏.而实际观察到的正好与预期相反.并且我们观察到当动镜由远离分束镜向靠近分束镜一侧移动的过程中，加了玻璃板的左边干涉条纹先到达吞吐转折点，而右边无玻璃板的后到达条纹吞吐转折点，即前者的吞吐转折点位于不加玻璃板的零光程差的外侧（远离分束镜的一侧）.理论上我们知道加入玻璃板使光程增大，新的零光程点应该位于原零光程点的内侧（靠近分束镜的一侧）.这说明了加入玻璃板后条纹吞吐转折点并不是零光程，对于非对称光路，不能通过条纹吞吐来判断零光程差的位置.加入玻璃板后的非对称光路中，条纹吞吐转折点和零光程差的位置是两个不同的概念，且二者分别位于不加玻璃板的零光程位置的两边.

图3 干涉圆环粗细疏密变化

实验中我们分别测量了未加玻璃和加入玻璃板后条纹吞吐转折点的位置 L1和 L2，具体数据如

表1所示，其中L1为未加玻璃板时的零光程差位置（即条纹吞吐转折点的位置），L2为加上玻璃板之后条纹吞吐转折点的位置.玻璃板的厚度测量数据如表2所示.按照前面的式（2），计算得玻璃板的折射率为n=ΔL/d+1=0.643＜1.这种异常现象说明加上玻璃板之后条纹吞吐转折处并不是零光程差位置.下面我们具体分析加入玻璃板后条纹吞吐转折点的物理意义，并且利用条纹吞吐转折点测量玻璃板的折射率.

表1 动镜M2位置记录表

表2 玻璃板厚度测量

3 干涉条纹吞吐机理的研究

图4所示为点光源的迈克耳孙干涉光路原理图［1］，它是通过分束镜将一束光分为两束，再将它们反射到一起，形成干涉图样.点光源S0通过分束镜成一虚像S，然后分别在两块反射镜M′1和M2上成像，即形成两个虚光源 S1和 S2，当两反射镜严格垂直时，这两个虚光源之间产生等倾干涉圆环图样.设M′1M2=t，则 S1S2=2t，对于中心亮条纹有 2t=kλ（λ为光源波长）.通过调节动镜 M2的位置来改变虚光源S2的位置，从而使得干涉圆环条纹发生吞入或者吐出的变化.理论上当动镜M2向靠近分束镜方向移动时，由于两虚光源 S1和 S2的间距变大，k增大，干涉条纹变纤细、紧密，表现为吐出现象.反之，如果动镜向远离分束镜方向移动，两虚光源S1和S2的间距变小，k减小，干涉条纹变粗大、稀疏，表现为吞入现象.

图4 点光源迈克耳孙干涉光路原理图

实验中，我们在动镜臂光路中加上玻璃板，该路光程增大，但并不意味着该路的虚光源移到了更远的地方.相反，因为玻璃板的折射作用，虚光源会向靠近动镜的方向移动.图5所示为在动镜M2前放上厚度为d、折射率为n的待测平板玻璃后，光在平板玻璃板内传播路径光路图.由于光在玻璃板内发生折射，折射光的反向延长线与主光轴的交点为新的虚光源S′，相对于未放玻璃板前的虚光源 S而言，光源被拉近了一段距离，这段距离的长度即为线段SS′的长度（等于 AB）.由于光线两次通过玻璃板，所以总共拉近的距离为2AB.

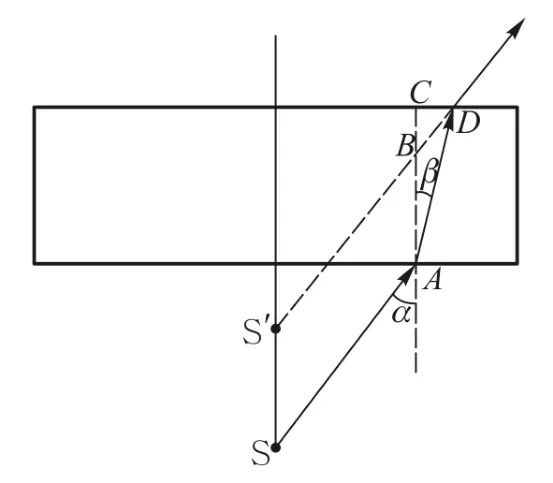
图5 光在玻璃板中的折射光路图

设虚光源S发出的光线的入射角为α，其相应的折射角为β，由几何关系易知

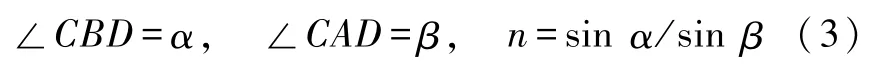
则

对应拉近的距离为

其中

因此，

考虑入射角α很小的情况，有［2］

图6所示为加入玻璃板的点光源干涉原理图.测量玻璃板折射率前先将动镜M2调到与M′1重合的位置，这时两臂光程差为零，虚光源S1与S2重合.在动镜前加上玻璃板之后，由于光源S两次经过玻璃板，等效为加入了厚度为2d的玻璃板.由于折射的原因，虚光源S移动到了S′处（SS′=2d（n-1）/n），相应的S2就移动到了 S′2的位置，此时 M2M′2=d（n-1）/n，S2S′2= 2d（n-1）/n.要使干涉条纹发生吞吐转折，就要通过移动动镜将虚光源S′2移动至与虚光源S1重合的地方，即将M2移动至M′2位置.在动镜移动的过程中，两光源之间距离一直减小，条纹一直是吞入的，直到S′2越过S1.

图6 加上玻璃板之后的点光源位置变化

而要使两臂重新回到零光程差，动镜的位置应该是M2″处，相应的虚光源S′2将移动到S2″，M2M2″= S2″S′2／2=（n-1）d.在动镜移动的过程中，两光源之间的距离不断增大，条纹不断吐出.新的零光程差位置M2″和条纹吞吐转折位置M′2分别位于原零光程差位置M2（M′1）（没有加玻璃板时）的两侧.这就是我们观察到异常现象的原因所在.

综上分析可知

即可得玻璃板折射率为

对于前面提到的干涉圆环粗细疏密的变化，用这种方法同样可以解释.

图7（a）所示为动镜位置远大于零光程差位置时的情况.加上玻璃板前，对于观察屏中心亮条纹有2S1S2=2t=k1λ.加上玻璃板之后，虚光源由S2移动到了S2′的位置，2S1S2′=2t-2d（1-1/n）=k2λ，可知k2＜k1，故而条纹变粗大、稀疏.同理可分析图 7（b）所示动镜位置远小于零光程差位置时的情况，得出加入玻璃板后观察屏上的条纹变密变细.加入玻璃板后通过移动动镜再次找到条纹吞吐转折点的位置L2处，此时动镜臂和定镜臂的光程差应该为

图7 条纹粗细疏密变化原理分析

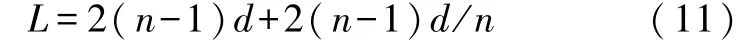
说明加入玻璃板确实增大了光程差，但是我们看到的条纹粗细疏密及条纹吞吐的变化不是简单的往外吐且条纹变密，条纹吞吐及粗细疏密的变化需要通过具体计算两臂的光程差随位置变化的关系来判断条纹吞吐，以及干涉角度随位置变化的关系来判断条纹粗细疏密的变化.

对于白光干涉的情况，由于白光的相干长度非常小，只有在零光程差附近时才能看到干涉条纹，并且白光是等厚干涉的直条纹，它并不依靠条纹吞吐转折来确定零光程差位置.所以用白光干涉法测量折射率并不会有所谓的异常现象.

4 实验测量玻璃板折射率

由前面的分析得出，通过分别测量不加玻璃板和加入玻璃板后条纹吞吐转折点处动镜所在的位置L1和L2，两者之差即为ΔL=｜L1-L2｜，通过测量玻璃板的厚度，即可推导出待测玻璃板的折射率.

由前面的公式（10）和表1、表2测得的数据计算可以得到，无机玻璃板的折射率为 n=1/（1+ΔL/

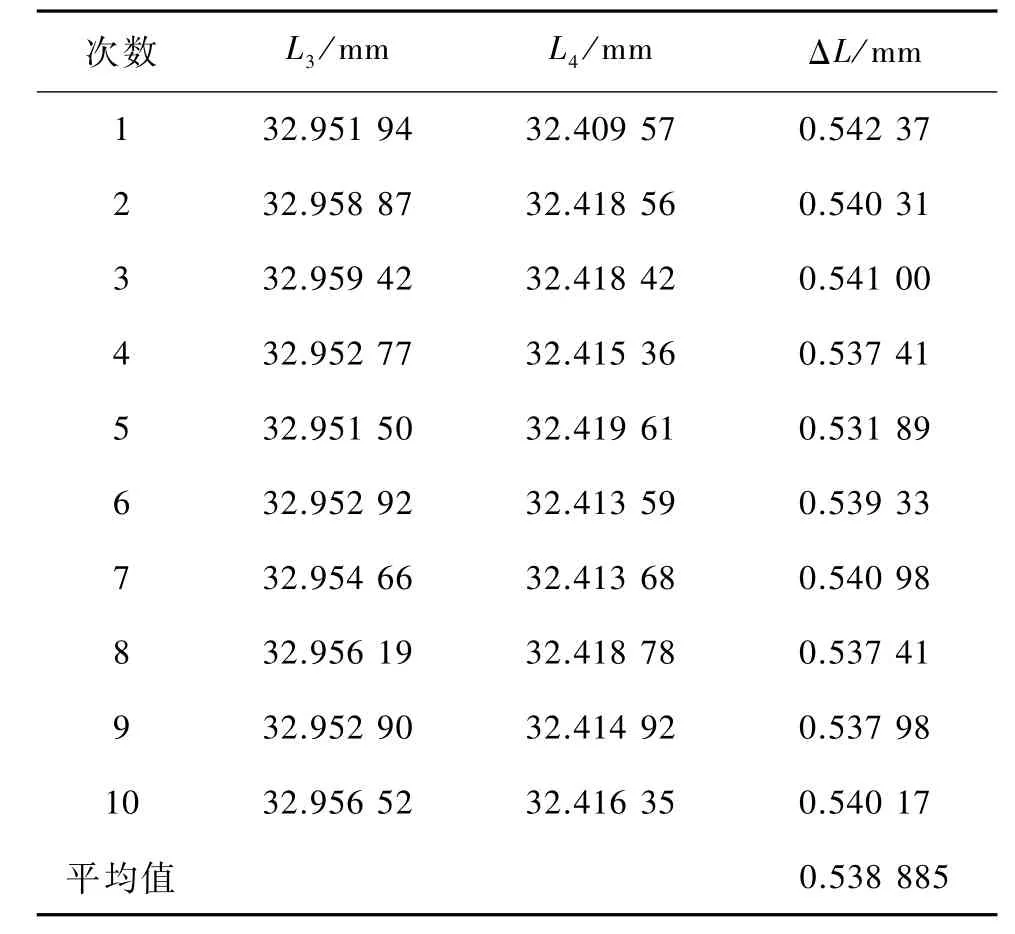
表3 白光干涉法测量折射率

则n=ΔL/d+1=1+0.538 885/0.993 6=1.542，激光干涉法测得的折射率相对于白光干涉法的误差为1.10%.可见上述分析是符合实际情况的，用激光干涉法测量折射率是可行的.

文献［2］中，作者将条纹吞吐的实质理解为干涉圆环角半径i随动镜位置x的变化，吞吐转折时，di/dx=0，并由此给出了吞吐转折点和零光程差位置的关系.而我们则是直接从几何光学出发给出了吞吐转折点与零光程差位置的关系式，方法简单直观，且从实验上进行了进一步的数据验证.

5 实验总结

未加上玻璃板之前，条纹吞吐转折就是零光程差位置，因为这个时候两条光路是对称的，产生干涉的两个虚光源可视为等效的光源，可直接比较它们之间的光程差.加上玻璃板之后，由于折射成像，就破坏了这种对称性，两个虚光源之间就不能直接比较光程差了.与此同时，笔者注意到补偿板的补偿作用的实质所在，它不仅在于补偿光程差，更在于使虚光源等效，而后者是靠动镜移动无法补偿的.若缺少补偿板，或者补偿板厚度不够、角度与分束镜不平行，都相当于在原本对称的光路基础上，再加上了一块玻璃板，就不能凭条纹吞吐来判断零光程差位置.

所谓的异常现象是因为理解不够深入，简单认为吞吐转折点就是零光程差的位置.对于上述现象的研究，有利于增加对迈克耳孙干涉和光的波粒二象性的理解，同时也得到了一种新的测量折射率的方法.这种方法的不足之处在于条纹吞吐转折判断存在一定主观因素的误差，优点在于激光相干长度大，测量方法简单，条纹便于观察.

致谢：衷心感谢国防科技大学的周艳丽老师和北京大学的穆良柱老师在实验中给予的帮助与有益讨论.

［1］ 李贤芳，李建青，马争争，等.基于点光源的迈克耳孙干涉实验条纹的机理分析［J］.物理与工程，2014，24（3）：37-41.

［2］ 雷前召.迈克尔逊干涉仪测量折射率的实验研究［J］.渭南师范学院学报，2011，26（10）：68-74.

The abnormal phenomenon of measuring refractive index with Michelson interferometer

NAN Yang1，XIONG Chang2，TANG Fang2，LI Chao-rong2
（1.School of Material Science and Engineering，Beihang University，Beijing 100191，China；2.School of Physics and Nuclear Energy Engineering，Beihang University，Beijing 100191，China）

While Michelson interferometer and laser are used to measure the refractive index of glass pane，there is an abnormal phenomenon.When we put a glass pane into one side of the light path，we observe an abnormal phenomenon of equal inclination inference rings puff.In this letter，we analyze the phenomenon in terms of geometrical optics and make clear the relationship between the turning point of interference fringe，zero light path difference and the relative location of virtual light sources.We also perform comparative analysis with experimental data.

Michelson interferometer；turning point of interference fringe；refractive index；geometrical optics；virtual light source

O 436.1

A

1000-0712（2016）11-0052-06

2015-12-30；

2016-05-04

北京航空航天大学重大教改项目资助

南阳（1994-），男，江西樟树市人，北京航空航天大学材料科学与工程学院2013级本科生.

熊畅，Email：xiongchang1821＠163.com