一种基于逻辑Petri网的过程挖掘方法
杜玉越,朱鸿儒,王 路,刘 伟
(山东科技大学山东省智慧矿山信息技术重点省级实验室,山东青岛 266590)
一种基于逻辑Petri网的过程挖掘方法
杜玉越,朱鸿儒,王 路,刘 伟
(山东科技大学山东省智慧矿山信息技术重点省级实验室,山东青岛 266590)
逻辑Petri网是抑制弧Petri网和高级Petri网的抽象和扩展,可在过程挖掘中简洁准确的表示活动之间复杂的业务逻辑关系.本文在传统Petri网挖掘方法的基础上,为了进一步提高复杂系统挖掘模型的简洁度和拟合度,尤其是对并行活动间存在复杂与或关系的系统,提出了一种基于逻辑Petri网的过程挖掘方法,并给出了逻辑Petri网中逻辑变迁的挖掘算法.它可以充分挖掘活动之间的业务逻辑,并且业务逻辑可用逻辑表达式表示.通过与相应Petri网模型的实例比较分析,例证了本文方法的正确性和有效性,且逻辑Petri网模型更加适合日志行为.
过程挖掘;Petri网;逻辑Petri网;逻辑变迁;挖掘算法
1 引言
过程挖掘通过挖掘实际的日志信息,发现并改进现实的模型[1],主要包括过程发掘、一致性检测和过程改进.在过程挖掘研究中,由于Petri网[2]描述和分析并发事件的优越性,许多研究都以Petri网作为描述过程的工具.α算法[3]是根据活动的顺序关系进行过程挖掘,当模型中不包括重复活动、不可见变迁以及特定结构式时,能挖掘得到系统的正确模型.由于α算法不能有效挖掘包括重复活动、不可见变迁和特定结构的系统模型,出现了α算法的多种扩展.针对α算法不能挖掘不可见变迁问题,文献[4]提出了可以有效挖掘不可见变迁的alpha#算法.针对α算法无法判定非自由选择结构问题,文献[5]提出了相应的过程挖掘方法.除α算法外,还有基于区域的过程挖掘算法[6,7].文献[6]从日志挖掘低等级的变迁系统,通过变迁系统得到模型,从而克服了α算法的一些局限性.为了进行多角度挖掘,出现了基于颜色Petri网CPN(Color Petri Net )的过程挖掘算法[7,8],并通过对Petri网进行拓展以考虑时间和成本对工作流决策的影响.这些方法通常以Petri网[9,10]为描述工具,但当并行活动之间的逻辑关系更加复杂时(如存在复杂的与或关系),仅使用Petri网不足以对其进行简洁地描述,且得到的模型不能充分反映日志信息.图1和图2是由相同旅游预订日志L1={σ1=t1t2t5,σ2=t1t2t4t5,σ3=t1t4t2t5,σ4=t1t4t2t3t5,σ5=t1t2t4t3t5,σ6=t1t2t3t4t5,σ7=t1t3t5}得到的Petri网模型,其中图1是使用α算法挖掘得到的Petri网模型,图2是由文献[7] 给出的先得到C-net后转化得到的Petri网模型.t1代表开始预订,t2代表预订机票,t3代表预订车票,t4代表预订旅馆,t5代表完成预定.黑方框代表不可见变迁,即在日志中没有对应的事件.预订机票(t2)和预订宾馆(t4)之间业务逻辑关系为:(1)预定机票t2可以单独发生;(2)在t2和t4同时发生时它们的关系是并行的.传统挖掘方法可能认为t2和t4是并行的,但忽视了t2可以单独发生的情况.此外,由图2知,在挖掘得到的Petri网模型中,需要添加大量的不可见变迁.
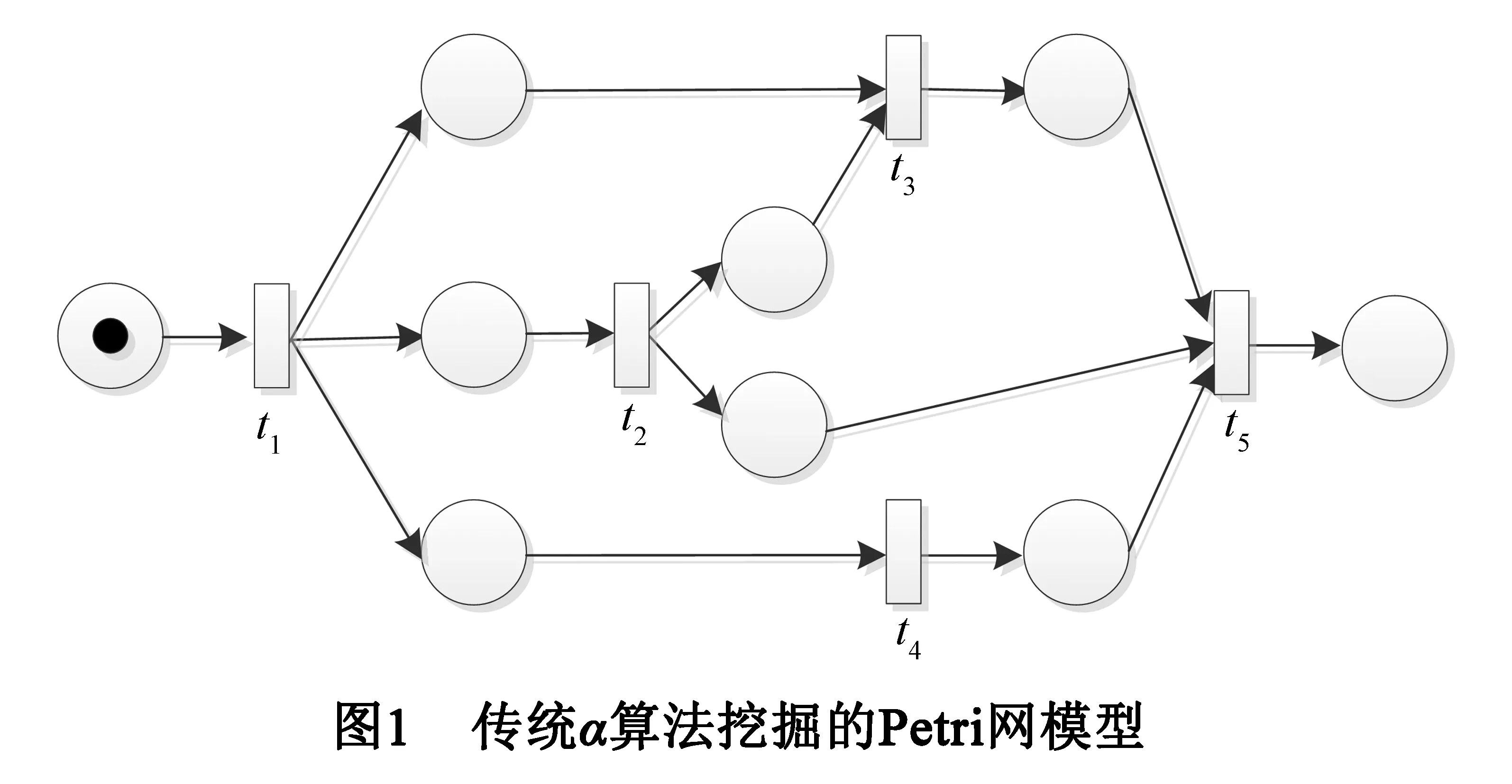
针对上述问题,有些学者提出先挖掘得到C-net模型,再将其转化成等价的Petri网模型,并使得到的模型比原有方法得到的模型更准确.为了得到更为简洁和更高拟合度的Petri网模型,本文采用另一种方法,在α算法挖掘结果的基础上,利用任务发生的频次关系得到活动之间的与或关系,通过活动之间的关系推导得到逻辑Petri网中的逻辑表达式,从而对挖掘模型进行约束,使得挖掘结果更加简洁、贴合日志,进而得到逻辑Petri网模型[11,12,13].同时,最后得到的逻辑Petri模型,也可以有效解决由α算法表示偏好(representational bias)引起的死锁问题.

2 基本概念
本节介绍逻辑真值与逻辑Petri网的相关概念.在逻辑Petri网中,通过逻辑表达式约束网中逻辑变迁的引发.为了讨论逻辑表达式的值,首先需要引入Petri网和逻辑真值的概念.
定义1 (Petri网)四元组PN=(P,T;F,M)称为一个Petri网PN,其中P是一个有限库所集,T是一个有限变迁集,F⊆(P×T)∪(T×P)是一个有限弧集,M:P→N称为网PN的一个标识.
有关Petri网更详细的定义请参见文献[2,9,10].
定义2 (逻辑真值)设f为库所集合P的逻辑表达式,M为P的标识向量,对∀p∈P,记p|M为在M下p的逻辑真值,记f|M为逻辑表达式f在M下的逻辑真值,f(p1,p2,…,pn)|M=f(p1|M,p2|M,…,pn|M) 其中p|M的值定义如下:
在定义2中,.T./.F.为逻辑值为真/假.下面给出逻辑Petri网的概念.
定义3 (逻辑Petri网)一个逻辑Petri网定义为一个六元组LPN=(P,T;F,I,O,M),其中
(1)P是一个有限库所集.
(2)T=TD∪TI∪TO是一个有限变迁集,T∩P=∅.若t∈TI∩TO,则·t∩t·=∅.
(a)TD表示Petri网中的变迁集;
(b)TI表示逻辑输入变迁集,对∀t∈TI,t的输入库所·t受逻辑表达式fI(t)的限制;
(c)TO表示逻辑输出变迁集,对∀t∈TO,t的输出库所t·受逻辑表达式fO(t)的限制;
(3)F=(P×T)∪(T×P)是一个有限弧集;
(4)I是由逻辑输入变迁到逻辑输入函数的映射,对于∀t∈TI,I(t)=fI(t);
(5)O是由逻辑输出变迁到逻辑输出函数的映射,对于∀t∈TO,O(t)=fO(t);
(6)M:P→Z0是Petri网的表示函数,Z0={0,1,2……};
(7)变迁引发规则:
(a)对∀t∈TD,变迁引发规则与传统Petri网一致.即设M[t>M′,M′(p)定义如下:
(b)∀t∈TI,若fI(t)|M=.T.,则逻辑输入变迁t可引发,记做M[t>M′,且对∀p∈·t,M′(p)=0;对∀pt·∪·t,M′(p)=M(p);对∀p∈t·,M′(p)=1;
(c)对∀t∈TO,若∀p∈·t,M(p)=1,则逻辑输出变迁t可引发,且对∀p∈·t,M′(p)=0;对∀p∈t·,需满足fO(t)|M′=.T.;对∀pt·∪·t,M′(p)=M(p).
图3给出了一个逻辑Petri网的例子.t1为逻辑输入变迁,I(t1)=(p1⊗p2)∧p3是t1的逻辑输入函数,(p1⊗p2)表示t1触发时,p1和p2中不能同时存在托肯.(p1⊗p2)∧p3表示t1在如下两种情况下满足触发条件:(1)p1和p3中存在托肯;(2)p2和p3中存在托肯.t2为经典Petri网的变迁,触发规则与经典Petri相同.t3为逻辑输出变迁,其逻辑输出函数O(t3)=p7∨p8表示t3引发后会有三种情况:(1)p7和p8中有托肯;(2)p7中有托肯;(3)p8中有托肯.

3 逻辑变迁的挖掘方法
本节给出逻辑变迁挖掘算法的相关定义以及算法描述.挖掘算法主要实现单个逻辑变迁的挖掘.由于逻辑输入变迁和逻辑输出变迁的相关结论可以通过逆网进行转化,因此本文仅给出挖掘逻辑输入变迁的挖掘方法.不同挖掘方法得到的Petri网模型可能不同,故将其转化为逻辑Petri网的方法也有所区别.因此,本文研究在α算法得到的Petri网模型基础上,通过进一步日志挖掘得到逻辑Petri网的方法.首先引入日志和迹的概念.
定义4 (迹,日志)PN=(P,T;F,M)为一个Petri网,日志L⊆T*,迹σ∈L.这里对于∀t⊆T,∃σ∈L,满足t∈&(σ),即L中记录了网中所有可以被记录的活动.用&(σ)表示由迹σ中所有活动构成的集合.
在挖掘到的Petri网模型中,若把变迁t转换为逻辑输入变迁,需要基于日志信息挖掘t与前面相邻变迁之间的逻辑关系.因此,下面引入前序变迁集的概念.
定义5 (前序变迁集)设PN=(P,T;F,M)为一个由日志L得到的Petri网,tk∈T,tk的前序变迁集定义为Tbef|tk={t|p∈·tk∧t∈·p}.

定义6 (变迁逻辑关系)设PN=(P,T;F,M)为一个由日志L得到的Petri网,tk∈T,tk的前序变迁集为Tbef|tk.L′为L在Tbef|tk投影得到的日志,σ为日志的一条迹,对T1,T2⊆Tbef|tk,(a>L′b)|σ表示在σ上活动a和b的关系为a>L′b.令A={σ|σ∈L′∧(a>L′b)|σ,a∈T1,b∈T2},B={σ|σ∈L′∧(b>L′a)|σ,a∈T1,b∈T2},C={σ|σ∈L′∧(a∈&(σ))},D={σ|σ∈L′∧(b∈&(σ))}.令k1=|A|/min{|C|,|D|},k2=|B|/min{|C|,|D|}.给定常数m和n用于度量变迁的并发程度,且0 在定义6中,a→b或b←a表示b依赖于a,∨表示或关系,∧表示与关系.k1和k2是介于0到1之间的数,用于描述变迁a和b的依赖关系.当k1接近于0时,表示在L′中极少出现a>L′b.当k1接近于1时,表示L′中a和b的关系为a→b.m和n是用于度量a和b的并发程度的数值.当lr(a,b)=a⊗b时,日志L′中极少出现a>L′b或b>L′a,即k1和k2都接近0.因此,这里记为k1+k2 定义6给出了前序变迁集中变迁的四种逻辑关系.在此基础上,可以进一步将前序变迁集中变迁的逻辑关系反映到其后继库所上,使库所的逻辑关系与变迁的逻辑关系保持一致. 定义7 (库所逻辑关系)设PN=(P,T;F,M)为一个由日志L得到的Petri网,t∈T,Tbef|t为t的前序变迁集.a,b∈Tbef|t,Pa={p|p∈a·∩·t},Pb={p|p∈b·∩·t},Pa-b=Pa-Pb,Pb-a=Pb-Pa.库所逻辑关系pl(lr(a,b))定义为: (1)若lr(a,b)=a∧b,则pl(lr(a,b))=f(Pa)∧f(Pb)=·T·即t触发时,在Tbef|t中a和b都触发; (2)若lr(a,b)=a⊗b,则pl(lr(a,b))=(f(Pa)∧┐f(Pb-a))∨(f(Pb)∧┐f(Pa-b))=.T.,即t触发时,在Tbef|t中a和b只有一个能触发; (3)若lr(a,b)=a∨b,则pl(lr(a,b))=f(Pa)∨f(Pb)=.T.,即t触发时,在Tbef|t中需要a或b触发; (4)若lr(a,b)=a→b,pl(lr(a,b))=(f(Pa)∧┐f(Pb))∨(f(Pb)∨┐f(Pa))=.T.,即t触发时,只有Pa或Pb中存在托肯. 在定义7中,当a⊗b时,Pa∩Pb≠∅,此时讨论的集合为Pa-b和Pb-a.日志L4={abc,ac}由α算法挖掘的Petri网模型如图4所示.但是,在该模型中,不能反映日志中的a→t.这个问题可在相应的逻辑Petri网中解决,且其优化后的逻辑Petri网模型如图5所示,其中I(t)=(f(Pa)∧┐(f(Pb)∨((f(Pb)∧┐f(Pa)).下面的定理1将证明若∀c∈Tbef|t,c≠a,则lr(c,b)≠c→b.即在Tbef|t中,只有a会与b存在依赖关系的情况下.Pa和Pb的逻辑关系pl(lr(a,b))=(f(Pa)∧┐f(Pb))∨(f(Pb)∧┐f(Pa)),即在处理a→b时,应将其视为a⊗b. 定理1 设LPN=(P,T;F,I,O,M)为一个由日志L得到的Petri网,t∈T,Tbef|t为t的前序变迁集,L′是L在Tbef|t上的投影,a,b∈Tbef|t且a,bTO.若a→b,且M[t>,则Pa与Pb的逻辑关系满足(f(Pa)∧┐f(Pb)∨(f(Pb)∧┐f(Pa))=.T.. 证明:先考虑不引入不可见变迁的情况,且Pa∈·b.采用反证法,令Pa·b,由a,b∈Tbef|t,a→b,则∃M[a>M′,(f(Pa)|M′)∧┐f(·b)|M′)=.T..令M′[b>M″,有(f(Pa)|M″)∧┐f(Pb)|M″)=.T..若t触发,则表达式应为(f(Pa)|M″)∧┐f(Pb)|M″),且原日志中不存在迹 因为Pa∈·b,故∀M,M[b>,f(Pb)|M=.T.,f(Pa)|M=.F.,且f(Pb)|M∧┐f(Pa)|M=.T..由a∈Ti|t1,故对∀M[a>M′,M′[t>,有f(Pb)|M′=.F.,f(Pa)|M′=.T.,且f(Pa)|M′∧┐f(Pb)|M′=.T..因此,逻辑输入变迁t的逻辑输入函数应为(f(Pa)∧┐f(Pb))∨(f(Pb)∧┐f(Pa)).[证毕] 由定理1,当a→b时,Pa和Pb的行为与a⊗b相同.故在下面处理a→b时,可把它作为a⊗b处理.从逻辑变迁的逻辑输入函数可知,两者是等价的. 定义7描述了逻辑输入变迁的前序库所逻辑与其前序变迁集中变迁逻辑之间的关系.由定义7和定理1,根据日志可得到逻辑变迁的逻辑输入表达式,再将逻辑关系转化成逻辑变迁的逻辑输入函数,可得到逻辑输入表达式I(t).为了得到逻辑变迁的逻辑输入函数,需要引入逻辑前序矩阵的概念. 定义8 (逻辑前序矩阵)PN=(P,T;F,M)是由日志L得到的Petri网,t1∈T,Tbef|t为t的逻辑前序变迁集.t的逻辑前序矩阵定义为(AI|t)[n][n](n=|Tbef|t|).设i,j∈[0,n),当i≠j时,(AI|t1)[i][j]=lr(i,j),反之,(AI|t1)[i][j]=∅. 由定义8,逻辑前序矩阵可表达前序变迁集中任意两个变迁的逻辑关系.对于给定的前序变迁集中的任意个变迁,通过逻辑前序矩阵可以得到这些变迁之间的逻辑关系.下面给出前序逻辑表达式的概念. 定义9 (前序变迁表达式)PN=(P,T;F,M)是由日志L得到的Petri网,t∈T,Tbef|t为t的逻辑前序变迁集,t的逻辑前序矩阵为(AI|t).对∀T′⊆Tbef|t,λ(T′,AI|t1)称为由AI|t得到的关于T′的前序变迁表达式. 基于逻辑前序矩阵挖掘前序变迁集中变迁的逻辑关系时,要考虑⊗和∧,以及⊗和∨是否满足分配律.如a,b,c∈Tbef|t1,lr(a,b)=a∧b,lr(a,c)=a∧c,lr(b,c)=b⊗c,若先挖掘得到⊗,可得到表达式f1=a∧(b⊗c);若先挖掘得到∧,可得到表达式f2=(a∧b)⊗(a∧c).但是,下面将证明这两种顺序是等价的,即∧对⊗满足分配率.这里证明plf1(lr(a,lr(b,c)))=plf2(lr(a,c),lr(a,b)),其中plf1(lr(a,b))表示在变迁表达式f1下得到的库所逻辑表达式. 定理2 设PN=(P,T;F,M)为一个由日志L得到的Petri网,t∈T,Tbef|t为t的前序输入变迁集,a,b,c∈Tbef|t.若lr(a,b)=a∧b,lr(a,c)=a∧c,且lr(b,c)=b⊗c,则对于逻辑表达式f1=a∧(b⊗c)与f2=(a∧b)⊗(a∧c),有plf1(lr(a,lr(b,c)))=plf2(lr(a,c),lr(a,b)). 证明:由定义6,左边=plf1(lr(a,lr(b,c)))=f(pa)∧f(pb,c)=f(pa)∧((f(Pc)∧┐f(Pb-c))∨(f(Pb)∧┐f(Pc-b)))=((f(pa)∧f(Pc)∧┐f(Pb-c))∨(f(pa)∧f(Pb)∧┐f(Pc-b)).右边=plf2(lr(a,c),lr(a,b))=(f(pa,c)∧┐f(p(a,b)-(a,c))∨(f(pa,b)∧┐f(p(a,c)-(a,b)))=((f(pa)∧f(Pc)∧┐f(Pb-c))∨(f(pa)∧f(Pb)∧┐f(Pc-b))=plf1(lr(a,lr(b,c))). 因此,左边=右边,即原等式成立.[证毕] 类似的还可以得到⊗对∧也满足分配率,即⊗和∧都满足分配率.同样可以推出⊗和∨也满足分配率.在Petri网中给出一个变迁t的逻辑前序矩阵AI|t,根据定理2,下面将给出前序变迁集中变迁逻辑关系的挖掘算法. 定义10 (逻辑输入函数)设LPN=(P,T;F,I,O,M)是由日志L得到的逻辑Petri网,t∈T,Tbef|t为t的逻辑前序变迁集,λ为由矩阵AI|t得到的逻辑表达式.t的逻辑输入函数定义为fI(t)=pl(λ). 定义10给出了逻辑表达式与逻辑输入函数的关系,下面的算法1将实现由前序变迁矩阵挖掘出前序变迁集中变迁的逻辑关系. 在算法1中,为了处理‘→’与‘∧’,下面分别给出相应的转换规则. 规则1 (a→b的转换规则)LPN=(P,T;F,I,O,M)为一个由日志L得到的逻辑Petri网,t∈T,Tbef|t1为t的前序输入变迁集.a,b∈Tbef|t,若a→b且aTO,根据定理1,使a·∩·b=pa,即合并a·∩·b与pa.在AI|t中把lr(a,b)置为⊗.若a∈TO,则只在AI|t中将lr(a,b)置为⊗. 对于规则1,虽然在逻辑输出变迁中也可以得到类似规则,但变迁a和b在相邻的逻辑输入变迁和逻辑输出变迁之间时,可能会导致同样的结构被处理两次.为了避免这个问题,规定同一个a→b结构只能被处理一次,且在其他变迁中记a→b为a⊗b. 规则2 (a⊗b的转换规则)LPN=(P,T;F,I,O,M)为一个由日志L得到的逻辑Petri网,t∈T,Tbef|t为t的输入变迁集.a,b∈Tbef|t且a,bTO.pl(a⊗b)=(f(pa)∧┐f(pb-a))∨(f(pb)∧┐f(pa-b)),其中 (1)当pa∩pb=∅时,pl(a⊗b)=f(pa)⊗f(pb); (2)当pb=pa时,pl(a⊗b)=f(pa)∨f(pb)=f(pa); (3)当pb≠pa和pb-pa=∅,即pl(a⊗b)=f(pa)∨(f(pb)∧f(pa-b))时,F=F-a×(pa∩pb),pa=pa-pb,且pl(a⊗b)=(f(pa)∧┐f(pb))∨(f(pb)∧┐f(pa)); 规则2给出了化简逻辑Petri网模型和逻辑表达式的方法.如在图1中,pl(t1,t4)=(f(pt1)∧┐f(pt4-t1))∧(f(pt4)∧┐f(pt1-t4)).因为pt1-t4=∅,故F=F-a×(pt1∩pt4),pt4=pt4-pt1=p2,且pl(t1,t4)=p1⊗p2.这样就能利用引入的逻辑表达式简化逻辑Petri网模型.将挖掘得到的模型转化成它的逆网,可以得到逻辑输出变迁的类似定义. 在执行算法1时,利用规则1和规则2可以改善原有挖掘结果.在处理t1⊗t2中第三种情况时,将出现库所的消减.算法1没有考虑(的优化顺序,这会影响最终得到的逻辑Petri网的挖掘效果.图6是由L4={〈t1,t3,t5,t7〉2,〈t1,t5,t3,t7〉3,〈t2,t4,t6,t7〉2,〈t2,t6,t4,t7〉4}挖掘得到的Petri网.若将t7视为逻辑输入变迁,图7给出了其逻辑前序矩阵.使用算法1,首先寻找AI|t7中为⊗的元素,有λ1=t3⊗t4,λ2=t3⊗t6,λ3=t4⊗t5,且λ4=t5⊗t6.根据t3∧t5,得λ1=λ1∧λ3=t4⊗(t3∧t5),λ2=λ2∧λ4=t6⊗(t3∧t5).由t4∧t6,得λ1=λ1∧λ2=(t3∧t5)⊗(t4∧t6).此时,得到如图8所示的逻辑Petri网模型,且根据t3∧t5得λ1=λ1∧λ4=(t3⊗t4)∧(t5⊗t6).λ2=λ2∧λ3=(t3⊗t6)∧(t4⊗t5).λ1=λ1∧λ2=(t3⊗t4)∧(t5⊗t6)∧(t3⊗t6)∧(t4⊗t5)=(t3∧t5)⊗(t4∧t6).因此,得到如图9所示的逻辑Petri网模型. 图8和图9的前序变迁表达式相同,但最后的逻辑输入表达式以及逻辑Petri网模型不同.图8中出现了一次规则2中的第(4)种情况,而图9中出现了两次这种情况.由于第(4)种情况涉及到库所的消减,因此,图9的库所和弧比图8的都更少.为了使得到的逻辑Petri网模型尽量简洁,在处理⊗时,采用贪心算法.优先处理出度较多的变迁,且在处理时优处理规则2中的第(4)种情况.因此,可以得到改进后的算法2. 由算法2,可以确定前序变迁集中变迁之间的逻辑关系.在图1中,{t2,t3,t4}通过算法2可以得到(t2∧t4)⊗(t3∧t4),代表迹σ∈{t1t2t3t4t5,t1t4t2t3t5,t1t2t4t3t5}.但此时无法表示t2与t3单独发生的情况.为了解决这个问题,算法3将日志在前序变迁集上进行投影.将投影后长度相同的迹分为一组,并将每组中的变迁用算法2得到其逻辑关系.这样就可以得到能反映日志的前序变迁表达式,进而计算相应的逻辑输入函数. 本节给出了一种单个逻辑输入变迁的挖掘方法.在此基础上,按优化所有路由选择变迁得到的逻辑Petri网模型,比原有Petri网模型能更充分反映日志中的信息.而优化的顺序不同会引起最终结果的不同,这会在下面的例子中给与展示. 本节给出第3节挖掘方法的实例分析,从而展示以逻辑Petri网挖掘模型比Petri网挖掘模型更符合日志行为.以某三甲医院实际就诊日志为例,给出其逻辑Petri网挖掘模型与相应Petri网挖掘模型的比较分析,其中Petri网模型是由启发式(Heuristic)算法得到的模型转化而来的. 例1 本例中的日志和图1中的日志轨迹相同,L1={σ1=t1t2t5,σ2=t1t2t4t5,σ3=t1t4t2t5,σ4=t1t4t2t3t5,σ5=t1t2t4t3t5,σ6=t1t2t3t4t5,σ7=t1t3t5}.首先将t5转换为逻辑输入变迁:由模型可知Ti|t5={t2,t3,t4},由定义6,可得到日志并发度k(t2,t3)=0.6,k(t3,t2)=0,k(t2,t4)=0.25,k(t4,t2)=0.25,k(t3,t4)=0.25,k(t4,t3)=0.25.取m=0.3,n=0.5,则lr(t2,t3)=t2→t3,lr(t2,t4)=t2∧t4,lr(t3,t4)=t3∧t4. 构建逻辑前序矩阵AI|t5如下: 根据上述三个逻辑前序矩阵,依次得到λ1=t1⊗t2,λ2=t2∧t4,λ3=t2∧t4,λ4=(t2⊗t3)∧t4,且λ=(t2⊗t3)∨(t2∧t4)∨((t2⊗t3)∧t4).根据相应转换规则,合并pt2与·t3得到图10中的逻辑Petri网.根据定义7,I(t5)=pl(λ)=(p3⊗p4)∨(p3∧p5)∨(p3⊗p4)∧p5)=(p3⊗p4)∨((p3⊗p4)∧p5).将t3转化为逻辑输入变迁时,由于t3的前序变迁集为{t1,t2},且lr(t1,t2)=t1→t2,则合并pt1与·t2后,有I(t3)=p1⊗p3.处理t1时,由于t2→t3在处理t5时已被处理,记lr(t2,t3)=t2⊗t3,得O(t1)=p1∨(p1∧p2). 若处理变迁t1t2t5,可以得到图11中的逻辑Petri网模型.在图11中,O(t1)=(p1⊗p3)∨((p1⊗p3)∧p2),O(t2)=p3⊗p4,I(t5)=p4∨(p4∧p5).图11中的模型可正确反映原日志中的模型.依次处理变迁t3t1t5和t3t5t1可以得到和图10相同的逻辑Petri网,依次处理t2t1t5和t2t5t1可以得到和图11相同的逻辑Petri网模型.对比图1和图10,日志L1在图1中只有σ4,σ5,σ6重演,而日志L1在图11中的迹均可以被重演.因此,挖掘得到的逻辑Petri网模型相比原Petri网模型,能更加充分的反映日志中的信息.对比图2和图10,两者均可以重演日志L1中的迹,但通过比较比较库所和变迁的数目可以发现图10中的模型更为简洁. 例2:图12给定某三甲医院门诊服务和检查的部分流程.图13为图12中t11代表的子流程,包括6520条迹,以及九个事件:挂号、PET-CT、普通CT、胸部增强CT、生化全套、血沉、血气分析、血常规和诊断,在将其进行格式转化成为XES文件后,基于该日志,在ProM6.5下用ProM中启发式算法挖掘得到的Petri网模型,如图13所示,其中黑方框表示不可见变迁.可见变迁中左边第一列变迁名为“挂号”,第二列从上到下变迁名分别为“PET-CT”、“胸部增强CT”和“普通CT”,第三列从上到下变迁名分别为“生化全套”、“血沉”、“血气分析”和“血常规”,第四列变迁名为“诊断”.在ProM上使用α算法挖掘得到的Petri网,如图14所示.在图14的基础上,利用本文方法进一步挖掘日志信息,得到的逻辑Petri网如图15所示,其中“挂号”为逻辑输出变迁,且其逻辑输出表达式为Oregister=p1⊗p3.“诊断”为逻辑输入变迁,且其逻辑输入表达式为Idiagnose=p3⊗p4(p6.表1对由Heuristic-net得到的Petri网、α算法挖掘 得到的Petri网、C-net网及相应的逻辑Petri网的性能指标,进行了比较分析.由表1可知,图13和图15的拟合度(Fitness)比图14中的模型要好,图14和图15比图13的模型规模更小,且主要体现在库所的规模以及不可见变迁的数量上.从泛化度(Generalization)以及精确度(precision)[14]上比较,图15的模型比图13的好. 在时间消耗上,α算法和启发式算法挖掘Heuristic网挖掘效率最快,这是因为它们在大规模日志上没有重复的操作,如表1所示.本文方法需要在α算法的基础上,还需通过日志得到定义6中相应的频次关系.因此,本文方法在时间上的花费会比前两种算法要高.图16为通过启发式算法挖掘得到C-net后,在ProM下得到的BPMN模型(可转化为与图15等价的逻辑Petri网).挖掘C-net需要多次遍历日志[1],如对于图1中的变迁t1,本文方法需要确定{t2,t3},{t3,t4}和{t2,t4}三组变迁之前的频次关系,而挖掘它的C-net需确定所有可能的绑定关系,即{t1,t2},{t1,t3},{t1,t4},{t1,{t2,t3}},{t1,{t3,t4}),{t1,{t2,t3}},{t1,{t2,t4}},{t1,{t2,t3,t4}}.由表1知,C-net的平均时间比本文逻辑Petri网花费时间更多.C-net中没有库所和变迁的概念. 表1 例2中四种模型的比较 库所变迁拟合度泛化度精确度平均时间消耗(s)Heuristic-net18540.96350.80210.85110.6795Petri网890.78790.83500.81250.5683C-net0.97680.90660.93327.8626逻辑Petri网790.99980.93780.93633.5039 本文针对复杂系统的过程挖掘问题,特别是对于系统中在并行活动之间存在复杂与或关系的过程挖掘,将逻辑Petri网应用到过程发掘中,在原有α算法的基础上,考虑事件的频次,提出了一种逻辑变迁的挖掘方法.挖掘得到的逻辑Petri网模型能够正确描述活动之间复杂的业务逻辑关系.本文方法可以作为α及其拓展方法的补充,即在原有方法需要更加深入的挖掘日志信息时,可将逻辑Petri作为工具进行更深入的挖掘.因此,本文方法的效率会低于一般的α算法或扩展的α算法,比如alpha#算法[4].算法效率的提高及批量日志的自动挖掘与比较,将作为下一步的研究内容. [1]Van der Aalst W.Process Mining:Discovery,Conformance and Enhancement of Business Processes[M].Berlin Heidelberg:Springer,2011.1-30. [2]杜玉越,薛洁,李彦成.基于服务簇的服务组合替换与分析[J].电子学报,2014,42(11):2231-2238. Du Yuyue,Xue Jie,Li Yancheng.Substitution and analysis of service composition based on service clusters[J].Acta Electronica Sinica,2014,42(11):2231-2238.(in Chinese) [3]Van der Aalst W,et al.Workflow mining:discovering process models from event logs[J].Knowledge and Data Engineering,IEEE Transactions on,2004,16(9):1128-1142. [4]Wen L,Wang J,van der Aalst W M P,et al.Mining process models with prime invisible tasks[J].Data & Knowledge Engineering,2010,69(10):999-1021. [5]Wen L,van der Aalst W M P,Wang J,et al.Mining process models with non-free-choice constructs[J].Data Mining and Knowledge Discovery,2007,15(2):145-180. [6]Van der Aalst W,et al.Process mining:a two-step approach to balance between underfitting and overfitting[J].Software & Systems Modeling,2010,9(1):87-111. [7]Busi N,Pinna G,van der Aalst W.An Iterative Algorithm for Applying the Theory of Regions in Process Mining[M].Beta,Research School for Operations Management and Logistics,2007.16-38. [8]Rozinat A,Mans R S,Song M,et al.Discovering colored Petri nets from event logs[J].International Journal on Software Tools for Technology Transfer,2008,10(1):57-74. [9]Du Y Y,Jiang C J.On the design and temporal Petri net verification of grid commerce architecture[J].Chinese Journal of Electronics,2008,17(2):247-251. [10]梅晓勇,李师贤,等.一种支持组合事务的执行语义分析方法[J].电子学报,2012,40(7):1386-1396. Mei Xiaoyong,Li Shixian,et al.An execution semantic analysis method for composition transaction[J].Acta Electronica Sinica,2012,40(7):1386-1396.(in Chinese) [11]Du Y Y,Qi L,Zhou M C.Analysis and application of logical Petri nets to e-Commerce systems [J].Systems,Man,and Cybernetics:Systems,IEEE Transactions on,2014,44(4):468-481. [12]Du Y Y,Jiang C J,Zhou M C.A Petri Net-based model for verification of obligations and accountability in cooperative systems[J].IEEE Transactions on Systems,Man,and Cybernetics--Part A:Systems and Humans,2009,39(2):299-308. [13]Du Y Y,Ning Y H,Qi L.Reachability analysis of logic Petri nets using incidence matrix[J].Enterprise Information Systems,2014,8(6):630-647. [14]Van der Aalst W,Adriansyah A,van Dongen B.Replaying history on process models for conformance checking and performance analysis[J].Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery,2012,2(2):182-192. 杜玉越 男,1960年生于山东聊城.博士,教授,博士生导师.研究方向为过程挖掘、工作流技术、Petri网应用等. E-mail:yydu001@163.com 朱鸿儒 男,1991年生于山东淄博.硕士研究生.研究方向为过程挖掘、工作流、Petri网. Email:zhr20122013@163.com A Method of Process Mining Based on Logic Petri Nets DU Yu-yue,ZHU Hong-ru,WANG Lu,LIU Wei (KeyLaboratoryforWisdomMineInformationTechnologyofShandongProvince,ShandongUniversityofScienceandTechnology,Qingdao,Shandong266590,China) Logic Petri nets are the abstraction and extension of the Petri nets with inhibitor arcs and high level Petri nets,and can describe the Business Logic among activities concisely and accurately in process mining.To further improve the simplicity and fitness of the mining models of complex systems,especially the systems with the complex AND-OR relation in parallel activities,a method of process mining is proposed based on Logic Petri nets to improve Petri net models in this paper.An algorithm of mining logic transitions is presented to transform the business logic among activities in event logs into logic expressions adequately.Experiment results illustrate that the mining logic Petri nets can represent the event logs more properly and succinctly than the corresponding Petri nets. process mining;Petri net;logic Petri net;logic transition;mining algorithm 2015-06-08; 2015-12-28;责任编辑:蓝红杰 国家自然科学基金(No.61170078,No.61472228);山东省泰山学者建设工程专项经费;山东省自然科学基金(No.ZR2014FM009);青岛市科技计划基础研究项目(No.13-1-4-116-jch);山东省优秀中青年科学家科研奖励基金(No.BS2015DX010) TP311 A 0372-2112 (2016)11-2742-10 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.11.025






4 实例分析



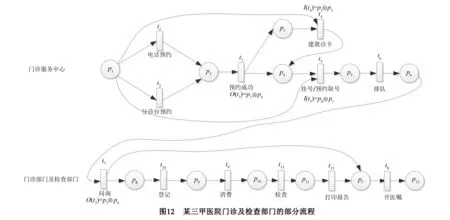





5 总结



