电子系统电磁脉冲易损性评估的分层贝叶斯网络模型

刘 钰,韩 峰,陆希成,王建国,2

(1.西北核技术研究所第五研究室,陕西西安 710024；2.西安交通大学电子与信息工程学院,陕西西安 710049)



电子系统电磁脉冲易损性评估的分层贝叶斯网络模型

刘 钰1,韩 峰1,陆希成1,王建国1,2

(1.西北核技术研究所第五研究室,陕西西安 710024；2.西安交通大学电子与信息工程学院,陕西西安 710049)

针对电子系统电磁脉冲易损性评估问题,提出了基于分层贝叶斯网络的电子系统电磁脉冲易损性评估模型建模方法.分析了电子系统分层结构特征及其电磁脉冲效应的特点,应用电磁拓扑理论中的相互作用顺序图分析系统电磁耦合途径,确定系统内底层屏蔽区域节点,研究了相互作用顺序图与系统分层贝叶斯网络的拓扑关联关系,在系统分层贝叶斯网络模型中增加底层屏蔽区域节点层,从而建立系统易损性评估模型,并给出了相应的建模步骤.最后以某电子机械传动系统电磁脉冲易损性评估问题为例说明了建模和计算过程.

电磁脉冲；敏感性；易损性；可靠性；电子系统；分层贝叶斯网络；评估模型

1 引言

电子系统一般是由多个电子分系统和单元电路组合而成的复杂系统,具有典型的分层系统(Hierarchical System,HS)特征,系统结构具有层次性,系统各层都拥有独立可分离的模块或部件[1],且在系统各部件中都使用了大量半导体器件及非金属材料(对电磁脉冲没有屏蔽能力).随着半导体器件结构日趋复杂,其工作电压越来越低,工作频率越来越高,导致电子系统对电磁脉冲扰乱与损伤效应的敏感程度大幅度增加,电磁脉冲对电子设备产生效应的阈值不断降低,电磁脉冲辐射场已对现代电子设备的安全运行构成了一定的威胁[2～4].

国内外的研究人员开展了大量的电子系统电磁脉冲效应的研究工作[5～8].实验方法是研究电子系统电磁脉冲效应的主要手段,针对系统的分层特征,可分别开展器件级、子系统级和系统级的电磁脉冲效应实验研究.通过实验方法可以较为准确的获取系统各层元素的效应阈值,具有较高的实用价值.但实验研究受限于实验条件及实验成本,一些昂贵的电子系统或单元器件的效应实验,实验次数十分有限,而电磁脉冲与电子系统相互作用受多种因素影响,无法通过少量实验研究各参数条件下的系统效应,实验结论一般不具备很强的外推性[4].

与实验方法相对应,电子系统核电磁脉冲易损性评估也需要分层次进行.一般来说,如果系统中所有的耦合机制和相互作用关系都清楚,那么一个系统的易损性评估就可以通过综合所有相关的子系统以及各器件(组件)的易损性评估结论来完成.然而,构成完整电子学系统的子系统以及各器件(组件)相对独立又互相配合,各子系统之间及它们与整系统之间的相互关系、耦合机制都十分复杂.子系统是否安置在系统之中,其所处防护屏蔽环境亦不同,系统功能的实现与子系统的放置位置和工作模式都密切相关,即使获得了单独子系统的敏感度数据,最终也必须综合系统耦合通道情况与系统运行模式才能分析获取子系统实际的效应数据.系统的易损性评估模型也应考虑系统耦合通道情况与系统运行模式的共同影响[4].另外,在以往的效应实验研究工作中,多数采用了确定性的分析方法,但在电磁脉冲与电子系统相互作用的过程中存在大量的不确定性.因此,有研究人员研究了以不确定性分析方法为基础的电子系统电磁脉冲易损性评估方法.在文献[9～11]中提出了基于故障树分析(Fault Tree Analysis,FTA)的电子系统电磁脉冲易损性评估方法.

FTA方法是一种用于大型复杂系统可靠性和安全性分析的方法,在航空、核能和机械等领域得到了广泛应用.但FTA方法也存在一些不足,对于复杂系统的功能建模,由于基本事件较多导致基于最小割集布尔运算的计算十分复杂.基本事件还需要满足独立性条件[12],但随着系统规模的增大,其状态空间呈指数增长,求解较为困难.而贝叶斯网络(Bayesian Networks,BN)是一种基于概率论和图论的不确定知识的表示模型[13],具有较强的建模能力并且能够克服故障树分析方法的不足,近年来逐渐被应用于复杂系统的可靠性和安全性分析[14～16].特别文献[17]中提出了系统的分层贝叶斯网络(Hierarchical Bayesian Networks,HBN)建模方法,能够描述分层系统内元素失效的相关性,并研究了系统各层元素可靠性信息的信息融合算法,能够显著提高系统可靠性评估结果的准确性.

本文基于电子系统电磁脉冲效应特点,并结合电子系统的分层特征,应用电磁拓扑理论中的相互作用顺序图对系统电磁耦合途径进行分析,确定系统内底层屏蔽区域节点.研究了相互作用顺序图与系统HBN的拓扑关联关系,以系统底层屏蔽区域作为根节点对系统HBN模型进行了重构,从而建立系统易损性评估模型,并给出了相应的建模步骤.最后以某电子机械传动系统电磁脉冲易损性评估问题为例说明了建模计算过程.

2 分层贝叶斯网络

一般,BN由节点{X1,…,Xn}和节点(node)之间的弧(arc)构成[18].每个节点Xi都是一个随机变量.如果存在自Xi指向Xj的弧,则称Xi为Xj的父节点.每一个节点都可能存在或不存在父节点.弧描述了节点与其父节点之间条件概率关系.

而表示分层系统的HBN功能逻辑需要一些特殊的标记,节点记作X(l,m),l表示系统层级,l=1,2,…,L,m表示l层某元素,m=1,2,…,Ml.所以,X(l,m)表示的是第l层的第m个节点.HBN还有几个约束条件：(1)若l1表示上层,而l2表示下层,则不允许存在l1指向l2的弧,即某节点的失效可由其父节点失效导致,但反之不成立；(2)不允许存在非相邻层级节点间的弧,是指节点的失效不能越层传递,必须通过其子节点将失效信息传递下去；(3)同层节点之间的弧表示层级内级联失效.HBN的拓扑结构如图1所示.

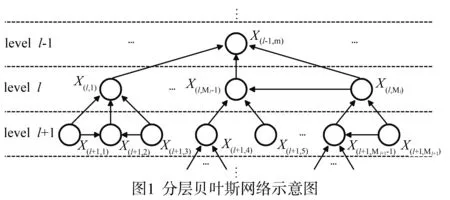
用Pa(X(l,m))表示X(l,m)父节点集合,显然Pa(X(l,m))可包含X(l,m)的同层节点或l+1层的节点.Pr(X(l,m)|Pa(X(l,m)))表示X(l,m)在给定其父节点集合时的条件概率.由于节点取值为离散值,故该变量常使用条件概率表(Conditional Probability Table,CPT)描述.而X(l,m)的及其非空父节点的联合概率表示为[18]

Pr(X(l,m),Pa(X(l,m)))=Pr(X(l,m)|Pa(X(l,m)))

·Pr(Pa(X(l,m)))

(1)

基于式(1),Pr(Pa(X(l,m)))又可递归分解.一旦获得其联合概率,则任一节点的边际概率为

(2)

根据父节点的位置,可将CPTs分为层级内CPTs和层级间CPTs两类.Pr(X(l,m)|Pa1(X(l,m)))表示层级间CPTs,Pa1(X(l,m))表示节点X(l,m)位于l+1层的父节点集合；Pr(X(l,m)|Pa2(X(l,m)))表示层级内CPTs,Pa2(X(l,m))表示节点X(l,m)的同层父节点集合.CPTs一般由专家知识或可靠性试验数据获得.

3 电子系统电磁脉冲易损性评估模型

3.1 系统定性电磁拓扑分析

电磁脉冲作用于电子系统具有由外向内、由表及里的特点.其效应作用主要表现为脉冲依靠前门或后门耦合,进入电子设备系统内部,在金属表面或金属导线上产生感应电流、电压,或对半导体介质加热导致局部升温,造成电路器件状态反常,器件性能下降,甚至使半导体器件、微波器件被损伤、烧毁等,从而破坏电子系统的正常功能[4].

为了描述电磁脉冲与电子系统相互作用,Baum在上世纪七十年代提出了电磁拓扑理论(Electromagnetics Topology,EMT )[19～21].EMT理论提出了良好屏蔽近似(Good Shielding Approximation,GSA)原则,GSA假设外部区域对内部区域的作用不可以忽略,而内部区域对外部区域的影响可以忽略[22].从而可以把系统的结构分解成相互包含的不同子区域,这些子区域相互独立,仅通过特定途径(如孔缝,导线,电缆)相互作用.电磁拓扑方法通过拓扑图(Topology Diagram,TD)和相互作用顺序图[23](Interaction Sequence Diagram,ISD)定性地描述电磁脉冲激励信号在电子系统内部的传输路径.

为了描述系统的EMT结构,每一个面可用唯一的标示符来区别,记作S(l,m),l=1,2,…,L表示屏蔽层序列,m=1,2,…,Ml表示系统屏蔽第l层的第m个屏蔽面,最外层表面表示为S(1,1),每个面S(l,m)把两个区域分开,这些面把系统分离成许多区域,对应于V(l,m),l=0,1,…,L表示屏蔽层划分的区域序列,m=0,1,…,Ml表示第l区域的第m个子区域,系统外部包含源的区域为V(0,0).显然,这种标记电磁屏蔽拓扑结构的方法,是根据屏蔽面对系统层次结构顺序进行标记的.复杂系统内任一子区域都可以通过S(l,m)和V(l,m)来表示,这种用屏蔽面和相应的子区域表示电子系统电磁屏蔽的图为拓扑图,如图2所示.

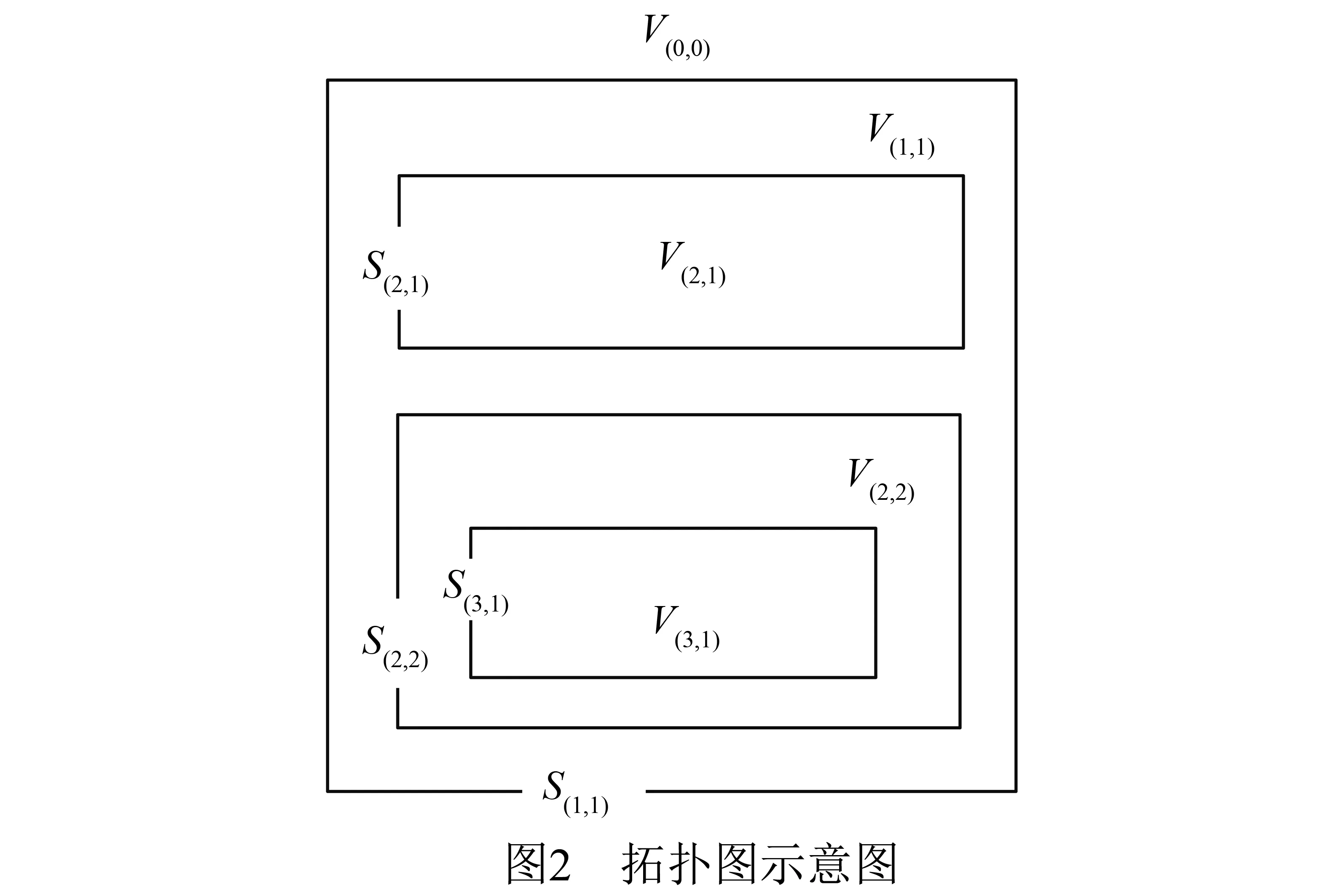
在GSA下,能量从上一个屏蔽层到下一个屏蔽层是单向传输的.相互作用顺序图用来表示电磁干扰的途径和能量的流向.它由节点(node)和边(edge)组成.图2对应的相互作用如图3所示.节点分为区域节点(volume node)和面节点(surface node).区域节点相应于某个区域空间内的点,由实心圆表示.在一个区域内可以存在几个区域节点,用来表示区域内需要分析的不同位置.面节点表示位于屏蔽面上的节点,由空心圆表示.同样,一个屏蔽层上可以有多个面节点,表示不同的能量耦合途径.

3.2 易损性评估模型的建立方法

电子系统的HBN模型与系统电磁相互作用顺序图具有相似的分层特征.相互作用顺序图中电磁应力(Electromagnetic Stress,EMS)由上至下,自系统外区域,经系统各层屏蔽面,向各单元部件所在区域传递；而在HBN中,可靠性信息自下而上,由代表单元部件的根节点经过HBN各层向系统节点传递.若将系统按系统、子系统和单元部件三个层级分解,根据电磁拓扑理论,系统各层元素都处于相应的各层屏蔽区域内.

假设①系统各屏蔽层均满足GSA；②系统的单元部件处于系统底层屏蔽区域内；③各底层屏蔽区域均包含且仅包含一个单元部件,即系统各单元部件都具有独立的屏蔽结构.在这样的假设前提下,底层屏蔽区域与系统单元部件之间存在一一对应的包含关系,基于这种包含关系可融合系统可靠性信息与系统单元部件电磁脉冲易损性信息,从而建立系统电磁脉冲易损性评估模型.

在系统HBN中,单元部件表示为网络根节点,在系统相互作用顺序图中,底层屏蔽区域表示为底层区域节点.为满足HBN概率推理的计算要求,两者的对应关系应选择条件概率分布来描述,即在EMS作用下单元部件的条件失效概率.此时,以相互作用顺序图的底层区域节点作为系统HBN新的根节点,对系统HBN进行了重构,从而建立系统电磁脉冲易损性评估模型,底层区域节点内EMS概率分布将作为评估模型概率推理的起点(输入量).

若系统外部电磁脉冲环境具有随机性,其幅度、极化方向和入射角度等参数都不确定,则根据EMT理论,计算得到外部电磁脉冲传导至系统底层屏蔽区域的EMS为随机量.沿用V(L,m)表示系统底层屏蔽区域内EMS的随机变量,则EMS概率分布表示为Pr(V(L,m)),m=1,2,…,ML.则系统HBN根节点X(L,m)(单元部件节点)及其非空父节点的联合概率可表示为

Pr(X(L,m),Pa(X(L,m))，VCL,m)

=Pr(X(L,m)|Pa(X(L,m)),V(L,m))

·Pr(Pa(X(L,m)))·Pr(V(L,m))

(3)

基于式(3),根节点X(L,m)的边际概率为

(4)

EMS概率分布Pr(V(L,m))理论上可通过EMT计算及实验测量获取.对于系统节点功能状态为成败型的情况,即X(l,m)={k},k=0,1,m=1,2,…,Ml,对应节点“正常”和“失效”两状态,如果已知区域层屏蔽区域V(L,m)内单元部件X(L,m)的失效分布为f(L,m)(e|θ),则阈值E(L,m)可通过(5)式确定

(5)

对于给定的置信度γ(L,m)可以计算出相应的阈值E(L,m),对不同的部件,γ(L,m)也可以采用不同的取值,γ(L,m)的取值实际反映了系统分析过程中对各单元部件易损性重要程度的认识.在实验研究中,γ=0.5是较常使用的取值方式,但从防护的角度,对于系统关键部件,可以采用较小的γ,比如γ=0.05.

确定阈值后,Pr(V(L,m))可以表示为

(6)

单元部件在电磁脉冲作用下的条件失效概率Pr(X(L,m)|Pa(X(L,m)),V(L,m))需通过电磁脉冲效应实验获取(实验室脉冲电流注入).

电子系统核电磁脉冲易损性评估模型建立过程可以归纳为以下步骤：

(1) 确定电子系统的外部电磁脉冲环境.

(2) 耦合分析.对电子系统的耦合通道进行分析,建立电磁脉冲与电子系统的相互作用顺序图.通过实验测量或理论计算,确定系统内各子系统、单元部件受到电磁脉冲作用的电流或电压激励(EMS).

(3) 可靠性分析.对受到EMS作用的子系统、单元部件进行功能分析,建立其对应的HBN.确定这些子系统、单元部件之间的功能逻辑关系.

(4) 建立系统电磁脉冲易损性评估模型.建立相互作用顺序图中底层屏蔽区域节点与该区域内HBN根节点的对应关系,建立同时具有耦合分析及可靠性分析能力的系统电磁脉冲易损性评估模型.

(5) 估计系统失效概率.确定底层屏蔽区域内EMS概率分布及单元部件在电磁脉冲作用下的条件失效概率,融合各子系统、单元部件的先验信息及效应试验数据,根据评估模型估计系统失效概率及置信度.

4 算例分析

4.1 建立系统电磁脉冲易损性评估模型

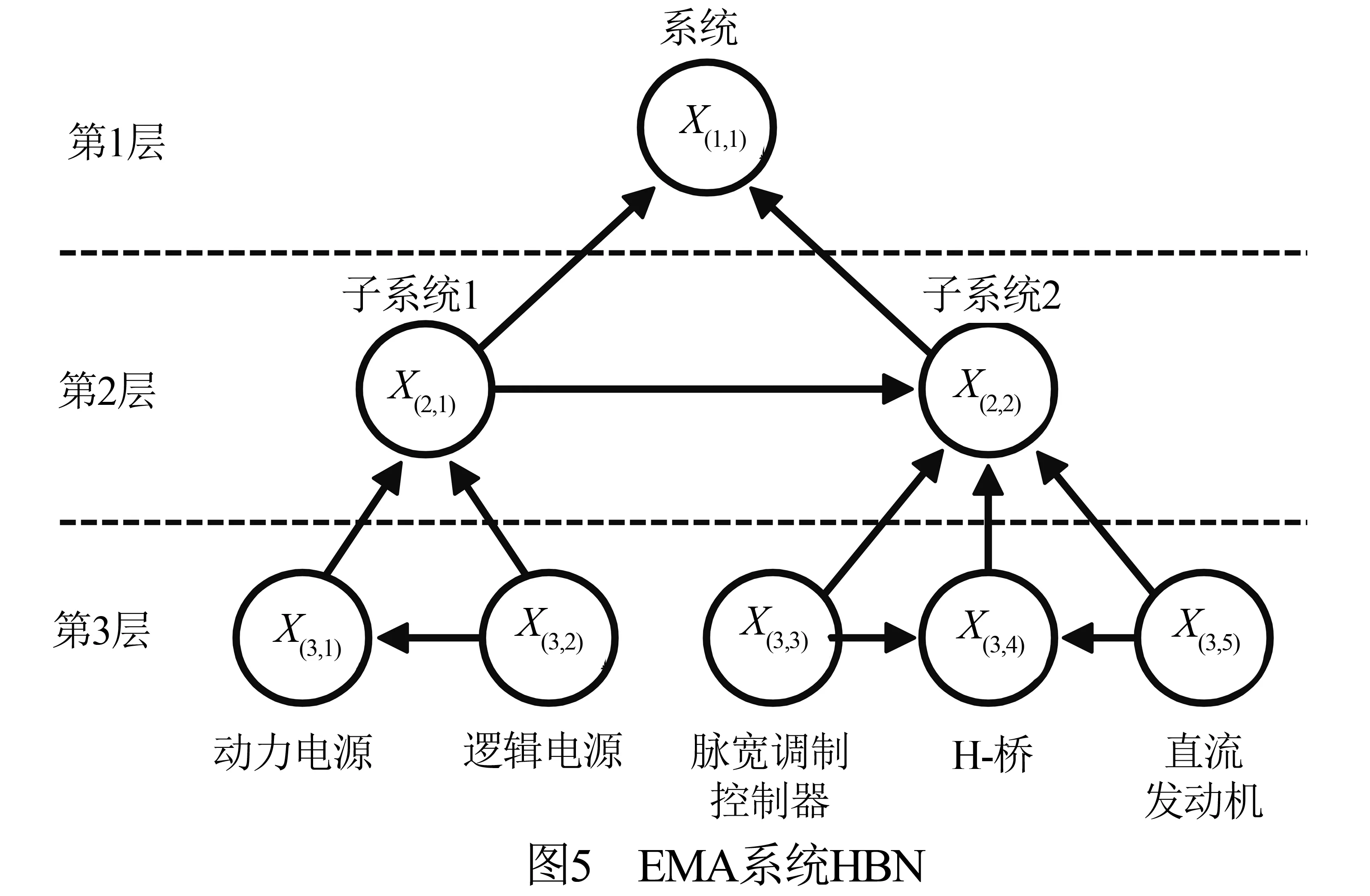
以某电子机械传动系统(Electro-Mechanical Actuator system,EMA)[17]为例,说明建模方法及计算过程.EMA系统可靠性框图如图4所示,系统HBN模型如图5所示.

假设系统、子系统及单元部件都满足GSA假设,根据EMT理论,系统拓扑图如图6所示,对应的系统电磁脉冲相互作用顺序图如图7所示.

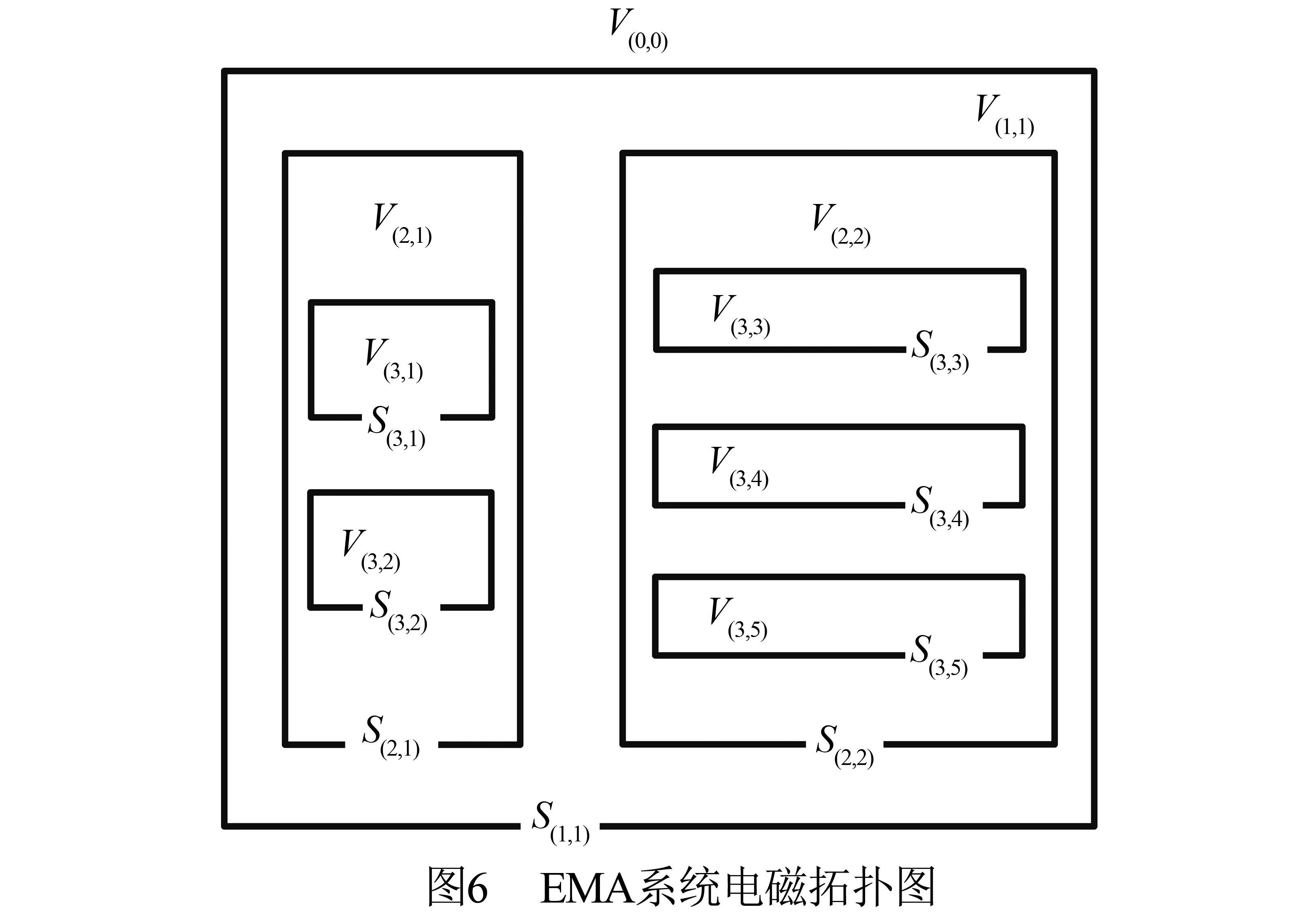
依据上述分析,系统底层屏蔽区域包含对应的系统单元部件,系统单元部件与子系统、系统之间的功能逻辑又构成了系统的HBN,则可以建立系统相互作用顺序图和HBN之间的拓扑连接,这种包含关系如图8所示.

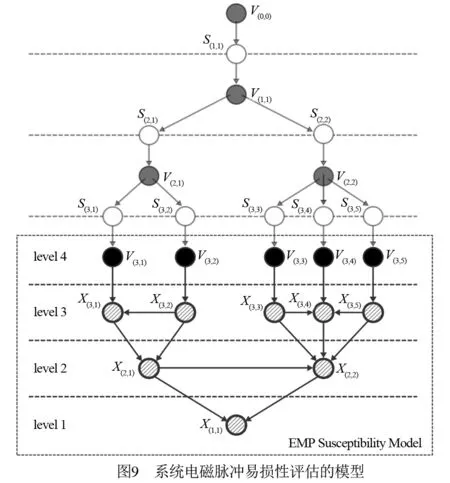
通过条件概率分布描述系统底层屏蔽区域与系统单元部件的拓扑连接,从而对系统HBN模型进行扩展,构建了EMT与HBN相结合的系统电磁脉冲易损性评估模型,如图9所示.

根据BN理论,系统可靠性通过节点X(1,1)的失效概率Pr(X(1,1))表示,有

Pr(X(1,1))=

·Pr(X(2,1))

(7)

根据图9的系统易损性评估模型,失效概率可进一步分解为

Pr(X(2,1))=

·Pr(X(3,2))

(8)

Pr(X(2,2)|X(2,1))=

·Pr(X(3,4)|X(3,3),X(3,5))·Pr(X(3,3))

·Pr(X(3,5))

(9)

Pr(X(3,1)|X(3,2))=

(10)

(11)

Pr(X(3,4)|X(3,3),X(3,5))

(12)

(13)

(14)

4.2 系统电磁脉冲易损性评估

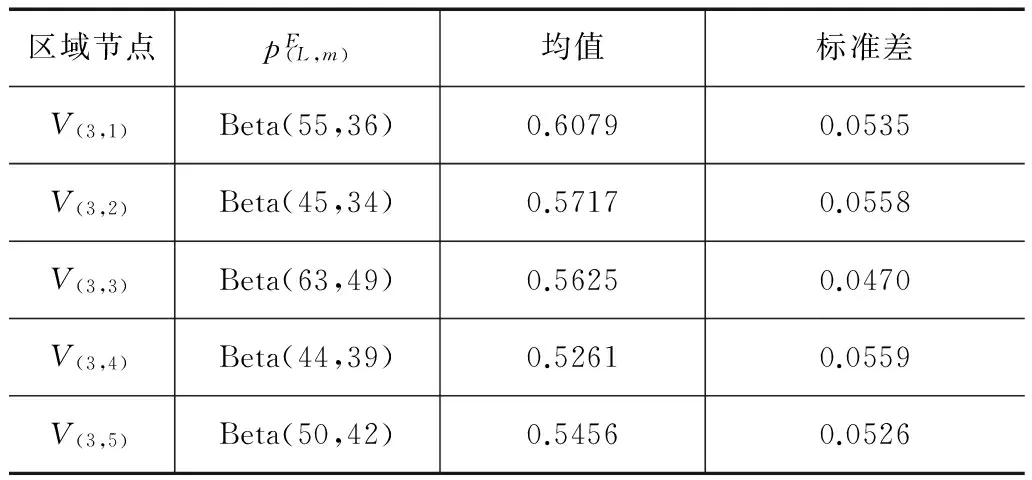
表1 底层屏蔽区域节点内电磁应力先验分布

由于只考虑了二态情况,根节点受电磁脉冲作用的条件失效概率可由单元部件电磁脉冲效应实验获得,一般采用脉冲电流注入法,其它CPTs则有专家给定,如表2所示.

表2 系统单元部件节点的条件概率表

系统虽然受到电磁脉冲作用产生效应,系统各节点功能状态发生改变,但系统内节点之间的功能逻辑关系不受影响,系统其它节点之间的CPTs如表3所示.

表3 系统及子系统的条件概率表

然后,将抽样得到的样本并代入HBN模型,可以计算得到系统内各节点的正常状态的概率结果.可应用最大熵方法对计算结果概率分布进行估计[24],或选定Beta分布,通过似然估计给出节点概率分布的参数.本文选定Beta分布参数似然估计方法,计算得到子系统及系统节点功能状态的概率密度函数,如图11所示,其中p0,(i,j)表示节点“正常”的概率密度函数,而p1,(i,j)为节点的失效概率密度函数,i,j=1,2.同时,对于相同参数条件设置,在未考虑同层节点级联失效关系时,又给出了HBN及FTA模型的计算结果作为对比,其中系统的FTA底事件概率即单元部件的失效概率,是通过单元部件受电磁脉冲作用的条件失效概率及底层屏蔽区域内电磁应力先验分布计算得到的,从而保证了BN与FTA输入参数相同,具备可比性.

从图中可以看出,①未考虑级联失效关系时,基于HBN和FTA计算得到的系统电磁脉冲易损性计算结果一致,说明了文中建模方法的有效性；②而考虑节点之间的级联失效关系时,基于HBN计算得到子系统及系统节点正常概率有所减小,反映了节点之间级联失效对系统电磁脉冲易损性的影响.

基于文中方法,各节点正常概率的主要统计量如表4所示.

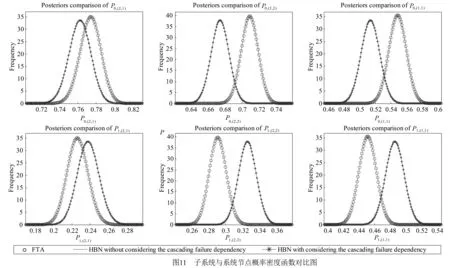
表4 系统内各节点正常概率计算结果统计

节点正常概率均值95%置信区间标准差Pr(X(3,1)=0)0.8731[0.8573,0.8882]0.0079Pr(X(3,2)=0)0.8723[0.8524,0.8911]0.0100Pr(X(3,3)=0)0.9052[0.8891,0.9202]0.0080Pr(X(3,4)=0)0.8653[0.8579,0.8726]0.0040Pr(X(3,5)=0)0.8882[0.8684,0.9066]0.0091Pr(X(2,1)=0)0.7617[0.7388,0.7839]0.0117Pr(X(2,2)=0)0.6742[0.6531,0.6949]0.0105Pr(X(1,1)=0)0.5135[0.4904,0.5366]0.0116

5 结论

本文研究了EMT理论中的ISD与系统HBN的拓扑关联关系,建立了电子系统电磁脉冲易损性评估的HBN模型.基于系统ISD,可以实现对系统电磁耦合通道的分析并确定系统底层屏蔽区域节点,通过定义底层屏蔽区域节点与系统单元部件节点之间的条件概率分布,融合系统可靠性信息与系统单元部件电磁脉冲易损性信息,从而建立系统电磁脉冲易损性评估模型.评估模型能够反映系统与电磁脉冲的相互作用过程,并对系统损伤情况进行较为准确的计算.另外,系统同层节点的失效具有普遍的相关特征,HBN能够有效地描述同级节点间的失效关系,较故障树分析等传统方法有所改进.而且,基于MC方法对HBN进行推理计算,可以获得系统节点易损性的不确定性计算结果.

文中建立的评估模型,目前仅考虑了底层屏蔽区域与单元部件的对应关系,若能进一步考虑子系统、系统节点与子系统、系统屏蔽区域的对应关系,则可对评估模型加以改善.在评估模型的基础上也可尝试系统故障分析及敏感性分析研究.

[1]Simon H A.The Sciences of the Artificial[M].Cambridge:The MIT Press,1996.

[2]乔登江.高功率电磁脉冲、强电磁效应、电磁兼容、电磁易损性及评估概论[J].现代应用物理,2013,4(03):219-224.

QIAO Deng-jiang.Introduction to HPEMP,IEME,EMC,and EM susceptibility and its assessments[J].Modern Applied Physics,2013,4(03):219-224.(in Chinese)

[3]王建国,牛胜利,张殿辉,等.高空核爆炸效应参数手册[M].北京:原子能出版社,2010.

Wang Jianguo,Niu Shengli,Zhang Dianhui,et al.The Parameter Manual Book of High-Altitude Nuclear Explosion Effects[M].Beijing:Atomic Energy Press,2010.(in Chinese)

[4]孟凡宝.高功率超宽带电磁脉冲技术[M].北京:国防工业出版社,2011.

Meng Fanbao.High Power EM Pulse Technology[M].Beijing:National Defense Industry Press,2011.(in Chinese)

[5]Kalab B.Analysis of Failure of Electronic Circuits from EMP-Induced Signals[R].AD778754,1973.

[6]王建国,刘国治,周金山.微波孔缝线性耦合函数研究[J].强激光与粒子束,2003,15(11):1093-1099.

Wang Jianguo,Liu Guozhi,Zhou Jinshan.Investigations on function for linear coupling of microwaves into slots[J].High Power Laser & Particle Beams,2003,15(11):1093-1099.(in Chinese)

[7]陶灵姣,吕承立,柴炎杰,等.地基C4I系统的高空核爆电磁脉冲易损性分析[J].火力与指挥控制,2010,35 (8):80-83.

Tao Lingjiao,Lv Chengli,Chai Yanjie,et al.Vulnerability modeling and assessment of maneuverable C4I system under the high power electromagnetic circumstance condition[J].Fire Control & Command Control,2010,35(8):80-83.(in Chinese)

[8]李勇,宣春,谢海燕,等.电磁脉冲作用下PIN二极管的响应[J].强激光与粒子束,2013,25(8):2061-2066.

Li Yong,Xuan Chun,Xie Haiyan,et al.Respone of PIN diode to electromagnetic pulse[J].High Power Laser and Particle Beams,2013,25(8):2061-2066.(in Chinese)

[9]Bevensee R M,Cabayan H S,Deadrick F J,et al.Probabilistic approach to EMP assessment[R].Livermore,CA:Lawrence Livermore National Laboratories (LLNL),UCRL-52804,1979.

[10]Mensing R W.Application of PRA to HEMP vulnerability analysis[R].Livermore,CA:Lawrence Livermore National Laboratories (LLNL),UCID-20553,1985.

[11]Mensing R W.A method for estimating the susceptibility of electronic system to HPM[R].Livermore,CA:Lawrence Livermore National Laboratories (LLNL),UCID-21430,1988.

[12]Bobbio A,Portinale L,Minichino M,Ciancamerla E.Improving the analysis of dependable systems by mapping fault trees into bayesian networks[J].Reliability Engineering and System Safety,2001,71:249-260.

[13]Pearl J F.Propagation and structuring in belief networks[J].Artificial Intelligence,1986,29(3):241:288.

[14]Boudali H,Duga J B.A continuous-time Bayesian network reliability modeling and analysis framework[J].IEEE Trans.Reliability,2006,55(1):86-97.

[15]周忠宝,周经伦,金光,等.基于贝叶斯网络的概率安全评估方法研究[J].系统工程学报,2006,21(6):636-643.

ZHOU Zhongbao,ZHOU Jinglun,JIN Guang,et al.Probabilistic safety assessment research based on Bayesian networks[J].Journal of Systems Engineering,2006,21(6):636-643.(in Chinese)

[16]霍利民,朱永利,范高锋,等.一种基于贝叶斯网络的电力系统可靠性评估新方法[J].电力系统自动化,2003,27(5):36-40.

Huo Limin,Zhu Yongli,Fan Gaofeng,et al.A new method for reliability assessment of power system based on Bayesian networks[J].Automation of Electric Power Systems,2003,27(5):36-40.(in Chinese)

[17]Li Mingyang,Liu Jian,Li Jing,et al.Bayesian modeling of multi-state hierarchical systems with multi-level information aggregation[J].Reliability Engineering and System Safety,2014,124:158-164.

[18]Heckerman D.A tutorial on learning with Bayesian networks[R].Washington:Microsoft Research,1996.

[19]Baum C E,Tom T K,Tesche F M.On the analysis of general multiconductor transmission-line networks[R].Interaction Notes,Albuquerque,NM:Air Force Research Lab.(AFRL),Note 350,1978.

[20]Baum C E.Electromagnetic Topology:A formal approach to the analysis and design of complex electronic systems[R].Interaction Notes,Albuquerque,NM:Air Force Research Lab.(AFRL),Note 400,1980.

[21]Tesche F M.On the addition of EM field propagation and coupling effects in the BLT equation[R].Interaction Notes,Albuquerque,NM:Air Force Research Lab.(AFRL),Note 588,2004.

[22]Parmantier J P,Alliot J C,Labaune G,et al.Electromagnetic coupling on complex systems:topological approach[R].Interaction Notes,Albuquerque,NM:Air Force Research Lab.(AFRL),Note 488,1990.

[23]Tesche F M.Topological concepts for internal EMP interaction[J].IEEE Trans Antennas Propag,1978,26(1):60-64.

[24]刘钰,韩峰,王玉恒,等.一种基于密度核估计的最大熵方法[J].工程数学学报,2011,28(3):285-292.

LIU Yu,HAN Feng,WANG Yu-heng,et al.A new maximum entropy method based on kernel density estimate[J].Chinese Journal of Engineering Mathematics,2011,28(3):285-292.(in Chinese)

刘 钰 男,1982年11月出生于陕西西安.西北核技术研究所博士研究生,西北核技术研究所助理研究员,研究方向为系统可靠性、系统辐射效应评估.

E-mail:liuyu05@nint.ac.cn

韩 峰 男,1975年8月出生于河南南阳.西北核技术研究所副研究员.研究方向为系统辐射效应评估,系统效能评估.

E-mail:hanfeng@nint.ac.cn

陆希成 男,1977年12月出生于江苏徐州.西北核技术研究所助理研究员.主要从事高功率电磁环境效应研究工作.

E-mail:luxicheng@nint.ac.cn

王建国 男,1965年12月出生于江苏.现为西北核技术研究所研究员,博士生导师,特聘为西安交通大学教授,博士生导师.主要从事瞬态电磁学,电磁场数值计算,天线设计和等离子物理等方面工作.

E-mail:wanguiuc@mail.xjtu.edu.cn

EMP Susceptibility Modeling and Assessment of Electronic System Based on Hierarchical Bayesian Networks

LIU Yu1,HAN Feng1,LU Xi-cheng1,WANG Jian-guo1,2

(1.DepartmentofNo.5,NorthwestInstituteofNuclearTechnology,Xi’an,Shaanxi710024,China;2.SchoolofElectronicandInformationEngineering,Xi’anJiaotongUniversity,Xi’an,Shaanxi710049,China)

A modeling method based on hierarchical Bayesian networks (HBN) which can be used in the susceptibility assessment of electronic system interfered by electromagnetic pulse (EMP) is proposed.According to the hierarchical structure of the electronic system and the feature of its EMP effects,steps to assess the system susceptibility are discussed.Analyzing the couple path by using the interaction sequence diagram (ISD),and the proper volume nodes of the base level of the ISD and the probability distribution of the electromagnetic stress in these nodes are determined.The topology relationship between the HBN and ISD is created by adding the directed arc from the base proper volume nodes of the ISD to the root nodes of HBN.The base proper volume level is considered as new root level to rebuild the HBN of system which can be used as the susceptibility assessment model of electronic system interfered by EMP.A case study demonstrates the effectiveness of the proposed methodology.

electromagnetic pulse(EMP); susceptibility; vulnerability; reliability; electronic system; hierarchical Bayesian networks; assessment model

2016-03-15;

2015-06-05 ；责任编辑：马兰英

国家自然科学重点基金(No.61231003); 国家自然科学基金青年基金(No.61201090)

TN07;N945.17

A

0372-2112 (2016)11-2695-09

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.11.019