一种基于规则的软件体系结构层性能演化优化方法
倪友聪,叶 鹏,杜 欣,陈 明,肖如良
(1.福建师范大学软件学院,福建福州 350117;2.伦敦大学学院计算机科学学院,英国伦敦 WC1E 6BT; 3.武汉纺织大学数学与计算机学院,湖北武汉 430200;4.湖南师范大学数学与计算机科学学院,湖南长沙,410081)
一种基于规则的软件体系结构层性能演化优化方法
倪友聪1,2,叶 鹏3,杜 欣1,陈 明4,肖如良1
(1.福建师范大学软件学院,福建福州 350117;2.伦敦大学学院计算机科学学院,英国伦敦 WC1E 6BT; 3.武汉纺织大学数学与计算机学院,湖北武汉 430200;4.湖南师范大学数学与计算机科学学院,湖南长沙,410081)
目前基于规则的软件体系结构(Software Architecture,简记为SA)层性能优化方法大多未充分考虑优化过程中规则的使用次数和使用顺序的不确定性,导致了搜索空间受限而难以获取更优的性能改进方案.针对这一问题并以最小化系统响应时间为优化目标,文中首先定义一种基于规则的SA层性能优化模型RPOM,以将SA层性能优化抽象为求解最优规则序列的数学问题;然后设计一种支持SA层性能改进规则序列执行的框架RSEF;进一步提出一种采用约束检查、修复及统计学习机制的演化求解算法EA4PO;最后以Web应用为案例与已有方法进行实验对比.结果表明:(1)本文方法较已有方法可以获取更短的系统响应时间;(2)EA4PO所引入的统计学习机制可显著提高演化求解算法的收敛速度和解质量.
性能评估;性能优化;软件体系结构;基于搜索的软件工程
1 引言
软件的性能是衡量软件系统质量的一个重要属性,性能的优劣已经成为系统成败的关键因素.在SA设计阶段进行性能的评估和预测,可以尽早地发现资源使用率过高、响应时间过长和吞吐量过小等性能问题,并通过相应的设计改进来缓解或消除这些问题,进而可在软件生命周期的早期达到性能优化的目的.
经过多年的研究和实践,人们已提出了排队网QN、分层排队网LQN、随机Petri网、随机进程代数和马尔可夫链等性能模型及其分析工具[1,2],在此基础上已涌现出了一些SA层性能评估和预测方法[3,4].这些方法能够将SA变换成某种性能模型,经过进一步的解析和分析后,可获取SA中相关软件元素和硬件元素的各项性能指标,进而可以评估和预测最终软件系统的性能.在SA层性能评估和预测技术的基础上,如何对SA进行自动改进以获得满足性能需求的SA设计方案已成为一个受到高度关注的研究主题[5].然而随着软件系统的规模越来越大、复杂性越来越高,影响性能的因素也随之增多,使得基于SA的性能改进空间也在不断增大[6].此外,在性能改进过程中常常需要满足各种不同的设计约束和限制,又致使性能改进空间呈现高度的非连续形态.在庞大且离散的性能改进空间中,如何自动找出SA层最优的性能改进方案,一直是软件工程工业界和学术界亟待解决的难题之一.
为了解决这一问题,目前已涌现出基于元启发[7,8]和基于规则[9~12]两类SA层性能自动优化方法.基于元启发的方法将SA层性能优化抽象为参数优化问题,并通过元启发搜索技术[13~15]进行求解.在预定义的优化参数上,元启发方法能在较大空间中搜索最优性能改进方案.然而元启发方法往往只能对组件部署、硬件配置和组件选择等少数几种SA参数进行优化[8],且大多数元启发方法尚未充分考虑将SA层性能改进知识应用到优化过程中,以提高算法的收敛速度或增加优化结果的可解释性.而基于规则的SA层性能优化方法则能以规则形式显式、精确地描述性能反模式[16].利用这些规则并借助相应的执行引擎可对SA的结构、行为和部署视图中的多种参数进行自动优化.基于规则的方法能按照一定的策略在所有规则组合所确定的性能改进空间中,搜索最优改进方案.然而由于规则的使用次数和使用顺序的不确定,往往导致规则的组合空间较为庞大.例如:Cortellessa和Trubiani等人针对12种SA层性能反模式,给出了对应的12条性能改进规则[9].即使在不考虑规则可以重复使用的情况下,由这12条规则不同的排列组合所确定的性能改进空间也将包含多于1212(近9000万亿)个候选的改进方案.已有的基于规则的方法大多未充分考虑规则的使用次数和使用顺序的不确定性,从而导致搜索空间受限,难以获取更优的性能改进方案.
2 相关工作
2.1 SA层性能改进规则及其执行引擎
SA层性能改进规则由条件和动作两部分组成.规则的条件部分用于诊断存在的性能问题,而动作部分则给出相应的改进方案.Cortellessa和Trubiani等人[9,10]基于SA元模型和一阶谓词,并运用逻辑规则描述了一组性能反模式.Mcgregor等人[12]通过综合考虑SA的可修改性,定义了一组性能改进规则.Xu等人[11]基于LQN模型并运用Jess框架定义了一组不特定于SA建模语言的性能改进规则.这些规则给出了资源瓶颈和响应时间长等性能问题的诊断条件以及对应的改进动作.为了支持SA层性能改进规则的自动执行,相应的规则执行引擎[9,11,12]也已被研发.
2.2 基于规则的SA层性能优化算法
在SA层性能改进规则及其执行引擎的支持下,优化算法运用一定策略在规则组合所构成的改进空间中,搜索具有最短系统响应时间的SA.这些优化算法主要采用步进式[9,10,12]、按轮迭代的深度优先[11]两种搜索策略,如图1和图2所示.图中弧上标记的r1,r2,…,rn表示n条性能改进规则;圆形结点表示SA;有向弧表示应用弧上标记的规则,将弧尾结点的SA改进为弧头结点的SA;搜索过程从根结点对应的初始SA开始.
步进式搜索策略总是将n条规则r1至rn分别应用到当前搜索结点上,具有最短系统响应时间的SA被选作下一次搜索的当前结点.如此反复,直至没有任何规则可以改进系统响应时间.按轮迭代的深度优先搜索策略则将n条规则划分成配置改进和设计改进两类规则.其中规则r1,r2,…,rm为m条配置改进规则,而规则rm+1,rm+2,…,rn为余下的n-m条设计改进规则.搜索首先进行初始的配置改进,然后再按轮进行迭代改进.在每轮改进中,总是先进行设计改进,然后进行配置改进.


从以上两种策略的搜索过程可以看出两点:一是从根结点至最终结点的路径上使用的规则所构成序列可以视为求解出的性能改进方案;另一是这两种搜索策略都没有充分考虑规则的不同使用次数和不同使用顺序可能形成的各种组合情况,因而只能搜索相对较小的空间,更优的改进方案可能被排除.
3 基于规则的SA层性能优化模型RPOM
RPOM模型可描述优化过程中规则的使用次数、使用顺序与最优性能改进方案之间的数学关系.下面给出它的具体定义.
定义1 定义函数r(SA)为根据SA求解并返回系统的响应时间.
定义2 从1至n依次对n条SA层性能改进规则进行编号,定义变换函数t(i,SA)表示将i(1≤i≤n)号规则应用到软件体系结构SA上,返回i号规则执行后的软件体系结构.
定义3 定义函数imp(i,SA)用于判定将i号规则应用到软件体系结构SA后,是否有性能改进效果.imp函数的定义如式(1)所示.

(1)
定义4 定义规则号序列X=
(2)
1≤xk≤n,(1≤k≤l)
(3)
hi(X)≤ui,(1≤i≤n)
(4)
定义5 在SA层性能改进方案X中,xk号规则的执行前软件体系结构BSA由式(5)定义.
(5)
(6)
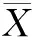
(7)

=0∧1≤k≤l)
(8)
4 SA层性能改进规则序列的执行框架RSEF
基于已有规则执行引擎,下面给出RSEF框架的总体结构和执行过程.
4.1 RSEF框架的总体结构


表1 T-RuleUseInSeq表的设计

4.2 RSEF框架的执行过程
RSEF框架的执行过程可由表2定义的ARSE算法进行描述.

表2 ARSE算法
5 基于规则的SA层性能演化优化算法EA4PO
EA4PO算法流程与传统遗传算法的类似,下面仅给出其个体编码、适应度计算、交叉和自适应变异算子.5.1 个体编码
在满足RPOM中式(2)和式(4)定义的同时,尽可能减少规则的使用次数,我们引入了一条特殊的、编号为0的空规则.约定当0号规则应用到任何软件体系结构将不做任何修改,即式(9)恒成立.规则号0的最多可能出现次数由式(10)定义,它是所有非0规则号的最多可能出现次数之和.
t(0,SA)=SA
(9)
(10)
l′=u0
(11)
(12)
hi(X′)≤ui,(0≤i≤n)
(13)
5.2 适应度计算
EA4PO中个体适应度值可用式(14)定义的fitness函数计算.适应度值越小,表明个体越优.

(14)
为了收集各个规则使用的启发式信息,在函数fitness的计算过程中建立了规则使用历史表T-RuleUseInHis,其设计如表3所示.其中,loc、rulNum和preRulNum三个字段构成T-RuleUseInHis表的主码.

表3 规则使用历史表T-RuleUseInHis
5.3带约束检查和修复机制的交叉算子
EA4PO的交叉算子包括交叉、约束检查和修复三个计算步骤.交叉步骤与一般的单点交叉操作相同.约束检查步骤对产生的两个中间个体,从交叉位开始至最后一位依次检查每位上的规则号是否违反式(13)定义的最多出现次数的约束,并记录所有违反约束的位.修复步骤将这些位上的规则号全部设置为0.
5.4 带约束检查和修复机制的自适应变异算子
EA4PO的变异算子采用带约束检查和修复机制的自适应单点变异算子.其包括基于统计学习的条件变异、约束检查和修复三个计算步骤.后两个步骤类似于5.3节中定义的约束检查和修复步骤.基于统计学习的条件变异定义如下.
定义8 函数nxtRulNum(i,m)表示在T-RuleUseInHis表中按第i位置上为规则号m的条件进行查找,并返回第i+1位置上所有出现的规则号构成的集合.
定义9 函数avgImpRate(j,k,q)表示在T-RuleUseInHis表中按第j和j-1位置上规则号分别是k和q(当j=1时,q=-1)的条件进行查找,计算结果记录impNum和totNum两字段值的商,称为k号规则的平均改进率.

(15)
(16)
(17)
6 案例研究
在基于规则的SA层性能优化方法中,仅Xu方法[11]所定义的规则是面向LQN模型[17]而不特定于具体的SA建模语言.考虑到Xu方法具有较好的通用性,故将其作为本文的对比方法.为了实证我们方法的有效性,以文献[11]中的Web应用(WebApp)为案例将我们的EA4PO与Xu按轮迭代的深度优先搜索算法(简称DFS)进行实验对比,并进一步将不带统计学习机制的EA4PO-与EA4PO进行比较,以实证采用统计学习机制的自适应变异算子可以提高演化求解算法的收敛速度和解质量.
6.1 WebApp案例
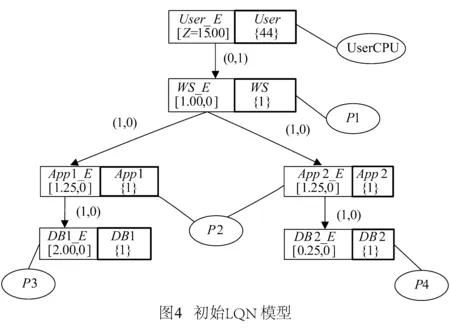
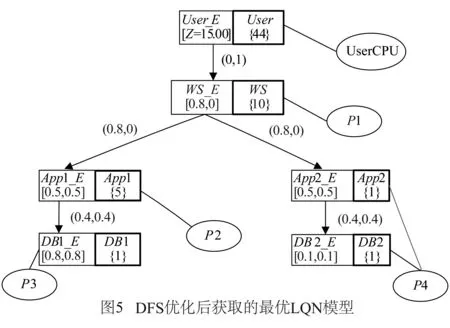
WebApp的初始LQN模型如图4所示,其对应的初始系统响应时间为179.71ms.文献[11]给出了WebApp案例所使用的6条性能改进规则r1至r6及其相关的参数值.Xu的DFS算法获取的WebApp优化后的LQN模型如图5所示,其对应的系统响应时间29.88ms,红色部分为优化后不同于优化前的模型参数值.DFS获取的性能改进方案是
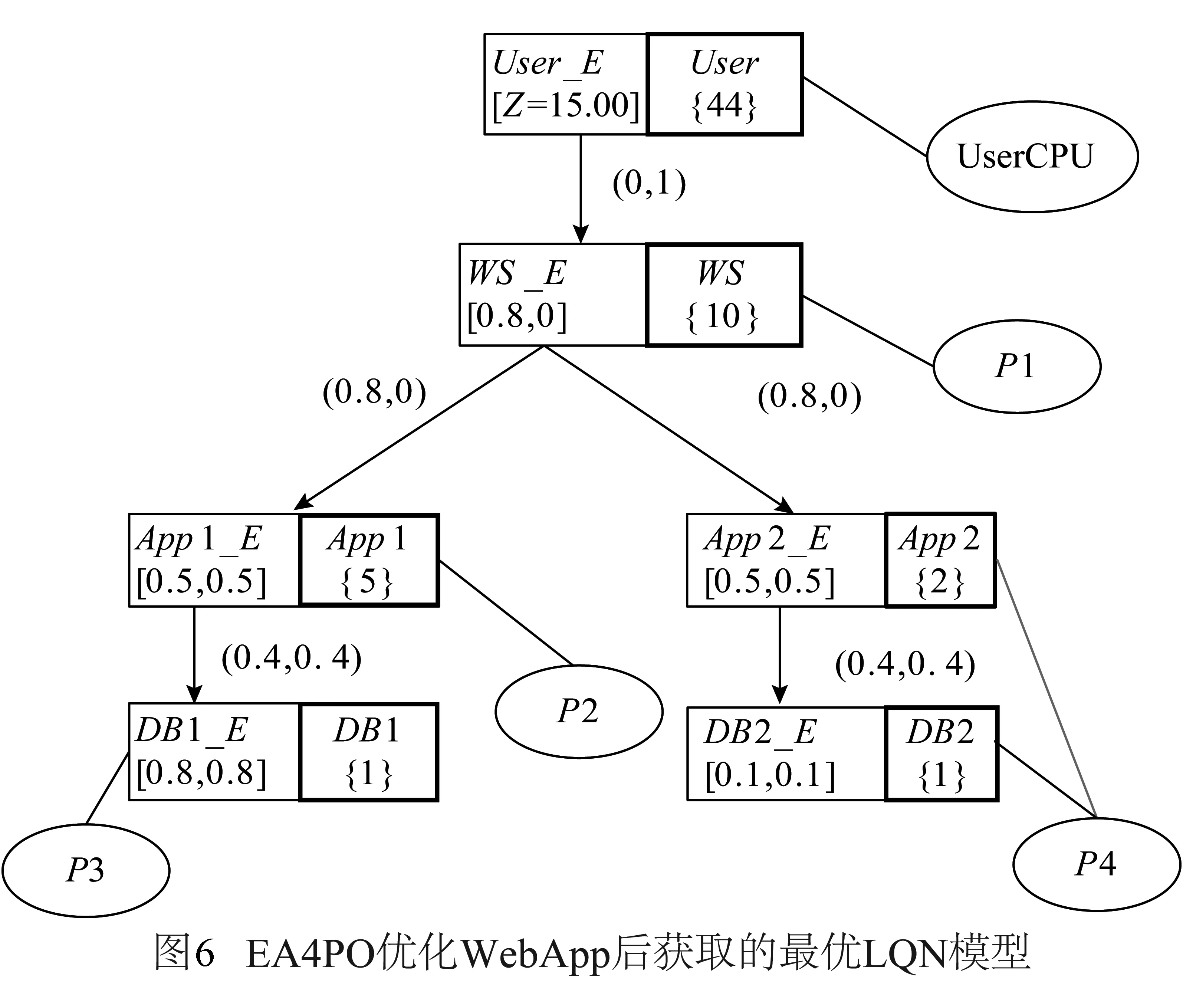
(1)EA4PO与Xu的算法比较 为了公平地比较,设置规则r1至r6相关的参数值与Xu方法相同.EA4PO中的种群大小、运行次数、演化代数、交叉概率和变异概率分别为15,20,30,0.6和0.3.EA4PO运行20次的结果如表4所示,其中第3、4、9、12、15、16、18、20次运行获取的结果响应时间是22.6ms,它们对应的LQN模型都是相同的,如图6所示.与图5中LQN模型的不同之处仅在于App2的多重性不同.从表4可看出,除了第10次运行的结果外,EA4PO获取的结果响应时间均优于DFS.我们使用Wilcoxon秩和检验对EA4PO和DFS获取的结果响应时间进行了统计检验.在置信水平α=0.05下,p-values=4.1696e-009<0.05,统计检验结果表明EA4PO显著优于DFS.

表4 EA4PO算法20次运行结果
此外,表4中第8行和第9行对应的改进方案都使用了规则r2,r3,r4和r5,且每个规则使用次数都相同,但这些规则的使用顺序不同导致了两次运行获得的结果响应时间明显不同.又如表4中第20行较第19行对应的序列仅在最后1位多出规则r2,其余部分全部相同.但就是仅多使用的这1次规则r2,却导致了获得的结果响应时间有着显著的不同.DFS因未充分考虑优化过程中各规则使用顺序和使用次数的问题而导致其搜索空间受限,难以获取更优的改进方案.
(2)EA4PO-与EA4PO比较 EA4PO-与EA4PO设置相同的种群大小、交叉概率和变异概率,分别为15,0.6和0.3.两个算法都独立运行20次,每次运行以连续20代结果响应时间不发生变化作为停机条件.采用文献[18]提出的收敛曲线图来表示所有20次运行中每隔两代最优解平均值的变化曲线.

从图7中可以看出EA4PO每次评估获取的平均结果系统响应时间均优于EA4PO-,其收敛曲线的下降速度要快于EA4PO-.使用Wilcoxon秩和检验对EA4PO和EA4PO-所获取的结果响应时间进行了统计检验.在置信水平α=0.05下,p-values=1.8803e-006<0.05,统计检验结果表明EA4PO显著优于EA4PO-.实验结果表明采用统计学习机制的自适应变异算子不仅可以加快算法的收敛速度,而且能够提高解质量.
7 结束语
文中提出了一种基于规则的SA层性能演化优化方法.首先定义了一种SA层性能优化模型RPOM,通过该模型精确刻画规则的使用次数、使用顺序与最优性能改进方案之间的关系,并将SA层性能优化抽象为求解最优规则序列问题;然后设计了一种用于支持SA层性能改进规则序列的执行框架RSEF,以支持RPOM的求解;进一步通过引入约束检查、修复及统计学习机制提出了一种高效的演化求解算法EA4PO,以搜索SA层最优性能改进方案.最后通过WebApp案例开展实验对比研究,实证了本文方法的有效性.下一步工作考虑将改进代价作为一个优化目标,研究基于规则的SA层性能多目标演化优化方法.
[1]Koziolek H.Performance evaluation of component-based software systems:A survey[J].Performance Evaluation,2010,67(8):634-658.
[2]Brosig F,et al.Quantitative evaluation of model-driven performance analysis and simulation of component-based architectures[J].IEEE Transactions on Software Engineering,2015,41(2):157-175.
[3]李传煌,等.一种 UML 软件架构性能预测方法及其自动化研究[J].软件学报,2013,24(7):1512-1528.
LI Chuan-Huang,et al.Performance prediction method for UML software architecture and its automation[J].Journal of Software,2013,24(7):1512-1528.(in Chinese)
[4]Cortellessa V,et al.Model-Based Software Performance Analysis[M].Berlin:Springer,2011.
[5]Aleti A,et al.Software architecture optimization methods:A systematic literature review[J].Software Engineering,IEEE Transactions on,2013,39(5):658-683.
[6]Koziolek A.Automated Improvement of Software Architecture Models for Performance and Other Quality Attributes[M].Karlsrule:KIT Scientific Publishing,2014.
[7]Martens A,Koziolek H.Automatic,model-based software performance improvement for component-based software designs[J].Electronic Notes in Theoretical Computer Science,2009,253(1):77-93.
[8]Etemaadi R,Chaudron M R.New degrees of freedom in metaheuristic optimization of component-based systems architecture:Architecture topology and load balancing[J].Science of Computer Programming,2015,97:366-380.
[9]Cortellessa V,et al.An approach for modeling and detecting software performance antipatterns based on first-order logics[J].Software & Systems Modeling,2014,13(1):391-432.
[10]Trubiani C,Koziolek A.Detection and solution of software performance antipatterns in palladio architectural models[J].Acm Sigsoft Software Engineering Notes,2011,36(5):19-30.
[11]Xu J.Rule-based automatic software performance diagnosis and improvement[J].Performance Evaluation,2012,69(11):525-550.
[12]Mcgregor J D,et al.Using arche in the classroom:One experience[R].Hanscom AFB,MA,USA:SEI,carnegie Mellon University,2007.
[13]Li Y,et al.An improved multiobjective estimation of distribution algorithm for environmental economic dispatch of hydrothermal power systems[J].Applied Soft Computing,2015,28:559-568.
[14]Li Y,et al.Dynamic-context cooperative quantum-behaved particle swarm optimization based on multilevel thresholding applied to medical image segmentation[J].Information Sciences,2015,294:408-422.
[15]Licheng J,et al.Quantum-inspired immune clonal algorithm for global optimization.[J].IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society,2008,38(5):1234-1253.
[16]Smith C U,Williams L G.Performance Solutions:A Practical Guide to Creating Responsive,Scalable Software[M].Redwood City,CA,USA:Addison-Wesley Longman Publishing Co.,Inc.,2002.
[17]Tribastone M.A fluid model for layered queueing networks[J].IEEE Transactions on Software Engineering,2013,39(6):744-756.
[18]Suganthan P N,Hansen N,et al.Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[R].Singapore:Nanyang Technological University,2005.

倪友聪 男,1976 年8月出生于安徽省肥西县.现为福建师范大学软件学院副教授、硕士生导师.主要研究领域为基于搜索的软件设计,软件体系结构等.
E-mail:youcongni@foxmail.com

叶 鹏 男,1976年12月出生于湖北省武汉市.现为武汉纺织大学数学与计算机学院讲师.主要研究领域为基于搜索的软件设计,软件体系结构等.
E-mail:whuyp@126.com

杜 欣(通信作者) 女,1979年2月出生于新疆河子市.现为福建师范大学软件学院副教授、硕士生导师.主要研究领域为基于搜索的软件工程,演化计算等.
E-mail:xindu79@126.com
An Approach for Rule-Based Performance Evolutionary Optimization at Software Architecture Level
NI You-cong1,2,YE Peng3,DU Xin1,CHEN Ming4,XIAO Ru-liang1
(1.FacultyofSoftware,FujianNormalUniversity,Fuzhou,Fujian350117,China; 2.DepartmentofComputerScience,UniversityCollegeLondon,London,WC1E6BT,UK; 3.CollegeofMathematicsandComputer,WuhanTextileUniversity,Wuhan,Hubei430200,China; 4.CollegeofMathematicsandComputerScience,HunanNormalUniversity,Changsha,Hunan410081,China)
In the existing rule-based performance optimization approaches at software architecture (SA) level,it has not been fully concerned that the count and the order of each rule usage are uncertain in the optimization process.As a result,the search space for performance improvement is limited and the better solutions are hard to find.Aiming to this problem and taking the system response time minimum as the optimization objective,firstly,a model called RPOM is defined to abstract rule-based software performance optimization at SA level as the mathematical problem for solving the optimal rule sequence.Secondly,a framework named RSEF is designed to support the execution of a rule sequence.Furthermore,an evolutionary algorithm named EA4PO is proposed to find the optimal performance improvement solution by introducing statistical learning,constraint checking and repairing.Finally,a web application is taken as a case in the experiments for comparing with the existing methods.The experimental results indicate that the shorter system response time can be obtained and the statistical learning can obviously improve the convergence rate and the solution quality in our approach.
performance evaluation;performance optimization;software architecture;search-based software engineering
2016-02-02;
2016-04-27;责任编辑:马兰英
国家自然科学基金(No.61305079,No.61370078,No.61402481); 武汉大学软件工程国家重点实验室开放基金(No.SKLSE 2014-10-02); 福建省自然科学基金(No.2015J01235); 福建省教育厅JK 类项目(No.JK2015006); 湖南省教育厅资助科研项目(No.14C0680); 河北省自然科学基金(No.F2015403046)
TP311
A
0372-2112 (2016)11-2688-07
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.11.018

