CMOS反相器低频噪声模型及可靠性表征研究

陈晓娟,陈东阳,吴 洁

(1.长春理工大学电子信息工程学院,吉林长春 130022;2.东北电力大学信息工程学院 吉林吉林 132012; 3.北华大学电气信息工程学院 吉林吉林 132013)



CMOS反相器低频噪声模型及可靠性表征研究

陈晓娟1,陈东阳2,吴 洁3

(1.长春理工大学电子信息工程学院,吉林长春 130022;2.东北电力大学信息工程学院 吉林吉林 132012; 3.北华大学电气信息工程学院 吉林吉林 132013)

为了表征CMOS反相器的可靠性,从其负载电流和输出电压的特性入手,详细推导了一种基于载流子波动理论的低频噪声模型,并由实验数据验证了模型的准确性.由实验结果可知,负载电流功率谱密度随频率的增加而减小,遵循1/f噪声的变化规律;得到了负载电流归一化噪声功率谱密度与器件尺寸的关系.通过深入研究1/f噪声与界面态陷阱密度的关系,验证了1/f噪声可用于表征CMOS反相器的可靠性,证明了噪声幅值越大,器件可靠性越差,失效率显著增大,为评价CMOS反相器的靠性提供了一种可行及有效的方法.

COMS反相器;低频噪声;可靠性;缺陷

1 引言

CMOS反相器是构成数字超大规模集成电路的基本单元,由P沟道和N沟道两个增强型MOS管串联组成,在电路中由它构成的逻辑非门或静态随机存取存储器具有静态功耗极低、抗干扰能力强、电源利用率高、输入阻抗大、带负载能力强等优点.目前在精密数字元件(如锁存器、数据选择器、译码器和状态机等)、整形、隔离、放大驱动、音频放大等领域等都有着广泛的应用.随着制程技术和CMOS技术按比例缩小的发展,CMOS混合集成技术和生产工艺日趋成熟,CMOS反相器在军用和民用领域都受到了普遍青睐.

CMOS反相器在工作状态下易受到器件参数变化、低频噪声和随机电报噪声等静态和动态波动的影响[1,2],这些大的波动会严重影响CMOS反相器的性能,降低其噪声容限[3],最终导致器件的可靠性下降.CMOS反相器中的杂质和缺陷(如氧化层陷阱、晶格错位、界面态等)会引起器件参数的变化,器件参数变化又会引起沟道载流子数波动或迁移率变化,使得其产生的低频噪声增加,且这些缺陷是影响CMOS反相器可靠性的重要因素[4],因此对CMOS反相器低频噪声的研究具有重要意义.

近年来,国内外学者对不同器件的低频噪声产生机理与其缺陷的关系[5]及可靠性表征做了大量研究,如VDMOS、光耦合器件、红外探测器、氮化镓基发光二极管、半导体激光器、电阻及DC/DC转换器等.本文根据噪声测试和数学推导,分析了CMOS反相器的噪声特性,建立了低频噪声物理模型,发现低频噪声可以有效地表征界面态陷阱密度,从而得到了低频噪声与CMOS反相器可靠性的关系.通过该研究能够对器件生产工艺改进、器件筛选和可靠性评估提供一种有效的方法.

2 CMOS反相器的低频噪声物理模型

CMOS反相器由两个增强型MOS管(nMOS和pMOS)组成,其中V1为nMOS驱动管,V2为pMOS负载管.nMOS和pMOS管的栅源开启电压分别为正值Vtn和负值Vtp,其数值范围在2～5V之间.为了使它能正常工作,要求电源电压Vdd大于二者的栅源开启电压绝对值之和,即Vdd>(Vtn+|Vtp|),其电路原理图如图1所示.

本文先从CMOS反相器的导电机制入手,讨论器件在不同工作区域时的载流子输运方式和器件沟道的状态,分析引起沟道载流子涨落的因素,建立低频噪声物理模型.由CMOS反相器的结构可知,流过的负载电流Idd可以通过pMOS漏电流Ip或者nMOS的漏电流In获得,其关系式如下,

Idd=Ip=In

(1)

利用相同的源极电压基准,每个沟道漏电流可以通过缓变沟道近似计算得出,其计算方法如下,

(2)

式中Vgs为栅源电压,Vds为漏源电压,Uc是随沟道变化的准费米能级,W是沟道的宽度,L是沟道的长度,μeff为载流子在有效电场下的有效电迁移率.由通用电子迁移规律[6,7]可知,Eeff有效电场强度是不能直接测量的参数,它与沟道反型电荷面密度Qi和区中耗尽电荷Qd有关,可表示为Eeff=(ηQi+Qd)/εsi(相对于电子η≈0.5,空穴η≈0.33),式中εsi为硅的介电常数,Qi可以利用朗伯W函数[8](Lambert W Function,LW)计算得到,其计算方法如下,

(3)

根据热电子发射模型,CMOS反相器载流子有效迁移率[9]可表示为,

μeff=μigexp(-φb/kT)

(4)式中μig为晶粒内部迁移率,φb为晶粒间界势垒高度.φb与晶粒间界陷阱态电荷和载流子浓度有关,其关系式如下,

(5)

式中Qgb为晶粒间界陷阱态电荷密度,n为沟道载流子浓度,εs为硅的相对介电常数.沟道载流子浓度n可表示为,

n=Qi/qtch

(6)

式中tch为反型层厚度,可由下式计算得出,

(7)式中tox为栅氧化层厚度,εox为硅氧相对介电常数,VG为栅极电压,VT沟道晶粒内部开始反型时对应的栅极电压.

在噪声分析中,我们最终关心的是平均噪声功率,参照确定的电压和电流信号使用的电路叠加原理,我们把两个噪声波形相加,并对得到的功率取平均值得,

(8)

式中Pav1、Pav2分别为x1(t)和x2(t)的平均功率.由于噪声为随机信号,因此噪声波形通常是非相关的,则式(8)可表示为,

Pav=Pav1+Pav2

(9)

从这个结果可以看出,噪声功率的叠加是成立的,同时也与噪声叠加原理相吻合.利用式(2)对漏电流微分[10],可得到,

(10)

由此可以看到式(10)中同时包含载流子电荷密度涨落δQi和有效迁移率涨落δμeff,二者同时作用会引起电流噪声.据此我们可以推出CMOS反相器中低频噪声功率谱的计算可以有以下两种方法:一种是从CMOS反相器的结构层面,把每个晶体管中考虑成独立的噪声源,然后用噪声功率的叠加原理将之叠加,经计算从而得到其功率谱密度;另一种是将反相器整体作为一个噪声源,估计整体它的整体噪声情况,然后计算其功率谱密度.

首先利用第一种方法对CMOS反相器进行分析,负载电流噪声功率谱密度SIdd可通过求和获得,即把每个晶体管漏电流噪声功率谱密度相加,其表达式如下,

SIdd=SIn+SIp

(11)

且可知,输出电压噪声功率谱密度SVout可通过nMOS和pMOS的漏电流功率谱密度除以相应的输出电导的平方得到,输出电导的求解方法如下,

gdn=δIn/δVout,gdp=δIp/δVout

(12)

则可求得SVout如下式,

(13)

应该注意的是,SVout不能通过负载电流噪声的功率谱密度除以整个反相器输出电导的平方来获得,因为当Idd为最大值时,gout(gout=δIdd/δVout)会被抵消掉,导致结果是非物理性的,不满足以上的推导.

利用第二种方法进行分析,对CMOS反相器低频噪声的整体计算,首先要明确每个晶体管中的低频噪声源.由于MOS晶体管中的低频噪声主要是由沟道介质面上的载流子的涨落引起的,在这种情况下,载流子数量的涨落的因素可以从平带电压波动或等效阈值电压变化的方面考虑[11].因此,负载电流噪声功率谱密度SIdd可由Idd波动作用的加和得到,这种波动是由于nMOS和pMOS晶体管中相互独立的阈值电压Vth的变化引起的,SIdd可由下式计算得出,

(14)

其中SVtn,p是nMOS和pMOS阈值电压功率谱密度,其计算方法如下,

(15)

式中Ntn,p是慢氧化界面态密度,λn,p是沟道衰减距离,f是频率.

同理,输出电压噪声功率谱密度可以直接由输出电压波动推到得到,式子如下,

(16)

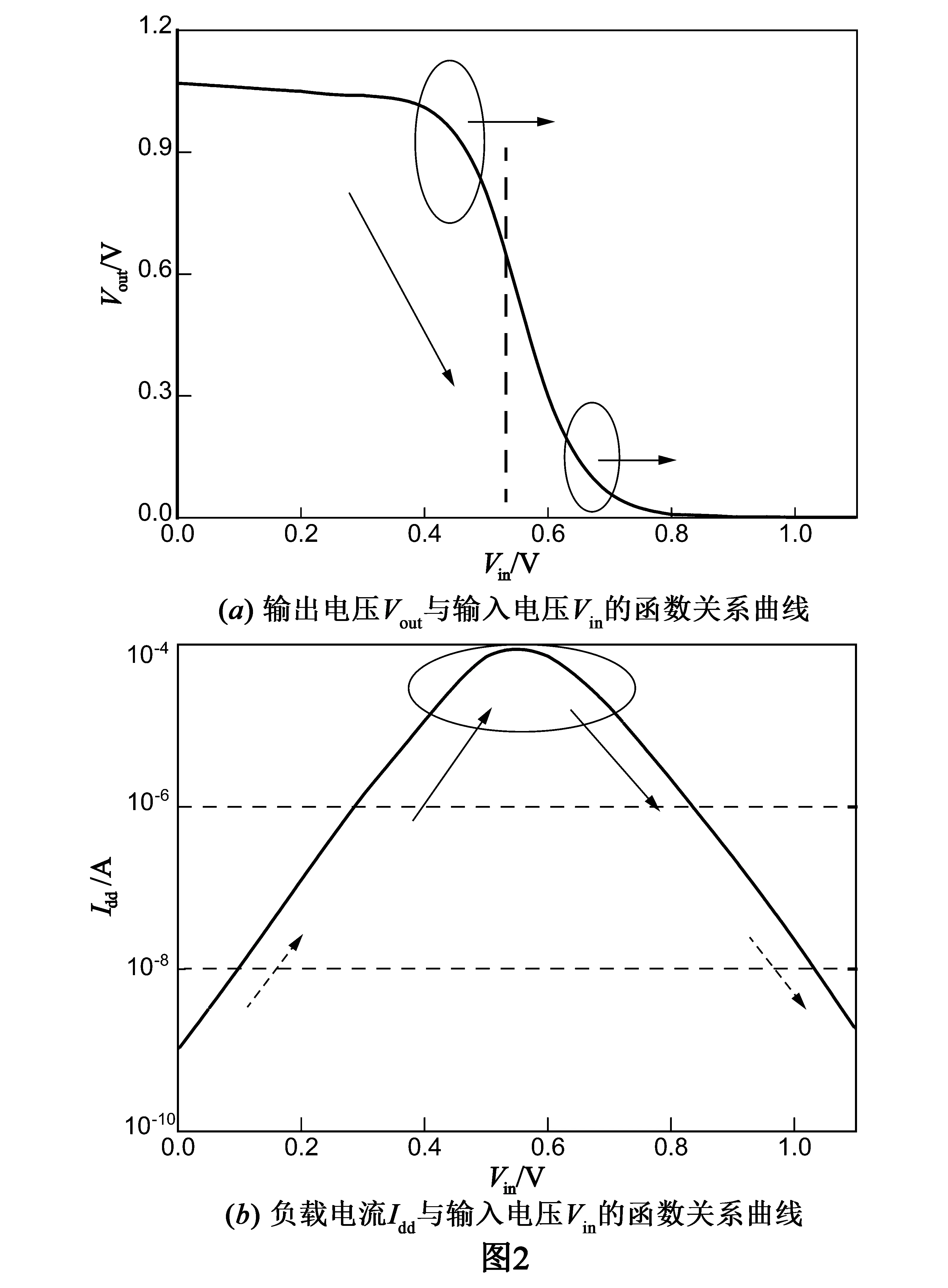
设定CMOS反相器的参数(Cox=1.8μF/cm2,n=1.7,Wn=3.24μm,,Ln=Lp=40nm,Vtn=Vtp=0.52V,μeff(Vgs=Vth)120cm2/Vs,DIBL=120mV/V),由反相器模型(1)～(7)可得到图2中的输出电压Vout、负载电流Idd与输入电压Vin之间的函数关系曲线.值得注意的是,当Vout=Vdd/2 时,Idd达到了最大值.

3 CMOS反相器低频噪声测量及模型验证

3.1 CMOS反相器低频噪声测量

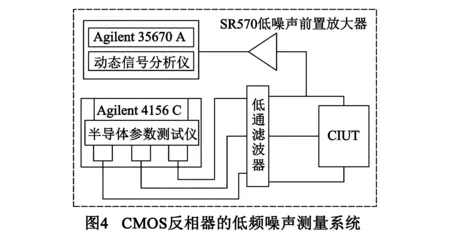
针对CMOS反相器的低频噪声测量系统如图4所示,系统采用精密半导体参数测试仪Agilent 4156C作为直流电压源通过低通滤波器给被测CMOS反相器(CMOS Inverter Under Test,CIUT)提供栅极偏压,采用SR570低噪声前置放大器对噪声信号放大,且通过其内部电源为被测CMOS反相器提供漏极偏压,反相器源极接地,最后采用Agilent 35670A动态信号分析仪对放大后的噪声信号进行快速傅里叶变换FFT,得到噪声功率谱密度[12,13].

3.2 噪声模型验证

基于所搭建的CMOS反相器低频噪声测量系统,对其进行测试与分析,以验证上述模型及研究其可靠性的噪声表征方法.在器件参数与前文一致的条件下,所测得的输出电压Vout、负载电流Idd与输入电压Vin的实验特性曲线如图5所示,由图5可知:实验结果与图2中的模型特性曲线表现基本一致,满足低频噪声模型式(1)～(7),当Vout=Vdd/2时,Idd达到了最大值.

基于上述的测量条件,在Vdd从3V开始增大的情况下,所测得器件负载电流Idd涨落的功率谱密度SIdd随Vdd变化如图7所示,随着器件Vdd的增加,负载电流随之增加,因而SIdd将随着Vdd增加而增加.

由图7可知,SIdd随频率的变化遵循1/f的变化规律,满足经典的1/f噪声理论,此时氧化层陷阱的表面势被电荷的波动所调制,这导致了沟内的载流子数目无规则变化,同时库仑散射也将被调制,并且引起沟的迁移率的升降,因此,导致沟道电流的变化;当频率高于8 kHz时,SIdd随频率的变化加剧,这是受产生-复合效应(g-r噪声)的影响.

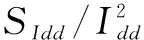
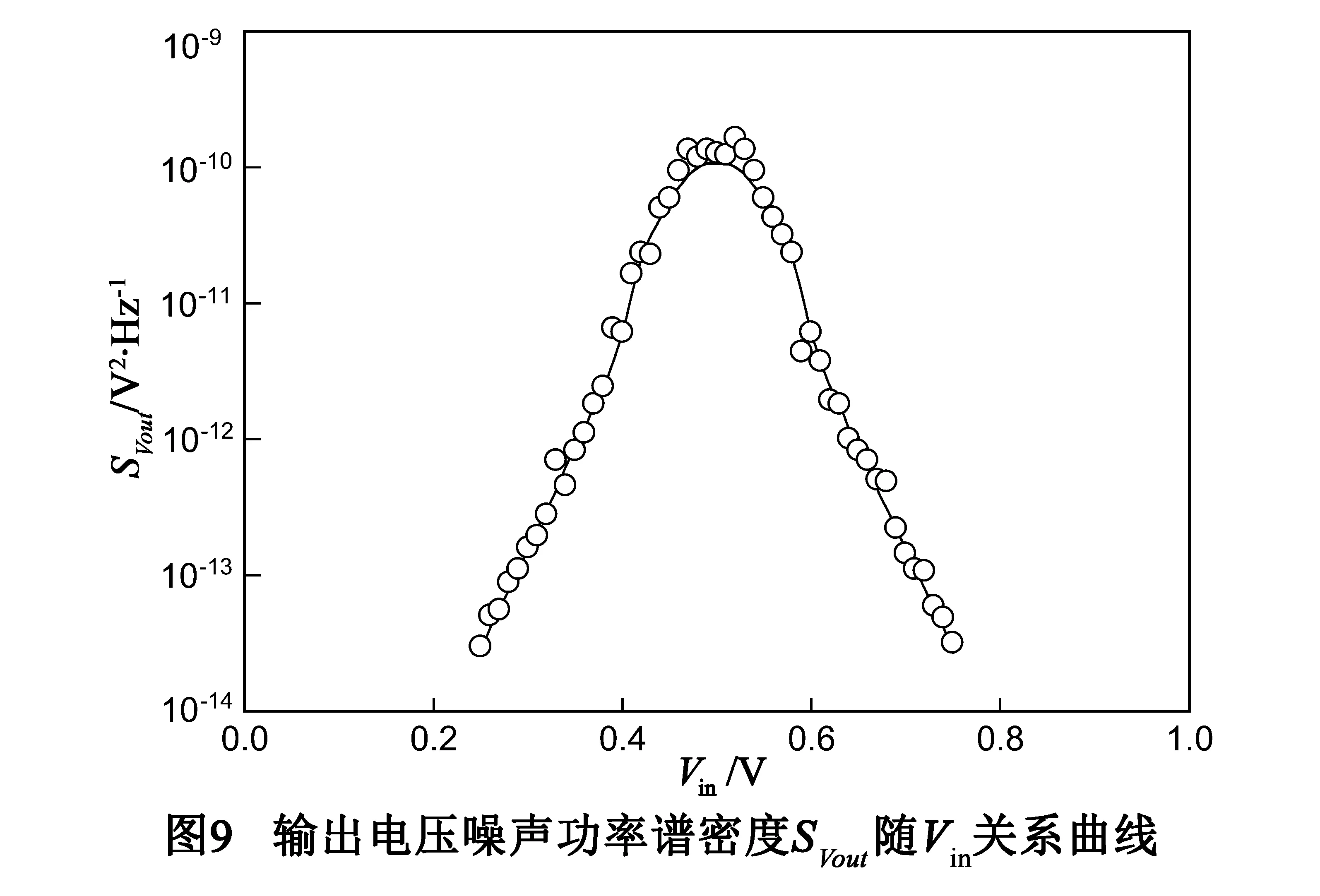
输出电压噪声功率谱密度SVout的测量结果如图9所示,从图中我们可以看到,实际测量得到的SVout与由模型(13)、(15)、(16)计算得到的输出电压噪声功率谱表现基本一致.图9表明SVout在Vdd一定的条件下,SVout随Vin钟形变化,并在Vin=0.5V时有最大值.

4 可靠性的噪声表征

表征CMOS反相器可靠性并对其可靠性评价的常规方法有:可靠性试验、加速寿命试验、高低温循环实验和抽样等.这样的方法试验周期较长,且一般是随机抽样对少数样品进行实验,结果是统计量,不确定性强,还可能对器件造成不可逆的损伤.所以,为了更好地表征和评价 CMOS反相器的可靠性,就迫切需要一种能快速、灵敏、无损的方法.通过对CMOS反相器老化试验的研究可知,器件老化后的界面态陷阱密度会成倍的增加.

CMOS反相器中的1/f噪声是由于两个MOS管的陷阱态空间、杂质浓度分布梯度、能量上的非均匀分布、费米能级在禁带中位置的连续变化、来自于外界或内部形成的过应力给器件带来的损伤及接触不良等原因产生的[15],研究表明,这都与器件表面或界面处的缺陷有关,这些缺陷将会影响材料中定态对自由载流子的俘获和发射,位于SiO2-Si界面过渡层和沟道内载流子的涨落与界面态陷阱密度(范围在109～1012eV-1·cm-2之间)强烈相关[16],且知1/f噪声是电子器件结构均匀性的一种灵敏的表征参数,因此1/f噪声可用于器件的表面缺陷与可靠性的表征.由以上建立的CMOS反相器低频噪声模型可得,负载电流噪声功率谱密度与表面缺陷能量密度的关系如下[17],

(17)

式中E为界面缺陷能级,PE为载流子占缺陷能级的概率,τ为时间常数,它分布较广,通常在几个至十几个数量级内变化.由于COMS反相器有源区的尺寸已可做到零点几个微米,所以只有能量在费米能级Uc附近几个kT范围内的陷阱才对低频噪声有贡献[18],因此可对式(17)化简为

(18)

式中A为CMOS反相器MOS管陷阱激活区体积.通过测量反相器的负载电流噪声功率谱密度与式(18)可得Nt和Vdd关系,如图10所示.

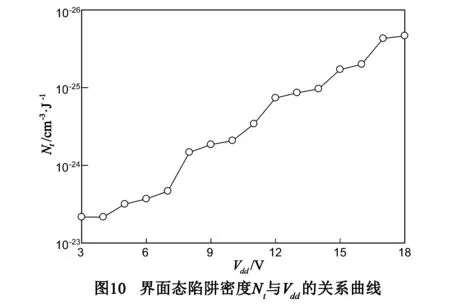
由图可知,界面态陷阱密度Nt随着Vdd的增大而增加,这与前文分析的1/f噪声与界面态陷阱密度Nt成正比关系相符合,同时这也与图7表现出的特性相一致.

由此可知,低频噪声可用于表征CMOS反相器的可靠性,如发现CMOS反相器的1/f噪声明显较大,则说明这样的器件越容易老化、失效.同时通过实验也可知,利用低频噪声对CMOS反相器进行可靠性分析的结果与传统方法得到的结果一致.

5 结论

本文根据CMOS反相器的低频噪声特性,从基本物理量和噪声叠加原理出发,建立了CMOS反相器的低频噪声模型,并通过实验证实了实验结论与理论推导结果的一致性.由实验结果可知,CMOS反相器的低频噪声随频率的变化遵循1/f的变化规律,满足经典的1/f噪声理论,本文对该结果进行了解释,并对其低频噪声特性进行了验证.提出了1/f噪声可用于表征CMOS反相器的表面缺陷与可靠性,研究了1/f噪声与界面态陷阱密度的关系,得到了不同下的界面陷阱态密度.由此可知,CMOS反相器的可靠性与其表现出的1/f噪声成反比关系,若其1/f噪声较小,则说明其可靠性较高;反之,若其1/f噪声明显较大,则说明这样的器件越容易老化、失效,可靠性低.

[1]Mezzomo C,Bajolet A,Cathignol A,DiFrenza R,Ghibaudo G.Characterization and modeling of transistor variability in advanced CMOS technologies[J].IEEE Trans Electron Dev,2011,58(8):2235-2248.

[2]庄奕琪,孙青.半导体器件中的噪声及其低噪声化技术[M].北京:国防工业出版社,1993:64-100.

Zhuang Y Q,Sun Q,Noise and Minimizing Technology in Semiconductor Devices[M].Beijing:National Defense Industry Press,1993:64-100.(in Chinese)

[3]Mahmutoglu A G,Demir A.Modeling and simulation of low-frequency noise in nano devices:stochastically correct and carefully crafted numerical techniques[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2015,34(5):794-807.

[4]黄杨程,刘大福,梁晋穗,龚海梅.短波碲镉汞光伏器件的低频噪声研究[J].物理学报,2005,54(05):2261-2266.

Huang Y C,Liu D F,Liang J S,Gong H M.Low frequency noise study on short wavelength HgCdTe photodiodes[J].Acta Phys.Sin.2005,54(05):2261-2266.(in Chinese)

[5]Ioannidis E G,Haendler S,Dimitriadis C A,Ghibaudo G.Characterization and modeling of low frequency noise in CMOS inverters[J].Solid-State Electronics,2013,81(3):151-156.

[6]Takagi S,Toriumi A,Iwase M,Tango H.On the universality of inversion layer mobility in Si MOSFET's:Part I-effects of substrate impurity concentration[J].IEEE Trans Electron Dev,1994,41(12):2357-2362.

[7]支天,杨海钢,蔡刚,秋小强,李天文,王新刚.嵌入式存储器空间单粒子效应失效率评估方法研究[J].电子与信息学报,2014,36(12):3035-3041.

Zhi T,Yang H G,Cai G,Qiu X Q,Li T W,Wang X G.Study on the prediction of single-event effects induced failure rate for embedded memories[J].Journal of Electronics & Information Technology,2014,36(12):3035-3041.(in Chinese)

[8]包军林,庄奕琪,杜磊,李伟华,万长兴,张萍.n/p沟道MOSFET1/f噪声的统一模型[J].物理学报,2005,54(05):2118-2122.

Bao J L,Zhuang Y Q,Du L,Li W H,Wan C X,Zhang P.A unified model for1/f noise in n-channel and p-channel MOSFETs[J].Acta Physica Sinica.2005,54(05):2118-2122.(in Chinese)

[9]陈文豪,杜磊,庄奕琪,包军林,何亮,陈华,孙鹏,王婷岚.电子器件散粒噪声测试方法研究[J].物理学报,2011,60(05):165-172.

Chen W H,Du L,Zhuang Y Q,Bao J L,He L,Chen H,Sun P,Wang T L.Shot noise measurement methods in electronic devices[J].Acta Physica Sinica.2011,60(05):165-172.(in Chinese)

[10]刘远,吴为敬,李斌,恩云飞,王磊,刘玉荣.非晶铟锌氧化物薄膜晶体管的低频噪声特性与分析[J].物理学报,2014,63(09):422-427.

Liu Y,Wu W J,Li B,En Y F,Wang L,Liu Y R.Analysis of low-frequency noise in the amorphous indium zinc oxide thin film transistors[J].Acta Physica Sinica.2014,63(09):422-427.(in Chinese)

[11]陈晓娟,陈东阳,申雅茹.基于低频噪声测量的UPS故障诊断方法[J].电子器件,2015,38(2):1-5.

Chen X J,Chen D Y,Shen Y R.UPS fault diagnosis method based on low frequency noise measurement[J].Chinese Journal of Electron Devices,2015,38(2):1-5.(in Chinese)

[12]Choi H S,Jeon S,Kim H,Shin J,Kim C,Chung U I.Verification of interface state properties of a-InGaZnO thin-film transistors with SiNxand SiO2gate dielectrics by low-frequency noise measurements[J].IEEE Electron Device Letters,2011,32(8):1083-1085.

[13]Ioannidis E G.,Haendler S,Manceau J P,Dimitriadis C A,Ghibaudo G.Impact of dynamic variability on the operation of CMOS inverter[J].Electronics Letters,2013,49(19):1214-1216.

[14]Chen X J,Chen D Y.Method of noise measurement for inverter fault diagnosis[J].ICIC Express Letters,2015,7(9):42-48.

[15]Jevtic M M.Noise as a diagnostic and prediction tool in reliability physics[J].Microelectronics Reliability,1995,35(3):455-477.1925.

[16]Barton D L,Osinski M K.Single-quantum well InGaN green light emitting diode degradation under high electrical stress[J].Microelectronics and Reliability,1999,39(8):1219-1227.

[17]Mohammadi S,Pavlidis D.A nonfundamental theory of low-frequency noise in semiconductor devices[J].IEEE Transactions on Electron Devices,2000,47(11):2009-2017.

[18]Lopez D,Haendler S,Leyris C,Bidal G,Ghibaudo G.Low-Frequency Noise Investigation and Noise Variability Analysis in High-k/Metal Gate 32-nm CMOS Transistors[J].IEEE Trans Electron Dev,2011,58(8):2310-2316.

陈晓娟 女,1970年出生,吉林长春人,长春理工大学电子信息工程学院教授、博士生导师,主要研究方向为模拟电路故障诊断以及电力线通信.

E-mail:cxj-neiep@126.com

陈东阳(通信作者) 男,1989年出生,黑龙江哈尔滨人,东北电力大学信息工程学院硕士研究生,主要研究方向为微弱信号检测、电子器件与模拟电路可靠性.

E-mail:c-dongyang@163.com

Investigation on Low-Frequency Noise Models and Representation for Reliability of CMOS Inverter

CHEN Xiao-juan1,CHEN Dong-yang2,WU Jie3

(1.SchoolofElectronicInformationEngineering,ChangchunUniversityofScienceandTechnology,Changchun,Jilin130022,China；2.SchoolofInformationEngineering,NortheastDianliUniversity,Jilin,Jilin132012,China；3.SchoolofElectricalInformationEngineering,BeihuaUniversity,Jilin,Jilin132013,China)

In order to characterize the reliability of CMOS inverter,a kind of low-frequency noise model is deduced in detail by using the characteristics of load current and output voltage,based on the carrier fluctuation theory,and the accuracy of the model was verified by experimental data.The experiment results indicate that load current power spectral follows the changing rule of the 1/fnoise,decreasing with the increase of frequency;the normalized noise power spectral density of load current decreases with the increase of the channel width or length.Using the experimental data,the relationship between 1/fnoise and interface trap state densityof CMOS inverter is established.Verify that the 1/fnoise can be used to characterize the reliability of CMOS inverter.It is proved that the larger interface trap state density,the larger the noise magnitude,leading to the degradation of device reliability and significant rise in device invalidation rate.That provides a feasible and effective method for evaluating the reliability of CMOS inverter.

CMOS inverter;low-frequency noise;reliability;defect

2015-03-30;

2015-11-17;责任编辑:马兰英

国家自然科学基金(No.61271115)

TN94

A

0372-2112 (2016)11-2646-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.11.012