具有几何不变性的图像复制-粘贴盲鉴别算法
吕颖达,申铉京,陈海鹏
(1.吉林大学计算机科学与技术学院,吉林长春 130012;2.吉林大学符号计算与知识工程教育部重点实验室,吉林长春 130012; 3.吉林大学公共计算机教学与研究中心,吉林长春 130012)
具有几何不变性的图像复制-粘贴盲鉴别算法
吕颖达1,2,3,申铉京1,2,陈海鹏1,2
(1.吉林大学计算机科学与技术学院,吉林长春 130012;2.吉林大学符号计算与知识工程教育部重点实验室,吉林长春 130012; 3.吉林大学公共计算机教学与研究中心,吉林长春 130012)
提出一种具有几何不变性的复制-粘贴盲鉴别算法.该算法首先定义灰度级别和灰度结构,根据像素的灰度级别划分图像块,再结合其灰度结构定位可疑块对;然后对每一组可疑块对进行基于对数极坐标变换的相位相关,并粗略定位篡改区域;最后,精确计算篡改区域之间的旋转角度、缩放尺度及平移量,从而定位复制-粘贴区域.实验结果表明,该算法不但具有旋转、缩放等几何不变性,而且具有较高检测效率及较强的鲁棒性.
盲鉴别;复制-粘贴篡改;对数极坐标变换;相位相关
1 引言
数字图像盲鉴别技术也称为数字图像内容取证技术(Digital image content forensics),通过分析图像的统计特性,对其原始性、真实性、完整性及反映场景的客观性进行检测与判断[1].作为保护图像内容安全的新思路,数字图像盲鉴别技术已经成为相关领域的研究热点[2~4].
图像区域的复制粘贴操作是最常用的篡改手段之一,通常是把图像中的某一个区域复制粘贴到另一个区域,以隐藏重要目标或者造成某种假象.目前,针对复制-粘贴篡改的盲检测主要分为两种方法:
(1)基于图像块匹配的盲鉴别方法
2003年,Fridrich通过匹配图像块的DCT(Discrete Cosine Transform)系数矩阵,定位复制-粘贴区域[5].为了提高算法对后处理操作的鲁棒性,Wang和Cao分别提出了改进的基于DCT系数的盲鉴别算法[6,7].另外,为了降低错误检测率,Hu将DCT系数进行了分类,但该算法仅对噪声有较好的鲁棒性[8].Popescu等人利用主成分分析(Principal Component Analysis,PCA)的方法,实现了复制-粘贴篡改区域的定位[9].然而以上算法均不能检测经过旋转、尺度变换等几何变换的复制-粘贴篡改.
于是,相关学者将不变矩应用到复制-粘贴检测中.Mahdian通过匹配图像块实现了复制-粘贴的盲鉴别[10].Ryu提出基于Zernike矩的复制-粘贴盲鉴别算法[11].该算法对噪声、模糊和JPEG重压缩具有较好的鲁棒性,但是对除旋转外的几何变换的检测效果较弱.2013年,Ryu改进了该算法,采用LSH (Locality Sensitive Hashing)降低了计算复杂度和误匹配率[12].Liu提出基于Hu不变矩的复制-粘贴盲鉴别算法[13].但是,该算法不能定位经过尺度变换的复制-粘贴篡改.Davarzani等人采用局部二值模式LBP (Local binary patterns)进行复制-粘贴盲鉴别,对旋转等几何变换和模糊、噪声、JPEG重压缩等后处理操作取得了较好的鲁棒性[14].Leida Li等人首先利用圆形重叠分块代替传统的矩形分块.然后针对每一个圆形块,采用极谐变换提取其具有旋转、缩放不变性的特征,并且进行特征匹配.最后,去除误匹配并利用形态学方法获得最终的检测结果,并且通过实验证明了该方法的仿射不变性[15].
(2)基于特征点匹配的盲鉴别方法
Huang 首先将特征描述子SIFT(Scale Invariant Feature Transform)应用于复制-粘贴盲鉴别中[16].Amerini改进了SIFT算法,对SIFT特征点进行分层聚类,淘汰特征点较少的类,以去除误匹配[17].为了提高算法效率,Xu等人提出了基于SURF特征的复制-粘贴盲检测算法[18].Guo提出了基于改进DAISY的复制-粘贴盲鉴别算法,对特征点较少的复制-粘贴区域具有较好的检测效果[19].2014年,Mohammad等人对小波变换后的低频图像,进行基于SIFT的复制粘贴检测,获得了更多匹配的特征点[20].Jian Li等人首先利用图像分割的方法对图像进行分块,然后对每一个块对进行关键点匹配并估计仿射变换的矩阵,最后利用极大似然估计法来确定可疑块对之间的仿射变换.实验结果表明,该算法的检测率具有明显优势[21].Ewerton等人结合多尺度分析和复制区域的投票分析,并利用SIFT特征点匹配,提出了复制粘贴盲鉴别算法,该算法能够抵抗旋转、缩放变换,具有较强的鲁棒性,并且有效去除了误匹配[22].
通过以上分析可知,目前复制-粘贴盲鉴别算法尚存在如下不足:(1)基于图像块匹配的盲鉴别算法对图像分块通常采用“滑窗”方法,如文献[5~14]的算法,但是通过多次实验分析发现,针对不同的鉴别目标,窗口大小的选择显著影响了检测效率和准确度,窗口过小会使分块增多而且特征不明显,窗口过大会导致检测块大于实际篡改块的大小而使算法直接失效.另外,采用图像块匹配进行复制-粘贴盲鉴别时,针对旋转、缩放等几何变换,大多比较脆弱,如文献[10~13]算法,而且文献[5~9]算法无法检测经过几何变换的复制-粘贴区域.(2)基于特征点匹配的盲鉴别算法的计算复杂度依赖于检测到的特征点数量,因此其计算复杂度一般较高[16].另外,针对平滑的背景区域,检测到的特征点会比较少.因此,对于复制背景来遮盖目标的隐藏目标类的复制-粘贴篡改,该类鉴别算法的检测效果不理想.
基于此,本文以图像块匹配为切入点,提出具有几何不变性的复制-粘贴盲鉴别算法.该算法定义图像的灰度级别和灰度结构,根据该特征对图像进行分块并定位可疑块对,从而避免分块不确定的问题.另外,从坐标变换的角度,将复制-粘贴区域的旋转、缩放变换转换成平移变换,从而实现算法的几何不变性.
2 特征提取和可疑块对定位
为了改善图像分块的不确定性,本文定义灰度级别和区域的灰度结构,并据此定位可疑块对.
灰度级别:设X为灰度图像I的数据矩阵,通过X1=X/L可将I分成L(L=1,2,3,…)个灰度级别,且灰度级别为l(0≤l≤L-1)的图像块对应的实际灰度值区间为:[0+(256/L)×l,(256/L)-1+(256/L)×l].假设L=16,灰度级别和对应的灰度值范围如表1所示.

表1 灰度级别和对应的灰度值范围
灰度结构:图像I被划分为L个灰度级别,其中灰度级别为l的图像块中包括256/L个灰度值,每个灰度值对应的像素个数组成一个向量s,称为该图像块的灰度结构.
设待检测图像I为灰度图像,图像块a属于I中被复制的区域,图像块b属于相应的粘贴区域.那么,a、b之间的灰度级别和灰度结构满足如下关系:(1)如果b是对a经过简单的复制-移动-粘贴得到的,那么b与a具有相同的灰度级别和灰度结构.(2)如果b是对a经过复制-旋转-粘贴得到的,那么b与a具有相同的灰度级别和灰度结构.(3)如果b是对a经过复制-缩放(或旋转并缩放)-粘贴得到的,那么b与a具有相同的灰度级别和满足比例关系的灰度结构.
基于此,本文首先将待检测图像I划分为L个灰度级别;然后,查找位置相邻且灰度级别相同的像素,构成图像块;最后,计算每个图像块的灰度结构,按照灰度级别和灰度结构的相似性度量定位可疑块对.
设a、b是灰度级别均为l(0≤l≤L)的两个图像块,aj+(256/L)×l和bj+(256/L)×l(0≤j≤256/L-1)分别表示a、b中灰度值为j+(256/L)×l的像素个数.于是,a和b的灰度结构s-a和s-b分别为
s-a={a0+(256/L)×l,a1+(256/L)×l,…,a256/L-1+(256/L)×l};
s-b={b0+(256/L)×l,b1+(256/L)×l,…,b256/L-1+(256/L)×l}.
设a和b中的像素总数分别为a-sum和b-sum,则a和b的灰度结构相似性度量定义为:
(1)
如果sim的值小于可疑阈值T,则说明图像块a和b的灰度结构相似,将其定位为一组可疑块对(a,b).
3 篡改区域定位
对每一组可疑块对进行基于对数极坐标变换的相位相关,以去除误匹配的可疑块,实现篡改区域的粗略定位.然后采用几何方法实现篡改区域的精确定位.
3.1 篡改区域的粗略定位
对各组可疑块对进行基于对数极坐标变换的相位相关,去除误匹配的可疑块,并计算出旋转角度、缩放尺度和位移量,作为可疑块对的特征向量.根据可疑块对的特征向量判断两两可疑块对的相似性,对相似的可疑块对进行合并分组,实现篡改区域的粗略定位.
首先,为了进行对数极坐标变换,确定可疑块的变换中心.
可疑区域的灰度结构中边界像素的稳定性较差,使得计算结果不够准确.因此,通过加权提高变换中心定位的准确度,根据某一像素点的灰度值定义其坐标的权值.
设a的灰度级别为l(0≤l≤L),对应的实际灰度值区间为:[0+(256/L)×l,(256/L)-1+(256/L)×l].设a中灰度值为I(x,y)的像素坐标为(x,y),则(x,y)的权值w(I(x,y))定义如下:
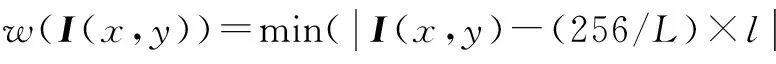
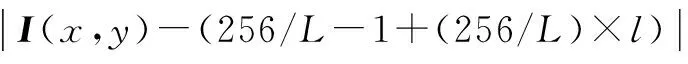
(2)
于是,可疑区域a的变换中心定义为:
(3)
其次,对每一组可疑块对进行基于对数极坐标变换的相位相关.
对笛卡尔坐标系中可疑块f(x,y)进行对数极坐标变换,设变换中心为(x0,y0),那么对应的极坐标系下的图像块f(ρ,θ)满足公式(4)所示的关系.
(4)
其中,(ρ,θ)为对应的对数极坐标系中的极径和极角.
设f1(x,y)和f2(x,y)是笛卡尔坐标系下的一组可疑块对,并且存在角度为θ0的旋转变换和参数为λ的缩放变换.则f1(x,y)和f2(x,y)之间的变换关系如公式(5)所示.f2(x,y)=f1(λ-1(xcosθ0+ysinθ0),
λ-1(-xsinθ0+ycosθ0))
(5)
设f1(lnρ,θ)和f2(lnρ,θ)分别为对应于f1(x,y)和f2(x,y)的极坐标系下的可疑块对,则由公式(4)可知,公式(5)中的变换关系在对数极坐标系下可以表示为:
f2(lnρ,θ)=f1(lnρ-lnλ,θ-θ0)
(6)
因此,笛卡尔坐标系下的旋转、缩放变换对应于对数坐标系下的平移变换,且相对平移量为(lnλ,θ0).
设F1(δ,η)和F2(δ,η)分别是f1(lnρ,θ)和f2(lnρ,θ)的傅里叶变换,则:
F2(δ,η)=F1(δ,η)e-j(δlnλ+ηθ0)
(7)
于是,f1(lnρ,θ)和f2(lnρ,θ)的互功率谱如下所示:
(8)
对P12(δ,η)进行傅里叶逆变换得到互功率谱密度Q(u,v),根据Q(u,v)在(u,v)空间的峰值分布确定可疑块对之间的相对平移量.
(1)如果f1(x,y)和f2(x,y)全部经过了复制粘贴篡改,则Q(u,v)在(u,v)空间只出现一个峰值,且峰值的位置即为这两个区域间的相对平移量(lnλ,θ0).
(2)如果f1(x,y)和f2(x,y)部分经过了复制粘贴篡改,则Q(u,v)在(u,v)空间出现多个峰值,此时,最大峰值的位置代表了这两个区域间的相对平移量.
(3)如果f1(x,y)和f2(x,y)没有经过复制粘贴篡改,则Q(u,v)在(u,v)空间将呈现不会有明显的峰值.
对每一组可疑块对计算互功率谱密度的峰值M,设相关阈值为Tq,则:(1)如果M≤Tq,舍弃该可疑块对;(2)如果M>Tq,计算旋转角度、缩放尺度和相对平移量,作为该可疑块对的特征向量.
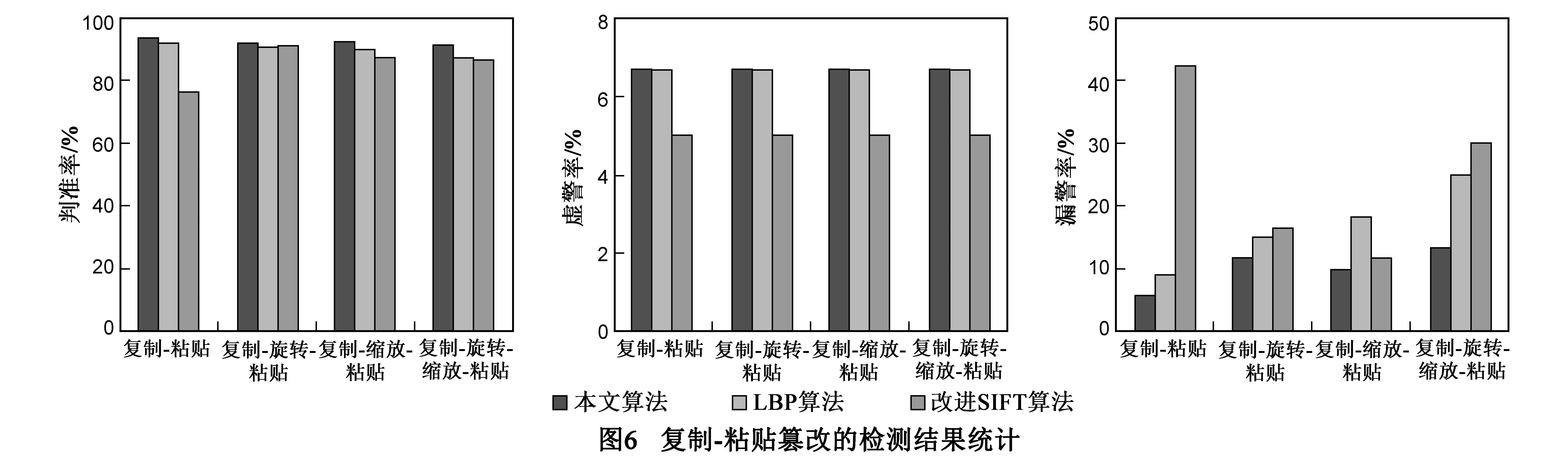
于是,经过基于对数极坐标变换的相位相关处理后,可以去除误匹配的可疑块对.
最后,对去除误匹配后的可疑块对进行合并分组,以确定复制粘贴区域的个数,并实现篡改区域的粗略定位.
如图1所示,设(A1,A1′)和(A2,A2′)是经过基于对数极坐标变换的相位相关处理后的两组可疑块对,它们的特征向量分别表示为:p1=[l1,q1,(Δx1,Δy1)];p2=[l2,q2,(Δx2,Δy2)],其欧式距离表示为:
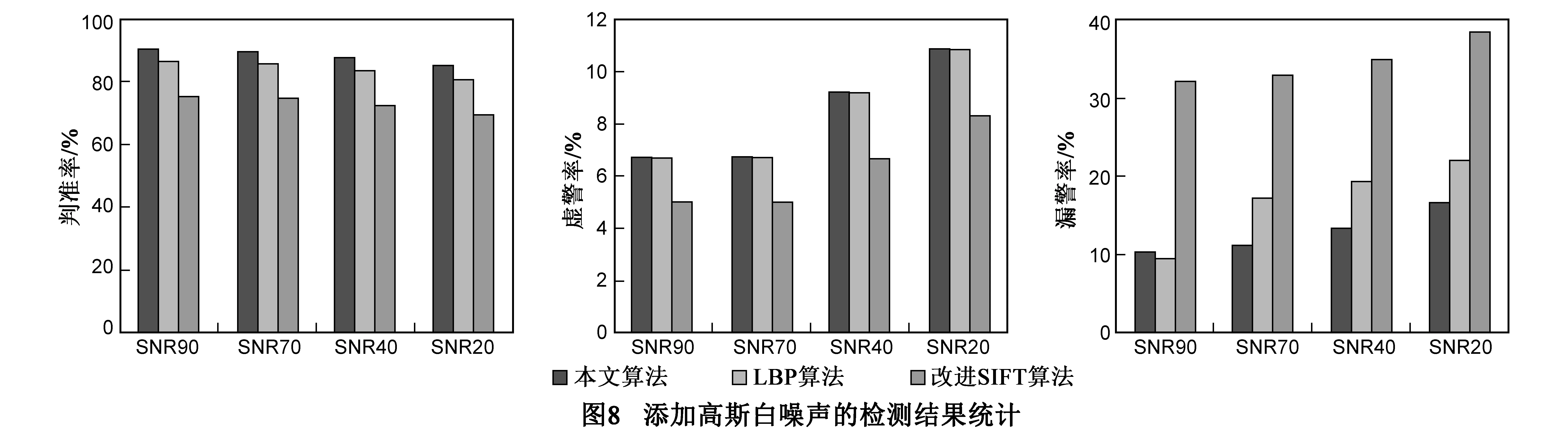
d12=‖p1-p2‖2
(9)
其中“‖·‖”表示向量的模,如果d12满足:d12≤e(0 计算两两可疑块对的特征向量的欧氏距离,并进行合并分组.最终得到的分组数与图像复制粘贴的区域数目相同,将合并后的一组称为一个粗略定位的篡改区域.3.2 篡改区域的精确定位 为了精确定位篡改区域,需要精确计算复制区域和粘贴区域之间的旋转角度、缩放尺度和相对位移量. 经过篡改区域粗略定位后,属于同一复制粘贴区域的可疑块对被合并为一组,每组包括若干可疑块对,通过可疑块对中心点之间的向量计算缩放尺度和旋转角度. 如图2所示,其中(A1,A1′)、(A2,A2′)、…、(An,An′)是粗略定位后的可疑块对,以A1的变换中心为起点,分别连接A2、A3、…、An(“n”表示可疑块对的个数)的变换中心,得到向量l12、l13、…、l1n;同样,以A1′的变换中心为起点,分别连接A2′、A3′、…、An′的变换中心,得到向量l12′、l13′、…、l1n′.于是,缩放尺度λ0可以表示为: (10) 假设向量l12、l13、…、l1n的矢量和为l,则: (11) 假设向量l12′、l13′、…、l1n′的矢量和为l′,那么: (12) 因此,l和l′的夹角即为被复制区域和粘贴区域之间的旋转角度,l的l′矢量和记为L,如图3所示,则由余弦定理可得: (13) 设(A,A′)是粗略定位后的篡改区域,(x,y)是A中的一个像素坐标,(x′,y′)是A′中与(x,y)对应的像素坐标,即(x,y)与(x′,y′)满足角度为θ0的旋转变换R、尺度为λ0的缩放变换S和相对位移量为(Δx,Δy)的平移变换H.于是,(x,y)和(x′,y′)满足如公式(14)所示的关系: (14) 由(x,y)、(x′,y′)、θ0和λ0可以计算出(Δx,Δy),计算A和A′中所有像素点坐标对应的偏移量的平均值,即得到复制区域和粘贴区域之间的相对位移量(Δx0,Δy0). 按照精确计算得到的尺度参数λ0、旋转角度θ0和相对位移量(Δx0,Δy0)进行篡改区域的精确定位. 首先,以待检测图像I的位置为基准,按照λ0和θ0对I做尺度缩放和旋转变换,按照(Δx0,Δy0)对I做平移变换,得到新图像NI1,计算I与NI1的差值图像E1;其次,按照λ0和θ0对图像I做尺度缩放和旋转的反变换,按照(Δx0,Δy0)对I做反方向的平移变换,得到新图像NI2,计算I与NI2的差值图像E2;然后,标记篡改区域:差值图像E1和E2中均存在一个像素灰度值非常小甚至接近零的区域,其中一个是被复制的区域,另一个是粘贴的区域.如果这两个区域的像素灰度值在 (-t,t)范围内,那么在一个与原图像大小相同的全0二值图像中将其对应的像素位置设为1.于是,篡改区域被标记为白色.最后,利用形态学的膨胀和腐蚀操作填充最大连通分量之间的“空洞”,实现图像中复制粘贴区域的精确定位. 仿真实验的硬件环境为:CPU 2.2GHz,3.0GB内存;软件环境为:Matlab R2012a.从Columbia大学自然图像数据库中选取120幅图像,应用PhotoShop进行复制粘贴篡改,得到60幅隐藏目标类的篡改图像,以及240幅造成假象类的篡改图像,包括不同参数的复制-粘贴、复制-旋转-粘贴、复制-缩放-粘贴和复制-旋转-缩放-粘贴的图像各60幅.并且对篡改图像进行模糊、高斯白噪声及JPEG压缩等后处理,构成图像数据库. 4.1 评价指标及参数设置 设测试图像库中篡改图像数为Ne,可信图像数为Nt,经本文算法检测认为被篡改过且确实被篡改的图像数为Ne1,经本文算法检测认为被篡改过但实际可信的图像数为Nt1,经本文算法检测认为没有被篡改过且确实可信的图像数为Nt2,经本文算法检测认为没有被篡改过但实际被篡改的图像数为Ne2,算法的判准率、虚警率和漏警率分别定义如下: 判准率=((Ne1+Nt2)/ (Ne+Nt))×100%; 虚警率=(Nt1/Nt)×100%; 漏警率=(Ne2/Ne)×100%. 经过多次实验调试,实验中的参数设置如下: (1)灰度级别参数L=16,即将待检测图像分成16个灰度级别;(2)经过多次试验,设置可疑阈值T=0.06;即如果两个图像块的相似性sim小于0.06,则认为它们是一组可疑块对;(3)相关阈值Tq=0.05,即对每一组可疑块对做基于对数极坐标变换的相位相关时,如果互功率谱密度的峰值M大于相关阈值0.05,则将该可疑块对粗略定位为篡改区域;(4)篡改区域精确定位时,像素灰度值范围(-t,t)=(-5,5),即将像素灰度值在(-5,5)内的区域标记为白色. 4.2 算法有效性实验 本节从隐藏目标类篡改和造成假象类篡改两方面来验证本文算法的有效性. (1)隐藏目标类实验 隐藏目标类的复制-粘贴篡改,主要是复制图像中的背景区域来覆盖某一目标.如图4所示为隐藏目标类篡改的检测结果,其中图4(a1)~(d1)为原始图像,(a2)~(d2)为篡改图像,(a3)~(d3)为检测结果,图4(a2)为单一的复制-粘贴篡改,图4(b2)为篡改图像进行模板尺寸为3×3、方差为1的高斯模糊,图4(c2)为篡改图像添加信噪比SNR为70的高斯白噪声,图4(d2)为篡改图像进行质量因子为70的JPEG重压缩. 由图4可知,对于隐藏目标类的复制-粘贴篡改,无论是复制背景目标隐藏前景目标(图4(a2))、还是复制背景隐藏目标(图4(b2)~(d2)),本文算法均能有效定位篡改区域,虽然检测结果中存在漏匹配的图像块,但是检测到的图像块已经构成了能够足够定位篡改区域的联通区域. (2)造成假象类实验 造成假象类的复制-粘贴篡改,主要是复制图像中的某一个目标并粘贴到图像中另一个区域,以造成某种假象.如图5所示为造成假象类篡改的检测结果,其中图5(a1)~(e1)为原始图像,(a2)~(e2)为篡改图像,(a3)~(e3)为检测结果,(a2)为经过逆时针30°旋转的复制-旋转-粘贴篡改,(b2)为经过0.75倍等比缩放的复制-缩放-粘贴篡改,(c2)为篡改图像进行模板尺寸为3×3、方差为1的高斯模糊,(d2)为篡改图像添加信噪比SNR为70的高斯白噪声,(e2)为篡改图像进行质量因子为70的JPEG重压缩. 由图5可知,对于造成假象类的复制-粘贴篡改,本文算法能够有效抵抗旋转、缩放变换,表现出了几何不变性.而且,本文算法根据像素灰度级别进行图像分块,并结合灰度结构定位可疑块对,因此,本文算法不限制篡改区域的大小.如图5(a2)所示,对于较小的篡改区域该算法仍然有效. 4.3 算法性能对比分析 本文从图像块匹配的角度实现了具有几何不变性的复制粘贴盲鉴别算法,已有的基于图像块匹配的盲鉴别算法中,文献[14]中算法(LBP算法)对于旋转变换及模糊、噪声和JPEG重压缩等具有较强的鲁棒性.文献[17]中算法(改进SIFT算法)对基于传统SIFT特征点匹配的盲鉴别算法进行了改进,去除了误匹配.因此,为了对比分析算法抵抗几何变换和后处理操作的鲁棒性,基于本文图像数据库,对本文算法、LBP算法和改进SIFT算法的判准率、虚警率和漏警率进行统计分析.本文实验设置如下:(1)复制-粘贴的测试统计;(2)算法鲁棒性的测试统计. (1)复制-粘贴的测试统计 本文实验中对图像的复制-粘贴操作包括四种:(Ⅰ)单一的复制-粘贴篡改,共120幅测试图像,包括60幅隐藏目标类的篡改图像和60幅造成假象类的篡改图像;(Ⅱ)不同角度的复制-旋转-粘贴篡改,共60幅测试图像;(Ⅲ)不同尺度的复制-缩放-粘贴篡改,共60幅测试图像;(Ⅳ)不同角度和尺度的复制-旋转-缩放-粘贴篡改,共60幅测试图像.其中(Ⅱ)、(Ⅲ)、(Ⅳ)类测试图像不包括隐藏目标类的篡改.以上复制-粘贴图像与120幅自然图像构成测试样本集,应用本文算法、LBP算法和改进SIFT算法进行检测,判准率、虚警率和漏警率的统计结果如图6所示. 由图6中数据可知: (a)对于单一的复制-粘贴篡改,本文算法和LBP算法对隐藏目标类的篡改和造成假象类的篡改均能取得较高的判准率和较低的漏警率,但是其虚警率较高,原因是这两个算法将大背景的自然图像(比如以蓝天和大海构成的场景图像)误判为复制-粘贴的图像块.但是本文算法仍然优于LBP算法,判准率为93.75%、虚警率为6.67%、漏警率为5.83%.改进SIFT算法的判准率较低,这是因为对于隐藏目标类的篡改,基于特征点匹配的方法表现出了较明显的弱势. (b)对于复制-旋转/缩放-粘贴篡改,本文算法的判准率均高于LBP算法和改进SIFT算法,而且其漏警率也较低.说明本文算法抵抗旋转、缩放等变换的性能优于LBP算法和改进SIFT算法. (2)算法鲁棒性的测试统计 对120幅自然图像和以上复制-粘贴测试中的300幅篡改图像,分别进行如下处理:①高斯模糊,模板尺寸为3×3,滤波器方差分别为0.5、1、1.5和2.②添加高斯白噪声,信噪比SNR分别为90、70、40和20.③JPEG重压缩,质量因子分别为90、70、50和30.应用本文算法、LBP算法和改进SIFT算法对以上图像进行检测,统计判准率、虚警率和漏警率,结果分别如图7~图9所示. 由图7~图9中数据可知: (a)对于高斯模糊、高斯白噪声和JPEG重压缩,本文算法的判准率均高于LBP算法和改进SIFT算法,其虚警率与LBP算法相当、高于改进SIFT算法,但其漏警率表现出了明显优势,说明本文算法对后处理操作具有较强的鲁棒性. (b)改进SIFT算法的漏警率明显高于本文算法和LBP算法,其主要原因仍然是改进SIFT算法对于隐藏目标类篡改检测所表现出的弱势. 结合算法有效性实验中的结果可知,本算法不但具有旋转、缩放不变性,而且针对模糊、噪声和JPEG重压缩等操作,具有较强的鲁棒性.另外,本算法的综合检测性能优于LBP算法和改进SIFT算法. 4.4 算法时间复杂度分析 时间复杂度反映了算法的执行效率,是评价算法性能的一个重要指标.假设图像大小为M×N,下面从本文算法的主要实现步骤对其时间复杂度进行分析:(1)提取像素的灰度级别和灰度结构特征,并定位可疑块对,设定位出的可疑块对的数目为s(s 本文算法总的时间复杂度为: max(O(MN),O(M1N1),O(s)×O(snlogn),O(s12),O(s12))=O(MN). 针对常用的图像“复制-旋转/缩放-粘贴”篡改,本文提出了具有几何不变性的基于图像块匹配的复制-粘贴盲鉴别算法.主要贡献为:(1)定义灰度级别和灰度结构,并将其作为特征划分图像的可疑块对,改善了图像分块不确定的问题;(2)结合对数极坐标变换和相位相关的思想,将笛卡尔坐标系下篡改区域的检测转换为极坐标系下图像中可疑块对的匹配;(3)本文提出的复制-粘贴盲鉴别算法能够有效地检测并定位经过旋转、缩放变换的篡改区域,而且能够抵抗模糊、高斯白噪声和JPEG重压缩等后处理.并且,算法的时间复杂度为O(MN),其数量级仅为线性阶. 图像区域的复制粘贴操作是一种简单且常用的篡改手段,由于同一幅图像中的颜色、纹理等特征的相似度较大,因此,复制粘贴篡改后的图像很难引起视觉上的差异,而且,复制区域旋转、缩放等变换和篡改图像的后处理操作,使得其更能达到以假乱真的效果.但是,图像鉴别技术发展的同时,造假者也在研究更加高级的篡改手段,而且一幅伪造图像往往会综合利用多种篡改手段,因此,需要进一步研究相应的检测技术.因此,数字图像盲鉴别技术既有很大的创新空间又面临着更大的挑战. [1]周琳娜,张茹,郭云彪.数字图像内容取证[M].北京:高等教育出版社,2011. [2]周琳娜,王东明,郭云彪,杨义先.基于数字图像边缘特性的形态学滤波取证技术[J].电子学报,2008,36(6):1047-1051. Zhou Lin-na,Wang Dong-ming,Guo Yun-biao,Yang Yi-xian.Exposing digital forgeries by detecting image blurred mathematical morphology edge[J].Acta Electronica Sinaca,2008,36(6):1047-1051. (in Chinese) [3]王波,孙璐璐,孔祥维,尤新刚.图像伪造中模糊操作的异常色调率取证技术[J].电子学报,2006,34 (S1):2451-2454.Wang Bo,Sun Lu-lu,et al.Image forensics technology using abnormity of local hue for blur detection[J].Acta Electronica Sinaca,2006,34 (S1):2451-2454. (in Chinese) [4]B Wang,XW Kong,B Elisa et al.,Exposing Copy-Paste-Blur forgeries based on color coherence[J].Chinese Journal of Electronics,2009,18(3):487-490. [5]Fridrich J,Soukal D,Lukáš J.Detection of copy-move forgery in digital images[A].Proceedings of Digital Forensic Research Workshop[C].Cleveland:IEEE Press,2003. http://ws2.binghamton.edu/fridrich/Research/copymove.pdf. [6]Wang X F,Zhang X N,Li Z,et al.A DWT-DCT based passive forensics method for copy-move attacks[A].Third International Conference on Multimedia Information Networking and Security (MINES)[A],Shanghai:IEEE Press,2011. 304-308. [7]Cao Y J,Gao T G,Li F,et al.A robust detection algorithm for copy-move forgery in digital images[J].Forensic Science International,2012,214(1):33-43. [8]Hu J,Zhang H,Gao Q.An improved lexicographical sort algorithm of copy-move forgery detection[A].Second International Conference on Networking and Distributed Computing (ICNDC) [C].Beijing:IEEE Press,2011. 23-27. [9]Popescu A C,Farid H.Exposing digital forgeries by detecting duplicated image regions[R].TR2004-515 Department of Computer Science,Dartmouth College,Hanover,New Hampshire,USA,2004. [10]Mahdian B,Saic S.Detection of copy-move forgery using a method based on blur moment invariants[J].Forensic Science International,2007,171(2):180-189. [11]Ryu S J,Lee M J,Lee H K.Detection of copy-rotate-move forgery using Zernike moments[A].12th International Conference on Information Hiding[C].Canada:Springer Press,2010. 51-65. [12]Ryu S J,Kirchner M,Lee M J,et al.Rotation invariant localization of duplicated image regions based on zernike moments[J].IEEE Transactions on Information Forensics and Security,2013,8(8):1355-1370. [13]Liu G,Wang J,Lian S.A passive image authentication scheme for detecting region-duplication forgery with rotation[J].Journal of Network and Computer Applications,2011,34(5):1557-1565. [14]Davarzani R,Yaghmaie K,Mozaffari S,et al.Copy-move forgery detection using multiresolution local binary patterns[J].Forensic Science International,2013,231(1):61-72. [15]Leida Li,Shushang Li,Hancheng Zhu,Xiaoyue Wu.Detecting copy-move forgery under affine transforms for image Forensics[J].Computers & Electrical Engineering,2014,40(6):1951-1962. [16]Huang H J,Guo W Q,Zhang Y.Detection of copy-move forgery in digital images using SIFT algorithm[A].IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application[C].Wuhan:IEEE Press,2008. 272-276. [17]Amerini I,Ballan L,Caldelli R,et al.A SIFT-based forensic method for copy-move attack detection and transformation recovery[J].IEEE Transactions on Information Forensics and Security,2011,6(3):1099-1110. [18]Xu B,Wang J W,Liu G J.Image copy-move forgery detection based on SURF[A].IEEE International on Multimedia Information Networking and Security[C].Nanjing:IEEE Press,2010. 889-892. [19]Guo J M,Liu Y F,Wu Z J.Duplication forgery detection using improved DAISY descriptor[J].Expert Systems with Applications,2013,40(2):707-714. [20]Hashmi M F,Anand V,Keskar A G.Copy move image forgery detection using an efficient and robust method combining un-decimated wavelet transform and scale invariant feature transform[J].Aasri Procedia,2014,9:84-91. [21]Jian Li,Xiaolong Li,Bin Yang,and Xingming Sun.Segmentation-based image copy-move forgery detection scheme[J].IEEE Transactions on Information Forensics and Security,2015,10(3):507-518. [22]Ewerton Silva,Tiago Carvalho,Anselmo Ferreira,Anderson Rocha.Going deeper into copy-move forgery detection:Exploring image telltales via multi-scale analysis and voting processes[J].Journal of Visual Communication and Image Representation,2015,29:16-32. 吕颖达 女,1983年生于河北文安.吉林大学计算机科学与技术学院博士.研究方向为图像处理、数字图像取证及模式识别. 申铉京 男,1958年生于吉林和龙.吉林大学计算机科学与技术学院教授、博士生导师.研究方向为多媒体技术、图像处理和智能检测系统. 陈海鹏(通信作者) 男,1978年生于山东曹县.吉林大学计算机科学与技术学院副教授.研究方向为多媒体技术、图像处理和信息安全. E-mail:chenhp@jlu.edu.cn Blind Forensic for Image Copy-Paste Tampering with Geometric Invariance LÜ Ying-da1,2,3,SHEN Xuan-jing1,2,CHEN Hai-peng1,2 (1.CollegeofComputerScienceandTechnology,JilinUniversity,Changchun,Jilin130012,China;2.KeyLaboratoryofSymbolicComputationandKnowledgEengineeringofMinistryofEducation,JilinUniversity,Changchun,Jilin130012,China;3.CenterforComputerFundamentalEducation,JilinUniversity,Changchun,Jilin130012,China) A blind identification algorithm for image copy-paste tampering with geometric invariance was proposed in this study.Firstly,gray level and gray structure are defined,the image is divided into blocks according to the gray levels of pixels,and the suspicious blocks in the image is positioned through the gray structure;Secondly,phase correlation is made for each group of suspicious block based on logarithm polar coordinate transformation,and the tampering regions are located preliminarily;Finally,the rotation angle,scale and translation measurements are calculated precisely,and the tampering regions are positioned.The experimental results show that our algorithm performs well against copy-rotate/scale-paste tampering,and its detection efficiency and robustness are better than the existing algorithms. blind forensic;copy-paste tampering;logarithm polar coordinate transformation;phase correlation 2015-04-23; 2015-07-03;责任编辑:蓝红杰 国家自然科学基金(No.61305046);吉林省自然科学基金(No.20140101193JC,No.20130522117JH,No.20150101055JC) TP391 A 0372-2112 (2016)11-2592-08 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.11.005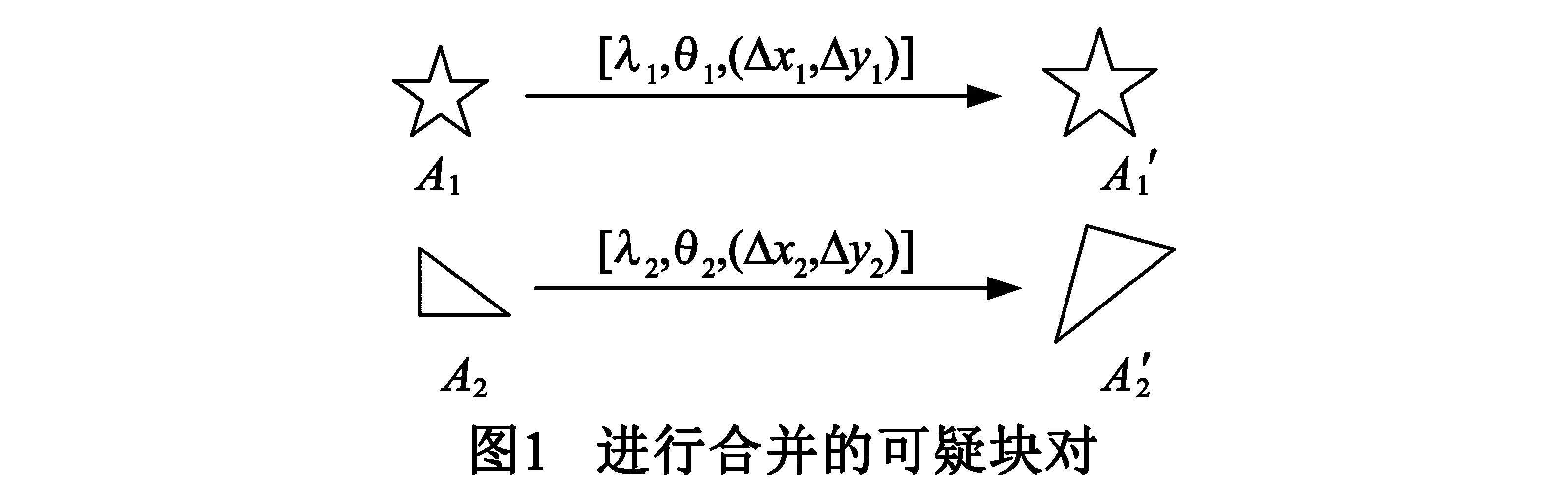


4 实验结果及算法分析




5 结论



