单接收天线空时分组码系统的分层调制识别
凌 青,张立民,闫文君,邓向阳
(海军航空工程学院信息融合所,山东烟台 264001)
单接收天线空时分组码系统的分层调制识别
凌 青,张立民,闫文君,邓向阳
(海军航空工程学院信息融合所,山东烟台 264001)
针对单接收天线空时分组码系统的调制识别问题,提出了一种基于初等四阶累积量的分层调制盲识别算法. 首先推导了不同信号星座在无噪声条件下的初等四阶累积量的理论值和方差,然后根据最大似然比检测求得阈值;最后比较接收信号初等四阶累积量实验值与阈值的大小盲识别调制方式. 该算法不需要信道、噪声功率等先验信息,适合非合作通信场合. 仿真结果表明,所提出的算法在低信噪比下能够较好的识别单接收天线空时分组码调制方式.
空时分组码;调制识别;单接收天线;初等四阶累积量
1 引言
在非合作通信场合,获取截获信号的信号参数是信号检测和信号解码的中间环节. 其中信号参数包括调制信息、信道信息和信道编码信息,获取截获信号的调制信息能够为后续的信号盲处理提供先决条件. 空时分组码是现代无线通信中非常实用的技术,它旨在达到Multiple Input Multiple Output(MIMO)信道的理论信息容量. 因此,空时分组码系统的调制识别是非合作MIMO通信的重要内容之一.
目前,主流的调制识别算法主要分为最大似然的识别方法[1~6]和基于特征提取的识别方法[7~10]. 其中最大似然的方法给出了正确识别概率的上界,然而识别过程需要预先知道信道矩阵或复合信道矩阵,且对高阶调制计算复杂度较高,不适合全盲场合. 基于特征提取是从接收信号中提取特征参数,根据特征参数盲识别调制方式. 文献[5~10]主要针对MIMO系统的调制识别,而对空时分组码系统的调制识别研究较少. 此外,在实际的应用中,由于天线尺寸、功率和造价等限制,单接收天线更受青睐. 因此研究单接收天线的空时分组码的调制识别具有实用价值.
本文在单接收天线条件下提出一种新的有效的调制盲识别算法,该方法具有以下优点:
(1)适用于单接收天线系统.
(2)不需要预先知道信道信息、噪声信息.
(3)识别算法的计算的复杂度低,为O(N).
(4)适用于不同的空时分组码.
2 信号模型与假设
考虑具有Nt个发射天线1个接收天线的线性STBC通信系统,每组码中需要传输的符号数为N,每组的符号通过L时隙进行传输,则STBC码矩阵维数为Nt×L,定义为C(S):
(1)其中{Ak,Bk}是给定的Nt×L维码字矩阵,R(sk)和s(sk)分别代表sk的实部和虚部,S=[s1,s2,…,sN]是经调制后的某组码待传输符号,且调制星座具有M个状态.
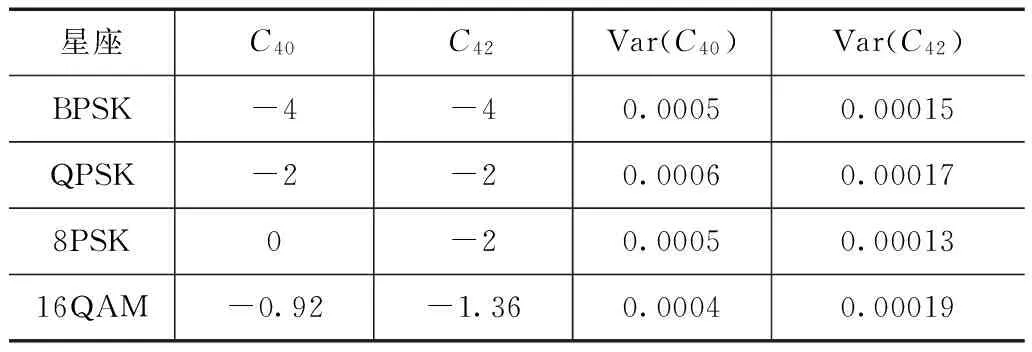
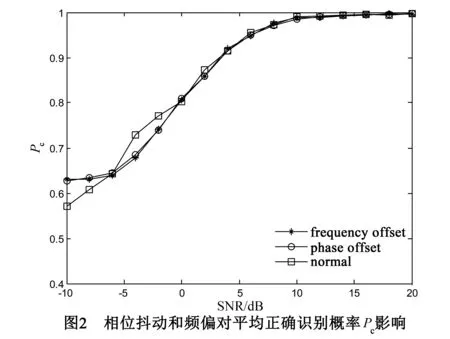
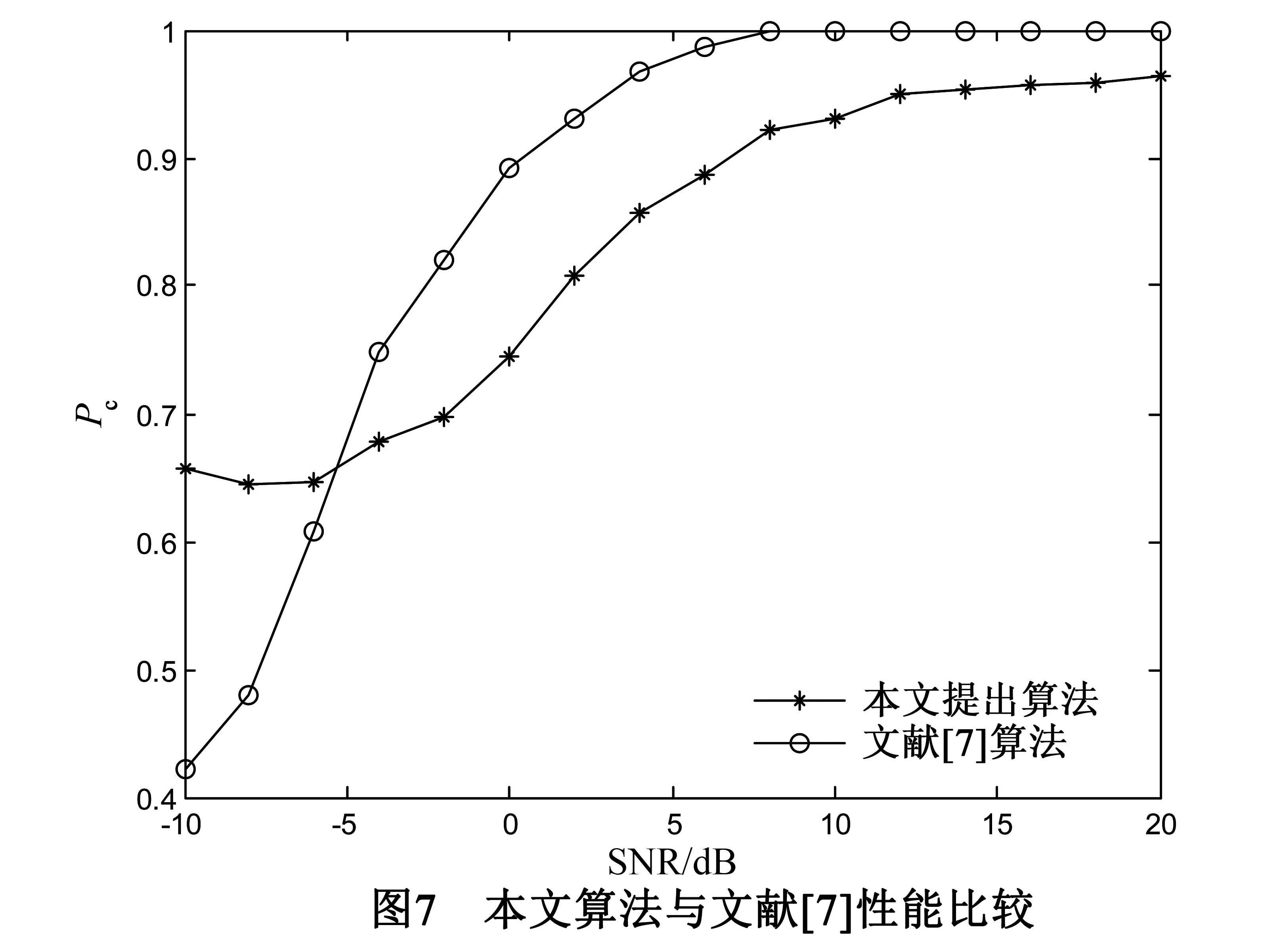
假定信号S为经过相同线性调制方式后的调制信号,且独立同分布. 传输信号S的能量为1. 假设第一列接收信号为y(0),空时分组码的第k+1组截获的信号为y(k),其中0≤k y(k)=HS(k)+w(k) (2) 3.1 定义 四阶累积量定义两种形式: C40=cum(y(n),y(n),y(n),y(n)) (3) C42=cum(y(n),y(n),y*(n)y*(n)) (4) 3.2 估计值 在信号处理的实际应用中,信号的四阶累积量需要从有限长度的接收信号中估计. 假定y(n)是零均值,四阶累积量可以表示为: (5) (6) 3.3 四阶累积量理论值和方差推导 空时分组码系统中不同星座的信号,由式(3),(4)可以计算四阶累积量的理论值. 假定所有星座符号是等概率发送的,理论值是无噪声的星座符号的总体平均值. 对于QAM和PSK星座,C20=0,C21是信号能量. 计算方差分两种情况讨论: 情况1 在C21已知的条件下,累积量的估计是无偏估计,因此: (7) (8) (9) (10) 情况2 在C21未知的条件下,对累积量的估计是有偏估计,因此: (11) (12) (13) (14) (15) (16) 由式(13)~(15),(12)可以表示为: (17) 空时分组码系统中,不同星座符号的理论值和方差如表1. 表1 不同星座符号四阶累积量的理论值和方差 3.4 阈值的求法 H0:T∈[a-b,a+b]H1:T∉[a-b,a+b] 其中: (18) (19) ξ=(μ0+μ1)/2 (20) 3.5 联合检测算法 (1)识别不同调制方式的性能 在h(n)=δ(n)、没有频偏和相位抖动且噪声为零均值的复高斯的理想的条件下,BPSK,QPSK,8PSK和16QAM正确识别概率的曲线如图1所示. 由图1可以看出,BPSK,QPSK,8PSK和16QAM的识别概率随着信噪比提高而提高,这是由于在低信噪比下,噪声会对四阶累积量的估计值产生较大的误差,从而影响算法的性能. (2)相位抖动和频偏 (4)采样数K对算法影响 在信道为频率平坦的Nakagami-m信道且m=3,采样数为K∈{1024,2048,4096,8192}时平均识别概率的变化如图4所示. 算法的平均识别概率在采样数为8192时效果最理想,原因是低样本数不利于抑制噪声和信道对C42和C40的估计值的影响,导致算法在低样本数量性能劣于高样本数量. (5)非高斯噪声下算法性能 样本的抽样数设为K=1024和K=2048,信道为频率平坦的Nakagami-m信道且m=3. 如图5所示,其中Gaussian和NonGaussian分别代表高斯噪声和非高斯噪声条件下曲线. 由图5可以看出,高斯噪声环境和非高斯噪声环境对算法没有太大影响,因此算法适用于非高斯噪声环境下识别. (6)不同STBC算法的性能比较 在K=1024和频率平坦的Nakagami-m信道且m=3条件下,比较算法在SM、Al、ST3和ST4空时分组码的性能,其中SM、Al、ST3和ST4编码矩阵见文献[12]. 由图6可以观察,这四种STBC下调制识别性能差别不大. (7)与其他算法性能比较 将本文算法与仅有的一篇研究单接收天线的调制识别算法作比较[7],取采样数K=512,采用Al编码方式,噪声为零均值高斯白噪声,如图7所示.从图7可以看出,算法的性能在SNR<-4dB时,本文提出的算法优于文献[7]的算法,但在SNR>-4dB时,文献[7]的算法优于本文提出的算法,大约性能提高10%左右. 但是文献[7]采用的是最大似然的算法,需要事先知道信道的系数,在非合作场合并不适应,而本文提出的算法最大的正确识别概率也能达到96.48%,能够满足实际应用. (8)算法的复杂度分析 算法的复杂度包括四阶抽样累积量的计算和与阈值的比较. 四阶抽样累积量的计算如式(6)所示,实质就是一个嵌套的两层循环. 在外层循环的控制下,它的循环体的渐进时间为O(N),其中包括一个内层循环;在内层循环的控制下,它所包含的乘法操作的渐进时间为O(1),因此该程序段的渐进时间复杂度为O(N×1). 与阈值的比较计算复杂度为Ο(1),因此算法的计算复杂度为O(N). 在Nakagami-m信道且m=3,K=512和Al编码的条件下识别BPSK调制方式,算法在intel i5处理器主频为1.8GHz的计算机上计算时间为0.014s. 本文提出了一种在单天线条件下调制方式盲识别算法. 算法分别在不同采样数、不同信道参数、不同STBC、不同的相位抖动和不同载波频偏的条件下进行了仿真,并讨论了算法在非高斯噪声下的性能,最后将本文算法与仅有的一篇单接收天线下的文献进行了比较. 仿真结果表明,本文提出的算法适合非合作通信且算法性能较好. [1]Choqueuse V, Azou S, Yao K. Blind modulation recognition for MIMO system[J]. MTA Review, 2009, 19(2): 183-196. [2]Wei W, Larimore M G. A new maximum-likelihood method for modulation classification[A]. 1995 Conference Record of the Twenty-Ninth Asilomar Conference[C]. Pacific Grove: IEEE Computer Socity Washington, 1995. 1132-1135. [3]Muhlhaus M, Oner M, Dobre O A. A low complexity modulation classification algorithm for MIMO systems[J]. IEEE Communications Letters, 2013, 17(10):1881-1884. [4]Luo M, Li L, Tang B. A blind modulation recognition algorithm suitable for MIMO-STBC systems[A]. International Conference on Communications and Information Technology[C]. Chengdu: IEEE, 2012. 271-276. [5]Luo M, Li L, Qian G. A blind modulation identification algorithm for STBC systems using multidimensional ICA[J]. Concurrency and Computation: Practice and Experience, 2013, 26(8):1490-1505. [6]钱国兵,李立萍,郭亨艺. 多入单出正交空时分组码系统的调制识别[J]. 电子信息学报,2013,35(1):185-190.Qian Guobing, Li Liping, Guo Hengyi. Modulation identification for orthogonal space-time block code in multiple input single output systems[J]. Journal of Electronics & Information Technology, 2013, 35(1): 185-190. (in Chinese) [7]吴月娴,葛临东,许志勇. 常用数字调制信号识别的一种新方法[J]. 电子学报,2007,35(4):782-785. Wu Yuexian, Ge Lindong, Xu Zhiyong. A novel identification method for commonly used digital modulations[J]. Acta Electronica Sinica,2007, 35(4): 782-785. (in Chinese) [8]Hassan K, Dayoub I, Hamouda W. Blind digital modulation identification for spatially-correlated MIMO systems[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 683-693. [9]Muhlhaus M, Oner M, Dobre O A. Automatic modulation classification for MIMO systems using fourth-order cumulants[A]. Vehicular Technology Conference[C]. Quebec City: IEEE, 2012. 1-5. [10]Marey M, Dobre O A. Blind modulation classification algorithm for single and multiple-antenna systems over frequency-selective channels[J].IEEE Signal Processing Letters, 2014, 21(9): 1098-1102. [11]Alamouti S. A simple transmit diversity technique for wireless communication[J]. IEEE Journal on Selected Areas in Communication, 1998, 48(7):1451-1458. [12]Choqueuse V, Yao K, Collin L, Burel G. Hierarchical space-time block code recognition using correlation matrices[J]. IEEE Transactions on Wireless Communication, 2008, 7(9):3526-3534. 凌 青 女,1987年出生,湖南衡阳人,海军航空工程学院信息融合所博士研究生,研究方向为空时分组码检测、MIMO技术. E-mail: linqing19870522@163.com 张立民(通信作者) 男,1966年出生,辽宁开原人,教授,2005年获天津大学信号与信息处理专业博士学位,现为海军航空工程学院信息融合所教授,研究方向为卫星信号处理、武器系统仿真等. E-mail:iamzlm@163.com Hierarchical Modulation Classification of Space-Time Block Codes with a Single Receive Antenna LING Qing,ZHANG Li-min,YAN Wen-jun,DENG Xiang-yang (InstituteofInformationFusion,NavalAeronauticalandAstronauticalUniversity,Yantai,Shandong264001,China) A method for blind classification of Space-Time Block Codes (STBCs) with a single receive antenna based on elementary fourth-order cumulants is proposed. Firstly,the theoretical values and variance of various signal constellations were obtained by computing the ensemble averages over the ideal noise-free constellation. And then the thresholds were gained by the likelihood ratio test (LRT) for the tests in the hierachical classification scheme. Finally,the automatic classification of modulation scheme was realized by comparing the experimental values and the thresholds. Furthermore,unlike other methods,this algorithm does not require any prior information of the channel coefficients,and noise power and,consequently,is well-suited for non-cooperative context. The simulation shows that the proposed algorithm performs well even at a low signal to noise ratio (SNR). space-time block codes (STBCs);modulation classification;single receiver antenna;elementary fourth-order cumulants 2015-07-03; 2015-09-29;责任编辑:马兰英 国家自然科学基金(No.61102167);泰山学者工程专项经费资助 TN911.7 A 0372-2112 (2016)11-2802-05 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.11.033
3 基于四阶累积量的调制识别




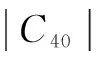



4 仿真和结果








5 总结



