区间信度结构下的证据合成方法研究
孙伟超,许爱强,李文海
(1.海军航空工程学院研究生管理大队,山东烟台 264001;2.海军航空工程学院飞行器检测与应用研究所,山东烟台 264001)
区间信度结构下的证据合成方法研究
孙伟超1,许爱强2,李文海2
(1.海军航空工程学院研究生管理大队,山东烟台 264001;2.海军航空工程学院飞行器检测与应用研究所,山东烟台 264001)
在使用证据理论进行数据融合的过程中,有时精确的信度结构很难获得,此时需要对区间信度进行合成.本文分析了在DST和DSmT框架下的区间证据合成问题,对目前使用的方法进行了简要的回顾.通过对优化方法进行研究,提出了4种应用于区间信度组合的优化方法.CDI1~CDI4方法都可应用于DST和DSmT框架,对不精确,不确定以及冲突的信息进行合成,合成结果准确度逐步提高.文章最后给出了算例验证,并与其他区间信度合成方法的进行对比.
区间信度结构;DSmT理论;证据组合规则
1 引言
信息的不完整和信息的缺失,会造成信息的不确定性.区间信度结构通过利用区间数来为辨识框架上的元素赋值,可以有效地表现不确定性信息.但是在证据组合的过程中,经典的证据理论需要精确的置信度与置信结构,面对区间信度结构,经典的证据组合规则无法使用.为了拓展证据理论的使用领域,近年来,国内外许多学者展开了区间证据合成方法的研究.
E.S.Lee和Q.Zhu[1]最早对区间证据合成方法进行了研究,定义了广义加与广义乘两种区间基本运算,并基于此给出区间证据合成公式.Denux[2,3]构建了二次规划模型以单值形式合成区间证据,从而取代之前方法中采用的区间算术方法,同时给出了区间证据有效性准则和正规化准则.以上两种方法仅局限于Smets提出的可传递信度模型(TBM)框架[4]下的单元区间信息的组合.Wang等[5]对Denux方法进行改进,在DST框架下提出区间证据组合最优化方法.针对Wang方法在冲突证据合成时可能出现的失效问题,陈圣明[6]通过相对权重对证据进行修改.康兵义[7]等提出了一种区间信度赋值产生方法.F.Smarandache和J.Dezert[8]给出了在DSmT框架下不精确信度融合方法.
到目前为止,大部分区间证据合成方法产生于TBM框架和DST框架,应用范围有限,而目前应用在DSmT框架下的方法由于基于集合运算思想,导致结果是次优的.因此,证据理论中的区间信度组合问题仍没有完全解决.本文将首先对证据理论做简要介绍,在对F.Smarandache和J.Dezert提出的不精确信度融合方法进行分析的基础上,研究如何对区间组合问题进行优化,提出新的区间信度组合方法.
2 证据理论概述
Dempster-Shafer理论[9](D-S理论)采用集合表达命题.对于需要判决的问题,由所有可能答案组成的集合Θ表示.Θ={θ0,θ1,…θn}作为该融合问题的辨识框架,含有n个完备且相互排斥的命题θi.


Dempster组合规则在合成不确定信息方面有广泛的应用,但也存在一些缺点与局限性.表现在其缺乏完整的理论证明,且在面对高冲突情况时失效等方面.为了克服Dempster组合规则的局限性,有许多学者在Shafer模型下提出了新的组合规则.其中包括析取规则[10,11],Murphy组合规则[12],Smets组合规则[13],Yager组合规则[14],Dubios-Prade组合规则[15]等.Smets在文献[11]中对这些组合规则进行了比较分析,Leferve等[16]提出了统一框架,将这些规则以相同的组合机制纳入到框架中.
Dezert-Smarandache Theory (DSmT)[17]可以看作是经典D-S理论的推广,但它们又存在着重要的差异.DSmT可以不受DST框架限制,处理不确定,高冲突和不精确证据源的静态或动态融合问题.


混合DSm组合规则是经典DSm组合规则的广义化,在处理具有精确广义基本信度赋值的问题时,该规则可以用于任何模型,包括自由DSm模型,Shafer模型以及任何其他的混合模型[18].除此之外,比例冲突重分配规则(PCR规则)[19,20]也可用于任何模型.目前PCR规则有共6个版本[21,22],其区别也在于对冲突质量的重新分配方式.
3 目前存在的区间证据合成方法
目前,面对区间信度结构IBS(Interval-valued Belief Structures)上的证据合成问题,在DST框架下,上文提到的Lee和Zhu、Denux、Yager、Wang等人都给出了自己的合成方法,在文献[5]中有以上各方法的对比分析,本文不再赘述;在DSmT框架下,Smarandache和Dezert将精确信度结构上定义的DSm组合规则扩展到区间信度结构上.用(A)和(A)来表示用于区间的DSm组合规则得到的结果.在进行区间证据合成时,对于所有的A∈DΘ,混合DSm组合规则表示如下:



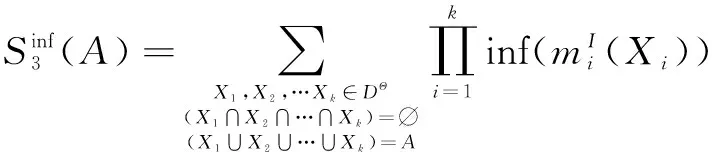
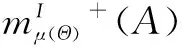

4 区间信度融合方法
针对以上问题,本文通过对PCR规则进行分析,认可其将冲突质量重新进行分配的思想;同时,考虑到区间运算对区间基本信度赋值两端点进行运算,会割裂其内在联系,造成结果误差,故本文使用最优化方法替代区间运算,提出4种广义幂集框架下的区间基本信度赋值(ibba)合成方法.将其称为CDI(Conflict Distribution of Interval-valued belief structure for combination)方法.
定义1 设Θ={θ0,θ1,…θn}为辨识框架,Xi(i=1,2,…,g)为辨识框架Θ上的焦元,区间值[ai,bi]⊆[0,1],则Θ上的区间基本信度赋值m(·)是有效的,须满足条件如下:
(1)ai≤m(Xi)≤bi;
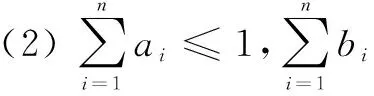

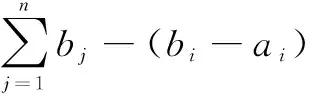
定义3 设Θ={θ0,θ1,…θn}为辨识框架,它的广义幂集G(G=2Θ或G=DΘ)下,存在n个独立的证据源β1,β2,…βn以及它们定义在G上的区间基本信度赋值m1(·),m2(·),…,mn(·),则区间信度质量矩阵为:

式中,g=|G|表示广义幂集G的维数.证据源βi给焦元Aj∈G分配的区间基本信度赋值对任意的1≤i≤n,1≤j≤g,有mij⊆[0,1].区间信度质量矩阵M描述了所有可用信息.



4.1 CDI1方法
当进行两个区间证据合成时,CDI1方法定义如下:




当进行多个区间证据合成时,CDI1方法定义如下:




4.2 CDI2方法
在CDI1方法中,冲突质量k在所有的非零焦元间进行分配;而在CDI2方法中,冲突质量k只在引起冲突的这部分焦元间按比例进行分配.
当进行两个区间证据合成时,CDI2方法定义如下:

max/min[(m1⊕m2)CDI2(X)]


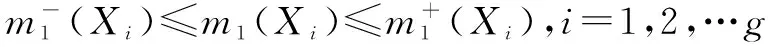

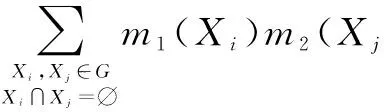
当进行多个区间证据合成时,CDI2方法定义如下:

max/min[(m1⊕m2⊕…⊕mn)CDI2(X)]

j=1,2,…g,对于∀i=1,2,…n.
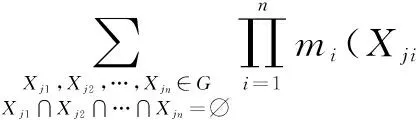
4.3 CDI3方法
在CDI1和CDI2方法中,都是直接对总冲突质量k在相关焦元中进行分配,而CDI3方法将构成k的各部分冲突质量分别在与之相关的焦元间进行重新分配.当模型中交集为空,m(A∩B)作为部分冲突质量只在非空焦元A和B之间,根据焦元A和B在区间信度矩阵M中所对应的列和的比例进行分配.此时,如果焦元A和B为空集或其所对应的列和为0,则质量m(A∩B)根据析取规则转移到非空集合u(A)∪u(B)上;如果u(A)∪u(B)也为空,则质量m(A∩B)转移到辨识框架Θ上.
当进行两个区间证据合成时,CDI3方法定义如下:

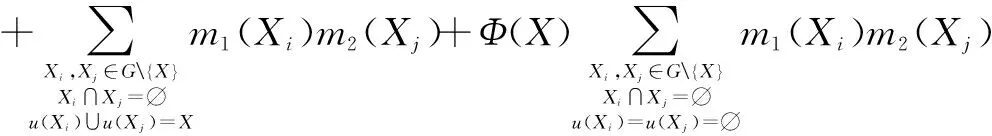

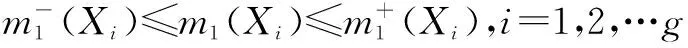

c12(X)+c12(Y)≠0,Y∈G{X},X∩Y=∅.
式中,c12(X)表示区间信度质量矩阵M中焦元X所对应的列和,即c12(X)=m1(X)+m2(X);Φ(X)是关于焦元X的特征函数,若X=θ1∪θ2∪…∪θn,则Φ(X)=1,否则Φ(X)=0.
当进行多个区间证据合成时,CDI3方法定义如下:

max/min[(m1⊕m2⊕…⊕mn)CDI3(X)]

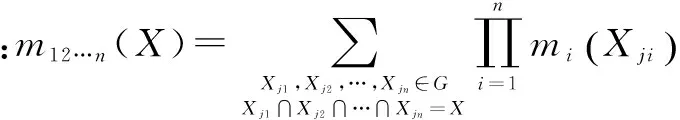
·m12…n(X∩Xj1∩…∩Xjk),

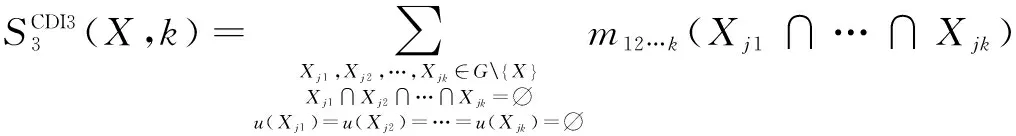



c12…n(X)表示区间信度质量矩阵M中焦元X所对应的列和,即c12…n(X)=m1(X)+m2(X)+…+mn(X);Φ(X)是关于焦元X的特征函数,若X=θ1∪θ2∪…∪θn,则Φ(X)=1,否则Φ(X)=0.
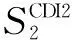
CDI4方法将之前CDI3方法分配所用的部分冲突质量进一步细分,以此获得更为精确的结果.例如,在辨识框架Θ={A,B}上,两条证据给出区间基本信度赋值m1和m2.与之前方法对冲突质量m(A∩B)进行重分配不同,CDI4方法对m(A∩B)又进一步细分为m1(A)m2(B)与m1(B)m2(A).其中,冲突质量m1(A)m2(B)将按m1(A)和m2(B)给出的比例在焦元A和B间进行分配,同样,冲突质量m1(B)m2(A)将按m1(B)和m2(A)给出的比例进行重分配.
两个区间证据合成时,CDI4方法定义如下:





多个区间证据合成时,CDI4方法定义如下:

max/min[(m1⊕m2⊕…⊕mn)CDI4(X)]=m12…n(X)

对于∀i=1,2,…n,
式中,{i1,i2,…in}∈Pn({1,2,…n}),Pk({1,2,…n})表示由{1,2,…n}中的k个元素所组成的集合.
5 算例分析
在本节中,将通过算例对CDI1~4方法的性质进行验证,并在Shafer模型下引入Wang方法;在混合DSm模型下引入区间DSm方法与CDI方法进行对比分析.
例1 在Shafer模型下,已知辨识框架为Θ={A,B,C},证据的区间基本信度赋值为:
m1(A)=[0.00,0.00],m1(B)=[0.96,1.00],
m1(C)=[0.02,0.04];
m2(A)=[0.96,1.00]-ε,m2(B)=[0.00,0.04]+ε,
m2(C)=[0.02,0.04].
在证据m2中,令ε=0,之后以0.01间隔步进至ε=0.96.此时两证据在焦元A,B上的赋值由完全冲突变为相一致.使用CDI各方法与Wang方法对证据进行组合,随着证据冲突变化,将涉及冲突的焦元A,B合成后的区间信度赋值变化趋势在图1,图2中给出.
图1中可以看出,当ε=0时,证据m1和m2完全冲突,CDI各方法给出m(A)的结果区间中位值都在0.5附近;随着ε的增加,证据m2为焦元A赋值逐渐接近于[0.00,0.04],CDI各方法所得结果都收敛到0.同时可以看出,Wang方法此时出现了“0-信任悖论”,即由于m1(A)=[0.00,0.00],所以得到的m(A)始终为0,无法得到正确的结果.在图2中,当ε=0,两证据完全冲突时,CDI各方法给出m(B)的区间中位同样在0.5附近;随m2(B)接近于区间[0.96,1.00],CDI各方法均收敛到1.但Wang方法得到的m(A)区间始终偏大.CDI方法在面对冲突证据时,得到较为合理的结果.
例2 在上例中,使两证据的区间信度赋值发生少量变化,以此对CDI各方法的鲁棒性进行验证.当ε=1×10-2,ε=1×10-4,ε=1×10-6,ε=1×10-8时,各方法所得的合成结果在表1中给出.
从表1中可以看出,随着证据区间变化幅度的减小,所得到的各焦元结果区间变化随之减小,并趋于稳定.CDI各方法具有较好的鲁棒性.在表1中,因CDI1,2方法得到的结果相同,故同时给出.
例3 在自由DSm模型下,已知辨识框架为Θ={A,B},证据的区间基本信度赋值为:
m1(A)=[0.50-η,0.50+η],m1(B)=[0.30,0.70];m2(A)=[0.70,0.90],m2(B)=[0.20,0.40].令η以0.01间隔从η=0步进至η=0.50,此时信度区间m1(A)由[0.50,0.50]增大至[0.00,1.00],以此对CDI方法与区间DSm方法在证据区间增大时所得结果的合理性进行验证.

表1 CDI各方法合成结果

方法变化量m(A)m(B)m(C)CDI1,2方法ε=1×10-2[0.460846,0.480053][0.489168,0.519351][0.019804,0.041152]ε=1×10-4[0.470305,0.489706][0.479332,0.509698][0.019998,0.041532]ε=1×10-6[0.470399,0.489803][0.479233,0.509601][0.020000,0.041536]ε=1×10-8[0.470400,0.489804][0.479232,0.509600][0.020000,0.041536]CDI3方法ε=1×10-2[0.469482,0.502140][0.493658,0.528580][0.001937,0.007508]ε=1×10-4[0.479134,0.512087][0.483722,0.518929][0.001937,0.007508]ε=1×10-6[0.479231,0.512187][0.483622,0.518832][0.001937,0.007508]ε=1×10-8[0.479232,0.512188][0.483621,0.518831][0.001937,0.007508]CDI4方法ε=1×10-2[0.476872,0.505276][0.491676,0.521704][0.001317,0.004991]ε=1×10-4[0.484284,0.512836][0.484431,0.514332][0.001186,0.004676]ε=1×10-6[0.484358,0.512911][0.484359,0.514258][0.001184,0.004672]ε=1×10-8[0.484359,0.512912][0.484359,0.514257][0.001184,0.004672]
在本例中CDI1~4方法仅使用合取规则进行计算,所得结果相同,故仅使用CDI1方法与区间DSm方法进行对比.同时,区间信度赋值函数在焦元B与A∪B上赋值的计算过程与m1(A)无关,仅将焦元A与A∩B的合成结果随m1(A)变化趋势在图3、图4中给出.
从图中可以看出,区间DSm方法合成的结果区间始终比CDI方法更为宽泛.且随着m1(A)区间增大,区间DSm方法得到的区间范围持续增加.
在图3中,当η=0,即m1(A)退化为单点值0.5时,区间DSm方法对m2(A)端点值与0.5做乘法运算,得到结果为[0.35,0.45];而实际情况是,由于m2(B)=[0.20,0.40],故m2(A)区间上界仅能取到0.8,CDI方法在添加约束条件m2(A)+m2(B)=1后,得到了更为合理的结果.同样,由于m1(A)+m1(B)=1的限制,m1(A)区间仅能从单点值0.5变化到[0.30,0.70],这也是m1(A)变化后期CDI合成结果保持恒定的原因.在图4中可以看出,随m1(A)区间上界接近于1,区间DSm合成结果在焦元A∩B上的赋值区间上界已为1,此时,区间DSm方法基本失效.
例4 两部雷达对同一目标的敌我属性进行识别的过程中,需要其分别给出判断,并通过合成得到最终结果.
首先构建辨识框架Θ={A,B},其中,A表示“我方目标”,B表示“敌方目标”,对于存在目标无法识别的情况,引入A∪B(“敌或我方目标”)表示.然后将雷达对该目标分属“敌方”、“我方”的支持程度作为区间基本信度赋值,在表2中给出.分别使用CDI1~4方法对证据进行合成.同时,由于本例中A∩B表示的“既是敌方又是我方目标”情况并不存在,可判断此例为Shafer模型,各方法合成结果在表3中给出.
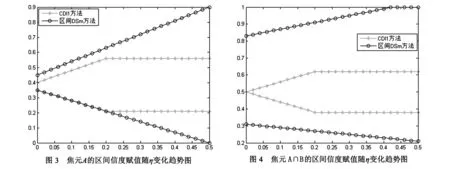
表2 基本区间信度赋值

证据ABA∪Bm1[0.334,0.467][0.361,0.402][0.268,0.392]m2[0.452,0.512][0.296,0.338][0.132,0.197]
在本例中,总的冲突质量为m(A∩B).CDI1方法将其部分分配到焦元A∪B上,导致该方法获得的效果较差.CDI2方法与CDI3方法得到了相同的结果,这是由于在CDI3方法中,唯一的冲突m(A∩B)仅在焦元A,B间分配一次,比例计算与CDI2方法相一致.同时,对于“敌我目标未知”的情况A∪B,由于其未涉及冲突,这4种CDI方法采用了相同的处理方式.与CDI方法相比,Denux方法由于优化步骤分开进行,得到的结果区间偏大,造成结果的精度降低,Wang方法对此进行了改进,得到结果与本文方法相差不大.
例5 在多传感器并发故障诊断应用中,由各传感器采集故障数据,再通过对其给出的结果进行信息融合,对系统故障状态进行判断.
假设辨识为Θ={A,B,C},表示三种单发故障,同时,系统内还可能存在故障A与故障C,故障B与故障C两种并发故障,即存在A∩C≠∅,B∩C≠∅.由于数据存在缺失,两传感器给出的各故障模式下的信度赋值为区间值,见表4.合成结果在表5中给出.

表4 基本区间信度赋值

表5 区间合成结果
本例中由于不存在故障A与故障B并发的情况,模型引入排斥性约束A∩B=∅,为混合DSm模型,总的冲突质量即为m(A∩B).由于CDI1方法将其分配到未涉及到冲突的焦元C上,导致该方法得到的结果存在偏差.CDI2,3方法得到的结果相同.但其与CDI4有略微不同,精确到万分位后有所体现.在对约束A∩B=∅的处理上,区间DSm组合规则直接将其质量m(A∩B)传递到了焦元A∪B上,作为未知信息进行处理.五种方法最终都得到了正确的诊断结果,即故障B与故障C并发.

表6给出了各方法的平均运算时间与融合精度.为便于比较,在使用区间DSm方法进行合成时,向模型中加入约束条件A∩B=∅.选用CDI4方法得到的结果区间作为基准,以其他各方法所得区间的上下边界平均偏差对融合精度进行度量.
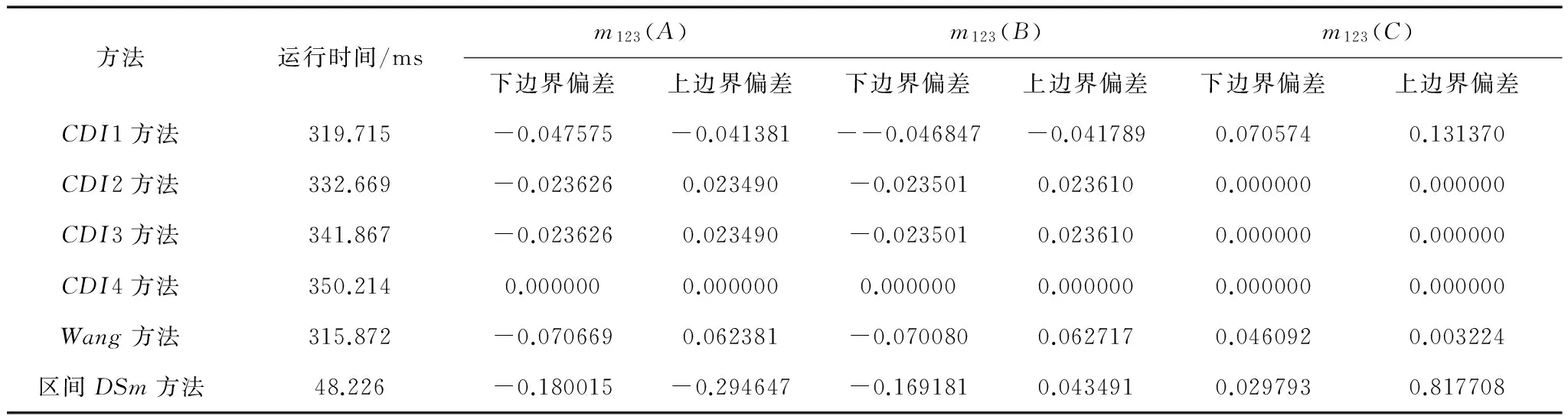
表6 各区间证据合成方法量化比较
CDI1~CDI4方法运算时间是递增的,但差别不大.但CDI方法运行于DSm模型下,产生最大可能焦元集的计算量要高于运行在Shafer模型下的Wang方法;同时,在进行焦元比对时,由于|Dθ|>|2θ|,也会造成计算量的增加.区间DSm方法用时最短,其只在区间两端点处分别各进行一次合成,无求解最优化问题过程.在对融合精度进行分析时,CDI1方法融合精度最低,CDI2、CDI3方法精度高于CDI1方法;Wang方法得到的在焦元A,B上的融合精度好于区间DSm方法,略差于CDI方法;区间DSm方法在三个焦元上所得的结果偏差都是最大的,融合精度最低.
对算法的时间复杂度进行分析,CDI方法的运算主要有三个步骤,即最大可能焦元集DΘ的产生、证据间焦元的比对与冲突分配、最优化问题求解.当辨识框架内元素个数为n时,产生DΘ的时间复杂度为:O1(f(n))=O(22n);第二步的时间复杂度与证据条数k及DΘ中元素个数相关,即O2(f(k,|Dθ|))=O(k!·|Dθ|k);而求解约束优化问题的时间复杂度与设定的迭代次数m相关,即O3(f(m))=O(m).由此可知,CDI各方法运算时间复杂度相同,为OCDI(f(n,k,|Dθ|,m))=O(max(22n,k!·|Dθ|k,m)).同时,Wang方法的时间复杂度OWang(f(n,k,|2θ|,m))=O(max(2n,k!·|2θ|k,m)),区间DSm方法的时间复杂度O区间DSm(f(n,k))=O(2k·2n).
在CDI1~CDI4方法的选择上,对运算时间不做要求的应用中,CDI4方法由于融合精度最高应优先选用.当焦元集中元素均与冲突有关时,CDI1与CDI2方法会得到相同的结果,此时应选用CDI1方法可降低运行时间;当焦元集中仅有两焦元冲突时,CDI2与CDI3方法得到结果相同,应选用CDI2方法,原因同上;否则,推荐使用CDI3方法,在运算时间与融合精度方面取得平衡.
6 结语
本文提出了CDI1~4共四种基于比例进行冲突分配的区间证据优化合成方法.它们可同时适用于DST框架与DSmT框架.有效地克服了目前区间信度组合方法面对高冲突证据失效的问题.通过算例验证,结果表明CDI方法得到的结果合理,有效,具有良好的收敛性.同时应注意到,目前针对精确信度结构合成过程中组合运算计算量过大问题的研究已展开[23,24],而CDI方法同样存在多焦元多证据条件下计算量大,合成困难的问题,有效地降低计算量将是未来的研究方向之一.
[1]Lee E S,Zhu Q.An interval dempster-shafer approach[J].Computers & Mathematics with Applications,1992,24(7):89-95.
[4]Smets P.Data fusion in the transferable belief model[A].Proceedings of the Third International Conference on Information Fusion[C].IEEE,2000.21-33.
[5]Wang Y M,Yang J B,Xu D L,et al.On the combination and normalization of interval-valued belief structures[J].Information Sciences,2007,177(5):1230-1247.
[6]陈圣群,王应明.区间值信念结构下冲突证据组合[J].系统工程理论与实践,2014,(1):256-261.
Chen Shengqun,Wang Yingmin.Conflicting evidence combination of interval-valued belief structures[J].Systems Engineering Theory&Practice,2014,(1):256-261.(in Chinese)
[7]康兵义,李娅,邓勇,等.基于区间数的基本概率指派生成方法及应用[J].电子学报,2012,40(6):1092-1096.
Kang Yibing,Li Ya,Deng Yong,et al.Determination of basic probability assignment based on interval numbers and its application[J].Acta Electronica Sinica,2012,40(6):1092-1096.(in Chinese)
[8]Smarandache F,Dezert J.An introduction to DSm theory of plausible,paradoxist,uncertain,and imprecise reasoning for information fusion[J].Octogon Mathematical Magazine,2007,15(2):681-722.
[9]Shafer G.A Mathematical Theory of Evidence[M].Princeton:Princeton University Press,1976.
[10]Dubois D,Prade H.A Set-Theoretic View of Belief Functions[M].Springer Berlin Heidelberg,2008.375-410.
[11]Smets P.Analyzing the combination of conflicting belief functions[J].Information Fusion,2007,8(4):387-412.
[12]Murphy C K.Combining belief functions when evidence conflicts[J].Decision support systems,2000,29(1):1-9.
[13]Smets P,Kennes R.The transferable belief model[J].Artificial Intelligence,1994,66(2):191-234.
[14]Yager R R.On the dempster-shafer framework and new combination rules[J].Information Sciences,1987,41(2):93-137.
[15]Dubois D,Prade H.Representation and combination of uncertainty with belief functions and possibility measures[J].Computational Intelligence,1988,4(3):244-264.
[16]Lefevre E,Colot O,Vannoorenberghe P.Belief function combination and conflict management[J].Information fusion,2002,3(2):149-162.
[17]Dezert J.Foundations for a new theory of plausible and paradoxical reasoning[J].Information and Security,2002,9:13-57.
[18]Smarandache F,Dezert J.Advances and Applications of DSmT for Information Fusion (Collected works)[M].American Research Press,2009.
[19]Dezert J,Smarandache F.Proportional conflict redistribution rules for information fusion[A].Advances and Applications of DSmT for Information Fusion (Collected works second volume)[C].Rehoboth,American Research Press,2006,3-66.
[20]Dambreville F,Celeste F,Dezert J,et al.Probabilistic PCR6 fusion rule[J].Advances and Applications of DSmT for Information Fusion,2009,3:137-160.
[21]Smarandache F,Deserts J.A simple proportional conflict redistribution rule[J].Multispace & Multistructure.Neutrosophic Transdisciplinarity (100 Collected Papers of Science),2010,4:304.
[22]Smarandache F,Dezert J.On the consistency of PCR6 with the averaging rule and its application to probability estimation[A].16th International Conference on Information Fusion[C].IEEE,2013,1119-1126.
[23]李新德,黄心汉,孟正大,等.一种快速分层递阶 DSmT 近似推理融合方法 (A)[J].电子学报,2010,38(11):2566-2572.
Li Xinde,Huang Xinhan,Meng Zhengda,et al.A fast approximate reasoning method in hierarchical DSmT(A)[J].Acta Electronica Sinica,2010,38(11):2566-2572.(in Chinese)
[24]李新德,杨伟东,吴雪建.一种快速分层递阶DSmT近似推理融合方法(B)[J].电子学报,2011,39(A3):31-36.
Li Xinde,Yang Weidong,Wu Xuejian,et al.A fast approximate reasoning method in hierarchical DSmT(B)[J].Acta Electronica Sinica,2011,39(A3):31-36.(in Chinese)

孙伟超 男,1986年生于山东烟台.海军航空工程学院电子信息工程系博士研究生.研究方向为复杂装备故障诊断.
E-mail:ben-phoenix@163.com
许爱强 男,1963年生于山东青岛.海军航空工程学院电子信息工程系教授.研究方向为军用电子装备故障诊断.
E-mail:xuaq6342@yahoo.com.cn
Approaches for Combination of Interval-Valued Belief Structures
SUN Wei-chao1,XU Ai-qiang2,LI Wen-hai2
(1.GraduateManagementUnit,NavalAeronauticalEngineeringInstitute,Yantai,Shandong264001,China; 2.AutomaticTestEquipmentLaboratory,NavalAeronauticalEngineeringInstitute,Yantai,Shandong264001,China)
In the process of data fusion with evidence theory,precise belief structures required in original evidence theory are not always available.At this point,approaches for combination of interval-valued belief structures is needed.Existing approaches in DST and DSmT framework are reviewed,examined and analyzed.The paper proposed four version of CDI (Distribution Conflict of Interval-valued belief structures) for combination of evidence.CDI1~CDI4 are all fit for DST and DSmT framework.The approaches can deal with imprecise and uncertain information.The accuracy of combination result from CDI1~4 improves gradually.Numerical examples and comparison of results of existing approaches for interval-valued belief structure are provided throughout the paper.
interval-valued belief structures;Dezert-Smarandache theory(DSmT);rules of evidence combination
2015-02-23;
2015-08-13;责任编辑:蓝红杰
总装预研基金(No.6140A27020212JB14311)
TP182
A
0372-2112 (2016)11-2726-09
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.11.023

