小变量情况下第一类整数阶Bessel函数的计算
冯佳计,贾晓伟,沈建琪
(上海理工大学理学院,上海200093)
小变量情况下第一类整数阶Bessel函数的计算
冯佳计,贾晓伟,沈建琪
(上海理工大学理学院,上海200093)
在计算第一类整数阶Bessel函数时,后向递推算法稳定高效.然而,起始点的选取必须有足够高的阶数,并且需要进行归一化处理.本文对Taylor级数展开算法进行研究,并对其级数展开规律、计算精度,以及求和项与参数间的关系进行了讨论.此外,本文利用指数形式,极大扩展了该算法的可计算范围.与du Toit算法、MATLAB和Mathematica应用软件的计算结果比较显示,本文的算法具有较高的准确性和稳定性.
Bessel函数;Taylor级数展开;指数扩展
1 引言
第一类整数阶Bessel函数Jn(z)在物理学、力学、电磁学、环境科学等领域都有着重要的用途[1,2].由于应用广泛,大量文献致力于讨论它的性质并给出了多种不同的算法[3~16].其中后向递推算法选取两个连续的高阶函数作为起始点赋任意值并后向递推计算,最后做归一化处理[9~11].这种算法稳定且高效.然而,为了确保计算的顺利进行,后向递推算法起始点的阶数必须足够高,需要更多的计算机资源和更大的计算量.在采用后向递推算法计算Bessel函数时,可考虑采用Taylor级数展开法精确计算出起始阶数的函数值以提高计算效率.原则上,Bessel函数的Taylor级数展开对所有变量均收敛.然而,其收敛速度却依赖于阶数n和变量z的大小.在阶数n很小、参数z很大的情况下,需要计算的级数展开项增多,且在计算过程中有可能会丢失有效数字,导致计算效率降低、计算结果出现偏差.
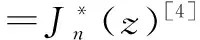
2 递推算法
整数阶Bessel函数满足前向递推关系
(1)
或者后向递推关系
(2)
对于给定参数z,前向递推从两个连续低阶级数开始计算,而后向递推从两个连续高阶级数开始计算.像大多数递推过程一样,上述公式易受传播误差的影响[7].
当z为实数或者虚部很小(|lmz|≤1.0)的复数时,Bessel函数的绝对值|Jn(z)|在n<0.9|z|范围变化不大,而在n≥0.9|z|范围随阶数的增大快速衰减.对于n<0.9|z|的范围,前向递推或者后向递推都能用来计算Jn(z);但当n>0.9|z|时,则只能采用后向递推法[5,9].如果z的虚部较大,Bessel函数的绝对值|Jn(z)|在n≥0范围内随阶数的增大迅速衰减,只能采用后向递推法计算.
用后向递推方法计算Bessel函数Jn(z)需从两个连续的高阶级数Bq(z)和Bq+1(z)开始,Bq(z)和Bq+1(z)的值可以任意选取,du.Toit建议Bq(z)=1和Bq+1(z)=0[9].然而,阶数q必须同时满足env|Jq+1(z)|≤10-p/2env|JN(z)|和env|2Jq(z)|≤10-penv|J0(z)|以确保收敛,其中p为所需的有效位数、N是所需计算的最高阶数,env|x|表示函数的包络线.如果N≤|z|,q的最小值需满足
(3)
若N>|z|,q值的选取则相对繁琐[5,11].完成Bn(z)的计算后,需进行归一化处理得到相应的函数值Jn(z).针对不同的变量值,采用不同的归一化方法.当|z|≤25时,Bn(z)归一化处理为
(4)
当|z|>25时,使用S=B0(z)/J0(z)或S=B1(z)/J1(z)归一化效率更高.使用时应避开J0(z)和J1(z)的零点.
从以上讨论可知,后向递推法从两个任意取值Bq(z)和Bq+1(z)开始计算,不仅需要计算起始阶数q以及从阶数q到阶数N的函数Bn(z),还需对Bn(z)做归一化处理.因此,为了使计算更加高效,在使用后向递推方法时,建议采用Taylor级数展开法预先计算Bq(z)和Bq+1(z)的精确值.
3 Bessel函数的Taylor级数展开
整数阶Bessel函数Jn(z)的Taylor级数展开式为:
(5)
令
(6)
(7)
则有递推关系:
(8)
(9)
(10)



对于复变量的一般情况z=|z|eiδz,Taylor级数展开形式写成如下形式:
(11)
(12)

(13)
(14)
公式(13)中的求和项在计算过程中出现正负交替的情况,如果kpeak比较大,必然导致数值比较大的数字相减并导致有效数字丢失从而计算结果变差.反之,公式(14)中的求和项一直为正,不会出现公式(13)的情况.因此,在这种情况下,即使kpeak比较大,也能得到合理的计算结果,但求和项比较多、收敛较慢.



(15)
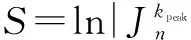
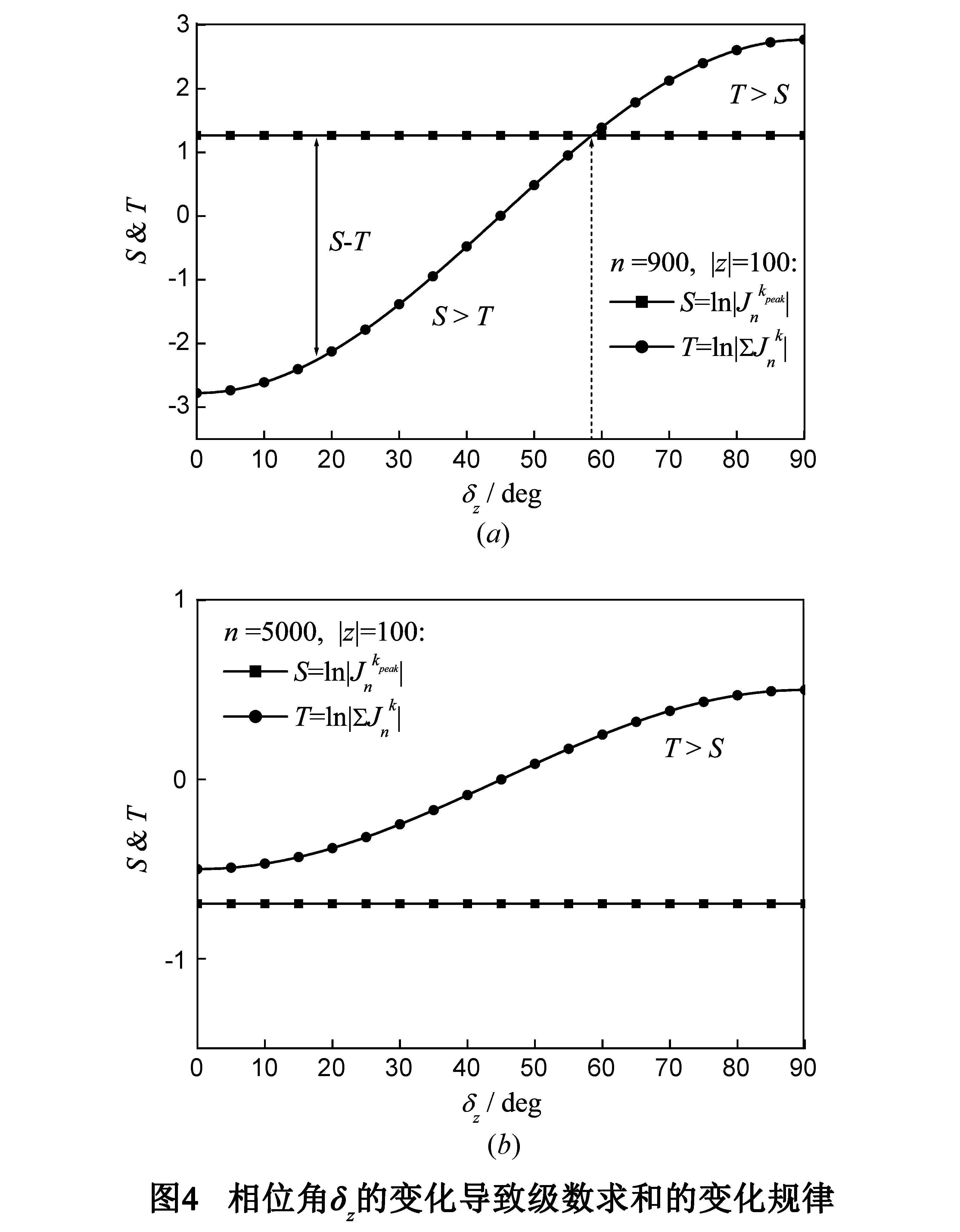

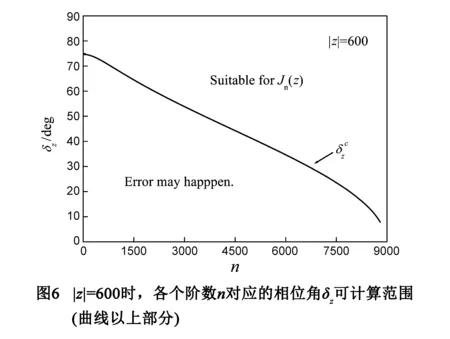
在采用Taylor级数展开式时,并不一定要求严格满足(|z|/2)2 相位角δz=0时有效数字丢失最严重,因此在该相位角情况下满足S-T<18的所有阶数ncal对所有的相位角计算均是可信的(见图5).可以看出,ncal≈|z|2/40-10表示满足n>ncal时,对于任意相位角δz的计算结果保证至少7位有效数,这与n>|z|2/4-1的要求降低了大约10倍. 图6给出了|z|=600时阶数n和相位角δz的关系,以曲线为界,上部区域表示Taylor级数展开式适用的范围,下部区域中计算得到的结果其有效位数低于7位.显然,如果提高对有效位数的要求,则图中的曲线将会向上移动,对应的可计算范围缩小. 在20<|z|<104范围内对多个不同的复变量z进行了数值计算,并进行曲线拟合,得到如下经验公式: (16) a=ln(|z|-0.5232|z|0.3+20.49)-2.997 (17) (18) 在复变量情况下,Bessel函数值及其Taylor级数展开式的求和项在一个很大的动态范围内变化.为了保证计算的顺利进行,需要对中间计算量的数值范围进行扩展.为此,所有变量均采用复数形式储存并参与运算. (19) 为了验证本文提出的算法,我们将所得结果与du 表1 Jn(z)数据比较 本文介绍了第一类整数阶Bessel函数的Taylor级数展开算法.为了保证高速收敛并且具有较高的计算精度,Taylor级数展开应在n≥|z|2/4-1条件下使用;在保证7位有效数计算精度的情况下,给出了Taylor级数展开式适用范围的经验公式;此外,在算法中采用了指数形式以扩展计算数值范围.计算结果与现有的软件进行了比较,表明该算法具有较好的效果. 递推算法与级数展开算法结合使用可有效提高计算效率.此外,本文中给出的算法也可以应用于计算非整数阶Bessel函数以及改进的Bessel函数. [1]G Gouesbet,G Gréhan.Generalized Lorenz-Mie Theories[M].Springer-Verlag Berlin Heidel-berg,2011. [2]JA Lock.Improved Gaussian beam-scattering algorithm[J].Applied Optics,1995,34 (3):599-570. [3]GN Watson.A Treatise on the Theory of Bessel Functions[M].Cambridge University Press,Cambridge,1958. [4]M Abramowitz,IA Stegun.Handbook of Mathematical Functions[M].10th ed.,National Bureau of Standards,Washington,DC,1972. [5]S Zhang,J Jin.Computation of Special Functions[M].Wiley,New York,1996. [6]M Goldstein,RM Thaler.Recurrence techniques for the calculation of Bessel functions[J].Mathematical Tables & Other Aids to Computation,1959,13(66):102-102. [7]W Gautschi.Computational aspects of three-term recurrence relations[J].Society for Industrial and Applied Mathematics,1967,9(1):24-28. [8]DE Amos.Algorithm 644:A portable package for Bessel functions of a complex argument and nonnegative order[J].Acm Transactions on Mathematical Software,1986,12:265-273. [9]CF du Toit.The numerical computation of Bessel functions of the first and second kind for integer orders and complex arguments[J],IEEE Antennas & Propagation Magazine,1990,38(9):1341-1349. [10]CF du Toit.Bessel functions Jn(z) and Yn(z) for integer order and complex argument[J].Computer Physics Communications,1993,78(1-2):181-189. [11]CF du Toit.Evaluation of some algorithms and programs for the computation of integer-order Bessel functions of the first and second kind with complex arguments[J].IEEE Antennas & Propagation Magazine,1993,35(3):19-25. [12]KG Valeev,OY Kostinskii.Calculation of Bessel functions by using continued fractions[J].Ukrainian Mathematical Journal,1997,47(12):1949-1950. [13]HA Yousif,R Melka.Bessel function of the first kind with complex argument[J].Computer Physics Communications,1997,106(3):199-206. [14]EJ Rothwell.Computation of the logarithm of Bessel functions of complex argument[J].Communications in Numerical Methods in Engineering,2005,21(10):597-605. [15]LW Cai.On the computation of spherical Bessel functions of complex arguments[J].Computer Physics Communications,2011,182(3):663-668. [16]张善杰,唐汉.任意实数阶复宗量第一类和第二类Bessel函数的精确计算[J].电子学报,1996,24(3):77-80. Zhang Shanjie,Tang Han.Accurate computation of Bessel functions of the first and second kinds with arbitrary real order and complex argument[J].Acta Electronica Sinica,1996,24(3):77-80.(in Chinese) 冯佳计 男,硕士研究生,1990年5月生于江西省抚州市东乡县.主要从事光学测试方面的研究. E-mail:jiaji19900505@163.com 沈建琪(通信作者) 男,1965年7月出生,浙江桐乡人,博士生导师,分别于1987年和1990年在华东师范大学获得理学学士和硕士学位,2003年在德国Cottbus工大获得工学博士学位.主要从事光散射颗粒测试技术研究. E-mail:jqshenk@163.com Computation of the Integer Order Bessel Functions of First Kind with Small Arguments FENG Jia-ji,JIA Xiao-wei,SHEN Jian-qi (CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China) Algorithm based on the backward recurrence for computing the integer order Bessel functions of the first kind is stable and efficient.However,the orders of the starting points should be high enough and the normalization is required.In this paper,we introduce an algorithm based on the Taylor series expansion (TSE),in which all the quantities involved are expressed in the exponential format so as to expand the numeric range of calculation.Comparison against du Toit’s algorithm as well as MATLAB and Mathematica shows that our algorithm is stable and reliable. Bessel function;Taylor series expansion;exponential scaling 2015-11-24; 2016-02-25;责任编辑:蓝红杰 国家自然科学基金(No.NSFC 51476104) TP301.6 A 0372-2112 (2016)11-2720-06 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.11.022



4 复数的大数计算方法
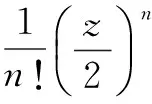
5 数值计算结果和分析


6 结论



