基于权值向量的偏好多目标优化方法
张兴义,蒋小三,张 磊
(1.安徽大学计算机与科学技术学院,安徽合肥 230039;2.安徽大学计算智能与信号处理教育部重点实验室,安徽合肥 230039)
基于权值向量的偏好多目标优化方法
张兴义1,2,蒋小三2,张 磊1,2
(1.安徽大学计算机与科学技术学院,安徽合肥 230039;2.安徽大学计算智能与信号处理教育部重点实验室,安徽合肥 230039)
偏好多目标优化方法是多目标优化领域的一个重要分支,其主要目的是仅搜索Pareto前沿面上部分区域内决策者感兴趣的解.基于MOEA/D算法根据预先设定的均匀分布的权值向量搜索Pareto最优前沿面的思想,本文提出了一种基于权值向量的偏好多目标优化方法,该方法通过引入具有偏好信息的权值向量,使算法仅搜索偏好点附近的解.仿真实验结果表明,与现有偏好多目标优化算法相比,本文方法具有支持多偏好点、偏好区域大小可控、偏好点位置无特别要求及偏好解具有更好收敛性的优势.
多目标优化;偏好多目标优化算法;权值向量;偏好解
1 引言
在工程实践中常常遇到需要同时优化多个目标的问题,这些目标之间往往相互冲突,因此没有唯一解能够同时使每个目标达到最好,而是具有各个目标之间相互妥协的一组Pareto最优解.通常称这类问题为多目标优化问题(MOP)[1~3].
当前国内外许多学者已提出了很多解决多目标优化问题的方法.如Deb等提出的NSGA-II[4],Zitzler等提出的SPEA2[5],Zhang等提出的MOEA/D[6],Zhang和Tian等人提出的KnEA[7]等算法在解决不同类型的多目标优化问题上有着各自不同的特点和优势.这些方法的最终目的是为了获得整个Pareto前沿面上均匀分布的一组最优解.然而,在实际的多目标优化应用问题中,决策者通常并不需要Pareto前沿面上所有区域上的最优解,而是只对其中部分区域上的解感兴趣.因此,决策者需要从多目标优化算法所得到的大量解中选取其偏好解,这对决策者来说具有一定的难度.另外,由于算法不是仅搜索决策者感兴趣的偏好解,因此在有限的时间内降低了其搜索偏好解的能力.针对此问题,研究人员提出了偏好多目标优化算法的思想,它在搜索过程结合决策者的偏好信息,使其仅搜索决策者感兴趣区域内的偏好解.
偏好多目标优化算法吸引了很多学者的研究,取得了大量的优秀成果[8~16].Wierzbicki首次提出了偏好多目标优化算法的思想,并基于这种思想建立了偏好多目标算法Achievement Scalarzing Functions(ASF)[8].ASF方法对于偏好点在Pareto前沿面上或前沿面外均可获得相应的偏好解.由于ASF方法采用把多目标问题转换为单目标问题的方式,因此每次仅能获得一个适合决策者偏好的解.为了获得更多的偏好解,Wierzbicki又提出了利用所得到的偏好解获得多个新偏好解的方法[8].2009年,Molina等提出了g-dominance方法[13],它通过偏好点定义了搜索的优先区域,是一种强化的Pareto支配关系,可以很容易的嵌入到多目标优化算法中.g-dominance方法的不足在于:(1)偏好点的位置对算法的影响很大,当将偏好点设置在Pareto面上或其附近时,甚至搜索不到Pareto最优解;(2)种群容易失去多样性,容易导致在一些局部最优较多的问题上收敛性较差.2010年Said等提出了r-dominance方法[14],该方法与g-dominance类似,是一种强化的Pareto支配关系,然而它比g-dominance具有更快的收敛速度,且偏好点的位置对算法的性能影响不大.2013年,邱飞岳等提出了双极支配的概念[15],该方法通过设置一个正偏好点和一个负偏好点,使偏好解尽量靠近正偏好点而远离负偏好点.2014年,郑金华等提出了如何利用角度信息引入决策者偏好[16].仿真实验表明它不仅支持多偏好点及偏好点位置(可行区域内,可行区域外或Pareto最优前沿面上)对实验结果影响不大,同时比r-dominance具有更好的收敛性.
本文在MOEA/D算法的基础上,提出了基于权值向量的偏好多目标优化方法,该方法通过引入具有偏好信息的权值向量,引导搜索向决策者感兴趣的区域进行,从而得到决策者感兴趣的偏好解.在一系列测试函数上的仿真实验表明,与已有偏好多目标优化算法相比,本文所提方法不仅具有支持多偏好点、偏好区域大小可控、偏好点的位置对算法性能影响不大等优点,同时,在大多数测试上所获得的偏好解具有更好的收敛性.
2 基于权值向量的偏好多目标优化算法
2.1 算法思想
本文所提出的基于权值向量的偏好多目标优化方法是受MOEA/D算法启发而建立的.MOEA/D算法是一种基于分解策略的多目标优化算法,它利用均匀分布的权值向量将一个多目标优化问题转化为多个单目标优化问题,其中每个权值向量对应一个单目标优化问题.MOEA/D算法根据预先设定的权值向量来搜索Pareto最优面,由于所设计的权值向量是均匀分布的,因此它可以搜索到分布在整个Pareto前沿面上的最优解.本文所提出的基于权值向量的偏好多目标优化方法的主要思想是把均匀分布的权值向量映射到偏好点附近,然后利用映射后的权值向量来搜索偏好点附近的Pareto最优解.
为此,对具有M个目标的多目标优化问题,定义如下映射:
(1)

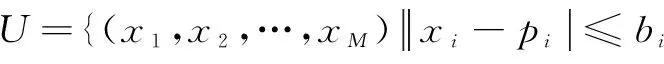
(2)
利用公式(1),可将均匀分布的权值向量映射到偏好点p的邻域U内.虽然公式(1)可以把权值向量映射到偏好点附近,然而按照这些权值向量进行搜索,所获得的Pareto最优解并不在偏好点附近.图1给出了偏好点为p=(0.5,0.2),邻域大小为b=(0.025,0.025)时,求解2目标DTLZ2问题所搜索到的偏好解.

为了解决映射后的权值向量与所搜到偏好解不对应的问题,首先分析该问题产生的原因.为使问题简单,下面仅考虑两个目标的情形.
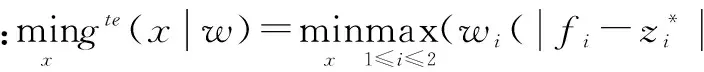
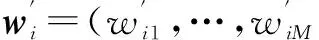
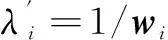
(3)
本文所提的基于权值向量的偏好多目标优化方法将使用公式(3)所示的权值向量进行搜索,下一节的仿真实验证明了这种方法是有效的.
另外,本文方法可以很容易扩展到多个偏好点的情形.设有k个偏好点p1,p2,…,pk,这时仅需要将所有的权值向量平均分为k组.为了使整个算法流程简单,本文对于种群个体的分配,也采用相同的方式,即把种群根据偏好点的数目平均划分为若干个子种群,每个子种群负责搜索一个偏好点附近的偏好解,在迭代过程中这些子种群的个体之间不进行任何交换,通过这种方式可以得到每个偏好点所对应的偏好解.本文所采用的支持多偏好点策略不同于文献[10],该文献中方法的主要思想是整个迭代过程中种群都是一个有机整体,在每次迭代过程中,优先选择离每个偏好点最近个体的邻域内的所有个体作为下一代种群的解.
2.2 算法描述
本文算法是在MOEA/D的基础上,引入了具有偏好信息的权值向量,建立的基于权值向量的偏好多目标方法,该方法的算法流程如算法1所示.算法1中的参数T,是用以控制邻居个体的数目.而参数δ为从邻居个体中选择个体的概率.本实验中设置T=20,δ=0.9.


3 仿真实验
3.1 参数的设置
为了验证本文方法的性能,下面与g-dominance[13]、r-dominance[14]和利用角度信息引入偏好[16]三种经典的偏好多目标优化算法进行了实验对比.本实验采用了4个ZDT问题7个DTLZ问题[17],即ZDT、ZDT2、ZDT3、ZDT4、DTLZ1、DTLZ2、DTLZ3、DTLZ4、DTLZ5、DTLZ6、DTLZ7.为了实验对比的公平性,本文中所有方法均采用模拟二进制交叉和多项式变异来产生后代,且实验中的模拟二进制交叉的分布指数设置为20,交叉概率为pc=0.9,多项式变异的分布指数也设置为20,变异概率为pm=1/n(n为决策变量的维数).实验中所有算法均使用相同大小的种群,在2、3、4、6、8、10目标的测试问题下种群大小分别设为100、105、120、132、156、275,且测试问题的决策变量维数设置ZDT1~ZDT3为30,ZDT4为10,DTLZ1~DTLZ6为M+9,DTLZ7为M+19,其中M为目标数目.算法的终止条件采用迭代次数,ZDT1~ZDT4问题的最大迭代次数设为300代,DTLZ1,DTLZ3问题的最大迭代次数设为1000代,DTLZ2~DTLZ7问题的最大迭代次数均设为500代,且以下所有统计结果均是独立运行30次的平均值.另外,所有对比算法中的非支配排序均采用了ENS算法[18].
3.2 实验对比
本文所提的基于权值向量的偏好多目标优化方法具有支持多偏好点、偏好区域大小可控的优势,同时比传统方法在大多数低维和高维多目标优化问题上可以获得具有更好收敛性的偏好解.下面分别对其进行实验验证.
3.2.1 支持多偏好点及偏好区域可控
由于高维问题不易可视化,以下实验仅展示本文算法在二维和三维问题上支持多偏好点和偏好区域可控性.对于高维多目标优化问题,本文方法仍具有支持多偏好点和偏好区域大小可控的特点.
首先验证本文方法支持多偏好点.图3给出了在同时设置(0,0.4)、(0.2,0.9)、(0.6,0.8)、(0.9,0.6)、(0.9,0)五个偏好点时,本文方法求解2目标DTLZ2问题搜到的偏好解.从图3可以看出,本文方法对于五个偏好点均能很好地搜到相应的偏好解,同时偏好点的位置(可行域内、可行域外、坐标轴上或Pareto面上)对搜索结果无影响.这说明本文方法支持多偏好点以及偏好点的位置对算法性能影响不大.

其次验证本文方法所搜索的偏好解的区域大小具有可控性.图4给出本文方法在分别设置不同的邻域大小下求解3目标的DTLZ1问题搜索到偏好解.从图4可以看出,本文方法搜索到偏好区域大小是可控的,b值越大,搜索到的偏好区域越大.决策者可以根据自己的需要,调节b中各元素的值,来控制偏好区域的大小.
3.2.2 低维上的收敛性对比实验
为了验证本文方法所搜索偏好解的收敛性,本文采用收敛性指标CM[19]值衡量,CM值越小表示算法的收敛性越好.实验对比中利用角度信息引入偏好的方法用以控制偏好区域大小的角度设为10°.r-dominance方法用以控制偏好区域大小的参数设为δ=0.35,本文方法用以控制偏好区域大小的参数设为b=0.01.*ones(1,M)(M为目标个数).

表1给出了四种方法在ZDT1~ZDT4问题和DTLZ1~DTLZ7低维问题上的CM值,从表1可以看出在ZDT1~ZDT4问题和DTLZ1~DTLZ7低维问题上,本文方法在所有方法中的收敛性是最好的.
为了验证本文方法的偏好效果,将其与g-dominance、r-dominance和利用角度信息引入偏好三种方法进行了实验对比.由于篇幅问题,以下仅给出在3目标DTLZ7问题上的偏好效果.
图5给出了四种方法在3目标DTLZ7问题上搜索到的偏好解.从图5可以看出,本文方法在DTLZ7测试问题偏好效果明显好于其他方法.

3.2.3 在高维上的收敛性对比实验
为了验证本文方法在高维问题上所搜索的偏好解的收敛性和偏好效果,测试了4种方法在4、6、8、10目标的DTLZ1~DTLZ7问题上的CM值,并图形展示了在10维DTLZ2问题上解的偏好效果.
表2给出了四种方法在DTLZ1~DTLZ7高维问题上的CM值,从表2可以看出,在DTLZ1~DTLZ7的高维问题上,本文方法在高维上有很好的收敛性.
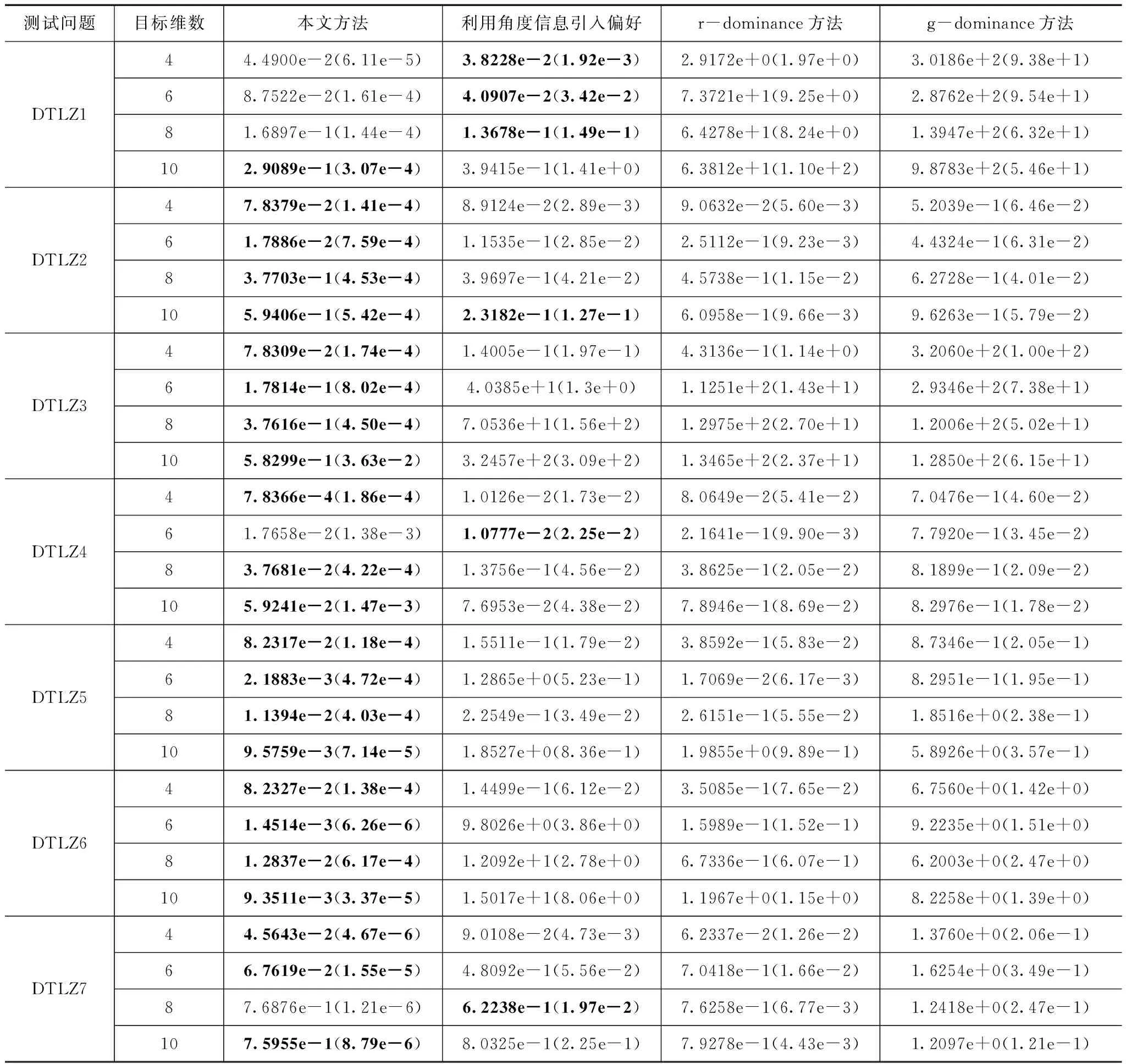
表2 四种方法在DTLZ1~DTLZ7高维问题上的CM值
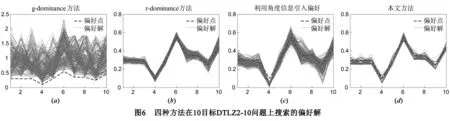
图6给出了四种方法在10目标的DTLZ2问题上搜索到的偏好解.从图6可以看出本文方法在高维问题上也有很好的偏好效果.
4 总结
本文受MOEA/D算法利用预先设定的均匀分布的权值向量来搜索Pareto最优解启发,提出了利用具有偏好信息的权值向量搜索偏好解的思想,并建立了基于权值向量的偏好多目标优化方法.与现有偏好多目标方法相比,仿真实验表明本文所提方法具有支持多偏好点、偏好区域大小可控、偏好点位置无特别要求及偏好解具有更好收敛性的优势.本文仅在标准测试函数上验证了算法的性能,然而,实际的工程应用中经常涉及到许多偏好多目标问题的优化,因此,下一步的研究重点,是在实际的工程应用问题中验证本文方法的有效性.
[1]崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社,2006.17-25.
[2]Zhou A M,Qu B Y,Li H,et al.Multiobjective evolutionary algorithms:a survey of the state of the art[J].Swarm and Evolutionary Computation,2011,1(1):32-49.
[3]Rachmawati L,Srinivasan D.Preference incorporation in multiobjective evolutionary algorithms:a survey[A].Proceedings of the Congress on Evolutionary Computation[C].Canada:IEEE,2007.962-968.
[4]Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[5]Zitzler E,Laumanns M,Thiele L.SPEA2:Improving the Strength Pareto Evolutionary Algorithm[M].Berlin:Springer,2002.95-100.
[6]Zhang Q F,Li H.MOEA/D:A multiobjective evolutionary algorithm based on decomposition[J].IEEE Transactions on Evolutionary Computation,2007,11(6):712-731.
[7]Zhang X Y,Tian Y,Jin Y C.A knee point driven evolutionary algorithm for many-objective optimization[J].IEEE Transactions on Evolutionary Computation,2014,dol.10.1109/TEVC.2014.2378512.
[8]Wierzbicki A P.The Use of Reference Objectives in Multiobjective Optimization[M].Berlin:Springer,1980.468-486.
[10]Deb K,Sundar J,Udaya Bhaskara R N,et al.Reference point based multi-objective optimization using evolutionary algorithms[J].International Journal of Computational Intelligence Research,2006,2(3):273-286.
[11]巩敦卫,王更星,孙晓燕.高维多目标优化问题融入决策者偏好的集合进化优化方法[J].电子学报,2013 42(5):933-939.
Gong Dunwei,Wang Gengxin,Sun Xiaoyan.Set-based evolution optimization algorithms integrating decision-maker’s preferences for many-objective optimization problems[J].Acta Electronica Sinica,2013,42(5):933-939.(in Chinese)
[12]Deb K,Kumar A.Light beam search based multi-objective optimization using evolutionary algorithms[A].Proceedings of the Congress on Evolutionary Computation[C].Singapore:IEEE,2007.2125-2132.
[13]Molina J,Santana L V,Hernández-Díaz A G,et al.g-dominance:reference point based dominance for multiobjective metaheuristics[J].European Journal of Operational Research,2009,197(2):685-692.
[14]Ben Said L,Bechikh S,Ghédira K.The r-dominance:a new dominance relation for interactive evolutionary multicriteria decision making[J].IEEE Transactions on Evolutionary Computation,2010,14(5):801-818.
[15]邱飞岳,吴裕市,邱启仓,王丽萍.基于双极偏好占优的高维目标进化算法[J].软件学报,2013,24(3):476-489.
Qiao Feiyue,Wu Yushi,Qiu Qicang,Wang Liping.Many-objective evolution algorithm based on bipolar preferences dominance[J].Journal of Software,2013,24(3):476-489.(in Chinese)
[16]郑金华,谢谆志.关于如何用角度信息引入决策者偏好的研究[J].电子学报,2014,42(11):2239-2246.
Zheng Jinhua,Xie Zhunzhi.A study on how to use angle information to induce decision maker’s preference[J].Acta Electronica Sinica,2014,42(11):2239-2246.(in Chinese)
[17]Huband S,Hingston P,Barone L,et al.Review of multi-objective test problems and a scalable test problem toolkit[J].IEEE Transactions on Evolutionary Computation,2006,10(55):477-506.
[18]Zhang X Y,Tian Y,Cheng R,et al.An efficient approach to non-dominated sorting for evolutionary multi-objective optimization[J].IEEE Transactions on Evolutionary Computation,2015,19(2):201-213.
[19]Deb K,Jain S.Running performance metrics for evolutionary multi-objective optimization[A].Proceedings of the Fourth Asia-Pacific Conference on simulated Evolution and Learning[C].Singapore:IEEE,2003,13-20.

张兴义 男,1982年生,2009年毕业于华中科技大学自动化学院,获得博士学位,现为安徽大学计算机科学与技术学院副教授、博士生导师.主要研究方向包括非传统计算模型与算法、多目标优化算法及应用、膜计算.
E-mail:xyzhanghust@gmail.com

蒋小三 男,1988年出生,安徽安庆人,现为安徽大学计算机应用技术专业硕士研究生.研究方向为偏好多目标进化算法.
E-mail:westsxj88@126.com

张 磊(通信作者) 男,1986年生于安徽安庆,2014年博士毕业于中国科学技术大学,现为安徽大学计算机学院讲师.主要研究方向为生物启发计算、约束模式挖掘、推荐系统.
E-mail:zl@ahu.edu.cn
A Weight Vector Based Multi-objective Optimization Algorithm with Preference
ZHANG Xing-yi1,2,JIANG Xiao-san2,ZHANG Lei1,2
(1.SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei,Anhui230039,China; 2.KeyLabofIntelligentComputingandSignalProcessingofMinistryofEducation,AnhuiUniversity,Hefei,Anhui230039,China)
Multi-objective optimization algorithms with preference are an important branch of multi-objective optimization.Its main aim is to find the Pareto optimal solutions in local regions interested by Decision Makers.Based on the idea of MOEA/D algorithm to search the Pareto front according to uniformly distributed weight vector,this paper proposes a weight vector based multi-objective optimization algorithm with preference.In the proposed method,the weight vector with preference is designed,by which the solutions around the preferred point interested by Decision Maker are found.Compared with existing algorithms,the simulation results verify that the proposed method can support multiple reference points,flexibly control the extent of preferred region,have no special requirement of the position of preference points and achieve better converge.
multi-objective optimization;multi-objective optimization algorithms with preference;weight vector;preferred solution
,Deb K.Integrating User P
into Evolutionary Multi-Objective Optimization[M].Berlin:Springer,2005.461-477.
2015-05-11;
2015-08-24;责任编辑:蓝红杰
国家自然科学基金(No.61272152,No.61502001);安徽大学学校学术与技术带头人引进工程(No.J10117700050)
TP18
A
0372-2112 (2016)11-2639-07
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.11.011

