600 m跨钢筋混凝土拱桥静风失稳全过程分析
谢长洲
(广西交通科学研究院,广西 南宁 530007)
600 m跨钢筋混凝土拱桥静风失稳全过程分析
谢长洲
(广西交通科学研究院,广西 南宁 530007)
文章根据桥梁静风稳定理论,针对600 m钢筋混凝土拱桥静风稳定性能问题,运用大型通用有限元软件ANSYS建立计算模型,分析拱桥随风速增加的静风失稳全过程情况,探讨拱桥在静风荷载下的失稳机理。
特大跨度;混凝土拱桥;静风稳定;ANSYS
0 引言
混凝土拱桥受到施工技术的限制,最大跨度一直徘徊在400多米。近些年来,日本、欧洲以及中国,相继开展了600 m级特大跨钢筋混凝土拱桥的试设计研究,以期这一传统桥型能够得到进一步发展。
1 600 m钢筋混凝土拱桥试设计概述
在我国,也有一些学者在开展特大跨度拱桥的研究,比如福州大学的陈宝春教授,收集了很多国外大跨径拱桥的实例[1];还有重庆交通大学的周水兴教授,针对600 m钢筋混凝土拱桥开展了大量的研究,并且提出了一个试设计方案,总体布置如图1所示,现将该试设计介绍如下[2]。
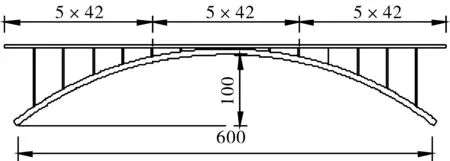
图1 600 m钢筋混凝土拱桥总体布置图
试设计方案是上承式拱桥,主拱跨径600 m,矢高100 m,矢跨比是1/6,拱轴线为悬链线。主拱圈拱顶拱脚截面试设计如图2所示。

图2 拱脚拱顶界面尺寸示意图
2 桥梁结构的有限元模型
充分利用ANSYS独特的求解器和方便的APDL程序语言,建立试设计桥梁的全桥模型和结构优化程序。
基本模型的内容主要包括:材料参数的设定、单元的离散、约束和荷载的施加。
为体现分析重点,节约计算时间。采用计算精度高的beam188梁单元模拟主要承重结构拱圈,拱圈一共划分为600个单元,沿水平向每米划分单元。采用计算精度相对低但能够达到要求的梁单元beam188模拟次要结构立柱和桥面梁。在划分单元时,有限元模型如图3所示。
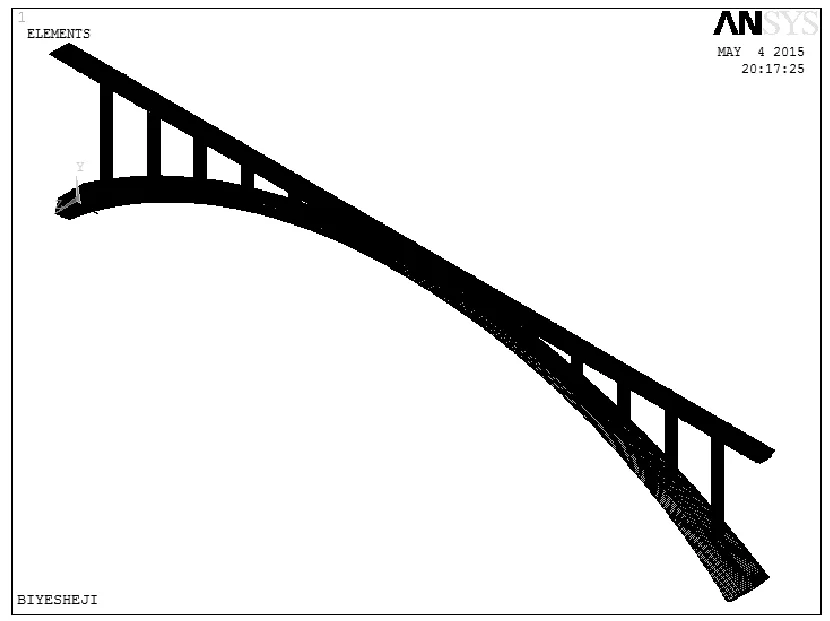
图3 ANSYS有限元模型图
试设计桥梁的约束是将拱脚处所有节点的6个方向的自由度进行约束,主拱圈与立柱采用节点耦合方式模拟刚接,前4根立柱与主梁采用刚接,后面采用铰接。
模型中拱圈采用C80混凝土材料,拱上立柱和桥面梁采用C40混凝土材料。具体材料参数见表1。

表1 材料特性表
C40混凝土的应力应变曲线如图4所示。
<1),且各件产品是否为不合格品相互独立.

图4 C40混凝土应力应变曲线图
C80混凝土的应力应变曲线如图5所示。

图5 C80混凝土应力应变曲线图
3 静风荷载加载全过程分析
研究非线性静风稳定性,采用增量与内外两重迭代方法[3][4]。按照上一节中建立的计算模型,对600 m钢筋混凝土拱桥模型逐级施加风荷载直至静风失稳。设定初始风攻角为0°,风速由0 m/s逐步增加,直至增加到模型失稳的风速。计算模型在每个风速下的响应,提取每个风速下模型的位移和应力,用来进行桥梁静风失稳全过程分析。
3.1 主拱圈变形随风速变化的全过程
在0°初始风攻角的工况下,提取每级风速下主拱拱顶处竖向、横向及扭转角变形值,其全过程变化如图6~8所示。

图6 主拱圈拱顶竖向位移随风速变化曲线图

图7 主拱圈拱顶处横向位移随风速变化曲线图

图8 主拱圈拱顶处转角随风速变化曲线图
计算结果表明,当风速<90 m/s时,拱顶处的变形随着风速的增大趋近于呈线性态势递增;当风速>90 m/s后,随着风速的增大,拱顶处的变形陡然增大。当风速达到109 m/s时,结构的变形已不再收敛,说明结构已经达到静风失稳的状态。
在主拱圈随风速的变化过程中,主拱圈的侧向位移增加很大,竖向位移有所增加;转角位移在风速90 m/s之前都只有略微增加,风速90 m/s之后,转角位移增加得非常快,转角位移增加斜率基本趋于竖直线。虽然直到临界风速109 m/s的时候,模型的转角都不大,但是,扭转刚度基本已经失效。
3.2 应力随风速变化的全过程
当风速从10 m/s逐渐增大到109 m/s,主拱拱顶截面的应力随风速变化全过程情况见图9。

图9 拱顶截面下缘应力变化曲线图
从图中数据可以看出,当风速<60 m/s的时候,随着风速的增加,拱顶截面下缘处的应力,呈逐渐变大的趋势;当风速>60 m/s,<100 m/s时,拱顶下缘的应力由大变小,在风速达到10 m/s后,随着风速的增加,拱顶下缘的应力迅速地减小。
从拱顶应力全过程变化中可知:主拱在受到风荷载后,有竖向变形和横向变形,变形引起主拱轴力和竖向弯矩的增加,在风速减小的时候,竖向弯矩增加得慢,此时,增加的轴力占主要作用,所以表现出来是应力增大;当风速逐渐增大,拱桥的竖向位移增加得越来越快,竖向弯矩也就显著地增加,此时,轴力的增加速度没有竖向弯矩增加得快,所以,拱顶下缘的应力就变为逐渐地减小。
当风速从10 m/s逐渐增大到109 m/s,拱顶截面的侧向应力随风速变化的全过程如下页图10所示。
从图10中可以看出,拱顶截面侧向应力是逐渐增加的,图中的变化趋势也基本上与拱顶的侧向位移全过程(见图7)相吻合。

图10 拱顶截面背风侧应力图
3.3 静风失稳风速时结构分析
桥梁结构在临界风速109 m/s时,结构的变形如图11~13所示。
从变形图中可以看出,结构竖向变形最大出现在跨中位置;而横向变形最大出现主梁的钢构段和连续梁段相交的位置,该位置是钢构的边跨和连续梁的边跨支撑的位置,结构的约束较小,横向变形最大。

图11 风速109 m/s时变形立面图(放大20倍)

图12 风速109 m/s时变形平面图(放大20倍)

图13 风速109 m/s时变形侧面图(放大20倍)
桥梁结构在临界风速109 m/s时,主拱圈的应力如图14~15所示。
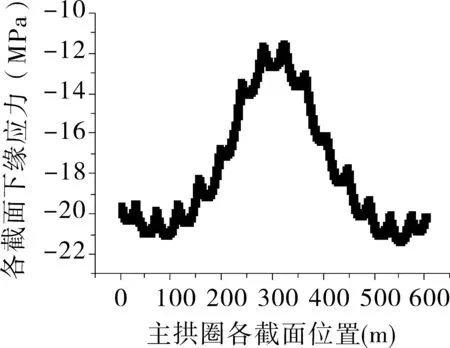
图14 主拱圈各截面下缘应力图
主拱圈在竖直方向受自重作用和风的竖向分力的共同作用,各个截面的下边缘受到轴力产生的压应力和竖向弯矩产生的正应力,从图中可以看出拱圈各截面下缘应力,都是压应力,且 图15 主拱圈各截面背风侧应力图 主拱圈在水平方向受风的水平分力的共同作用,各个截面的左右侧应力来自轴力产生的压应力和横向弯矩产生的正应力,从图中可以看出拱圈各截面背风侧应力,最小应力在拱脚附近,且>C80的抗压强度,所以在临界风速下,拱脚已经进入了塑性阶段。 根据本文关于全过程空气静力稳定的统计分析,可以将静风失稳的过程描述为:拱桥在静风荷载作用下,结构发生变形,结构的转角位移会使得静风荷载的有效风攻角变大,从而引起三分力系数的改变,进而引起静风荷载的非线性变化。在初期风荷载比较小时,静风荷载基本呈线性的增长,拱桥的变形较小,刚度不变,所以拱桥结构的变形随风速的加大基本处于近似直线的非线性增加;当风速>90m/s之后,拱桥结构的刚度减小,结构变形增加得很快,其中,扭转变形增加得最快,扭转变形的增加,又引起静风荷载的迅速增加,从而形成拱桥刚度变小,扭转变形增大,静风荷载加大,拱桥刚度进一步变小的循环中。当风速达到110m/s时,拱脚处的应力已经达到C80混凝土的极限应力,因此,结构变形不能收敛,说明拱桥结构出现静风失稳。 [1]陈宝春,黄卿维.600m跨径混凝土拱桥的试设计研究[J].中外公路,2006(1):80-82. [2]陈波旭.600m级跨钢筋混凝土拱桥主拱截面研究[D].重庆:重庆交通大学,2013. [3]陈政清.桥梁风工程[M].北京:人民交通出版社,2005. [4]程 进,江见鲸,肖汝诚,等.考虑几何与材料及静风荷载的非线性因素的大跨径桥梁静风稳定分析法[J].应用力学学报,2002(4):117-121,167. Static Wind Instability Full-process Analysis of 600m-span Reinforced Con-crete Arch Bridge XIE Chang-zhou (Guangxi Transportation Research Institute,Nanning,Guangxi,530007) According to bridge static-wind stability theory,and regarding the static wind stability problem of 600m reinforced concrete arch bridge,this article established the calculation model by using the large general-purpose finite element software ANSYS,analyzed the whole static wind instability process of arch bridge increasing with wind speed,and discussed the instability mechanism of arch bridges under static wind load. Super-large span;Concrete arch bridge;Static wind stability;ANSYS U448.22 A 10.13282/j.cnki.wccst.2016.09.019 1673-4874(2016)09-0071-04 2016-05-14 谢长洲(1989—),硕士,研究方向:公路桥梁设计。
4 结语

