浅谈初中数学教学中如何创设问题情境

张明媚

（播州区团溪镇中学 贵州遵义 563131）

浅谈初中数学教学中如何创设问题情境

张明媚

（播州区团溪镇中学 贵州遵义 563131）

在数学教学中，培养学生的思维能力需要创设问题情境，即利用和现实生活中的现象类比的方法创设问题情境；对老问题进行延伸创设问题情境；利用数学建模的方法创设问题情境；利用联想来创设问题情境；利用简单的数学实验来创设问题情境；利用数学材料创设问题情境；利用数学故事、典故来创设问题情境。

数学教学 问题情境 方法

近年来，我们在各级领导的组织指导下，进行数学教学中创设问题情境的方法的探索，通过互听探索公开课，听后进行讲座和总结的方法来研究。通过教学实践的探索、检验探索的效果，最后总结出以下方法：

一、利用和现实生活中的现象类比的方法创设问题情境

学生的绝大部分时间都在生活，认识最牢靠和最根深蒂固的部分就是生活中经常接触和经常用的知识。有些已经进入他们的潜意识，如果教学中能运用这些知识做类比，那么将是非常受学生欢迎的，一旦接受也会被学生牢牢的掌握，而现代的教学手段很容易让现实生活中的现象再现或模拟于课堂之上。

例如：在整式同类项的教学中，我们可以和实际中的例子相比较，把数学分类的思想形象化，在电化教室对一群猪羊的图片进行分类，分类的方法：无角的是猪，有角的是羊。这基本就是一个游戏，每个同学都可以轻而易举的做到，对于七年级的同学，还感到新奇以至于达到情绪高涨，这时抓住时机自然的过渡到同类项的分类中来，分类的方法：字母相同，相同字母的指数相同；学生乘胜追击，很自然的应用刚刚在猪羊分类中形成的程序，先看字母，再看字母的指数。

即：猪羊的分类（按外部形态） 多项式的分类（按字母和字母的指数）

在初二根式的加减运算中也可以做这样的比喻，实际上他们和合并同类项是一样的，这样不仅降低了问题的难度并且加深了学生对问题的理解，同时让学生接触了数学分类的思想。

二、对老问题进行延伸创设问题情境

解决问题和一个人的知识水平、认知结构等有关。作为教师如果能贴切的了解 学生的知识水平、认知结构，并适当的发展他，不仅能够完成教学任务，而且能够深化这种结构，使学生如何学习，并且大胆的发现问题、提出问题。例如：在七年级的几何开始部分有这样一道题：

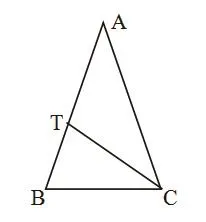
在等腰三角形ABC中，∠A=30º，又CT平分∠ACB，求ATC的度数。

这是一道基本考察了学生等腰三角形、角平分线以及三角形内角和的概念，如果仅仅让学生解决这道问题。教学就有些平淡了，如果在解决了这道问题之后，再向深处挖掘，进一步深化学生认知结构，将是非常有益的；我进一步提出了如下的问题：对于∠A=x度，你能用含x的代数式表示∠ATC吗？这看上去是一小步，仅仅是把30度换成了x0，数字换成了字母，实际上却是一大步，它巩固了前面的多项式，也和函数有了联系。当问题解决了，我再紧追一问：当x等于多少时，∠ATC=50º？这就成了一个方程问题，这就充分利用了前面的问题情境。不仅巩固知识，也发展了知识，对于学生发问，思考都是有利的。

要把学生从题海中解放出来，就需要我们老师精选习题 ，要题尽其用，通过习题最大的锻炼学生的思维能力和对知识的把握能力。

三、利用联想来创设问题情境

在初中数学教学中，一题多解、多题一解的现象是很普遍的。让学生较多的接触，适当的总结，是有利于学生发散思维能力的提高。匈牙利数学教育家、乔治·波利亚在《怎样解题》中指出：“要联想有没有做过类似的题目，有没有做过条件相似的题目。有没有做过结论相似的题目。”例如：在作好了这样一道题目后：线段AB中点为D，若线段BD的长度为5cm，那么线段AB的长度是多少？我再给学生提出这样的问题：已知∠AOB的角平分线为OC，∠AOC的角平分线为OD，若∠COD的度数为500，那么∠AOB的度数是多少？这两道题目的考察角度不同，但方法完全一样，对于低年级的同学学习几何问题是很好的。利用联想来创设情境的关键是要找出问题相似的地方，及“形似”（条件或结论一样），“神似”（方法或解题的思路一样）。“形似”我们称之为一题多变，而“神似”我们称之多题一解。

五、利用简单的数学实验来创设问题情境

利用数学实验的方法来创设问题的情境在低年级的实验几何阶段是很平常的事情，先让学生观察实验，然后总结得到数学结论，如求圆柱的体积，采用了把圆柱进行分割，拼成一个近似的长方体，分得越多，越接近一个长方体，让学生观察两者之间的关系，从而得到长方体的体积公式。在初中的高年级，数学实验几乎为零，但我们可以通过数学软件来模拟实验的过程，例如讲解勾股定理时，让学生通过观察不同的直角三角形三边平方的关系来得到勾股定理：如图所示。

三个正方形面积分别代表了三边的平方。定义一个小正方体面积为1个面积单位，通过查正方体的个数就可以得到三边平方的关系了。

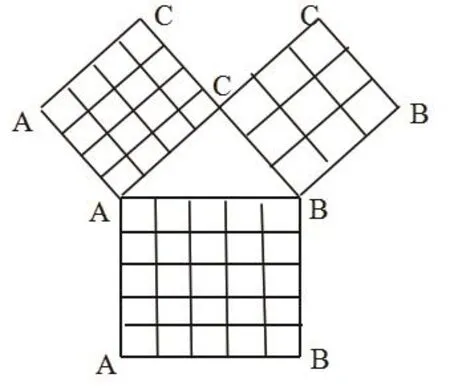
《几何画板》可以演示较多的数学实验特别是几何中数量关系。

六、利用数学材料创设问题情境

数学中，通过观察材料，观察方法，观察思路来启发学生思考得到新的结论，这类方法更适合开放型题目的设置，更容易让学生发挥发散性思维。

可以观察到，被减数与减数的分子都是1，分母是相邻的两个正整数时，差的分母是两个相邻自然数的积。

学生的视角不同，得到的结论既不同。针对上面的问题，在老师的启发下，学生互相启发，也就得到了更多的结论。如：（n为正整数），学生通过观察归纳：两个加数的分子为1，分母是相邻的两个正整数时，和的分母是这两个正整数的积，分子是较小整数的2倍加1。

七、利用数学故事，数学典故来创设问题情境

数学故事、 数学典故有时反映了知识形成的过程，有时反映了知识点的本质，用这样的故事来创设情境不仅能够加深学生对知识的理解，还能加深学生对数学的兴趣，提高数学的审美能力。例如：在讲解平面直角坐标系的过程中，我们可以先见解数学家欧拉发明坐标系的过程，躺在床上静静地思考如何确定事物的位置，这时发现苍蝇粘在了蜘蛛网上，蜘蛛迅速地爬过去把它捉住。欧拉恍然大悟：“啊，可以像蜘蛛一样用网格来确定事物的位置啊。”引入正题，怎样用网格来表示位置。这时学生的兴致已经调动起来了。

综上所述，数学教学是一个系统工程，培养学生的能力是最终目的，而创设问题情境只是一个手段，创设问题情境的方法也决不仅仅这几种，他需要我们不断的探索和自身知识的不断丰富，需要我们对生活的热爱和对教育的热情。