殊途同归，巧求面积最值

柏黎平

殊途同归，巧求面积最值

柏黎平

分析各地中考试卷，可以发现不少以二次函数知识为背景的压轴题.二次函数在初中数学学习中占有重要地位，因其可以涵盖初中数学的所有知识点，具有较强的综合性，所以广受各地中考命题人员的青睐.

二次函数压轴题能考查综合运用知识的能力，具有知识点多、条件隐蔽、关系复杂、思路难觅、解法灵活等特点，因此是中考数学的难点.不过，如果我们能在做习题的基础上多总结一些方法，发现一些规律，有些难点就能较快突破.下面我们就一类二次函数与三角形面积的最值问题，来探求其中方法与规律.

一、规律发现

引例已知二次函数y=-x2+2x+3与x轴交于A、B两点（A左B右），与y轴交于点C，连接BC，点P为直线BC上方抛物线上一动点，求△PBC面积的最大值及此时点P的坐标.

图1

图2

【解析】本题为求三角形面积最值问题，可以采用平行线法或构造二次函数模型求最值等两种思路来解决问题.

解法1：如图1，易求直线BC的解析式为：y=-x+3，所以可设直线l为y=-x+b.过点P作直线l∥BC，则多数情况下，直线l与抛物线有两个交点，此时S△PBC显然不是最大；当直线l与抛物线有唯一交点（即方程有唯一解）时，点P到BC的距离最大，因此S△PBC最大.①代入②化为一元二次方程可得x2-3x+ b-3=0，当Δ=0时，方程有两个相等实数根，即.将b的值代回原方程组，可得此时点P的坐标为，再由P、B、C点坐标可求得△PBC的面积最大值为

解法2：如图2，同样求得直线BC的解析式为：y=-x+3.过点P作直线垂直于x轴，交直线BC于点D.

因为点P在抛物线上，所以可设点P坐标为（n，-n2+2n+3）（0≤n≤3），点D在BC上，因此坐标为（n，-n+3）；以PD为底边，设△PDC的高为h1，设△PDB的高为h2，则h1+h2=3，PD=（-n2+2n+3）-（-n+3）=-n2+3n.

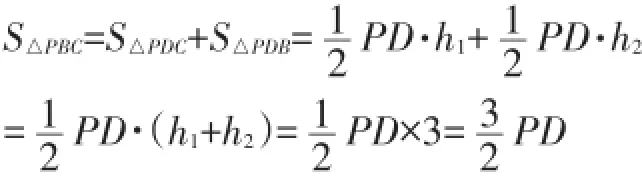
这样，S△PBC就是关于n的二次函数，根据二次函数性质易得当时，S△PBC的最大值，此时点P坐标为

【发现1】在解法1中，当三角形面积取得最大值时，只存在一个△PBC，但当面积缩小时，可能同时存在两个不同的△PBC；

【发现2】在解法2中，将△PBC进行纵向切割，将其分割为两个底边都为PD的三角形，它们的高的和就是BC两点的横坐标的差；

【发现3】注意观察两种解法中，当三角形面积取得最大值时，点P的横坐标是，而点C的横坐标为0，点B的横坐标为3，可以理解为点P的横坐标恰好是线段BC中点的横坐标.其实这种情况并不是巧合，是一种规律，是可以用数学方法证明的.（有兴趣的同学可以抛物线y=ax2+bx+c和直线y=mx+n（am≠0）的交点是（x1，y1），（x2，y2）为一般情况进行证明，这里就不赘述.）

二、试刀中考

例1（2016·江苏苏州）如图3，直线l∶y=-3x+3与x轴、y轴分别相交于A、B两点，抛物线y=ax2-2ax+a+4（a＜0）经过点B.

（1）求该抛物线的函数表达式；

（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值；

（3）略.

图3

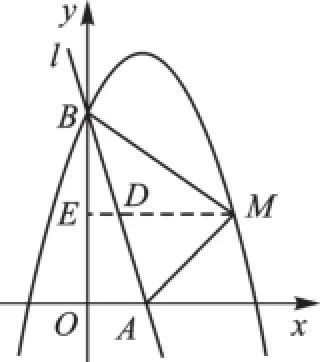
图4

【解析】（1）方法略，函数解析式为：y=-x2+ 2x+3；

（2）本题初看与上面的引例不同，但其抛物线上的动点，及计算三角形面积的最值都与引例类似，可用解法2的方法求解问题，不过考虑到纵向作垂线分割三角形计算有一定的困难，可以采用横向作垂线分割三角形，纵向距离为高.

如图4，过点M作ME⊥y轴于点E，交AB于点D，可设点M坐标为（m，-m2+2m+3），D在AB上，因此D坐标为：

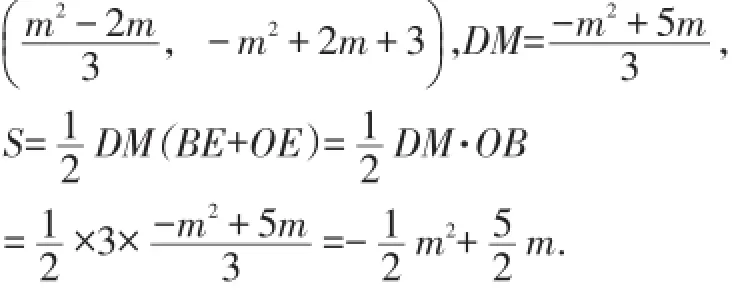
【评析】在平面直角坐标系中研究一些图形的面积时，可采用割补法将复杂、不规则的图形分割成若干个三角形计算.分割时要注意以下几点：①分割后的三角形面积应该容易计算；②一般的分割方法为横向或纵向；③如有必要，也可斜向分割.

如本题中也可连接OM，计算四边形BOAM的面积减△BOA的面积.有时可能要进行多次尝试，才能找到更为简单的计算三角形面积的方法.

（1）点A的坐标为_______，点C的坐标为________；

（2）线段AC上是否存在点E，使得△EDC为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；

（3）点P为x轴上方的抛物线上的一个动点，连接PA、PC，若所得△PAC的面积为S，则S取何值时，相应的点P有且只有2个？

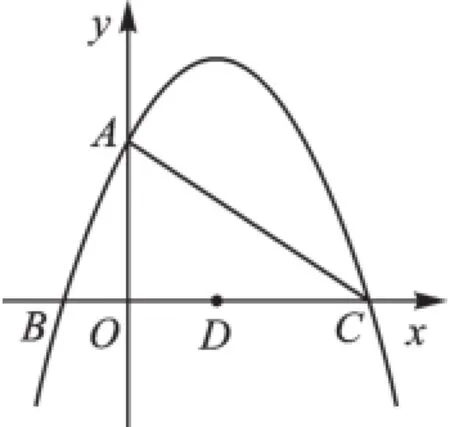
图5

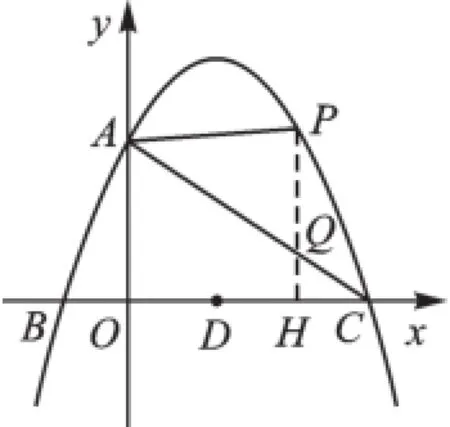
图6

【解析】（1）解答略，A（0，4），C（8，0）.

（2）易得D（3，0），CD=5.直线AC对应的解析式为，分三种情况讨论：①DE= DC，②ED=EC，③CD=CE，可求得三个点E的坐标分别为：E1（0，4）

（3）本题思路较为难觅，关键要理解“S取何值时，相应的点P有且只有2个”这句话的意思：其实只要考虑S的取值范围（即最大值与最小值），然后探讨在S取不同数值时的点P的个数即可.在求S的取值范围时，还要对点P所在的位置进行讨论，当点P的位置在AC上方时，就可以用引例中的两种方法求S的最大值，我们以第二种方法来解.

此时当且仅当S=16时，相应的点P只有1个，当0＜S＜16时，相应的点P有2个；

②点P在AB之间时，即-2＜m＜0时，易得S的最小值为0，最大值为20，且每个S的值都对应1个相应的点P.

故S=16时，相应的点P有且只有两个.

【评析】本题的第（3）题问法比较难理解，尤其是“相应的点P有且只有2个”，这需要对此问题有一定的研究经验，知道引例中的平行线研究方法的原理（关键是不同面积数值与点P的个数的对应关系），否则不容易联想到要考虑△PAC面积的取值范围.当然，在具体计算S的最大值时，还是用设坐标，用含m的代数式表示△PAC的面积的方法更为简洁一些.

值得一提的是，如果我们能想到引例中“发现3”揭示的规律，甚至可以更为简单地求出当点P在AC上方时S的最大值，即：当点P的横坐标取点A（0，4）和点C（8，0）的中点（4，2）的横坐标4时，△PAC的面积最大，于是可以迅速得出点P的坐标为（4，6），△PAC的面积就可以直接求，不必再用引例中的两种稍嫌复杂的方法解答.可见，当我们做多了习题后，若能注重对同类型的问题进行一般性的总结，往往可以得出实用的规律，帮助我们简化解题过程，从而节省计算的时间.

（作者单位：江苏省太仓市双凤中学）

扫描二维码，观看名师微课