从一道新的格点中考作图题的结构谈起
邹黎明(江苏省无锡市硕放中学)
浦叙德(江苏省无锡市新城中学)
从一道新的格点中考作图题的结构谈起
邹黎明(江苏省无锡市硕放中学)
浦叙德(江苏省无锡市新城中学)
利用格点特征作图在2015年中考试题中是一个亮点,对利用格点特征用无刻度的直尺作图进行了研究,从“品”2015年江苏省常州市一道中考作图题的结构出发,编拟出两道新的另类作图题.
中考命题;格点作图;无刻度的直尺
在2015年中考试题中,利用格点性质作图有多地采用,其与众不同的呈现方式给我们很多启发,这里从“品”2015年江苏省常州市一道格点作图题的结构出发,对于这类题目进行思考,编拟出两道另类作图题.
一、“品”中考试题
例1(2015年江苏省常州市第26题)设ω是一个平面图形,如果用直尺和圆规经过有限步作图(统称“尺规作图”),画出一个正方形与ω的面积相等(以下统称“等积”),那么这样的等积转化称为ω的“化方”.
(1)阅读填空.
如图1,已知矩形ABCD,延长AD到点E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.

图1
理由:连接AH,EH.
因为AE为直径,
所以∠AHE=90°.
所以∠HAE+∠HEA=90°.
因为DH⊥AE,
所以∠ADH=∠EDH=90°.
所以∠HAD+∠AHD=90°.
所以∠AHD=∠HED.
所以△ADH∽_____________.
即DH2=AD·DE.
又因为DE=DC,
所以DH2=____________,
即正方形DFGH与矩形ABCD等积.
(2)操作实践.
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图2,试用尺规作图作出与▱ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
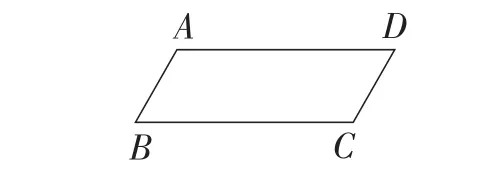
图2
(3)解决问题.
三角形的“化方”思路是:先把三角形转化为等积的_________________(填写图形名称),再转化为等积的正方形.
如图3,△ABC的顶点在正方形网格的格点上,试作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).

图3
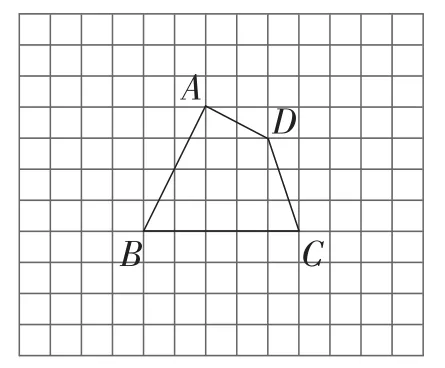
图4
(4)拓展探究.
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n-1边形,……,直至转化为等积的三角形,从而可以化方.
如图4,四边形ABCD的顶点在正方形网格的格点上,试作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).
解析:(1)△HDE,AD·DC.
(2)如图5所示.作法:①延长DA,过点B,C分别作BE⊥AD,CF⊥AD,垂足分别为点E,F;

图5
②延长AD到点G,使得FG=FC;
③以EG为直径作半圆⊙O;
④延长CF交半圆O于点H;
⑤以HF为一边作出正方形HFIJ,则正方形HFIJ为平行四边形ABCD的等积正方形.
(3)矩形.如图6,作法:①过点A作AD垂直BC于点D;
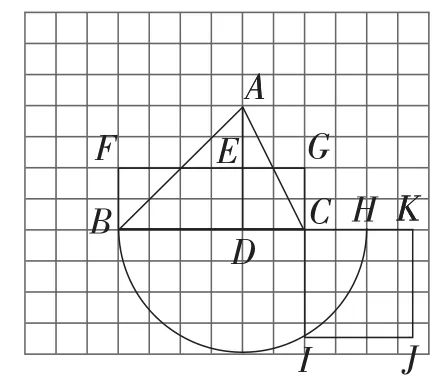
图6
②作AD的垂直平分线,取AD的中点E;
③过点E作BC平行线,作矩形BCGF,
则S矩形BCGF=S△ABC.
同(2)可以作出其等积正方形.
(4)如图7,作法:①连接BD,过点A作BD∥l;
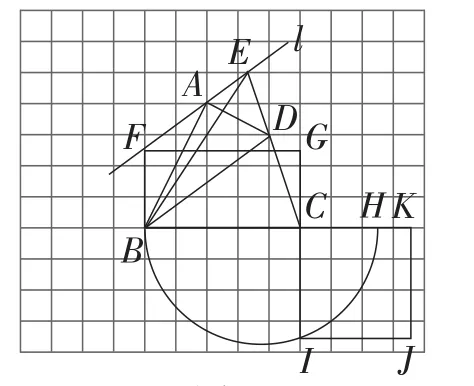
图7
②延长CD交直线l于点E;
③连接BE,则S四边形ABCD=S△EBC.
同(3)可以作出其等积正方形.
“品”题:这个新颖的题目给我们什么启发呢?从题目的结构进行思考,这是一个两段形式的题目,前面一半是一个性质的研究,后面则是利用性质或者这部分揭示的方法进行模仿作图.这个题目是阅读理解中感悟方法,是图形变换结合的作图题,考查了学生的理解能力、类比思想.
二、从结构上模仿编题
我们在研究猜想过程中,编拟了如下题目.


图8
(2)在(1)的条件下,HF垂直平分EG.求证:四边形EFGH是菱形.
知识应用:
(3)如图9,根据梯形ABCD在格点的特征作出一个菱形EFGH,使得点E,F,G,H分别在AB,BC,CD,DA上.并且AE∶EB=1∶2(只能用无刻度的直尺).

图9
解:(1)证明:在△AEM和△BEN中,
因为AD∥BC,

所以EM=GN.
(2)因为ME=GN,FH是EG的垂直平分线,
所以OE=OG.
所以OE+EM=OG+GN.
所以OM=ON.
因为AD∥BC,所以∠M=∠N.
因为∠MOH=∠NOF,
所以△MOH≌△NOF.
所以OH=OF.
因为OE=OG,
所以四边形EFGH是平行四边形.
因为EG⊥FH,
所以四边形EFGH是菱形.
显然这样的菱形有无数个.
(3)这个题目从图形格点特征,从AE∶EB=CG∶GD=1∶2,知道点E,G都是格点,还可以知道EG的中点也是格点.注意EG是一个2×8矩形的对角线,只要将这个矩形绕点O旋转90°,就可以作出EG的垂直平分线FH.如图10所示.

图10
进一步,我们给出一个限定作图问题.
(4)根据梯形ABCD在格点的特征作图,使得点E,G分别在AB,CD上.并且AE∶EB=CG∶GD=4∶5(只能用无刻度的直尺).
解:(4)如图11,作法:①在BC上取点M,使得CM=4,在AD延长线上取点N,使得DN=5,连接MN交CD于点G;
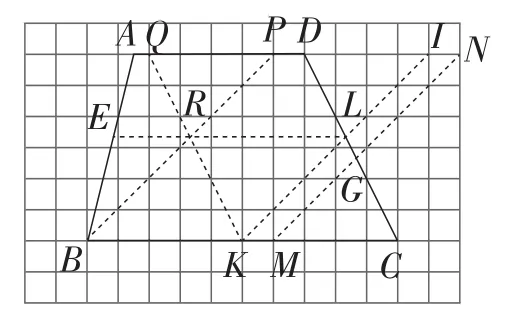
图11
②在BC上取点K,使得CK=5,在AD延长线上取点I,使得DI=4,连接KI交CD于点L;
③在AD上取点Q,使得DQ=5,在AD上取点P,使得QP=4,连接BP,QK相交于点R,作出直线LR,交AB于点E.所以点E,G作出.
如图12,如果我们连接EG,作出EG的垂直平分线,可以得到菱形EFGH.

图12
【点评】这个题目编拟的初衷是为了证明梯形的内接菱形有无数个.虽然没有完全解决猜想,现从例1的结构得到启发,编拟出一个利用性质作图的题目.这种性质加作图的素材只要我们留意,例如角平分线的有关比例的性质在教材中虽然已经不出现了,但是,我们可以提取这个知识点编拟出如下题目.
例3探索发现:
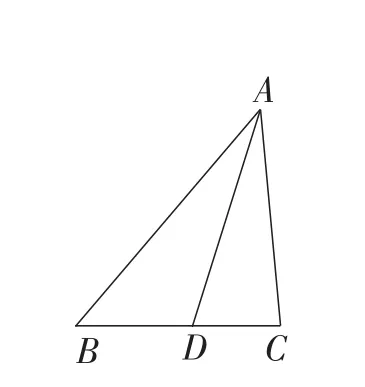
图13
知识应用:
(2)如图14,△ABC的顶点都是格点,作出∠ABC的平分线BD(用无刻度的直尺).
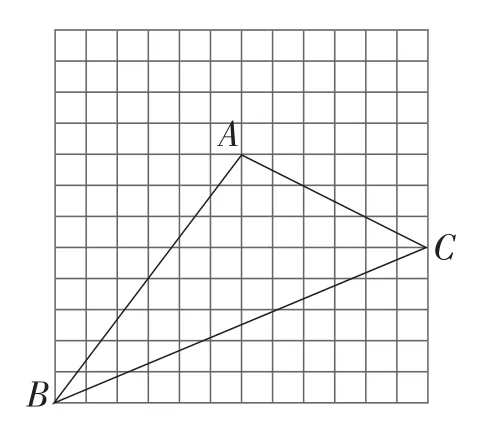
图14
解:(1)证明:如图15,过点C作CE∥AD交BA的延长线于点E,

图15
因为AD∥CE,

所以AC=AE.
所以∠ACE=∠E.
因为CE∥AD,
所以∠BAD=∠E,∠DAC=∠ACE.
所以∠BAD=∠DAC,
即AD平分∠BAC.
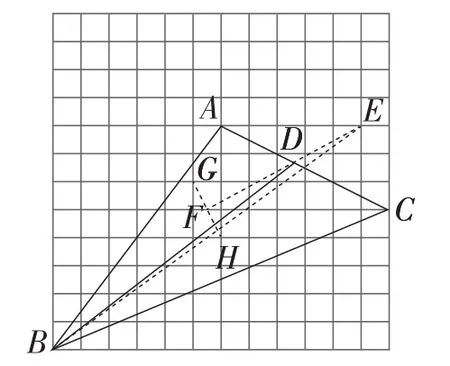
图16
【点评】2015年中考试题中有正方形网格作图的题目,一个新颖的题目或许能够成为今后的关注点,文中思考这种形式的另类作图题,例2、例3的编拟,这个专题或许能够给大家一点帮助.
三、“品”题的视角
“品”题是一种态度,它更加注重题目的结构,品结构就是题目本身价值的理解,数学题的价值在“品”中才能发现,是数学生命力的表现,我们数学呈现的一些思想和方法,或许不经意地在某些题目中若隐若现,往前一步海阔天高,看题说话,是一个人数学品质的聚焦.例1让我们体会模仿的形式,另外我们从题目中正方形网格这个载体,联系到无刻度尺作图,这种作图少了圆规,多了利用性质作图.这些赋予格点和平行线活力的作图问题使得几何更具魅力,应该关注几何的创新资源,把握问题的本质,编拟出符合《义务教育数学课程标准(2011年版)》要求的数学问题.
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]北京师范大学出版社,教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准(2011年版)》解读[M].北京:北京师范大学出版社,2012.
[3]邹黎明,顾泉洪.中考复习例说无刻度尺作图[J].中学生数学(初中),2015(6):43-44.
[4]王华.一道题的网络征解与研讨[J].中学数学教学参考(中旬),2014(10):60-62.
[5]浦叙德.浅谈数学课堂教学的生成性追问及时机[J].中国数学教育(初中版),2011(5):1-4.
2016—08—28
邹黎明(1964—),男,中学高级教师,主要从事初等数学中的几何不等式、中考命题研究.
——课堂的民主集中制

