浅谈反证法的可操作性——基于康托尔对角线法、哥德尔不完全性定理、图灵停机问题及EPR悖论

黄汝广

（深圳南天电力有限公司，广东 深圳 518000）

浅谈反证法的可操作性——基于康托尔对角线法、哥德尔不完全性定理、图灵停机问题及EPR悖论

黄汝广

（深圳南天电力有限公司，广东 深圳 518000）

一直以来，康托尔对角线法总是与反证法密不可分，然而反证法并不如通常看得那样简单。文章从操作主义的观点，针对反证法提出了几点可操作性的要求，然后分析了几个著名的反证法论证，发现都不同程度地存在一些问题。由于不恰当的隐性假设，康托尔关于实数集不可数的证明是无效的。哥德尔为证明不完全性定理而引入的一个定理违反了矛盾律，并且他关于“可证”与“真”的区分实际上是陷入了循环论证。图灵停机问题其实是比较晚近的提法，与图灵的原始论文有较大差别，而且有些证明思路可能还或多或少地误解了图灵。最后，通过分析爱因斯坦的EPR悖论，进一步强调了假设唯一以及事实认定，对于反证法的重要性。

反证法；可操作性；隐性假设；事实；康托尔对角线；哥德尔不完全性定理；图灵停机问题；EPR悖论

康托尔用来证明(0,1)不可数的对角线法，在数学史上可谓大名鼎鼎，有些文献也称之为逆对角线法或反对角线法[1]；之后，该方法在哥德尔不完全性定理以及图灵停机问题不可解的证明中，也立下了汗马功劳，同时还在悖论领域结出累累硕果，难怪有人赞誉其为永恒的金色对角线了。

然而，该方法自问世以来，也是一直争议不断。比如著名的哲学家维特根斯坦，就不承认康托尔与哥德尔的证明[2]。《古今数学思想》的作者克莱因，认为康托尔的证明，“在无意中陷入了引进说不清的定义的陷阱”，也即“一个要定义的东西是用包含着这个东西在内的一类东西来定义的”。诺贝尔物理学奖得主布里奇曼则经历了一个转变：开始时，他认同康托尔的证明，而30年后，当他从物理学经验中获得了操作的观点，重回到这一问题时，却发现自己再也无法心悦诚服了[3]。

事实上，康托尔对角线法总是与反证法密不可分，因此笔者更愿意称之为对角线反证法。而且，我们不要忘记，反证法本身也是很有争议的，比如布劳威尔等直觉主义者就不承认反证法的有效性。

从操作主义的观点看，一个有效的反证法或归谬法论证，应该符合下列要求：(1)首先，当然是要承认矛盾律和排中律；（2）推理过程有效，并能在有限步骤内完成，或者符合完全归纳法；(3)排除一切不当的隐性假设，也即待证命题的反命题应是推理中的唯一假设；(4)矛盾和假设必须有逻辑关系，一旦否定假设，矛盾应随之消除；（5）矛盾的导出必须涉及不依赖于假设的事实（有些事实由于众所周知，或者不言自明，在推理时经常被省略，我们可称之为“隐性”事实）。

后面三个条件的主要目的，是为了更好地确认矛盾的根源，是在于“假设”与“事实”不相容！当然，有人或许对（2）中的“有限步骤”不以为然，这可能是个见仁见智，也不用太纠结，只要保证推理有效即可。

下面，笔者将依据上述可操作性要求，对几个著名的反证法论证进行分析。

1 康托尔实数集不可数定理

康托尔关于(0,1)不可数的论证，大致如下[4]：假设(0,1)可数，并将其用十进制无限小数表示，可得如下一个无穷序列——

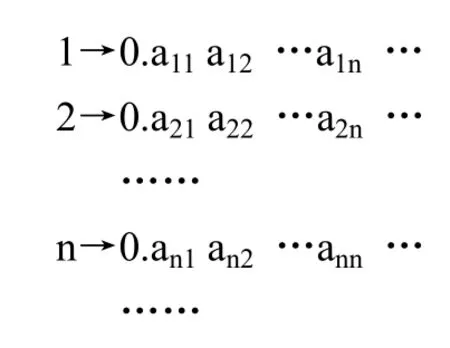
然后再构造数b=0.b1b2…bn…（当ann=1时，取bn=2；当ann≠1时，取bn=1）。康托尔认为，b属于(0,1)却不属于该序列，矛盾，故(0,1)不可数。

说实话，笔者对康托尔所谓“矛盾”的断言，是感觉有点莫名其妙：既然已经构造出了“属于(0,1)却不属于该序列”的数b，那就应该称之为“事实”才对，怎么反倒说是“矛盾”呢？

仔细分析上述论证，我们不难发现，康托尔的无穷小数序列只是对(0,1)的具体展示，两者完全等价：因此，属于(0,1)的一定也属于该序列，这个事实是如此不言自明，以至于康托尔都没有想到要交代一下。实际上，正是由于康托尔潜意识里一直坚持着这个“隐性”事实，他才认为“b属于(0,1)却不属于该序列”是矛盾。

然而，这种意义上的矛盾，只能是意味着：根本不存在“属于(0,1)却不属于该序列”的数b！不然的话，那就只能否定上述已经植根于康托尔潜意识的“隐性”事实，也即承认该序列只是（0，1）的真子集，或者说并非属于（0，1）的任何一个实数都能够写成无限小数的形式，整个实数理论都需要改写了。

问题出在哪里？事实上，数b既属于(0,1)也属于该序列，根本不存在什么矛盾！很显然，“b属于(0,1)”的结论，是纯粹由 b=0.b1b2…bn…自身形式决定的，应该不存在任何异议。那么，康托尔认为b“却不属于该序列”，是什么原因呢？这就要从构造数b的对角线法说起。

笔者认为，单纯依据对角线构造法，康托尔只能说 b在对角线之外（不被贯穿），而不能进一步推论b“却不属于该序列”。要推论b“却不属于该序列”，以下一个隐性假设是不可或缺的：康托尔对角线能够贯穿该序列的任何一个，也即可以遍历整个序列，不存在漏项问题。在这里，康托尔大概是被对角线的无限延伸性给迷惑了，以为对角线的无限延伸性，可以确保其遍历性。

然而事实并非如此。对于十进制小数，每一数位上都有十种不同的取值可能，这一事实注定对角线必然要漏项。先考虑属于(0,1)的所有n位小数，其序列只有n列但远远不止n行，而对角线却仅能贯穿n列n行，占总行数的比例很小；再令n趋于无穷大，即得到康托尔的无穷序列，但此时上述比例极限却为0：换言之，对角线无限延伸时，其漏项率几乎100%，而数b仅仅是其中之一；再形象点说，即b这条鱼虽然漏在了对角线这张渔网之外，但它仍然留在作为池子的无穷序列里。

更有趣的是，即便从康托尔的基数理论看，其对角线也必然漏项：因为(0,1)的基数是ℵ1，共有ℵ1个元素，但对角线只能贯穿ℵ0个；并且按康托尔的奇怪法则，应该有ℵ0/ℵ1=0，（ℵ1-ℵ0）/ℵ1=1，即漏项率可达100%。

因此，康托尔用以否定“假设(0,1)可数”的所谓“矛盾”，纯粹是子虚乌有，而且有点讽刺的是，按照康托尔的无穷集合理论，(0,1)反倒恰恰应该是可数的：在任一自然数前添加“0.”，可构造一个与之对应的小数，对所有自然数如法炮制，则构造出[0.1，1），它显然可数；再把[0.1，1）内所有数的第一位小数数字均减 1，则得[0，0.9）可数，（0，0.1）可数；故（0，1）=（0，0.1）∪[0.1，1）必然可数。

2 哥德尔不完全性定理

必须强调，康托尔对角线法针对的仅仅是数，如果说哥德尔不完全性定理的证明也使用了该方法，那它显然是被推广到命题了。对于数而言，尽管康托尔对角线法并不导致矛盾，然而将其推广到命题，却会导致否定式的自我指涉，其所得结果在本质上是一个矛盾式，也即“A=非A”。事实上，塔斯基正是利用这个矛盾式来定义空集的，也就是说，绝不可能存在满足它的任何东西；而哥德尔构造的所谓不可判定公式，实质上就是这样一个矛盾式。

当然，问题远不止于此，更加糟糕的是，在哥德尔的原始论文中，一个至关重要的所谓“定理Ⅴ”，其本身就会导致矛盾。该定理的内容如下[5]：

“对于所有递归关系R(x1,...,xn)，存在着n元关系符号r（含有自由变元 u1,...,un），使得对于所有的数的 n元关系组(x1,...,xn)，我们有

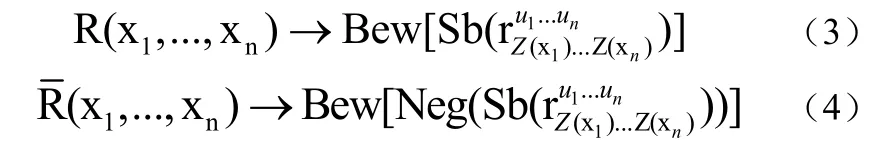
其中，Bew(x)表示 x是可证公式，Neg(x)表示 x的否定，的具体含义其实并不重要，关键是它在式（3）式（4）中完全相同，如果用 A来代替，那么就有Bew[A]与Bew[Neg(A)]。事实上，哥德尔还利用式（3）式（4）推导出了另外两对类似的式子（周训伟认为其推导是无效的[6]），这里的简化也同样适用。

该定理的问题在于，哥德尔居然要求式（3）式（4）同时成立，而且从哥德尔后面的论证看，也必须要求如此；否则的话，就不可能得到他所期望的结论。但是，在哥德尔的具体推理中，式（3）式（4）同时成立，最终将导致“A”与“Neg(A)”同时可证，而在哥德尔的理论中，“可证”的一定是“真”的：这也就是说，“A”与“Neg(A)”同时为“真”，显然违反了矛盾律！

有人争辩说，式（3）式（4）都是假言命题（笔者认为也许值得商榷），只看后件没有意义。当然，单纯看一个假言命题，只谈其后件确实没有意义，不过这个辩解对于哥德尔是不成立的：因为哥德尔的目的并非定理本身，他是要将其用于推理，以得到最终所期望的结论；然而，要把该定理用于推理，首先必须确定一个递推关系，但递推关系一旦确定，就肯定了前件，那么推理的结果必然要肯定后件——此时，所谓的“后件”已经实现了身份的转变，即由单纯假言命题的后件转化为了有效推理的结论。

事实上，在“定理Ⅴ”中，R(x1,...,xn)和(x1,...,xn)之间的关系是非常重要的：假如两者同时存在，则式（3）式（4）同时成立，但这最终会导致矛盾；假如两者不能同时存在，则式（3）式（4）也不能同时成立，因而不会导致矛盾。然而哥德尔并未采纳后者，因为如此一来，“17Genr不是可证的”与“Neg（17Genr）不是可证的”，就无法同时得到证明了，这会导致其最终目的落空；至于17Genr的具体含义，其实并不重要，这里只需明白：假如哥德尔的公理体系是完备的，则17Genr或Neg（17Genr）必定有一个可证；换言之，只要哥德尔证明17Genr与Neg（17Genr）均不可证，其公理体系就是不完备的，从而所谓的不完全性定理也就得到了证明。

另外，哥德尔的论证可能还涉及一个所谓的“万能定理”，即“从一个矛盾出发，结果可以是任何东西”。尽管哥德尔原始论文中并未明确提及这一点，但按照内格尔的说法，该定理与公理体系的一致性证明有密切关系：如果一个公理系统不是一致的，则每一个公式都是定理；反过来说，如果并非每个公式都是定理，则该公理系统是一致的[7]。

既然“定理Ⅴ”最终会导致矛盾，那么再加上这个所谓的“万能定理”，哥德尔无论推出什么结论，就都不足为奇了。更直白点讲，所谓不完全性定理，不过就是哥德尔先构造出一个固有的逻辑矛盾，然后再嫁祸于公理体系称其不完备而已。

退一步讲，假如哥德尔不完全性定理确实成立，那么最高兴的恐怕反倒应该是布劳威尔等人。因为如此一来，在哥德尔的公理体系内，命题会存在真、假、不可判定三种情况，排中律不再成立，反证法无效。但哥德尔不完全性定理的证明，却恰恰使用了反证法。

另外，哥德尔为了自圆其说，曾对“可证”与“真”做过如下区分——“可证”的都是“真”的，但“真”的未必都“可证”，因此存在不可证的真命题，“不可证”的未必都是“假”的。然而，这只不过是一个“循环论证”而已，因为上述辩解，实际上已经预先假设了不完全性定理的正确性。而且，在哥德尔的证明中，关于命题的两种不同划分——真假值与是否可证——也被混淆在一起了。

3 图灵停机问题不可判定定理

关于图灵停机问题不可判定的证明，也与对角线法大有关系，依据张再跃的《数理逻辑》，论证如下[8]：

“假设停机问题可解，则存在能行过程H，对任意程序 Pe与输入X，H能判断 Pe对输入X是否停机，设当 Pe对输入X停机时有H( Pe,X)=1，当Pe对输入X 不停机时有H( Pe,X)=0。利用H定义过程F：对任意自然数n，若H( Pe, n)=1，则F( n)=H( Pe,n )+1；若H( Pe, n)=0，则F( n)=0。因为过程H是能行的，所以过程F也是能行的，设计算F的程序编号为 e0，则F可表示为Pe0，即对任意n均有F( n)=Pe0(n)。接下来考察程序Pe0对输入e0的情况：若停机，则H( Pe0,e0)=1，从而F( e0)=Pe0(e0)+1≠Pe0(e0)；若不停机，则Pe0(e0)无定义，而由H( Pe0,e0)=0，却得F( e0)=0≠Pe0(e0)。上述矛盾表明，停机问题是不可解的。”

首先，既然“若H( Pe, n)=1，则F( n)=H( Pe, n)+1”，为什么不把H( Pe, n)=1代入，从而得出F( n)=1？（这里1和0是表示状态，故只能按布尔代数计算。）实际上，在笔者看来，拿“若H( Pe, n)=1，则F( n)=1”来对应“若H( Pe, n)=0，则F( n)=0”，是再自然不过的事：简而言之，即“F( n)=H( Pe, n)”！但如此一来，“若停机，则H( Pe0,e0)=1，从而F( e0)=Pe0(e0)+1≠Pe0(e0)”这个所谓的矛盾就不存在了。

其次，我们要问：按照定义，假如H( P1, n)=1，H( P2, n)=0，F( n)=？事实上，含两个独立变量的函数不太可能简化为只有一个独立变量！要避免这个问题，似乎只能这样定义——对任意自然数n，F( n)=H( Pn, n)；但这就需要Pn与n有某种确定的函数关系，比如Pn=T(n)：也即任给一个自然数 n，就可以通过函数T生成一个程序 Pn，而且没有程序是它不能生成的。显然，这个万能的程序生成机T，只能是个假设而已；然而由于这个隐性假设，从逻辑上讲，否定H就不再是唯一的选择了，除非你能实实在在地构造出这样一个T。

不过，关于图灵停机问题的通俗读物，更倾向于这样一种论证思路：利用万能图灵机H构造一个新程序D，它以H的输出为输入，若输入为1则不停机，若输入为0则停机；再用H来判定D，则总是导致矛盾。

很显然，这里的新程序D是一个自我否定的死循环。但我们要问的是，一个程序要如何界定？或者说，死循环真是程序吗？按照笔者个人的看法，一个程序的核心应该是其功能，没有任何功能的死循环，是错误而不是程序。

但我们也不妨退一步，假设死循环也是程序，那么在这个前提下，万能图灵机H就必须满足如下条件：能够判断死循环是不可停机的，并且整个判断过程不能触发死循环。然而，以H的输出为输入的死循环D却又必然会被触发。要消除这里所谓的矛盾，除了否定“万能图灵机H”外，否定“死循环是程序”同样可以达到目的，甚至我们还可以有第三个选择——自我否定式的死循环不是程序。

事实上，假设存在万能图灵机H，即使一个程序P对输入X不停机，我们也能将其改造为可停机的：先调用H判断P对输入X是否停机，如果判断停机，则对P输入X进行运算，并输出最终结果；如判断不停机，则不再对P输入X，而直接输出。

当然，万能图灵机H是不可能存在的，然而笔者认为这也是不可能被证明的，至少上述两种证明都不能让人满意。我们知道，在热力学上，不存在永动机其实只是能量守恒定律的一个等价表述；也许，在计算机领域，不存在万能图灵机应该被提升到公理的高度上来。

4 爱因斯坦的EPR悖论

这个著名悖论和康托尔对角线法之间，当然没有任何关系，而且也没有什么逻辑上的错误。但考察一下“EPR悖论”，对理解反证法是大有好处的：因为“假设”唯一与“事实”认定的重要性，在该悖论中体现的最为充分。

按照马克斯·雅默《量子力学的哲学》的分析，“EPR悖论”的论证包含了四个前提假设[9]：（1）物理实在性判据，（2）理论完备性条件，（3）量子力学的有效性，（4）相互作用的定域性。那么逻辑上讲，我们是可以否定上述任何一个假设，然而多个假设造成的结果，却是爱因斯坦和玻尔两人各说各话。

我们知道，爱因斯坦对量子力学的几率解释很不满意，他不相信上帝在掷骰子。其实在“EPR悖论”之前，爱因斯坦主要是否定量子力学的有效性，但被玻尔一一化解了，不得已，才承认其有效性，转而否定完备性：认为量子力学的几率描述，是由于漏了一个还未知的隐变量，而考虑隐变量的完备理论，将给出确定性描述[10]。

实际上，“EPR悖论”的关键是爱因斯坦认为量子纠缠态不合理，但量子纠缠态又是量子力学的必然推论，因此在逻辑上，他或许更应该否定其有效性，而不是完备性：否则，所谓的不完备性似乎就不是相对于隐变量理论而言的，倒更像是指适用范围的局限性（不过，这两种情况并不容易区分）。

本质上讲，数学中的“事实”都是构造性的，而物理上的“事实”却必须要由实验进行确认。在进行相关实验之前，也即事实还未确定的前提下，爱因斯坦要坚持其一贯的信念，却又不得不承认量子力学的有效性，那么否定完备性就是他唯一的选择。

多年之后，虽然实验并未站在爱因斯坦一边，但他关于量子纠缠态的计算被证明是正确的。认为爱因斯坦被偏见所误导，或者说玻尔比爱因斯坦更高明，这都是事后诸葛亮式的不公平之论：假如实验站在了爱因斯坦这一边，我们岂不是也可以同样来议论玻尔？实际上，玻尔的选择和爱因斯坦一样，也仅仅是要维持自己的一贯信念，并不是基于更深刻的洞察：因为这个问题只能交由实验来判决。最起码，玻尔在这个问题上的反驳，是远不如他之前反驳爱因斯坦的光子盒那样有说服力。

5 结论

反证法并不是万能的，即便承认矛盾律和排中律，其具体运用也不是我们通常想象的那么简单，这里有太多的陷阱。

实际上，整个反证法的真正核心，是在于对“事实”的认定。然而，推理中隐藏的不当假设往往会把我们引入歧途，以致张冠李戴，把其实毫不相关的假设做了替罪羊。

当一个反证法论证结束后，我们其实不妨再问问自己：否定这个假设，矛盾真的就可以消除么？如果否定假设，矛盾仍然存在，其结果就导致我们通常所谓的悖论；然而，这恰恰表明，矛盾与假设实际上无任何关系，我们应该转而审查论证中是否引入了不当的隐性假设。

当然，出问题的也未必是隐性假设，比如哥德尔居然就把一个固有逻辑矛盾作为了定理。至于“从一个矛盾出发，结果可以是任何东西”的所谓“万能定理”，根本就违背了推理的可靠性原则要求，应该从逻辑学中剔除之。

最后，不得不说，所谓永恒的康托尔金色对角线，实际上只不过是一件皇帝的新衣而已，在反证法中根本无用武之地。因此，笔者十分赞同张金成先生的呼吁：必须重新审视许多有名的反证法证明，尤其当其结论比较奇怪，或者在论证中使用了康托尔对角线、实无穷、不可数、连续统等概念的时候，更需要慎重对待[11]。

[1] 张建军.逻辑悖论研究引论(修订版)[M].北京:人民出版社,2014.

[2] 庄朝晖.基于直觉主义对哥德尔不完全性定理的评论[J].厦门大学学报(社会科学),2008(2):77-84.

[3] 杜丽燕,余灵灵.布里奇曼文选[M].余灵灵,杨富芳,译.北京:社会科学文献出版社,2009.

[4] 杜珣.现代数学引论[M].北京:北京大学出版社,1998.

[5] 陈波.逻辑学读本[M].北京:中国人民大学出版社,2009.

[6] 内格尔,纽曼.哥德尔证明[M].陈东威,连永君,译.北京:中国人民大学出版社,2008.

[7] 周训伟.哥德尔不完全性定理的证明过程有误[J].重庆工学院学报,2007,21(2):68-71.

[8] 张再跃,张晓如.数理逻辑[M]北京:清华大学出版社,2013.

[9] 马克斯·雅默.量子力学的哲学[M].秦克诚译.北京:商务印书馆,2014.

[10] 李晓.浅谈EPR悖论与量子纠缠[J].科技创新与应用,2015 (29):74.

[11] 张金成.超协调逻辑原理[M].北京:北京图书出版社,2015.

Introduction to the operability of reduction to absurdity——based on cantor diagonal method, Godel's incompleteness theorem, Turing downtime problems and EPR paradox

For a long time, cantor diagonal method and reduction to absurdity is inseparable, however, reduction to absurdity is not as simple as we usually think. According to the operating point of view, this paper puts forward some operational requirements in view of the reduction to absurdity. Then analyzed the text of several famous argument, found that there are some problems in varying degrees. Due to improper implicit assumptions, it is invalid that cantor prove real number set is uncountable. To prove incompleteness theorem, an important theorem of Godel introduced is a violation of the law of contradiction, and his excuse is a circular argument. Turing halting problem is relatively recent, but some of the popular view may be more or less misunderstood Turing. Finally, through the analysis of Einstein EPR paradox, further emphasized in reduction, assuming that the only recognized the importance of with the fact, for the reduction to absurdity, Einstein EPR paradox shows that the only assumption is very important.

the reduction to absurdity; operability; implicit assumptions; facts; Cantor diagonal; Godel's incompleteness theorem; Turing downtime issues; EPR paradox

G642

A

1008-1151(2016)09-0094-04

2016-08-10

黄汝广（1977－），男，山东人，深圳南天电力有限公司工程师。