Hom-李超代数的同调和非交换张量积

王 涵，张庆成

(东北师范大学 数学与统计学院，长春130024)



Hom-李超代数的同调和非交换张量积

王 涵，张庆成

(东北师范大学 数学与统计学院，长春130024)

本文给出了Hom-李超代数的非交换张量积的概念,得到了有关Hom-李超代数的同调及Hom-李超代数的非交换张量积的重要性质,丰富了Hom-李超代数的理论.

Hom-李超代数；同调；非交换张量积

2006年Hartwig,Larsson和Silvestrov为了更好的描述Witt代数和Virasoro代数提出了Hom-李代数[1]的定义, Hom-李代数理论对数学、物理学等领域的发展起到了十分重要的促进作用.在文献[2-4]中,Ammar和Makhlouf将Hom-李代数推广得到Hom-李超代数,并获得了重要的结果.随时间的推移,Hom-李超代数的一些性质和相关结果得到了广泛的研究,请参考文献[5-8],这丰富了李代数体系的研究内容.本文推广文献[9]和文献[10]的的相关内容,给出了Hom-李超代数的非交换张量积的概念,构造并研究Hom-李超代数的非交换张量积.

1 Hom-李超代数

a)[x,y]=-(-1)|x||y|[y,x]；

b)(-1)|x||z|[αL(x),[y,z]]+(-1)|y||x|[αL,(y),[z,x]]+(-1)|z||y|[αL(Z),[x,y]]=0；

则称(L,[-,-],αL)是一个Hom-李超代数.

其中(b)式称为阶化Hom-Jacobi等式,而且这个等式和下面的式子等价:

[αL(x),[y,z]]=[[x,y],αL(z)]+(-1)|x||y|[αL(y),[x,z]].

对于伴随表示adx=L→L,有adx(y)=[x,y],则阶化Hom-Jacobi等式可写成如下形式：

adαL(x)ady=ad|x,y|αL+(-1)|x||y|adαL(y)adx.

定义2【5】如果一个偶线性映射αL对任意x,y∈L有αL[x,y]=[αL(x),αL(y)], 则称Hom-李超代数(L,[-,-],αL)是保积的.

例1

a)定义1中,当αL=Id时,该定义即为李超代数的定义.因此李超代数是Hom-李超代数的一个子范畴,是一个特殊的Hom-李超代数.

b)令(A,μA,αA)是一个保积的Hom-结合超代数,如果对任意齐次元素x,y∈A有[x,y]=μA(x,y)-(-1)|x||y|μA(y,x),那么(A,[-,-],αA)就是一个保积的Hom-李超代数.

c)(L,[-,-])是一个李超代数,α∶L→L是一个李超代数自同态,定义[-,-]α∶L⊗L→L,对任意的x,y∈L，有[x,y]α=α[x,y]=[α(x),α(y)],那么(L,α)和括积[-,-]α一起构成了一个保积的Hom-李超代数.

定义3 设(L,[-,-],αL)和(L′,[-,-]′,αL′) 是Hom-李超代数, f∶L→L′是Hom-李超代数线性映射,若对任意x,y∈L满足:

a)f([x,y])=[f (x), f(y)]′；

b)f∘αL(x)=αL′∘f(x)；

则称f∶(L,[-,-],αL)→(L′,[-,-],αL′)是一个Hom-李超代数的同态映射.

如果两个Hom-李超代数(L,[-,-],αL)和(L′,[-,-]′,αL′)之间有一个同态映射f∶L→L′,且其为双射,则这两个Hom-李超代数同构.

保积的Hom-李超代数的同态映射是基本Hom-李超代数的同态映射.在下面的内容中,我们所提到的Hom-李超代数都为保积的Hom-李超代数.

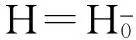
a)[x,y]∈H；

b)αL(x)∈H；

则称(H,αH)是一个Hom-李超子代数.

如果对任意x∈H,y∈L,有[x,y]∈H,那么(L,αL)的一个Hom-李超子代数(H,αH)叫做阶化Hom-理想.

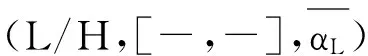
定义5Hom-李超代数(L,[-,-],αL)的中心是一个超子空间,有

Z(L)={x∈L|[x,y]=0,∀y∈L}.

注:当αL∶L→L是一个满的自同态映射时,(Z(L),αZ(L))是(L,αL)的一个阶化Hom-理想.同时在括积运算不发生混淆的情况下,记(L,[-,-],αL)为(L,αL).

定义6 设(L,αL)和(M,αM)是Hom-李超代数,一个偶的双线性映射ρ∶L⊗M→M,有ρ(x⊗m)=x·m,对任意齐次元素x,y∈H和m,m′∈M满足下面条件：

a)[x,y]·αM(m)=αL(x)·(y·m)-(-1)|x||y|αL(y)·(x·m)；

b)αL(x)·[m,m′]=[x·m,αM(m′)]+(-1)|x||m|[αM(m),x·m′]；

c)αM(x·m)=αL(x)·αM(m)；

那么称其为从(L,αL)到(M,αΜ)的Hom-作用.

在这些条件下,我们也说(L,αL)Hom-作用于(M,αM).

如果对任意x∈L和m∈M,有x·m=0,那么称Hom-作用是平凡的.

定义7 设(L,αL)是Hom-李超代数,如果(M,αM)是一个交换Hom-李超代数,并且有一个从(L,αL)到(M,αM)的Hom-作用,那么(M,αM)就是(L,αL)上的Hom-超模,即一个偶的双线性映射ρ∶L⊗M→M,有ρ(x⊗m)=x·m,对任意齐次元素x,y∈L和m,m′∈M满足下面条件：

a)[x,y]·αM(m)=αL(x)·(y·m)-(-1)|x||y|αL(y)·(x·m);

b)αM(x·m)=αL(x)·αM(m).

例2

a)L和M是李超代数,有一个从L到M上的李作用,那么(L,ld1)Hom-作用于(M,αM).

b)L是一个李超代数,α∶L→L是一个自同态,假设M是一个通常意义下的超模,且L到M上的作用满足对任意齐次元素x∈L和m∈M,有α(x)·m=x·m,则(M,αM)是Hom-李超代数(L,α)上的一个Hom-超模(参考例1(c)).

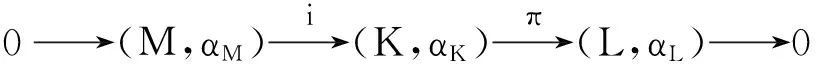
d)Hom-李超代数的交换序列是指Hom-李超代数的一个短正合列:

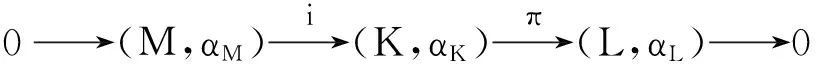
其中(M,αM)是一个可交换Hom-李超代数,满足αK∘i=i∘αM和π∘αK=αM∘π.通过定义ρ∶L⊗M→M,有ρ(l,m)=[k,m],且π(k)=l,则这个交换序列诱导出(M,αM)上的Hom-超模结构.

定义8 有两个Hom-李超代数(L,αL)和(M,αM),(L,αL)到(M,αM)上有一个Hom-作用,在基本向量超空间M⊕L上我们定义Hom-李超代数的半直积为(MãL,αã), 对任意齐次元素x,x1,x2∈L和m,m1,m2∈M满足

[(m1,x1),(m2,x2)]=([m1,m2]+αL(x1)·m2-(-1)|m1||x2|(αL(x2)·m1,[x1,x2])

(1)

且有自同态αã∶MãL→MãL使得αã(m,x)=(αM(m),αL(x)).

事实上,(MãL,αã)是一个Hom-李超代数,并存在一个Hom-李超代数的短正合列:

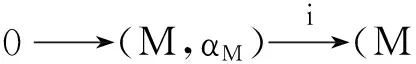
(2)

其中i(m)=(m,0),π(m,l)=l.同时(M,αM),是(MãL,αã)的一个阶化Hom-理想. 如果存在s∶,(L,αL)→(MãL,αã)使得s(l)=(0,l),则这个正合列是可分的.那么,正如例2(c)所述,若其满足l·m=i-1[(0,l),(m,0)]=i-1(αL(l)·m,0)=αL(l)·m,则存在(L,αL)到(M,αM)的Hom-作用.

定义9Hom-李超代数的一个同态映射∂∶M→L和(L,αL)到(M,αM)的Hom-作用,如果对任意齐次元素x∈L和m,m′∈M满足下列条件:

a)∂(x·m)=[x,∂(m)]；

b)∂(m)·m′=[m,m′]；

c)∂∘αM=αP∘∂；

那么就称这个同态映射为Hom-李超代数的交叉模.

例3

a)Hom-李超代数(L,αL)和其阶化Hom-理想(M,αM)之间的内射MP是一个Hom-李超代数交叉模.

b)如果(L,αL)是一个Hom-李超代数,(M,αM)是一个Hom-超模,则平凡映射0∶M→L是一个Hom-李超代数交叉模.

定义10 (M,αM)是一个Hom-李超代数(L,αL)上的Hom-超模,一个线性映射d∶L→M满足：

a)d([x,y])=(-1)|d||x|·αL(x)·d(y)-(-1)(|d|+|x|)|y|αL(y)d(x);

b)αM∘d=d∘αL;

称其为(L,αL)到(M,αM)的导子.

2 Hom-李超代数的同调

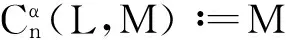
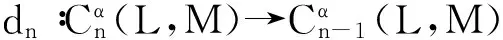
有

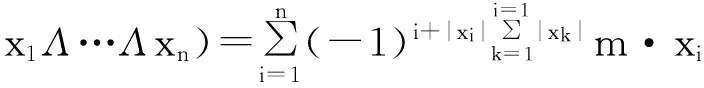
于是,系数在Hom-超模(M,αM)里的Hom-李超代数(L,αL)的同调表示为：

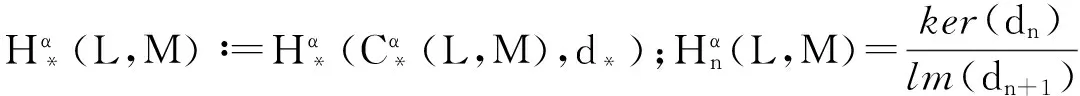
那么,由此可以计算一些低维的结果:

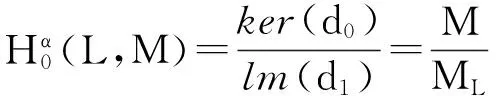
其中ML={m·l∶m∈M,l∈L}.

如果(M,αM)是一个平凡Hom-超模,即m·l=0,那么

3 Hom-李超代数的非交换张量积

a)(n·m)·n′=-(-1)|m||n|[m·n,n′];

b)(m·n)·m′=-(-1)|m||n|[n·m,m′];

则称Hom-作用是相容的.

例4 如果(H,αH)和(H′,αH′)是Hom-李超代数(L,αL)的阶化Hom-理想,则(H,αH)和(H′,αH′)之间的Hom-作用是相容的.

a)[m,m′]⊗αN(n)-αM(m)⊗m′·n+(-1)|m||m′|(αM(m′)⊗m·n)；

b)αM(m)⊗[n,n′]-(-1)|n′|(|m|+|n|)(n′·m⊗αN(n))+(-1)|m|n|(n·m⊗αN(n′))；

c)(n·m)⊗(m·n),其中|m|=|n|；

d)(-1)|m|n|(n·m)⊗(m′·n′)+(-1)(|m|+|n|)(|m′|+|n′|)+|m′|·|n′|(n′·m′)⊗(m·n)；

e)(-1)(|m|+|n|)(|m″|+|n″|)+|m|m|+|m′||n′|[n·m,n′·m′]⊗(m″·n″)+C·P·((m,n),(m′,n′),(m″,n″))；

其中C·P·((m,n),(m′,n′),(m″,n″))是(m,n),(m′,n′),(m″,n″))的轮换.

命题1 商向量超空间(M⊗N)/D(M,N)有括积运算

[m⊗n,m′⊗n′]=-(-1)|m||n|(n·m⊗m′·n′)

(3)

和由αM⊗N诱导的自同态映射(M⊗N)/D(M,N)→(M⊗N)/D(M,N),则(M⊗N)/D(M,N)是一个Hom-李超代数.

证明 很明显αM⊗N是对D(M,N)中的元素和式(3)所定义的括积运算保持封闭的,而这个括积和(M⊗N)/D(M,N)上定义的关系是一致的,并且可以从生成元扩展到任意元素.由于(M,αM)和(N,αN)间的相互的Hom-作用是相容的,则通过直接计算可知式(3)的运算满足定义1的(a)式和(b)式.

定义12 (M⊗N)/D(M,N)称为Hom-李超代数(M,αM)和(N,αN)的非交换张量积,为了方便记为(M★N,αM★N),且m⊗n等价类被记为m★n.

注:如果αM=IdM和αN=IdN,那么m★n是文献[9]中的李超代数M和N的非交换张量积.

Hom-李超代数的非交换张量积也可以通过泛性质来定义,如下面所示.

a)h[m,m′],αN(n)]=h(αM(m),m′·n)-(-1)|m|m′|h(αM(m′),m·n)；

b)h(αM(m),[n,n′])=(-1)|n′|(|m|+|n|)h(n′·m,αN(n))-(-1)|m|n|h(n·m,αN(n′))；

c)h(n·m,m′·n′)=-(-1)|m||n|[h(m,n),h(m′n′)]；

d)h∘(αM×αN)=αL∘h；

则称h是一个Hom-李超对.

例5

a)如果αL=IdL，αM=IdM和αN=IdN,那么定义13 就是文献[9]中李超对的定义.

b)设(M,αM)和(N,αN)是Hom-李超代数(L,αL)的两个阶化Hom-理想,那么双线性映射h∶(M×N,αM×αN)→(M∩N,αM∩N),满足h(m,n)=[m,n]是一个Hom-李超对.

定义14 对一个Hom-李超对h∶(M×N,αM×αN)→(L,αL),如果对任意其它一个Hom-李超对h′∶(M×N,αM×αN)→(L′,αL′),存在唯一一个Hom-超代数同态映射θ∶(L,αL)→(L′,αL′),满足θ∘h=h′,那么称h是广泛的.

这种情形下,如果h是广泛的,那么(L,αL)由(M,αM)和(N,αN)和它们的Hom-作用所决定的同构映射唯一确定.下面我们用Hom-李超代数的非交换张量积来描述它.

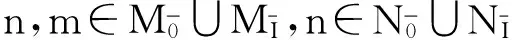
a)λ(m⊗n)=λm⊗n=m⊗λn;

b)(m+m′)⊗n=m′⊗n,其中m,m′有相同的阶;

m⊗(n+n′)=m⊗n+m⊗n′,其中n,n′有相同的阶;

c)[m,m′]⊗αN(n)=αM(m)⊗m′-n-(-1)|m|m′|(αM(m′)⊗m·n),

(αM(m)⊗[n,n′])=(-1)|n′|(|m|+|n|)(n′·m⊗αN(n))-

(-1)|m|n|(n·m⊗αN(n′)),d)[m⊗n,m′⊗n′]=-(-1)|m||n|(n·m⊗m′·n′).

命题2 如果Hom-李超代数(M,αM)和(N,αN)彼此平凡作用,且αM和αN是满同态,那么(M★N,αM★N)是一个交换Hom-李超代数且存在一个同构映射:

(M★N,αM★N)≅(Mab⊗Nab,αMab⊗Nab),

其中Mab=M/[M,M],Nab=N/[N,N]且αMab⊗Nab是由αM和αΝ所诱导的.

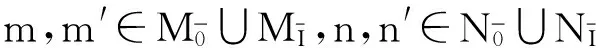
如果f∶(M,αM)→(M′,αM′)和g∶(N,αN)→(N′,αN′)是Hom-李超代数同态映射,并且(M,αM)和(N,αN),(M′,αM′)和(N′,αN′) 间的Hom-作用是相容的,使得f,g保持这些Hom-作用封闭,即：

则存在一个Hom-李超代数的同态

f★g∶(M★N,αM★N)→(M′★N′,αM′★N′),

满足(f★g)(m★n)=f(m)★g(n).

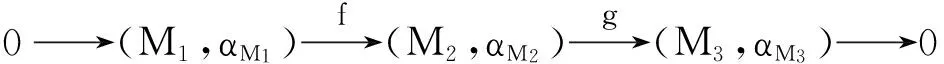
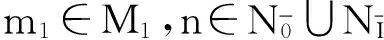
[f(m1)★n1,m2★n2)=-(-1)|m1||n|f(n1·m1)★m2·n2∈Im(f★idN).

因此g★idN诱导了一个分解：

事实上,这是一个Hom-李超代数同构映射,有反过来的映射：

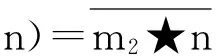
命题4 如果(M,αM)是一个Hom-李超代数(L,αL)的阶化Hom-理想,则存在一个Hom-李超代数短正合列：

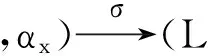
证明 我们知道是由投射(L,αL)→(L/M,αL/M)诱导出的一个函子同态,显然它是一个满射.令σ′：(M★L,αM★L)→(L★L,αL★L)和σ″：(L★M,αL★M)→(L★L,αL★L)是两个由内射(M,αM)(L,αL)和恒等映射(L,αL)→(L,αL)诱导的函子同态,知σ为单射.对任意的x∈M★L和y∈L★M，令σ(x,y)=σ′(x)+σ″(y)，这样是一个Hom-李超代数同态,τ∘σ是一个平凡同态.而Im(σ)是由元素m★l和l★m所生成的,其中齐次元素m∈M,l∈L.同时由公式(3) 知,它是一个(L★L,αL★L)的阶化Hom-理想.现在我们定义一个Hom-李超代数同态映射:

τ′:(L/M★L/M,αL/M★L/M)→(L★L，αL★L)/Im(σ).

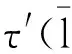
[1]HartwigJ,LarssonD,SilvestrovS.DeformationofLiealgebrasusingσ-derivations[J].JournalofAlgebra, 2006, 295(2): 314-361.

[2]Ammar F, Makhlouf A. Hom-Lie superalgebras and Hom-Lie admissible superalgebras[J].Journal of Algebra, 2010, 324(7): 1513-1528.

[3]Ammar F, Makhlouf A. Cohomology of Hom-Lie superalgebras and q-deforemed Witt superalgebra [J].Czechoslovak Mathematial Journal, 2013, 63(3): 721-761.

[4]Ammar F, Ayadi I, Mabrouk S, Makhlouf A. Quadratic color Hom-Lie algebras [J].Journal of Xinyang Normal University, 2012, 376(4): 174-195.

[5]Liu Yan, Chen Liang-yun, Ma Yao. Hom-Nijienhuis operators and T-extensions of Hom-Lie superalgebras [J].Linear Algebra and its Applications, 2013, 439 (7): 2131-2144.[6]Makhlouf A, Silvestrov S. Hom algebra structures [J].Journal of Generalized Lie Theory and Applications, 2008, 2(2): 51-64.[7]高宇佳,孙丽萍,刘文德. Hom-李超代数的结构[J].纯粹数学与应用数学,2014, 30(2): 186-194.

[8]李乐,徐晓宁.模李超代数的偶部生成元[J].琼州学院学报,2015,22(2):1-5.

[9]Garcia-Martinexcute X,Khamaladze E,Ladra M.Non-abelian tensor product and homology of Lie superalgebras [J].Journal of Algebra, 2015, 440: 464-488.

[10]Casas J, Khamaladze E, Rego N. A non-abelian tensor product of Hom-Lie algebras [J].Bulletin of the Malaysian Mathematical Society, 2014(2): 1-20.

(编校：曾福庚)

Homology and Non-abelian Tensor Product of Hom-Lie Superalgebras

WANG Han, ZHANG Qing-cheng

(School of Mathematics and Statistics, Northeast Normal University, Changchun 130024, China)

The definition of non-abelian tensor product of Hom-Lie superalgebras was proposed, and some important properties about homology of Hom-Lie superalgebras and non-albelian tensor product of Hom-Lie superalgebras were obtained. Thus, these results enriched the theory of Hom-Lie superalgebras.

Hom-Lie superalgebras; homology; non-abelian tensor product

2016-07-07

国家自然科学基金资助项目(11171055)；吉林省自然科学基金资助项目(20130101068JC)

王涵(1990-)，女，黑龙江佳木斯人，东北师范大学数学与统计学院2014级基础数学硕士研究生，主要研究方向为李理论.

张庆成(1960-)，男，吉林长春人，东北师范大学数学与统计学院教授，博士，主要研究方向为李理论.

O152.5

A

1008-6722(2016) 05-0044-06

10.13307/j.issn.1008-6722.2016.05.09