Robust visual servoing based Chinese calligraphy on a humanoid robot①

Ma Zhe (马 哲), Xiang Zhenzhen, Su Jianbo

(Department of Automation, Shanghai Jiaotong University, Shanghai 200240)



Robust visual servoing based Chinese calligraphy on a humanoid robot①

Ma Zhe (马 哲)②, Xiang Zhenzhen, Su Jianbo

(Department of Automation, Shanghai Jiaotong University, Shanghai 200240)

A robust visual servoing system is investigated on a humanoid robot which grasps a brush in Chinese calligraphy task. The system is implemented based on uncalibrated visual servoing controller utilizing Kalman-Bucy filter, with the help of an object detector by continuously adaptive MeanShift (CAMShift) algorithm. Under this control scheme, a humanoid robot can satisfactorily grasp a brush without system modeling. The proposed method is shown to be robust and effective through a Chinese calligraphy task on a NAO robot.

Chinese calligraphy, robust visual servoing, Kalman-Bucy filter, continuously adaptive MeanShift (CAMShift) algorithm.

0 Introduction

Nowadays robots are expected to provide specific entertainment and assistance for people[1-4]. Chinese calligraphy is an advanced skill as well as an art expressing the emotion and aesthetics of the author. Hence, it is critical to endow intelligent robots with the ability of performing Chinese calligraphy. Chinese calligraphy has a distinct characteristic. Since the brush of Chinese calligraphy is soft, its movements are in three dimensions instead of two. Because of this characteristic, slight changes in strength, orientation as well as moving speed exerted on the brush result in quite different effects. A thick stroke can be written through pressing the brush heavily[5]. Whether a sharp corner or a smooth corner can be formed in a stroke depends on how the author rotates the writing brush. A blurred stroke comes from fast speed[6]. This characteristic brings huge difficulties to Chinese calligraphy and simultaneously makes Chinese calligraphy an attractive art[7].

Many efforts have been made to enable robots to perform Chinese calligraphy. Yao, et al[6]presented a model of Chinese characters achieved through thinning the image, detecting the skeleton and modeling the skeleton with B-splines. Lam, et al[8]described a technique to generate stroke trajectories and applied it on a 5-DOF robotic art system. Zhang, et al[9]proposed a sensor management model, which is based on the fuzzy decision tree (FDT). The model can integrate necessary prerequisite knowledge of Chinese calligraphy and is verified on an Adept 604S manipulator.

Although previous work discussed above has achieved impressive performance, these efforts still have two mutual problems. All these researches are implemented on manipulators without human-robot interaction. Besides, the workspace is restricted by the fixed base of the robot. These shortcomings limit the performance and application of Chinese calligraphy on robots.

Fortunately, endowing a humanoid robot with the ability of Chinese calligraphy can avoid the two problems. A humanoid robot with the skill of performing Chinese calligraphy can teach children writing and amuse elderly people through interaction. Furthermore, the writing workspace of a humanoid robot is much larger than that of a manipulator due to its moving ability. In addition, a humanoid robot can keep learning different strokes through interaction with humans. Thence interaction based Chinese calligraphy on a humanoid robot is focused on.

Chinese characters of different styles and sizes are written with different kinds of brushes. Therefore it is essential for a robot to choose and grasp appropriate brushes in Chinese calligraphy task. There are some challenges for a humanoid robot to grasp a brush passed by a person. Compared with the models of a manipulator, less accuracy will be obtained by those of a humanoid robot, involving vision model and the relationship between visual space and workspace. Thence uncalibrated visual servoing control[10,11]is the key technique to ameliorate grasping performance. Besides, different from a manipulator which is fixed firmly on tables, a humanoid robot stands on two feet like human beings. Hence its whole body shakes slightly when its hand is moving, which brings noises obviously to images and disturbances to the motion system. Such noises and disturbances deteriorate visual servoing control. In addition, the brush handed by a person may move in an irregular track, which is a challenge for object detectors to handle.

In this work, an uncalibrated visual servoing system is investigated to conquer the aforementioned challenges and grasp a brush with a humanoid robot in Chinese calligraphy task. The influence of image noises, motion disturbances and irregular target movement is considered in the design process. Experiments are carried out with NAO robot[12]using the proposed approach.

The rest of this paper is organized as follows. In Section 1, a visual servoing system is presented, including the whole system structure, object detection technique based on CAMShift algorithm[13]and an uncalibrated visual servoing controller based on Kalman-Bucy filter[14]. Experiments on NAO robot, using the proposed method and the partitioned Broyden’s algorithm[15]are presented in Section 2, respectively, to verify the performance of the proposed method. Conclusions and future work are given in Section 3.

1 Robust visual servoing system

1.1 System structure

In Chinese calligraphy task, the humanoid robot is supposed to detect the brush passed by a person, grasp the brush and write Chinese character with it. Since there are image noises, motion disturbances and irregular brush trajectory in this task, robust detection and grasping are required. The CAMShift algorithm, which is robust to image noises and irregular target movement, is employed to detect and locate the brush. Meanwhile, the robust uncalibrated visual servoing technique based on Kalman-Bucy filter is applied to grasp the brush while overcoming both image and motion noises. The visual servoing system is proposed and depicted in Fig.1. The state estimator based on Kalman-Bucy filter estimates image Jacobian matrix by control quantity exerted on the robot and image features of robot end-effector. The image features are captured by CAMShift algorithm, and the image Jacobian matrix is used to calculate the control quantity for the next control period.

Fig.1 Robust visual servoing system

1.2 Object detection

CAMShift algorithm was derived from the earlier Meanshift algorithm[16]and aimed at detecting objects in continuous video. According to the CAMShift algorithm, the center of mass of the target object is calculated through MeanShift algorithm using color feature. The range of the target object in the current image is figured out by adjusting the size of the searching window, and this range information is used to set original searching window in the next image. By repeating this process, the target object is tracked continuously. The block diagram of the CAMShift algorithm is shown as Fig.2. The specific process of the CAMShift algorithm is as follows[13]:

Fig.2 Block diagram of CAMShift algorithm[12]

(1) Transform the captured RGB image into an HSV image.

(2) Set original tracking area of the target object, and set searching window.

(3) According to the MeanShift algorithm, pick up H(hue) channel from HSV images to form a new grey image. And histogram of a selected searching area in this grey image, called hue histogram of the corresponding area in the original image, is built. Taking this histogram as a searching table, channel H of the original image is mapped into a new grey image (back-projection image). Then the center of mass of searching area in this new image is calculated. Calculate two-order moment M02=∑u∑vv2·I(u,v), M20=∑u∑vu2·I(u,v), where u and v are the coordinates of the pixel in the image. Based on zero-order moment, one-order moment, two-order moment, deflecting angle of the target object can be calculated:

(1)

where ucand vcare the coordinates of the pixel in the image.

(4) Adjust the size of searching window according to the calculation below:

(2)

(3)

(4)

(5)

(6)

where r and s represent length and width of new tracking window, respectively.

(5) Determine whether the coordinate of the center of mass converges or not according to the MeanShift algorithm. If it converges, go to step (6), otherwise calculate new center of mass and set it as the center of searching window, then go to step (3).

(6) Output detection result, and update tracking window and searching window, then go to step (1).

The center of mass of the searching window represents the position of the object, which refers to the right hand of the robot or the brush in our task. The coordinates of this point will construct visual features and be used to calculate control quantity in the visual servoing control.

1.3 Uncalibrated visual servoing control based on Kalman-Bucy filter

To estimate image Jacobian matrix with Kalman-Bucy filter, the model of the visual servoing system should be transformed into the form of state function of linear system. The system state is formed with the members of image Jacobian matrix and the system output is the changes in visual features. Since Kalman-Bucy filter is tolerant of noises on system state and system output in a linear system, the visual servoing control method based on Kalman-Bucy filter is tolerant of the disturbances on the visual servoing system and noises on the images accordingly.

The model of the visual servoing system based on image Jacobian is defined as

(7)

where

(8)

Herein, m∈Rlpresents the visual feature of robot end-effector in images, p∈Rnrepresents the coordinate of robot end-effector in task space, L(p)∈Rl×nrepresents the image Jacobian matrix, which is unknown in uncalibrated visual servoing and needs to be estimated through Kalman-Bucy filter. Transforming Eq.(7) into a discrete form, the following is got:

m(k+1)≈m(k)+L(p(k))·△p(k)

(9)

A vector, x, is constructed with elements of the image Jacobian matrix as

(10)

y(x)=m(k+1)-m(k)

(11)

Treating x as the state vector, y as the output vector, and substituting Eqs(10),(11) into Eq.(9), the state function of the system is got:

(12)

where η(k), w(k) present process noise and measurement noise of the above linear system respectively, which are assumed to be independent white Gauss noises satisfying:

(13)

and

(14)

Then, the image Jacobian matrix is estimated as the state of system through Kalman filter[15]:

G(k+1)=F(k)+Rη

(15)

K(k+1)=G(k+1)H(k)T[H(k)G(k

+1)H(k)T+Rw]-1

(16)

F(k+1)=[I-K(k+1)H(k)]G(k+1)

(17)

(18)

After estimating the image Jacobian matrix, the control quantity to control end-effector of the robot can be calculated next. The control quantity in discrete form is got:

(19)

=2mo(k)-mo(k-1)

(20)

(21)

where

(22)

herein, △pmaxis the upper limit of moving velocity of robot’s end-effector, so the control quantity doesn’t exceed the robot’s moving capacity.

2 Experiments

A robust visual servoing system is presented for humanoid robots in this study. To verify this approach, a Chinese calligraphy task is designed and implemented in this section. This task includes two phases. The humanoid robot reaches for and grasps a brush handed to it by a participant in the first phase and writes Chinese characters with the brush in the second phase. The former phase is done using the visual servoing system described in this paper while the latter phase is finished with the motion generator through demonstration provided by Aldebaran Robotics.

The experiment platform is designed as shown in Fig.3. This system mainly consists of a NAO robot, a laptop and two USB cameras which are fixed on the NAO robot’s head. In the task, the NAO robot’s right arm is controlled to grasp the brush and write Chinese character with it. This arm has 6 DOFs including 2 in shoulder, 2 in elbow, 1 in wrist, and 1 in hand. Since there is no overlap between the NAO robot’s own view, two cameras are fixed manually on NAO robot’s head to endow the robot with stereo vision.

Fig.3 Experiment platform based on NAO robot

The visual servoing task on this platform is done through two parallel processes. One process is on laptop, which captures images, executes image processing and calculates control quantity. The other one is done by the NAO robot, which plans motion and controls robot’s right arm. Fig.4 is a schematic drawing that illustrates the two working parallel processes. Herein, the laptop captures images through two cameras and detects object from these images. Then the positions of the right hand of the NAO robot and the brush are got from the view of the two cameras. These positions are used as image features to estimate Jacobian matrix online for subsequent calculation. With Jacobian matrix, control quantity is calculated and sent to the NAO robot through Ethernet. Finally the NAO robot plans its motion and controls its right hand to reach for and grasp the brush.

Fig.4 Flow char of visual servoing control on the NAO robot

The values of essential parameters in the experiment are given in Table 1. Herein, the maximal velocity in the table represents the maximal velocity of the NAO robot’s hand in every coordinate direction. P(0), Rη, and Rware parameters in the visual servoing control method based on the Kalman-Bucy filter.

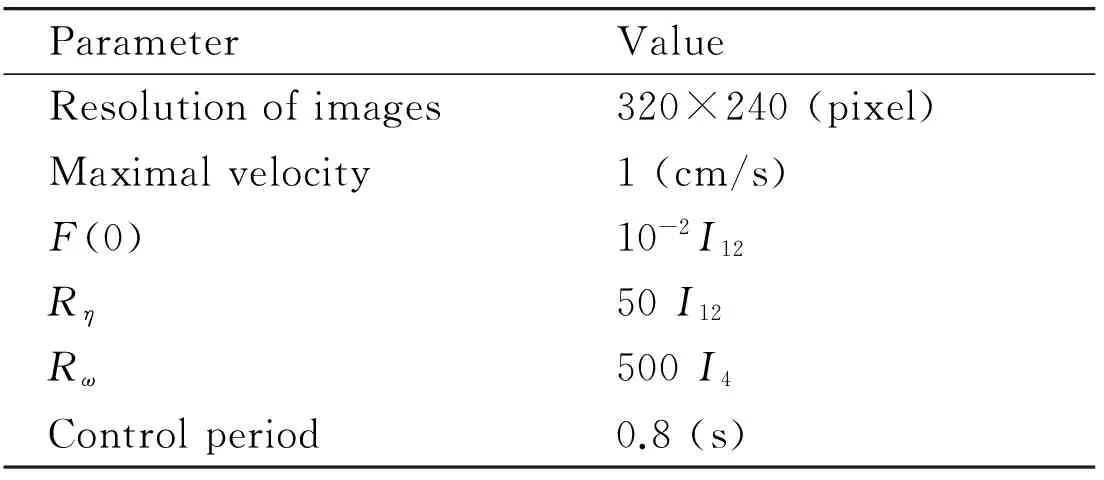
Table 1 Essential parameters for the experiment

2.1 Object detection

At the beginning, experiment is carried out to verify the robustness of the object detection technique in the tracking strategy proposed in this paper. In this section, the end-effector of the NAO robot's arm is controlled to move before a complex background consisting of objects of different shapes and colors. The CAMShift algorithm is utilized to detect and localize the moving end-effector in the image captured by one camera of the visual servoing system. The detecting result is shown in Fig.5, where a circle marks the detected end-effector and the center of the circle represents the position of the detected end-effector. It can be seen from the figure that the end-effector is detected correctly and the performance of the algorithm is rarely affected by the background. The position of the detected object changes within several pixels. It should be pointed out that the object is in the same color, with the end-effector in the background and the end-effector moves across the area in the image. Since hue (H) channel of the HSV image is employed in detection, the existence of the object brings challenge to this task. When the end-effector is moving by the object, the target area in CAMShift algorithm is extended to contain the object. Nevertheless, new addition in the area only adjusts the size in limited level. When the end-effector moves away from the red (ring) object, the target area is back to the end-effector.

Fig.5 End-effector detection in complex background

2.2 Brush grasping

In this experiment, the brush is moving in an irregular track in the workspace of the end-effector, and the velocity is around 1cm/s. The task is to detect, track and finally grasp the brush with robot’s right hand. After completing the task with the visual tracking strategy proposed in this study, a comparison experiment between our strategy and a classical visual servoing method[11]combined with CAMShift algorithm is carried out to verify the performance of the proposed strategy. To simplify calculation and raise tracking speed, marks are made on the robot's hand and target to be detected by cameras.

Original positions of NAO robot’s right hand in images are [172,168](pixel) for the left camera and [192,174] (pixel) for the right camera. Original positions of target object in images are [270,115] (pixel) for the left camera and [272,31] (pixel) for the right.

(23)

Fig.6 describes how NAO robot’s hand tracks the brush. During the task, the binocular vision system captures images of the task space. The NAO robot’s hand and the brush are detected and located in the images through the CAMShift algorithm according to the tracking strategy proposed in this study. Then the task is characterized in the visual space. At the very beginning, the image error between the mark on NAO robot’s hand and the brush is 111 pixels observed from the left camera and 163 pixels from the right camera. The image Jacobian is estimated according to Kalman-Bucy estimator iteratively, based on which control instructions are obtained. NAO robot’s hand tracks the mark on the brush with the control instructions. The control quantities are reducing as the distance between NAO robot’s hand and the brush becomes smaller. Finally, NAO robot’s hand reaches to the brush in 17 steps. Image errors between marks on NAO robot’s hand and the brush in the end of tracking process are within 10 pixels which are caused by the sizes of target object and NAO robot’s hand.

Fig.6 Brush tracking trajectories in the stereo vision system

The experimental results verify that the NAO robot can track a moving target accurately with its hand using the proposed visual servoing system. This approach is shown to be robust to image noises and disturbances caused by slight shake of NAO robot’s body and irregular object motion.

Then the proposed tracking strategy consisting of CAMShift algorithm and Kalman-Bucy filter-based visual servoing control method is compared with the partitioned Broyden’s method combined with CAMShift algorithm. NAO robot’s hand is controlled from the same position in the end-effector’s workspace to track the same point with these two strategies, respectively. The initial position of the hand’s end-effector observed from the two cameras are [184, 90] (pixel) and [198,112](pixel), respectively. The initial position of the target point observed from the two cameras are [129, 211] (pixel) and [132, 210] (pixel), respectively. The control results are shown in Fig.7. It can be seen from the figure that the strategy based on the partitioned Broyden’s method converges in 13 steps while the strategy proposed in this work converges in 11 steps. In addition, the tracking error in every direction in the image can reach 4 pixels using the partition’s method while error is within 1 pixel utilizing the proposed strategy. The visual tracking strategy presented in this study is validated to be accurate, fast and robust against noises and disturbances for such interaction task on humanoid robots.

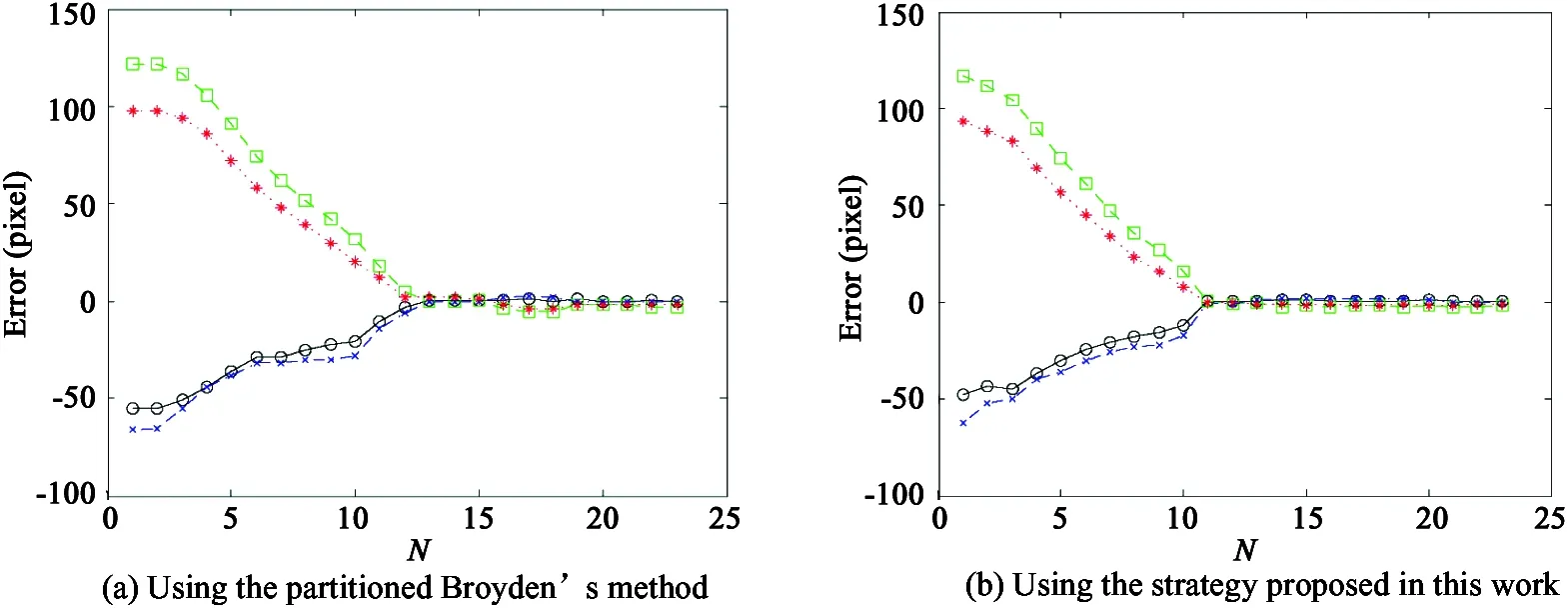
Fig.7 Tracking errors observed from two cameras

2.3 Writing with a brush

In this task, the NAO robot reaches for and grasps a brush handed to it with its right hand using the visual servoing system proposed in this study and writes Chinese characters on paper with the brush. The writing phase of the task is realized by motion generator through demonstration using Choregraphe software provided by Aldebaran corporation. The positions of NAO robot’s hand and the brush from the view of the two cameras in the beginning and the end of the task are shown in Fig.8, where red circles and green circles indicate NAO robot’s right hand and the brush detected by CAMShift algorithm described in this paper, respectively. The writing result is shown in Fig.9. These two characters, Jiao(交) and Da(大), are written according to the requirement of Chinese calligraphy, thereby reflecting certain meanings and emotions. The strokes and structures of these two characters are symmetrical, which is appreciated very much in the aesthetic of Chinese traditional civilization. The character, Jiao, which looks like a smiling face, indicates the ideal state of human beings in harmony with the whole world. The character, Da, reflects open mind with the extended strokes.

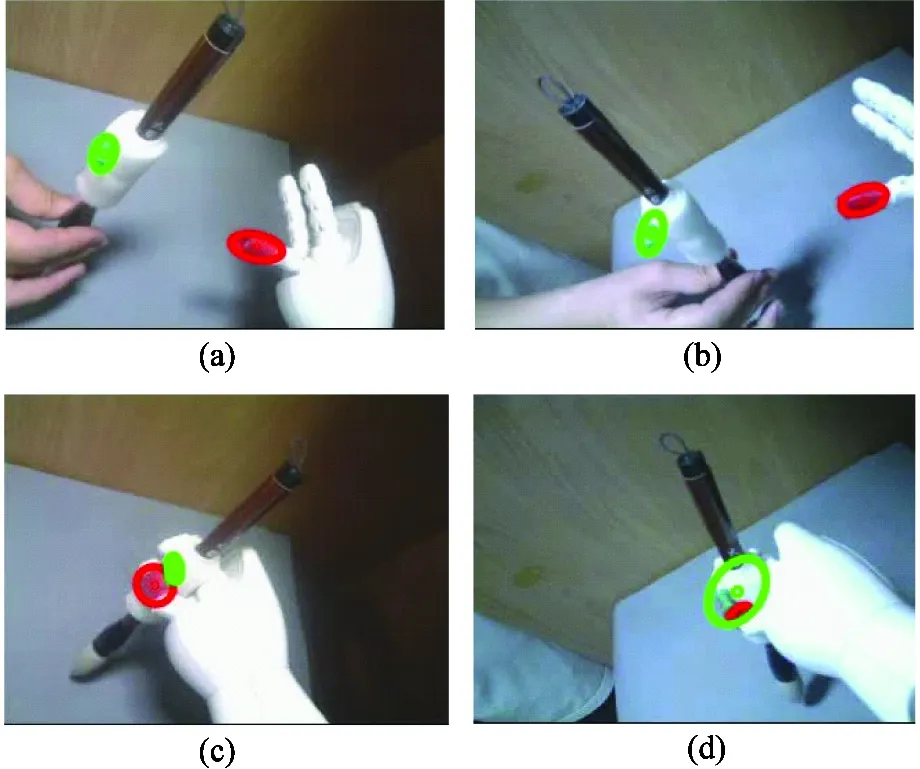
Fig.8 Images captured by two cameras before and after grasping. (a) is from left camera before grasping; (b) is from right camera before grasping; (c) is from left camera after grasping; (d) is from right camera after grasping

3 Conclusions

This work proposes a visual servoing system to grasp a brush with a humanoid robot in Chinese calligraphy task. The visual servoing controller in this system is based on Kalman-Bucy filter independent of system modeling, with the help of the object detector by CAMShift algorithm. With the proposed approach, NAO robot performs satisfactorily in Chinese characters task. Moreover, the results of the experiment indicate the robustness of the presented algorithm to noises in images, disturbances on motion system and irregular object motion.

Fig.9 Chinese characters written by the NAO robot

In the future, a humanoid robot is expected to learn how to write different strokes in Chinese characters without demonstration, but with help from humans through interaction.

Acknowledgement

Special thanks to Zhang Meng and Wang Lu for countless discussions and feedback leading to the development of this work. Many thanks to Zhao Yue and Chen Rui for their advice on the research topic and their help in implementing the experiments.

[ 1] Navarro S E, Marufo M, Ding Y, et al. Methods for safe human-robot-interaction using capacitive tactile proximity sensors.IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems, Tokyo, 2013, 1149-1154

[ 2] Xia G, Dannenberg R, Tay J, Veloso M. Autonomous robot dancing driven by beats and emotions of music. In: Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Valencia, Spain, 2012, 1: 205-212

[ 3] Barakova E I, Vanderelst D. From spreading of behavior to dyadic interaction-a robot learns what to imitate.InternationalJournalofIntelligentSystems, 2011, 26(3): 228-245

[ 4] Zhao Y, Su J. Sparse learning for salient facial feature description. In: Proceedings of the IEEE International Conference on Robotics and Automation, Hongkong, China, 2014. 5565-5570

[ 5] Lo K W, Kwok K W, Wong S M, et al. Brush footprint acquisition and preliminary analysis for Chinese calligraphy using a robot drawing platform. In: Proceeding of the IEEE International Conference on Intelligent Robots and Systems, Beijing, China, 2006. 5183-5188

[ 6] Yao F, Shao G. Modeling of ancient-style Chinese character and its application to ccc robot. In: Proceedings of the IEEE International Conference on Networking, Sensing and Control, Ft. Lauderdale, USA, 2006. 72-77

[ 7] Yao F, Shao G, Yi J. Extracting the trajectory of writing brush in Chinese character calligraphy.EngineeringApplicationsofArtificialIntelligence, 2004, 17(6): 631-644

[ 8] Lam J H M, Yam Y. Stroke trajectory generation experiment for a robotic Chinese calligrapher using a geometric brush footprint model. In: Proceedings of the IEEE International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009. 2315-2320

[ 9] Zhang K, Su J. On sensor management of calligraphic robot. In: Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 2005. 3570-3575

[10] Hutchinson S, Hager G D, Corke P I. A tutorial on visual servo control.IEEETransactionsonRoboticsandAutomation, 1996, 12(5): 651-670

[11] Piepmeier J A, Lipkin H. Uncalibrated eye-in-hand visual servoing.TheInternationalJournalofRoboticsResearch, 2003, 22(10-11): 805-819

[12] Gouaillier D, Hugel V, Blazevic P, et al. Mechatronic design of NAO humanoid. In: Proceedings of the IEEE International Conference on Robotics and Automation, Washington, USA, 2002. 769-774

[13] Qian J, Su J. Online estimation of image jacobian matrix by kalman-bucy filter for uncalibrated stereo vision feedback. In: Proceedings of the IEEE Intenational Conference on Robotics and Automation, Washington, USA, 2002, 1: 562-567

[14] Bradski G R. Computer vision face tracking for use in a perceptual user interface. In: Preceeding of the IEEE Workshop Application of Computer Vision, Princeton, USA, 1998. 214-219

[15] Piepmeier J A, Lipkin H. Uncalibrated eye-in-hand visual servoing.TheInternationalJournalofRoboticsResearch, 2003, 22(10-11): 805-819

[16] Cheng Y. Mean shift, mode seeking, and clustering.IEEETransactionsonPatternAnalysisandMachineIntelligence, 1995, 17(6): 790-799

Ma Zhe, was born in 1988. She is currently a Ph.D candidate in the Department of Automation, Shanghai Jiaotong University. She received her B.S. degree from Xi’an Jiao Tong University in 2010. Her research interests include visual servoing control and human robot interaction.

10.3772/j.issn.1006-6748.2016.01.005

① Supported by the National Natural Science Foundation of China (No. 61221003).

② To whom correspondence should be addressed. E-mail: mazhe.sjtu@gmail.comReceived on Apr. 3， 2015