Research on the adaptive hybrid search tree anti-collision algorithm in RFID system①

Jin Xiaofang (靳晓芳), Liu Mengxuan, Shao Min, Jin Libiao, Huang Xianglin

(Information Engineering, Communication University of China, Beijing 100024, P.R.China)



Research on the adaptive hybrid search tree anti-collision algorithm in RFID system①

Jin Xiaofang (靳晓芳)②, Liu Mengxuan, Shao Min, Jin Libiao, Huang Xianglin

(Information Engineering, Communication University of China, Beijing 100024, P.R.China)

Due to more tag-collisions result in failed transmissions, tag anti-collision is a very vital issue in the radio frequency identification (RFID) system. However, so far decreases in communication time and increases in throughput are very limited. In order to solve these problems, this paper presents a novel tag anti-collision scheme, namely adaptive hybrid search tree (AHST), by combining two algorithms of the adaptive binary-tree disassembly (ABD) and the combination query tree (CQT), in which ABD has superior tag identification velocity and CQT has optimum performance in system throughput and search timeslots. From the theoretical analysis and numerical simulations, the proposed algorithm can colligate the advantages of above algorithms, improve the system throughput and reduce the searching timeslots dramatically.

anti-collision, adaptive binary-tree disassembly(ABD), hybrid search tree, discrimination

0 Introduction

Nowadays, radio frequency identification (RFID) technology is widely used in the automated identification system[1]. A general RFID system is comprised of a reader and a lot of tags. The reader recognizes an object through wireless communications with the tag which has a unique identification (ID) and is attached to the object[2,3]. However, if tags send signals to the reader at the same time, they will collide with each other. Thus, an efficient anti-collision algorithm is needed to reduce the collision timeslots and increase the system throughput effectively.

The RFID anti-collision algorithm can be classified into two categories: tree-based algorithms and Aloha-based algorithms[4,5]. This paper focuses on the former one because the tree-based algorithms have 100% identification efficiency. As studied in Ref.[6], tree-based protocols are based on the collision resolution algorithm. In the binary tree algorithm (BT), when a set of tags causes collisions, the mechanisms split them into two subsets and attempt to recognize them in turn[7]. Therefore, theQ-ary tree would be split intoQsubsets.

Based on the tree protocol, a lot of improved algorithms have been produced[5,6]. Sun[8]proposed an improved anti-collision algorithm based on the regressive style, and the algorithm took a quad tree structure when continuous collision bits appeared. An improved adaptive multi-tree search anti-collision algorithm (IAMS)[9]optimized the prefix which was set by the reader to reduce the idle timeslots, and through the collisions, the IAMS could choose the search tree adaptively. Although the above algorithms could choose the optimum search tree adaptively, the methods of selecting tree are limited only by using binary tree and quad tree. The optimal system efficiency could be obtained by using the 3-ary search tree[10]. The adaptive binary-tree disassembly (ABD) anti-collision algorithm in Ref.[11] grouped the tags adaptively. However, the query method still used the fixed binary tree. The combination query tree (CQT) anti-collision algorithm in Ref.[12] adjusted the query tree according to the length of tags, but it was not adaptive to vast tags. The performance of the ABD and the CQT algorithms did not achieve a desired effect.

In order to achieve ideal performance, this paper synthesizes the advantages of ABD which has the superior tag identification velocity and the CQT which has the optimum throughput and search timeslots. Thus an adaptive hybrid search tree (AHST) algorithm is proposed. The simulations testify that the AHST algorithm has the least search timeslots and the highest throughput.

The rest of this paper is organized as follows: Section 1 introduces the ABD and the CQT algorithms briefly. In Section 2, the AHST anti-collision algorithm is presented by analyzing the concept, formula and procedure. In Section 3, simulation results verify advantages of the new algorithm. Conclusions are showed in Section 4.

1 Analyses on original tree-based algorithms

1.1 The adaptive binary-tree disassembly anti-collision algorithm (ABD)

According to signals received by the reader from tags (e.g., readable, idle or collision), the reader transmits feedback to inform the tags about what happens during the last cycle in the BT principle. When the feedback is collision, the tags involved in this collision generate a binary number randomly and add this number to their counter, where the initial value is 0.

Fig.1 is an example of the BT.

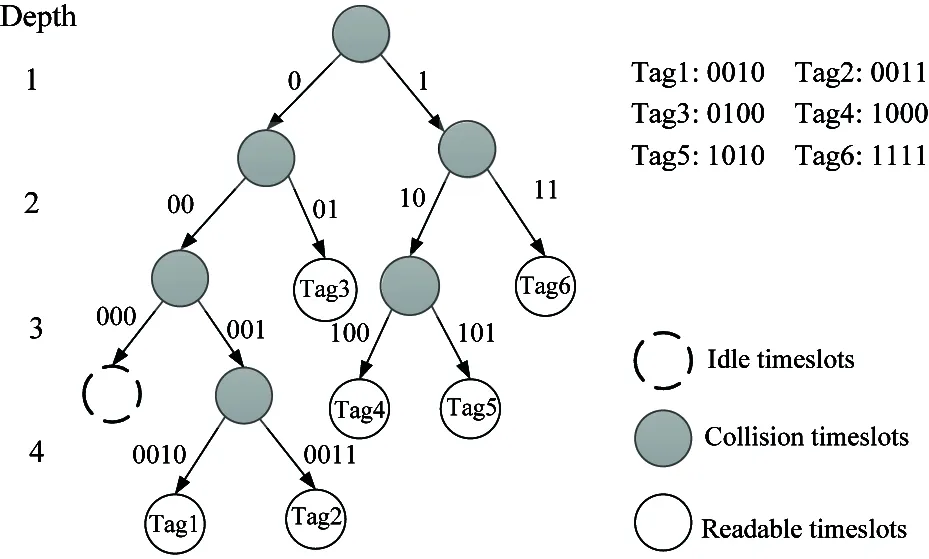
Fig.1 Tag identification procedure of the BT

The ABD anti-collision algorithm has tag identification efficiency better than the BT algorithm in the first layer of depth. The timeslots are divided into three parts:

(1) Readable timeslots: only one tag transmits its signals to the reader and then this tag is recognized by the reader.

(2) Idle timeslots: no tag transmits information. This timeslot is wasteful and should be reduced.

(3) Collision timeslots: more than one tag transmit their signals to the reader, so that the reader could not recognize any one of them.

The ABD algorithm splits 2ltimeslots at the first layer of depth. l is defined as discrimination and increases adaptively when the number of tags increases. The number of sub-binary trees can be decided by the number of collision timeslots at the first layer of depth, the idle timeslots needn’t to be dealt with again, and the readable timeslots can recognize tags directly. Then, the remaining tags will be recognized till all tags are identified using the binary-tree algorithm.

Fig.2 is an example of the ABD algorithm when l=2.

Suppose N tags are identified by the reader and the IDs of these tags are random distribution. T represents the timeslots which are needed to identify all tags. S stands for the throughput which is defined as N/T×100% and reflects the efficiency of the communication channel.

Fig.2 Tag identification procedure of the ABD (The discrimination of the first depth is 2)

In the BT algorithm[13]:

TBT=N([log2N]+1)

([]: round up to an integer)

(1)

(2)

In the ABD algorithm:

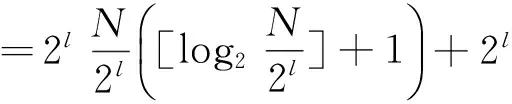
=N([log2N]-l+1)+2l

(3)

(4)

Tsub=TBT-TABD=Nl-2l

(5)

It is seen clearly that when N increases, the ABD algorithm effectively decreases the number of search timeslots, and then increases the throughput[11].

1.2 The combination query tree (CQT)

The combination query tree (CQT) is based on the 3-ary tree principle. In Ref.[10], the authors showed that the 3-ary tree had the optimum performance, but only when the length of the ID of a tag is the multiple of 3. In order to tackle this disadvantage, the CQT algorithm proposes a novel protocol which is suitable for tags with random length.

In the 3-ary query tree algorithm, it is needed to convert binary to ternary. The conversion process is called the binary convert to ternary (BCT). The basic mechanism of the BCT algorithm is shown in Table 1.

Table 1 The mechanism of binary convert to ternary

The conversion methods of CQT are showed as follows:

(1) If the ID length of the tags is the multiple of three, it can convert to ternary directly，so these tags can be identified using the 3-ary tree algorithm.

(2) If the tags’ ID length is divided by three and the remainder is one bit, the tags can be just identified by 3-ary tree algorithm. For example, two tags here: (0100) and (0101), are converted into ternary numbers: (020) and (021), the tags will collide each other after the algorithm recognizes 02, then the tags will only leave one number, namely 0 or 1. Thus, the algorithm can directly identify one from the other.

(3) If the tags’ ID length is divided by three and the remainder is two bits, such tags can be identified by the combinations of 3-ary tree algorithm and 2-ary tree algorithm. The 3-ary tree algorithm will be used to deal with the whole number and the remainder can be identified by the 2-ary tree algorithm.

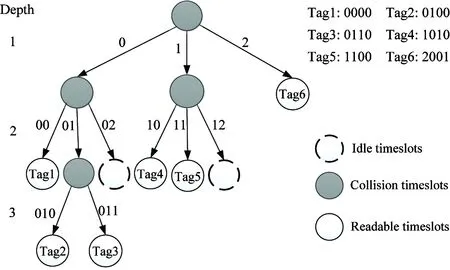
Fig.3 Tag identification procedure of the CQT

Fig.3 is an example of the CQT in which the reminder is two bits. There are six tags whose ID lengths are 5 bits, which are (00000), (00100), (00110), (01110), (10000), and (11001). The conversions of binary to ternary are (00 00), (01 00), (01 10), (10 10), (11 00), (20 01). The implementations of this algorithm are showed in Fig.3.

2 The adaptive hybrid search tree anti-collision algorithm (AHST)

The new algorithm aims to take the advantages of both ABD and CQT algorithms. First, system encodes the IDs of the tags as described in Part 2.2. Second, in the first search layer of depth, the system splits the search tree. Last, the system selects binary tree or 3-ary tree according to the new IDs. The new algorithm can achieve higher efficiency with large scale tags in RFID system.

Fig.4 shows the frame diagram of the AHST:

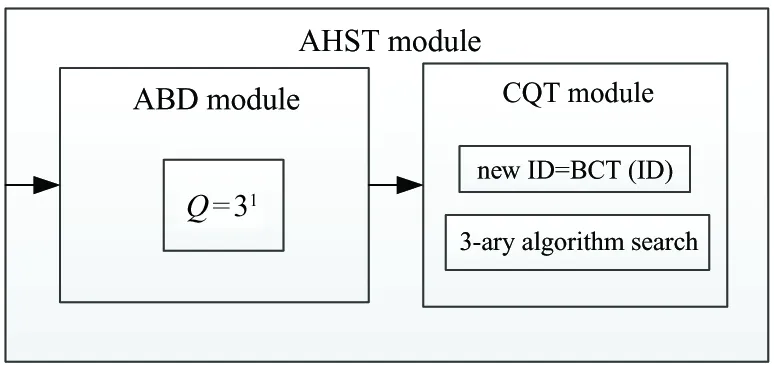
Fig.4 Frame diagram of the AHST

2.1 Principle and process

All the specific procedures are showed as follows:

1. The reader splits Q=3lat the first layer of depth (1≤l≤L, L represents the length of tags). The reader sends query codes with l within the relevant time, tags with the same code respond to the reader.

2. The reader determines the number of 3-ary trees at the second layer of depth according to the number of collision timeslots. No tags exist in the idle timeslots which needn’t to be handled again. A tag can be identified directly in the readable timeslots.

3. In the second layer of depth, tags are identified by using the CQT algorithm. According to the different lengths of tags’ ID, they can be converted into different new IDs.

The tags that have the new IDs are identified by using the 3-ary tree algorithm.

4. The reader examines whether the sub-3-ary tree is the last one. If it is not the last one, it will be returned to the third procedure.

2.2 Formula and proof

In the 3-ary tree principle[7]:

TBS=N([log3N]+1)

([]: round up to an integer)

(6)

(7)

As the length of tags is L, when mod(L,3)=0, the search process is 3-ary tree, then

=N([log3N]-l+1)+3l

(8)

(9)

When mod(L,3)=1, the last layer of search tree is binary tree and only one bit needs to be identified. The remaining average of the search timeslots is 1 besides the 3-ary search timeslots of the previous layers. So

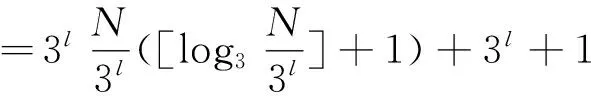
=N([log3N]-l+1)+3l+1

(10)

(11)

When mod(L,3)=2, the last layer of the search tree is a binary tree and only two bits need to be identified. The rest tags can be searched by using the 2-ary tree algorithm, in which the timeslots is 2n-1. However, in this system, there is an overlap between the first node of the 2-ary tree and the previous node in the 3-ary tree, so the timeslots have to be 2n-2. By means of the formula 2n-2, it is easily concluded that when there is only one tag left, the timeslot that needed for identifying the tags is 0. When there are two tags, the timeslot is two. Three tags, four timeslots, four tags, six timeslots, thus, the average number is (0+2+4+6)/4=3. So

=N([log3N]-l+1)+3l+3

(12)

(13)

So

(14)

According to the formula above, the search timeslots and throughputs could be calculated. So in the next part, it only needs to analyze the condition of mod(L,3)=2, like Fig.3. However, the discrimination l is unknown, so it is necessary to find the optimal l within different ranges of tags.

Theoretically, l should increase with the increase of the number of tags and it could be calculated via Eq.12 above.

l=2, T1=N([log3N]-2+1)+32+3

l=3, T2=N([log3N]-3+1)+33+3

l=4, T3=N([log3N]-4+1)+34+3

l=5, T4=N([log3N]-5+1)+35+3

and

T1=T2, N=18

T2=T3, N=54

T3=T4, N=162 are got.

By the simulation of the formula, best selection of l is got. Table 2 describes the optimal value of l with different number of tags, and the same value from Fig.6 in the next part could be got.

Table 2 Selections of l

3 Algorithm simulation and performance analyses

In order to compare different deterministic algorithms and find the optimal one within different ranges of tags, this paper tests the identification efficiency and the scopes of the discrimination l of the AHST algorithm.

3.1 The comparisons of four algorithms

According to the formula in Section 2 and 3, the performance of the AHST algorithm compared with the BT, the ABD and the CQT is evaluated, the variation range of tags from 0 to 500 is set, and the length of tags is chosen as 5.

Fig.5(a) presents the relations between the number of tags and the search timeslots. Fig.5(b) presents the relations between the number of tags and throughputs.

(a) Comparison of search timeslots when l=5

(b) Comparison of system throughput when l=5

As shown in Eq.14, the search timeslots are related to [log3N], since it is discontinuous integers, there are sharp fluctuations at some points. As showed in Fig.5(a), the search timeslot of AHST is the lowest among the other algorithms with the increasing number of tags. When systems are stable, search timeslots of the new algorithm decreases by 52.5%, 37.5%, 26.5% compared with the BT, the ABD and the CQT algorithms.

Fig.5(b) shows that the system throughput of the AHST is the highest among the BT, the ABD and the CQT algorithms. When systems are stable, the new AHST algorithm has the throughput 3.45 times higher than the BT algorithm, and 2.45 times, 1.62 times higher than the ABD and the CQT algorithms respectively.

3.2 The optimum selection of l within different ranges of tags

In the AHST algorithm, l represents the discrimination which is unknown. When the number of tags is large, this algorithm can reduce search timeslots and improve system throughput effectively. When the number of tags is small and the allocations of initial timeslots are too many, the performance of the algorithm would decline obviously. Thus, finding optimal l within different ranges of tags is very important. Fig.6 presents the relations between the number of tags and discrimination l. The simulation results verify the validity of the theoretical analysis like Eq.14 in Section 3. Discrimination l is set as 2, 3, 4, and 5 respectively.

As is shown in the Fig.6(a), with the increase in the tags, systems with different l have different efficiency. Fig.6(b) is a partial enlarged drawing of the Fig.6(a). From Fig.6, it is concluded that when the number of tags is less than 18, l=2 requires the least search timeslots. When the number of tags is between 18 and 54, l=3 performs better. When the number of tags is between 54 and 162, l=4 performs better. When the number of tags is larger than 162, l=5 performs better, and it can forecast that there will be more crossover points with the increase in the tags. The result is the same as the described situation in Table 2.

4 Conclusion

This study presents a novel tag anti-collision algorithm, which performs effectively for large scale tags in RFID system. By using the AHST, a decrease in the search depth leads to a decrease in the search timeslots effectively. At the same time, the 3-ary search tree algorithm is used which has the efficiency better than the other Q-ary search tree algorithms. Theoretical analyses and simulated experiments in Part 4 prove the validity of the AHST algorithm. That is when the number of tags is large, the new algorithm can improve the system efficiency effictively. Search timeslots of the new algorithm decreases by 52.5%, 37.5% and 26.5% compared to the BT, the ABD and the CQT algorithms. Meanwhile, the system throughput is 3.45 times, 2.45 times and 1.62 times higher than the BT, the ABD and the CQT algorithms. At last, the optimal intervals of discriminationlare confirmed. So AHST is a complete solution and is proved to be the optimal scheme.

(a) Search timeslots of new protocol with different l

(b) The blowup of picture (a)

Reference

[ 1] Amira S, Hania H, El-Sayed E. A new proposed anti-collision algorithm for RFID. In: Proceedings of the 30th National Radio Science Conference, Cairo, Egypt, 2013. 424-429

[ 2] Liu X H, Qian Z H, Zhao Y H, et al. An adaptive tag anti-collision protocol in RFID wireless systems.InformationSecurity, 2014, 11(7):117-127

[ 3] Yang Q, Li J Ch, Wang H Y, et al. An anti-collision algorithm using tag random-dispersing for RFID system. In: Green Computing and Communication, 2013 IEEE and Internet of Things, IEEE International Conference on and IEEE Cyber, Physical and Social Computing, Beijing, China, 2013.1077-1080

[ 4] He Y J, Wang X Y. An ALOHA-based improved anti-collision algorithm for RFID systems.IEEEWirelessCommunication, 2013, 20(5):152-158

[ 5] Huang Y H, Chen X R. Dynamic slots collision tracking tree based RFID anti-collision algorithm. In: Proceedings of the 10th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 2014. 662-669

[ 6] Wang X, Jia Q X, Gao X, et al. Effective RFID anti-collision algorithm based on 3-ary collision-track tree.JournalofHuazhongUniversityofScienceandTechnology(NatureScienceEdition), 2014, (6): 73-78 (In Chinese)

[ 7] Shin J M, Jeon B C, Yang D M. Multiple RFID tags identification with M-ary query tree scheme.IEEECommunicationsLetters, 2013, 17(3):604-607

[ 8] Sun W Sh, Hu L M. Anti-collision algorithm for adaptive multi-branch tree based on regressive-style search.JournalofComputerApplications, 2011, 31(8): 2052-2055 (In Chinese)

[ 9] Zhang X J, Cai W Q, Wang S P. One anti-collision algorithm based on improved adaptive multi-tree search.ActaElectronicaSinica, 2012, 40(1): 193-198 (In Chinese)

[10] Mathys P, Flajolet P. Q-ary collision resolution algorithms in random-access systems with free or blocked channel access.InformationTheory, 1985, 31(2):217-243

[11] Ding Z G. Research and realization on key technologies of RFID: [Ph.D dissertation]. Hefei: University of Science and Technology of China, 2009. 68-77 (In Chinese)

[12] Jiang Y, Zhang R N. An adaptive combination query tree protocol for tag identification in RFID systems.IEEECommunicationsLetters, 2012, 16(8):1192-1195

Jin Xiaofang, born in 1980. She is a Ph.D candidate in the area of the digital signal processing in the Communication University of China. She received her M.S. degree from Communication University of China in 2006. Her research interests are digital signal processing and the areas of RFID.

10.3772/j.issn.1006-6748.2016.01.015

① Supported by the National Natural Science Foundation of China (No. 61401407).

② To whom correspondence should be addressed. E-mail: myjinxf@sohu.comReceived on Dec. 22， 2014