Selective transmission and channel estimation in massive MIMO systems①
Yang Ruizhe (杨睿哲), Zong Liang, Si Pengbo*, Ma Dawei, Zhang Yanhua*
(*Beijing Advanced Innovation Center for Future Internet Technology, Beijing University of Technology, Beijing 100124, P.R.China)(**College of Electronics Information and Control Engineering, Beijing University of Technology, Beijing 100124, P.R.China)
Selective transmission and channel estimation in massive MIMO systems①
Yang Ruizhe (杨睿哲)②***, Zong Liang**, Si Pengbo***, Ma Dawei**, Zhang Yanhua***
(*Beijing Advanced Innovation Center for Future Internet Technology, Beijing University of Technology, Beijing 100124, P.R.China)(**College of Electronics Information and Control Engineering, Beijing University of Technology, Beijing 100124, P.R.China)
Massive MIMO systems have got extraordinary spectral efficiency using a large number of base station antennas, but it is in the challenge of pilot contamination using the aligned pilots. To address this issue, a selective transmission is proposed using time-shifted pilots with cell grouping, where the strong interfering users in downlink transmission cells are temporally stopped during the pilots transmission in uplink cells. Based on the spatial characteristics of physical channel models, the strong interfering users are selected to minimize the inter-cell interference and the cell grouping is designed to have less temporally stopped users within a smaller area. Furthermore, a Kalman estimator is proposed to reduce the unexpected effect of residual interferences in channel estimation, which exploits both the spatial-time correlation of channels and the share of the interference information. The numerical results show that our scheme significantly improves the channel estimation accuracy and the data rates.
multiple-input multiple-output (MIMO), selective transmission, time-shifted pilots, Kalman
0 Introduction
Massive multiple-input multiple-output (MIMO) is a new breakthrough communication technique, which is based on the conventional MIMO features unprecedented numbers of service-antennas with a high ratio of service-antennas to terminals, channel state information derived from uplink pilots and time division duplex (TDD) reciprocity[1]. When MIMO arrays are made large, both opportunities and challenges[2]are met. The opportunities include increased capabilities of exploiting propagation channel, inexpensive low-power components built with the robustness to the interference. However, as one of the challenges, the effect of pilot contamination on massive MIMO appears to be much more profound than in classical MIMO, which results in a considerable channel estimation error by reusing pilots from one cell to another[3]. In addition, the favorable independent propagation that the Massive MIMO relies is not quite true. In reality, the MIMO channels are generally correlated because the large antenna arrays are not sufficiently well separated or the propagation environment does not offer rich enough scattering[4-6].
To tackle the challenge of the pilot contamination, effective channel estimations exploiting the channel characteristic are proposed[7,8]. In Ref.[7], an eigenvalue decomposition-based approach estimates the channel blindly from the received data just with a short training sequence to resolve the scalar ambiguity in the covariance matrix of the received signals. In Ref.[8], in the uplink training a rank-q channel approximation method based on compressive sensing is proposed. On the other hand, power control[9,10]and coordinated pilots assignment[11]are used to mitigate the pilot contamination. In the coordinated approach[11], users in different cells having the small channel correlations with each other are assigned to the same pilots, so that the pilot contamination is minimized. Different from the work in the traditional transmission with aligned pilots mentioned above, time-shifted pilots are proposed in Refs[12,13] to avoid pilots simultaneous transmission in adjacent cells, and it is possible to completely cancel the effect of interferences from the data to pilots on the assumption that the channels between the infinite antennas are independent. Later in Ref.[14], the performance improvement using time-shifted pilots under the effect of a finite number of antennas is confirmed. Also in the case of finite antennas, a zero-forcing transceiver is employed to resolve the interferences using time-shifted pilots Ref.[15]. However, as it is known that zero-forcing schemes eliminate the interference by orthogonalizing the channels, which brings loss of channel gains and is therefore inappropriate for the strong channel correlation environments.
In this study, the multicell massive multiuser MIMO using time-shifted pilots for the physical channels is investigated. Over these channels, the interferences become considerable for both the aligned pilots and time-shifted pilots transmissions. Here, the interferences in transmissions using time-shifted pilots is analyzed and a selective transmission is proposed, where parts of users are selected to temporarily stop downlink transmitting during a particular period. Using the proper selection, the strong interference from these selected users to the uplink pilots in adjacent cells is alleviated. Moreover, to improve the system performance under the residual interferences, a Kalman estimator is proposed to filer out both interferences and noise based on the time-spatial correlation of the channels and the share of the interference information.
1 System model
It is considered a network of L cells with full spectrum reuse. In each cell the base station with M antennas services K single-antenna users.
1.1 Physical channel model
Using the physical channel model, the channels in thet-th block (block-fading) from user k in thel-th cell to the base station (BS) in thel′-th cell can be represented as
(1)
where the angular domain is divided into a large but finite number of directions P. Each direction is associated with a steering vector a(θl′klp) with the random angle-of-arrival (AOA) θl′klp,
a(θl′klp)=[1,e-jf1(θl′klp),…,e-jfM-1(θl′klp)]T
(2)
Also using the physical channel model in Eq.(1), the channel hk′l′kl(t) is obtained from user k in thel-th cell to user k′ in thel′-th cell during time block t, as shown in Fig.1.

Fig.1 Channels in the case of two cells
Let Hl′ldenote the channel matrix between the BS in thel-th cell and the BS in thel′-th cell, which is assumed to be time invariant due to the fixed locations of the BSs[16].
(3)

(4)

1.2 Signals in the uplink and downlink
A TDD massive MIMO system is considered using time-shifted pilots, see Fig.2. Assume that the uplink pilots of length τ are mutually orthogonal within a cell and therefore intra-cell interference is negligible in the channel estimation phase. The pilot sequence sk=[sk1sk2…skτ]Tused by user k, k=1,2,…,K, |sk1|2+…+|skτ|2=τ is assumed.

Fig.2 Time-shifted pilot scheme with G=3 groups
For simplicity, cell l*in the 1st group is considered as the target cell, and the interference from the adjacent cells is only considered in this section, see the gray area in Fig.2, while other interferences will be explained in Section 2.3.
During the pilot phase, the M×τ signal received at BS l*is

+N0
(5)

In the downlink of both the 1st group and 3rd group when users in the 2nd group are sending pilot sequences, the received signal at user k*in cell l*can be written as

(6)

In the simultaneous uplink, BS applies signal processing with the receiving vector. Since the received signal in the uplink has similar formation to the downlink Eq.(6) but without I2, on the downlink analysis is focused, and the extension to uplink can be straightforward.
2 User selection and channel estimation
2.1 Interference analysis
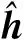
(7)
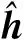
Proposition 1 The effect of interferences depends on the positions of the interfering users and the interfered user in their respective serving cells and also the relative positions of these serving BSs. Specifically, the interact of these positions directly depends on the angles, including θl*kl*pθl′k′l′p′, φl*l′p and θl*l′p, as well as the variances of the propagation coefficients.
Proof: Using physical channel model, the interference in Eq.(5) can be derived as
(8)
with

(9)
(10)
The derivations in Eqs(8)~(10) show that the effect of interferences not only depends on the relationship between θl*kl*p and θl*l′p in Eq.(10) but also the relationship between φl*l′p and θl′k′l′p′in Il*k′l′ Eq.(9). Thus, for the sensitive users who have the strong correlation between a(θl*kl*p) and a(θl*l′p), a better way to deal with the interfering is to reduce the interferences from the strong interfering users, which can be defined by the expectation of cos(θl′k′l′p′)-cos(φl*l′p). Specifically, only when |θl′k′l′p′±φl*l′p|>0, these inter-cell interference on the pilots can be minimized, which will be analyzed in Section 2.2.

Proposition 2 The interference in the downlink transmission is mainly caused by the other downlinks both in the same cell and in adjacent cells. The effects of these interferences depend on the positions of both interfering users and interfered users, especially their AoAs, e.g., θl*k′l*p and θl*k*l*p′. Fortunately, the interferences from the uplink pilots in other cells are minor interferences when ρkl≤Pkland even can be ignored.
Proof: Using physical channel model, interference I1in Eq.(6) can be written as

(11)
with

(12)

(13)
and interference I3is rewritten as
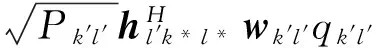
(14)
with
(15)

2.2 Selective Transmission
Proposition 1 and Proposition 2 show that the problems of using time-shifted pilots are the interferences between pilots and data. Several approaches can mitigate interferences, including user selection and power allocation. Although the primary scenario of such studies is the traditional multiuser MIMO systems[17], the algorithms can be applied in this paper, where SINR can be obtained according to Section 3. However, these selections involve matrix operations of high computation complexity in large antenna array systems. Besides, the algorithms based on current channels cannot be directly used for the pilots transmission selection. Furthermore, even based on statistic spatial correlation, the traditional simple user reducing may lead to blind zone. Therefore, concentrating on the problems of users at the cell edge, we leave the effect of distance is left aside and a selective transmission of the strong interfering users is proposed based on AOA and AOD. Since the interference in Eq.(10) is large when cos(θl′k′l′p′)-cos(φl*l′p)=0 and gradually decreases with the difference |θl′k′l′p′±φl*l′p| increasing, it can simply define user k to be the strong interfering user if
(16)
2.3 Cell grouping
In this section, the effect of interferences from the aspect of the whole systems is analyzed, which has been discussed individually in Section 2.2. Note that considering the effects of interferences in the system as a whole relate to the time assignment of the pilots and data in different cell groups. Therefore, cell grouping is one of the key issues.
For simplicity, the inter-group interference from adjacent cells is concentrated on but the interference from others are ignored, especially the cells relatively nearby in the same group. The problem of this intra-group interference is similar to that in the traditional aligned pilots scheme, which can be thought of as being analogous to frequency reuse that the more groups (larger G) the less intra-group interference. However, compared with inter-group interference, this intra-group interference is dramatically reduced when G≥3 due to larger distances between cells.
Considering the more severe inter-group interference from cell lg′(cell lg′belongs to group g′) to cell lg, using Eq.(16), it is found that users allocated around ±φlglg′q in cell lg′are the main interference source and should be stopped, which are symmetrically distributed with respect to the antenna array. To have less temporally stopped users within a smaller area in cell lg′, the cell lgin group g should be allocated symmetrically with respect to the antenna array of BS lg′and the antenna array in each cell should be perpendicular to the cell edge (see Fig.1 and Fig.3).
Therefore, the selective transmissions during the time-shifted pilots respectively in the case of 3 cell groups and the case of 7 cell groups are shown in Fig.3, where the users in the blue area are temporally stopped while the pilots are transmitted in gray areas.

Fig.3 Cell grouping and the selective transmission
2.4 Channel estimation
The proposed selective transmission strategy with cell grouping reduces the interference to a great extend, but there is still some residual interference, because of the unachievable asymptotic behavior of the interference and unfeasible infinite antenna arrays. This residual interference directly affects the channel estimation and system performance, see the analysis in Section 2.1. Therefore, efficient channel estimations resisting both the interference and noises are required. Obviously, the simplest LS estimation technique used in Ref.[13] is inapplicable. Using additional information like SNR and spatial feature, a covariance-based Bayesian estimation is proposed in Ref.[11]. Here, to fully explore the channel statistics, based on both the time coherence and spatial coherence of the channel, a channel estimation scheme using Kalman filter is proposed.
By vectorizing the received signal and noise, the signal received in Eq.(5) can be rewritten as
(17)
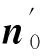

(18)
where

(19)
Since the propagation coefficient αlklp(t) follows the Jakes’ power spectrum of maximum Doppler frequency fd, the variations of hl*k*l*(t) can be well approached by an AR process of order one
hl*k*l*(t)=Ahl*k*l*(t-1)+μ(t)
(20)


(21)
with
Rl*k*l*,1=E{hl*k*l*(t)hl*k*l*(t-1)H}
(22)

The state model Eq.(20) and the observation model Eq.(17) allow us to use Kalman filter to track the channels through two stages:
Time update equations:
Measurement update equations:
ε(t)=[IM-K(t)Sk*]ε′(t)

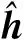

Fig.4 Description of the proposed scheme
3 Simulation results

The proposed scheme (Proposed) is evaluated with 3 cell groups (Proposed (3)) and 7 cell groups (Proposed (7)), respectively. In addition, the performance of the proposed selective transmission using time-shifted pilots and cell grouping but Bayesian estimator (STSP- Bayesian estimation), the generall transmission using time-shifted pilots[13]and Kalman estimation (TSP-Kalman estimation), the transmissions employing aligned pilots (Aligned pilots) and coordinated assignment of aligned pilots (Coordinated aligned pilots)[11]is presented.
Fig.5, Fig.6, Fig.7 and Fig.8 give the performance versus number of antennas at BS with the downlink SNR 12dB and uplink SNR 7dB. Fig.5 shows that both the proposed selective transmission and the coordinated aligned pilots have lower estimation errors than the traditional transmissions using aligned pilots and time-shifted pilots, because of the interference reduction by exploiting the special correlation. Besides, the estimators also play an important role in estimation accuracy that the proposed scheme performs better than STSP-Bayesian estimation. Therefore, the proposed scheme has much more flexibility and provides the lowest estimation error by both the selective interference reduction and effective filtering of interferences based on the time-spacial correlation. Since the correlation is increasing with the increased antennas, the proposed scheme improves quickly with antennas from 10 to 40.

Fig.5 Channel Estimation MSE vs. BS antenna number
Fig.6 shows the average received downlink SINR at user versus the antennas increasing. Obviously, the proposed selective transmissions have higher SINR, because of interference reductions from the stopped strong interfering users. Also the estimation error plays an important role, and therefore the proposed scheme shows better SINR. Moreover, the proposed scheme with 7 cell groups has higher average SINR than the case of 3 cell groups due to long time of stopping users and pilots transmission in adjacent cells.

Fig.6 Downlink SINR vs. BS antenna number

Fig.7 Downlink system throughput vs. BS antenna number
Fig.7 and Fig.8 show the downlink and uplink throughput per cell versus antennas increasing, respectively. The proposed scheme has the higher throughput both in the downlink and uplink due to the interference reducing the filtering, which provides improvement over the loss of the user stop when the antenna size is large. In the comparison between the proposed schemes of 3 cells groups and of 7 cell groups, the 7 cell groups have higher downlink throughput for average downlink SINR but lower uplink throughput for a bit poorer channel estimation.

Fig.8 Uplink system throughput vs. BS antenna number
Fig.9 gives the channel MSE versus uplink SNR with downlink SNR 12dB and M=50 antennas at the BS. Both the proposed schemes and the aligned pilots transmission have little estimation MSE improvement with the SNR from 10dB to 30dB. It demonstrates that the interference is the main factor affecting estimation errors and thus the increase of power cannot provides significant improvements. For this reason, the proposed scheme gets a better performance by effectively reducing interference.

Fig.9 Channel Estimation MSE vs. SNR
4 Conclusions
A scheme of selective transmission using time-shifted pilots with cell grouping is proposed. Based on physical channel models, the behavior of interfering is analyzed. It shows that except for the intra-cell interferences, inter-cell interferences between the pilots and data become the challenges. To cope with these problems, the interference by selecting users to temporally stop transmitting and minimize the stopped users by cell grouping design is reduced. Further, to deal with the inevitably residual interference, the channel estimation using Kalman tracking to filer out both the interference and noise is proposed. The numerical results show that both the proposed transmission and estimation play important roles in the improvement of system performance.
[ 1] Hoydis J, Hosseini K, Brink S t, et al. Making smart use of excess antennas: massive MIMO, small cells, and TDD.BellLabsTechnicalJournal, 2013, 18(2): 5-21
[ 2] Rusek F, Persson D, Lau B K, et al. Scaling up MIMO: opportunities and challenges with very large arrays.IEEESignalProcess, 2013, 30(1): 40-60
[ 3] Jose J, Ashikhmin A, Marzetta T L, et al. Pilot contamination and precoding in multi-cell TDD systems.IEEETransWirelessCommun, 2011, 10(8): 2640-2651
[ 4] Tsai J A, Buehrer R M, Woerner B D. The impact of AOA energy distribution on the spatial fading correlation of linear antenna array. In: Proceedings of the IEEE Vehicular Technology Conference, Birmingham, UK, 2002. 933-937
[ 5] Ngo H Q, Marzetta T L, Larsson E G. Analysis of the pilot contamination effect in very large multicell multiuser MIMO systems for physical channel models. In: Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011. 3464-3467
[ 6] Hoydis J, Brink S t, Debbah M. Massive MIMO in the UL/DL of cellular networks: how many antennas do we need.IEEEJSelAreasCommun, 2013, 31(2): 160-171
[ 7] Ngo H Q, Larsson E G. EVD-based channel estimation in multicell multiuser MIMO systems with very large antenna arrays. In: Proceedings of the IEEE International Conference on Acoustics, Speed and Signal Processing(ICASSP), Kyoto, Japan, 2012. 3249-3252
[ 8] Nguyen S, Ghrayeb A. Compressive sensing-based channel estimation for massive multiuser MIMO systems. In: Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 2013. 2890-2895
[ 9] Cottatellucci L, Muller R R, Vehkapera M. Analysis of pilot decontamination based on power control. In: Proceedings of the IEEE Vehicular Technology Conference (VTC), Dresden, Germany, 2013. 1-5
[10] Muller R R, Vehkapera M, Cottatellucci L. Blind pilot decontamination.IEEEJournalofSelectedTopicsinSignalProcessing, 2013, 8(5): 773-786
[11] Yin H, Gesbert D, Filippou M, et al. A coordinated approach to channel estimation in large-scale multiple-antenna systems.IEEEJournalonSelectedAreasinCommunications, 2013, 31(2): 264-273
[12] Appaiah K, Ashikhmin A, Marzetta T L. Pilot Contamination Reduction in Multi-User TDD Systems. In: Proceedings of the 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 2010. 1-5
[13] Fernandes F, Ashikhmin A, Marzetta T L. Inter-cell interference in noncooperative TDD large scale antenna systems.IEEEJournalonSelectedAreasinCommunications, 2013, 31(2): 192-201
[14] Mahyiddin W A W M, Martin P A, Smith P J. Pilot Contamination Reduction Using Time-Shifted Pilots in Finite Massive MIMO Systems. In: Vehicular Technology Conference (VTC Fall), Vancouver, Canada, 2014. 1-5
[15] Shi J, Xiaoyu W, Zheng L, et al. Zero-forcing beamforming in massive MIMO systems with time-shifted pilots. In: Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 2014. 4801-4806
[16] Sayeed A M. Deconstructing Multiantenna Fading Channels.IEEETransactionsonSignalProcessing, 2002, 50(10): 2563-2579
[17] Zukang S, Runhua C, Andrews J G, et al. Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization.IEEETransactionsonSignalProcessing, 2006, 54(9): 3658-3663
Yang Ruizhe, born in 1982. She received the Ph.D. degree in Signal and Information Processing from Beijing University of Posts and Telecommunications, Beijing, P.R. China, in 2009. Since 2009, she has been with the School of Electronic Information and Control Engineering, Beijing University of Technology, Beijing, P.R. China. Her current research interests are wireless communications, including the resource allocation in OFDM systems, MIMO systems, and the channel estimation.
10.3772/j.issn.1006-6748.2016.01.014
① Supported by the Program for Excellent Talents in Beijing (No.2014000020124G040), National Natural Science Foundation of China (No. 61372089, 61571021) and National Natural Science Foundation of Beijing (No. 4132007, 4132015, 4132019).
② To whom correspondence should be addressed. E-mail: yangruizhe@bjut.edu.cnReceived on Mar. 9, 2015
 High Technology Letters2016年1期
High Technology Letters2016年1期
- High Technology Letters的其它文章
- Time difference based measurement of ultrasonic cavitations in wastewater treatment①
- Research on the adaptive hybrid search tree anti-collision algorithm in RFID system①
- An improved potential field method for mobile robot navigation①
- Robust SLAM using square-root cubature Kalman filter and Huber’s GM-estimator①
- CSMCCVA: Framework of cross-modal semantic mapping based on cognitive computing of visual and auditory sensations①
- Mixing matrix estimation of underdetermined blind source separation based on the linear aggregation characteristic of observation signals①
