Global optimization of manipulator base placementby means of rapidly-exploring random tree①
Zhao Jing (赵 京), Hu Weijian②, Shang Hong, Du Bin
(*College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, P.R.China)(**National Earthquake Response Support Server, Beijing 100049, P.R.China)
Global optimization of manipulator base placement
by means of rapidly-exploring random tree①
Zhao Jing (赵 京)*, Hu Weijian②**, Shang Hong**, Du Bin*
(*College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, P.R.China)(**National Earthquake Response Support Server, Beijing 100049, P.R.China)
Due to the interrelationship between the base placement of the manipulator and its operation object, it is significant to analyze the accessibility and workspace of manipulators for the optimization of their base location. A new method is presented to optimize the base placement of manipulators through motion planning optimization and location optimization in the feasible area for manipulators. Firstly, research problems and contents are outlined. And then the feasible area for the manipulator base installation is discussed. Next, index depended on the joint movements and used to evaluate the kinematic performance of manipulators is defined. Although the mentioned indices in last section are regarded as the cost function of the latter,rapidly-exploring random tree (RRT) and rapidly-exploring random tree*(RRT*) algorithms are analyzed. And then, the proposed optimization method of manipulator base placement is studied by means of simulation research based on kinematic performance criteria. Finally, the conclusions could be proved effective from the simulation results.
base placement, rapidly-exploring random tree (RRT), rapidly-exploring random Tree*(RRT*), optimization
0 Introduction
Because of the interrelationship between the base placement of the manipulator and its operation object, it is significant to analyze the accessibility and workspace of manipulators for the optimization of their base location. Kamrani, et al.[1]proposed a new approach for optimal base placement by using a response surface method on the concept of path translation and rotation. Aly, et al.[2]developed a method for base location optimization of manipulators in a specific workcell, where a genetic algorithm was applied for optimizing solutions in the finite point set generated in the discrete process of the workspace. Bu, et al.[3]presented an analysis of the feasible base area for manipulators based on operation sequence optimization, before that the area is calculated then divided into discrete grids to reduce computation time. Yang, et al.[4]described a numerical computation method of an open-loop manipulator end-effector reaching the base of a specified point. This method is characterized by translating the optimization of the base placement into the solution of the position and orientation of the base with the definition of a fixed reference frame.
To estimate the implementation process of a specific task, performance measures are usually used to evaluate the base location of manipulators. Santos et al.[5]proposed a strategy to work out the optimal task location with power and manipulability being performance evaluation index, considering maximizing the manipulator accuracy and minimizing the mechanical power consumption. Hammond, et al.[6]addressed the use of a multi-objective weighted isotropy measure as a task agility index in optimizing base placement under the condition of a complex, multitask workcell. For heavy-duty manufacturing tasks, a torque-weighted isotropy measure[7]is proposed as the metric for the optimization of the manipulator base. The effectiveness lies in the decrease of energy consumption on the premise of adequate global isotropy. Nektarios, et al.[8]illustrated the approximation of the minimum manipulator velocity ratio(AMMVR) targeted at the optimization of velocity performance in the study on the base location of manipulator end-effector performing a position and orientation path following task of a given 3D curved path and orientation.
At present, a number of algorithms could make motion planning in the joint space, such as A*[9,10]and genetic algorithm[11]. However, with the growth of dimensions, the computational complexity increases sharply and expectant results could not be obtained. And the rapidly-exploring random tree (RRT) algorithm[12]proposed by LaValle could find out the feasible solution quickly to solve the path planning problems in higher joint space, which is much better than the traditional methods. But, the optimal solution of joint movements have not carried out by this algorithm because there are redundant joint movements for a given end-effectors path. Even though many scholars have tried to induce the growth of the searching tree by generating nodes[13], optimizing paths[14]and defining index[15], as the algorithm itself fails to introduce the known information of the configuration nodes into the expansion of the next to calculate a certain target function between all candidate nodes and the impact point, the paths obtained is unlikely to be the optimum. Karaman et al.[16]proposed the rapidly-exploring random tree*(RRT*) algorithm on the basis of existing searching algorithm, which could make a redesign of the RRT expansion by adopting an incremental sampling-based technique to obtain an asymptotic optimal characteristic, which also could provide a guarantee of convergence to optimal solutions.
1 Problem description
In current study, mostly only the candidate base placement in the feasible area of base (FAB) is evaluated regardless of the quality of the implementing task. In fact, base placement optimization of manipulators should consider two factors: 1) the quality of manipulators performing a given task in a specific base placement; 2) global optimization of base placement in FAB.
1.1 Optimal motion planning
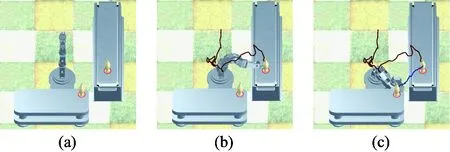
A manipulator is installed at arbitrary point Bjon the ground in the workcell as shown in Fig.1. The manipulator is placed vertically with its end-effector point being at PEin the initial state. End-effector point PSand point PTcorrespond to initial configure xinitand goal configure xgoalof the manipulator, respectively. The task which the manipulator must do is that the manipulator picks the bottle at point PS, and places it at point PT. During the process of completing the specific task, the RRT algorithm is employed to carry out the motion planning from point PEto point PS. Moreover, the RRT*algorithm could be applied in the motion planning for the manipulator moving from PSto PTwith index imposing constraints, thus to obtain the optimal path satisfying the limitations. Cost function c(·) is used to evaluate the path and the joint movements, the result of which will be the scores of manipulator base at Bj.

Fig.1 Description of the pick-and-place operation
1.2 Base placement optimization
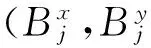
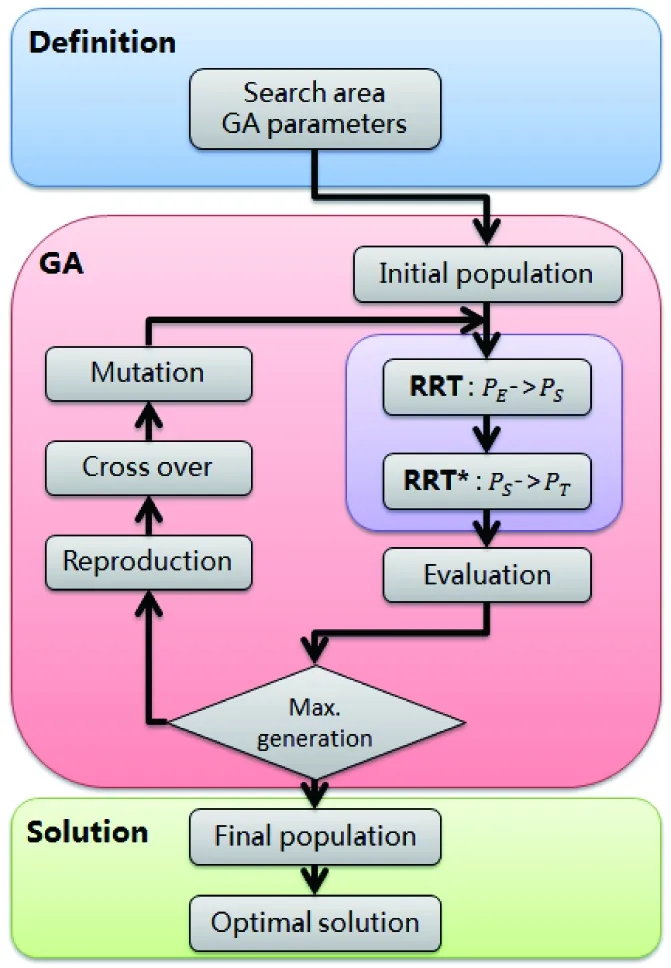
Fig.2 Flowchart of the base placement optimization process
2 Analysis of FAB
The feasible area of base is codetermined by three factors: workspace of the manipulator, position of the manipulation target and obstacles in the workcell. As for a spatial manipulator, It is supposed that without consideration of joint limits, its workspace is a solid sphere with a radius of R. The manipulator base locates in the center of the sphere, as showed in Fig.3. Move the sphere to reach a tangency with target point Pi. The horizontal plane with Piis tangent to the sphere and gets a circle of radius RT, where RTdenotes the maximum radius of FAB to specific point Pi, which is given by
(1)
whereRis the radius of the manipulator workspace, hPis the height of the point Pirelative to the ground, and hBis the height of the manipulator base relative to the ground.
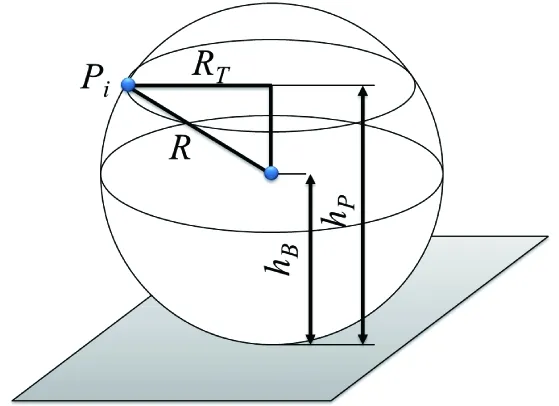
Fig.3 Determination of FAB of the given point

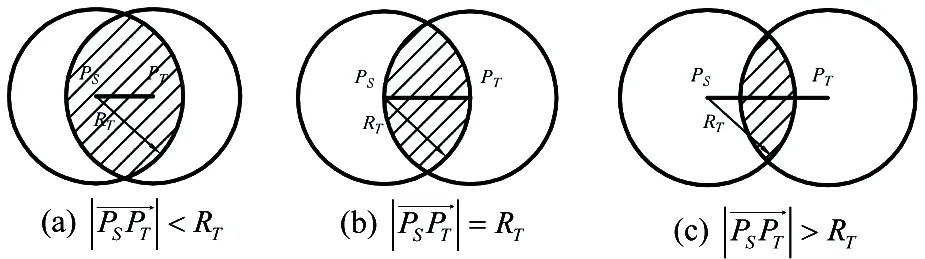
Fig.4 FAB of the manipulator when the end-effector moves along a path
In fact, there are other factors that can possibly influence base placement of manipulators. For example, installment of manipulators cannot interfere with operating platform. Joint movements of manipulators cannot collide with possible obstacles. The height of the target object relative to the ground directly determines the size of FAB of the specific point. At the same time, singular configurations during task implementation should be avoided.
3 Mean manipulation capability
In order to evaluate the kinematics dexterity quantitatively, Yoshikawa[17]defined the manipulability index as
(2)
Let wi(i=1,…,n) denote the manipulation capability corresponding to path points Pi(i=1,…,n) of manipulator end-effector, the total manipulation capability of the task implementation will be
(3)
In order to make path manipulability obtained from different base location comparable, the mean manipulation capability (MMC) index is defined as
(4)
4 An improved RRT*
The RRT*algorithm makes a redesign of the RRT expansion by adopting an incremental sampling-based technique to obtain an asymptotic optimal characteristic, which provides guarantee of convergence to optimal solutions. The main feature is that the known information of the configuration nodes is introduced into the expansion of the next to calculate a certain objective function between all candidate nodes and the target point. It is seen as the index to decide if the candidate node belongs to optimal path nodes, thus to choose one with the optimal objective function to be the next path node. Index defined in the above section is used as cost function to limit the expansion of tree nodes in the RRT*algorithm to reach the optimal joint movements of manipulators under constraint conditions.
Let the motion planning for manipulators obtain the minimum cost function an example. In the algorithm, a new node and near by nodes could be evaluated instead of being directly added to the node tree, which is divided into two steps:
Step 1: Near configurations set is generated on the basis of a new configuration.
For an arbitrary joint configuration xnewand a finite set V⊂X of near configurations, Near(x) procedure returns the set of all x∈V that are close to xnew. The relationship between xnewand x can be expressed as
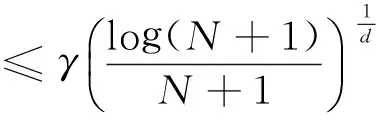
(5)
where γ is a constant, N is the number of joint configurations in search tree, and d is the dimensions of joint space.
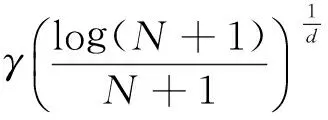
Step 2: Father and child nodes of the new node are searched in near configurations.
The essence of the search for father and child nodes in the set V is to go through the whole V to find a node xnearthat minimizes the cost function from the initial xinitto the goal xnew. The calculation criterion for searching father and child nodes are respectively represented as
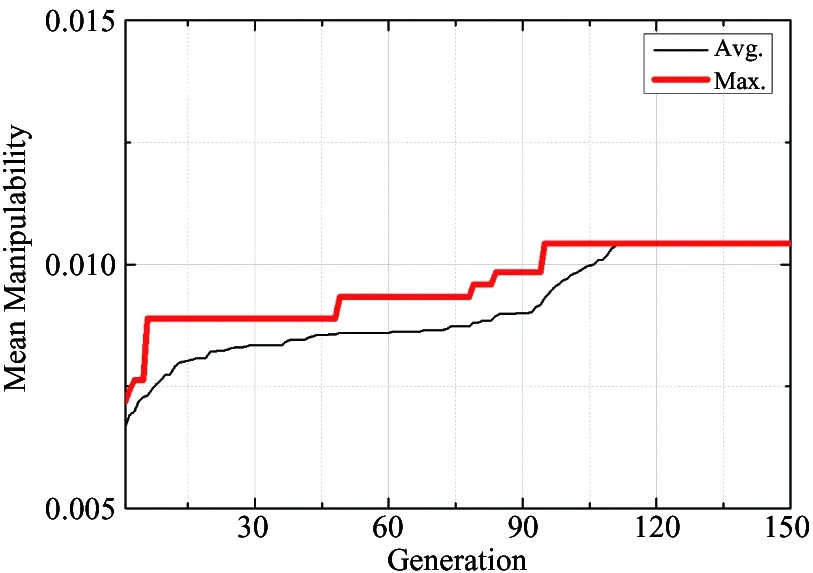
Cost(xnear)+c(xnear,xnew) (6) Cost(xnew)+c(xnear,xnew) (7) Where Cost(x′) is the total cost from initial node xinitto current node x′. c(xnear,xnew) represents the cost from xnearto xnew. To obtain the motion planning of manipulators by the algorithm above provides not only a guarantee of high efficiency in solving, but also optimization of manipulator joint movements. In the case of the same task implemented and the same initial state of manipulators, the shortest distance of manipulator end-effector as cost function for RRT*algorithm is taken. The solutions of motion planning for manipulators using RRT and RRT*are shown in Fig.5, which illustrates that compared with RRT, path length searched by RRT*has been shortened to a large extent and is approximate to the shortest one. Fig.5 Comparison of the motion planning for the same task by RRT and RRT* 5.1 Simulation object and environment Fig.6 Coordinate frames of the manipulator The maximum radius of FAB of a specific target point is figured out as RT=0.4305m by equation . According to analyses above, FAB of the pick-and-place operation is illustrated in the oblique line area in Fig.7. Choose the search area of the base, which is marked as the green rectangle area in Fig.7 within the coordinate rage of x=[0.46448, 0.65938]m, y=[0.53216, 0.69]m, in order to make it easier for the calculator program to work out the base placement, as well as to take the installment boundary of the manipulator into consideration. As the radius of the manipulator workspace mentioned in this paper is kind of smaller, the area of FAB is relatively smaller, too. Fig.7 Descriptions of FAB and the search area in GA 5.2 Optimization simulation Let MMC during the implementation of a specific task be the optimization objective, in other words, to obtain the maximum MMC. The fitness function can be defined by (8) wherekis thekthchromosome in a generation. The size of the initial population generated randomly is 18 and the number of reproduction generation is 150. Each gene on the chromosome is encoded in 32-bit binary encoding with crossover probability being 0.75 and mutation being 0.10. The elite reserved strategy is adopted in the selection of chromosome. The positional accuracy of the RRT*algorithm reaching the target point is e=10-3m. The evolution process of the genetic algorithm is shown in Fig.8, where the thick line represents the converging conditions of the minimum joint total displacement and the thin denotes the average joint total displacement of population in each generation. It illustrates that the optimal solutions can be obtained as the algorithm implemented to the 94thgeneration, that is, there is no better solution in later iterative process and algorithmic convergence is to stabilize. The average of the joint total displacement shortens with the increase of search iterations and its convergence is tending to the value of the minimum joint total displacement. On the basis of the chromosome and its fitness function, the distribution of the joint total displacement in different locations in FAB is shown in Fig.9, which displays that the coordinate of the optimal base location is (0.5113, 0.5525)m and MMC will be 0.0104. The movement during the task implementation of the manipulator at this point is shown in Fig.10. Fig.8 Evolutions of the average and maximum solution for MMC Fig.9 Distribution of MMC in the search area Fig.10 Movements with the strongest MMC of the manipulator A new optimization method of manipulator base placement are proposed in this paper. Compared to the traditional methods, the method in this study takes the influence of the motion planning on placement optimization into consideration. The planning process for the task by manipulators is accomplished to achieve optimal kinematic performance in every task, then to perform genetic algorithm in FAB of the manipulator to obtain the optimal base location. From the simulation results, optimization algorithm of manipulator base location based on kinematic performance criteria could be proved effective. According to the task of the manipulator end-effectors, to obtain the feasible area of the base location through analyzing the workspace of manipulators and obstacles in the workcell is a good way to facilitate the optimization solution. However, for the research complicated movement of the end-effector such as complex 3D curve of space, the analysis method of FAB should be improved. The simulation results show that the RRT*algorithm could obtain the optimal path by optimizing the path during the process of searching. Because the searching tree may be degenerated into RRT for limited optimization capability with an undersized γ and an oversized γ could cause this capability too high to search out enough path nodes for the use of practical controls has a great impact on the growth of RRT*. In future research, a dynamic index will be introduced into the RRT*algorithm. And this optimal method will also be applied to rescue robots. [ 1] Kamrani B, Berbyuk V, Wäppling D, et al. Optimal robot placement using response surface method.TheInternationalJournalofAdvancedManufacturingTechnology, 2009, 44(1-2): 201-210 [ 2] Aly M F, Abbas A T, Megahed S M. Robot workspace estimation and base placement optimisation techniques for the conversion of conventional work cells into autonomous flexible manufacturing systems.InternationalJournalofComputerIntegratedManufacturing, 2010, 23(12): 1133-1148 [ 3] Bu W H, Liu Z Y, Tan J R. Industrial robot layout based on operation sequence optimisation.InternationalJournalofProductionResearch, 2009, 47(15): 4125-4145 [ 4] Yang J J, Yu W, Kim J, et al. On the placement of open-loop robotic manipulators for reachability.MechanismandMachineTheory, 2009, 44(4): 671-684 [ 5] Santos R, Steffen V, Saramago S. Optimal task placement of a serial robot manipulator for manipulability and mechanical power optimization.IntelligentInformationManagement, 2010, 9(2): 512-525 [ 6] Hammond Iii F L, Shimada K. Improvement of redundant manipulator task agility using multiobjective weighted isotropy-based placement optimization. In: 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO 2009), Guilin, China, 2009. 645-652 [ 7] Hammond Iii F L, Shimada K. Improvement of kinematically redundant manipulator design and placement using torque-weighted isotropy measures. In: 2009 International Conference on Advanced Robotics (ICAR 2009), Munich, Germany, 2009. 1-8 [ 8] Nektarios A, Aspragathos N A. Optimal location of a general position and orientation end-effector’s path relative to manipulator's base, considering velocity performance.RoboticsandComputer-IntegratedManufacturing, 2010, 26(2): 162-173 [ 9] Sun L W, Yeung C K. Port placement and pose selection of the Da Vinci surgical system for collision-free intervention based on performance optimization. In: 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2007), San Diego, USA, 2007. 1951-1956 [10] Jia Q, Chen G, Sun H, et al. Path planning for space manipulator to avoid obstacle based on A* algorithm.JixieGongchengXuebao/JournalofMechanicalEngineering, 2010, 46(13): 109-115 [11] He G Z, Gao H M, Zhang G, et al. Using adaptive genetic algorithm to the placement of serial robot manipulator. In: IEEE International Conference on Engineering of Intelligent Systems (ICEIS 2006), Islamabad, Pakistan, 2006. 1-6 [12] Lavalle S M. Rapidly-exploring random trees: a new tool for path planning[R]. Computer science Department, Iowa State University, 1998 [13] Bertram D, Kuffner J, Dillmann R, et al. An integrated approach to inverse kinematics and path planning for redundant manipulators. In: 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, USA, 2006. 1874-1879 [14] Scheurer C, Zimmermann U E. Path planning method for palletizing tasks using workspace cell decomposition. In: 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 2011. 1-4 [15] Du B, Zhao J, Song C. Optimal base placement and motion planning for mobile manipulators. In: ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (IDETC/CIE2012), Chicago, USA, 2012. 1-8 [16] Karaman S, Frazzoli E. Sampling-based algorithms for optimal motion planning.InternationalJournalofRoboticsResearch, 2011, 30(7): 846-894 [17] Yoshikawa T. Manipulability of robotic mechanisms. In: Robotics Research, The Second International Symposium, Kyoto, Japan, 1985. 439-446 Zhao Jing, born in 1961. He received his PhD degree from Beijing University of Technology in 1998. He is currently a professor in College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, China. His research interests include mechanism as well as robotic kinematics and dynamics. 10.3772/j.issn.1006-6748.2016.01.004 ① Supported by the National Science and Technology Support Program of China (No. 2013BAK03B01). ② To whom correspondence should be addressed. E-mail: huweijian.2008@163.comReceived on Dec. 1, 2014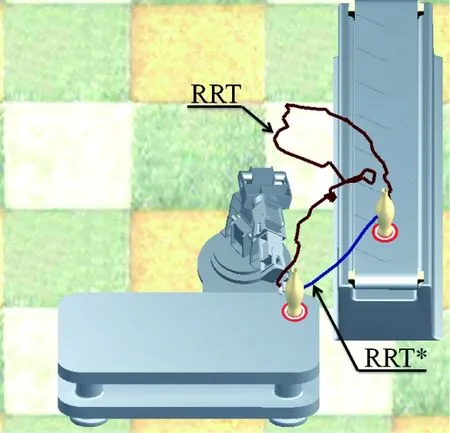
5 Case study




6 Conclusions
 High Technology Letters2016年1期
High Technology Letters2016年1期
