分数阶椭圆型算子系统在非主特征值处近共振的多重解
姚 娟
( 铜仁学院 大数据学院,贵州 铜仁 554300 )
分数阶椭圆型算子系统在非主特征值处近共振的多重解
姚 娟
( 铜仁学院 大数据学院,贵州 铜仁 554300 )
研究分数阶椭圆型系统特征值的性质,对Sobolev空间进行直和分解,并利用临界点理论中的环绕定理和局部鞍点定理,得到了分数阶椭圆型算子系统在非主特征值处近共振的多重解存在性的结论。
分数阶椭圆型系统; 环绕定理; 局部鞍点定理; 近共振; 多重解
1.引言
考虑分数阶椭圆型算子系统

其中Ω⊂Rn(n ≥1)有界开区域,且具有局部Lipschitz边界∂Ω;是位势函数F关于(u, v)∈R2的梯度;λ是一个正的参数。
Lku定义如下:
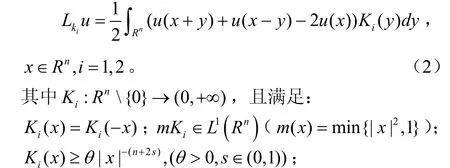
关于系统近共振情况已有很多学者研究,2010年,Suo和Tang在文献[5]中利用环绕定理与局部鞍点定理,得到了合作椭圆系统近共振问题的四个存在性结果;2011年Ke和Tang在文献[6]中利用Landesman-Lazer类型条件、环绕定理以及局部鞍点定理,获得了渐近线性非合作椭圆系统方程在任意高阶特征值附近解的多重性结果;2014年,An 和Suo在文献[7]中利用Ekeland变分原理、山路引理以及鞍点定理,获得了准线性退化椭圆系统方程近共振问题的多重解。本文受到文献[3,5]的启发,通过对分数阶椭圆型算子系统特征值的讨论,研究分数阶椭圆型算子系统在非主特征值处近共振的多重解存在性的结论,丰富和推广了已有文献的相关结论。
2.预备知识
设Xi是一个Rn到Rn的Lebesgue可测函数空间,Xi中任意函数都属于L2(Ω),且映射

属于L2( R2n(CΩ×CΩ),dxdy),CΩ=RnΩ,i=1,2。记Hi={g∈Xi:g=0,a.e.于RnΩ}(i =1,2),其上的
范数定义为:
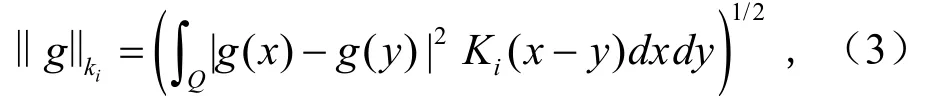
对应内积为:
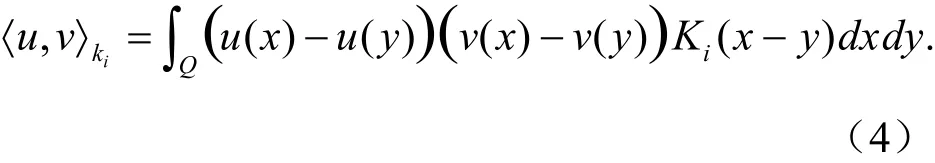
由文献[4]知,Hi为Hilbert空间。记H=H1×H2,定义范数

则H也为Hilbert空间,其中内积为:

z∈H有

记Lz=(LK1u,LK2v),σ(-Δ(L))为问题(1)的特征值集合。根据文献[2]知其特征值具有特性:0<λ1<λ2<…<λk<…,且λ1是正的、单重的和孤立的, 其特征函数(μ ,ν)∈H在Ω上是严格正的函数,并且‖(μ ,ν‖)=1。记Ek为对应特征值λk的特征子空间, Vk=E1⊕E2⊕…⊕Ek为第一个特征值到第k个特征值对应的特征子空间的直和,由特征子空间性质可将H分解为。根据空间的分解和特征值的性质, 可得如下不等式:
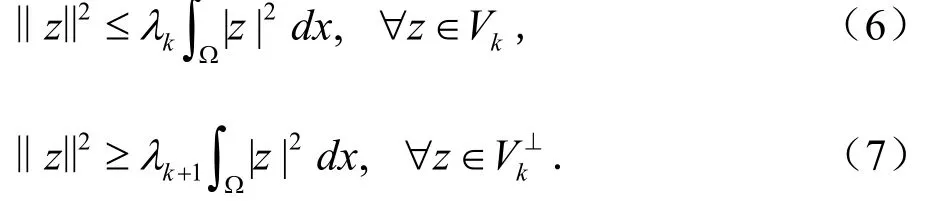
引理2.1(环绕定理[1])若H为Hilbert空间,J∈C1( H, R)且满足(P. S.)条件。若S是空间H的一个闭子集,Q⊂H具有边界∂Q,假设S与∂Q环绕,并且
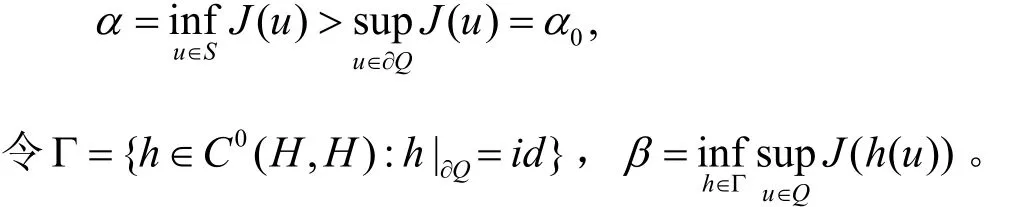
那么,β是J是的一个临界值并且β≥α。
引理2.2(局部鞍点定理[1])假设H=X1⊕X2是Hilbert空间,且dimX1<∞。如果J∈C1( H, R)满足(P. S.)条件,以及对任意的ρ1,ρ2>0,都有

那么存在u0∈H,有J( u0)∈[a, b]且J′( u0)=0,其中

3.本文主要结果
定义泛函I: H→R如下:

因为非线性项F是次线性增长, 通过标准的证明可知,泛函I∈C1( H, R),且z∈H是系统(1)的弱解当且仅当z是泛函I的临界点。记



假设非线性项F满足(A1)及对所有x∈Ω有∇F( x,0)=0。通过估计式(9),Hölder不等式和Sobolev嵌入不等式(6),对所有z∈H可得如下不等式:

以及对所有z, w∈H,有不等式估计:
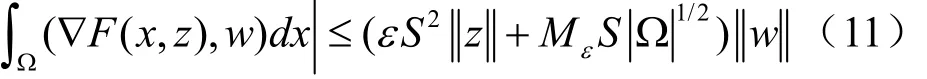
其中S是Sobolev嵌入不等式(5)的最佳常数。
现给出本文的主要结论:
定理3.1 设λk∈σ(-Δ(L))(k≥2)是第k个特征值,假设F满足以下条件:

则存在δ1>0,使得对问题(1)至少有两个解。
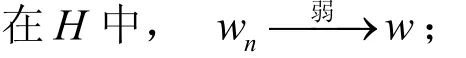

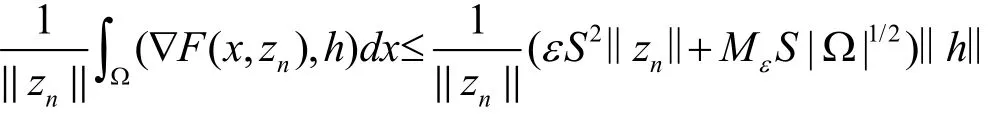
再由ε的任意性,可得,

由(10)同理可证,

通过(12)和(13),可得

其中,

从而得
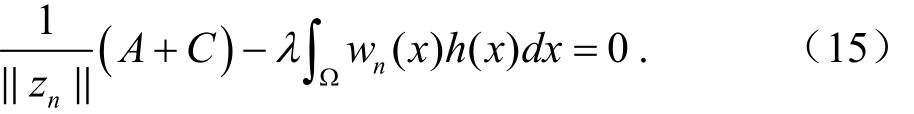
故有,

另外,由(12)和(14)可得

进而得,

(II)应用引理2.2得到泛函I第一个临界点。
首先,当条件(A1)与(A2)满足时,存在δ1>0,当λ∈(λk, λk+δ1)时,存在常数G1, K1, F以及ξ>0,使得
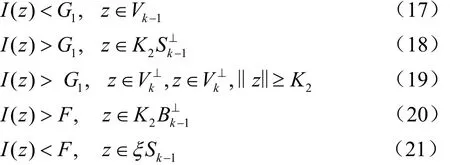


分小时这个性质独立于λ的取值。
现证(18)式。由F的条件和性质可知,存在常数
则根据(6)式及G的性质有
星光村位于罗江区鄢家镇北缘,辖区面积2.65平方公里,辖10个村民小组,500户,1479人。全村以蜜柚为主的水果种植面积接近2500亩。2017年全村人均纯收入达15385元。2016年,当地政府凭借星光村优越的基础条件,将其作为旅游开发示范点纳入鄢家镇岭上花开农业公园景区进行整体规划设计和开发。

因为ϕ∈Ek,Ek是有限维子空间,且函数G是强制的,根据条件(A1)与(A2)式可得

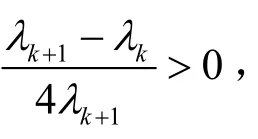

那么由引理2.2得到泛函I的第一个临界点,记作w1,其对应的临界值d1≤G1。
(III) 利用引理2.1获得泛函I的第二个临界点。一方面,对和任意的,根据(7)、(8)和(10)



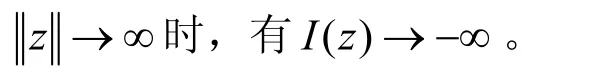
故对(II)中给出的K2,存在足够大的1K2θ>,使对∀z∈θ1Sk,都有I( z)<G2。记

因为θ1Sk和Vk⊥环绕,由引理2.1得到泛函I第二临界点,记为w2,且对应到的临界值为:
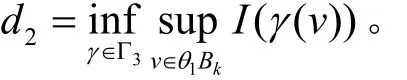
(IV)证明以上得到的两个解w1与w2是不同的。对任意映射γ∈Γ3,因为θ1>K2,故有:γ的像要么与相交,要么存在,且。这就由估计式(18)和(19)推出因此d2>G1≥d1。
[1] Rabinowitz P H. Minimax methods in critical point theory with applications to differential equations[M]. Published for the Conference Board of the Mathematical Sciences by the American Mathematical Society, 1986.
[2] Gilbarg D, Trudinger N S. Elliptic partial differential equations of second order[M]. Springer-Verlag, 1983.
[3] Paiva F O, Massa E. Semilinear elliptic problems near resonance with a nonprincipal eigenvalue[J]. J Math Anal Appl, 2008, 342: 638-650.
[4] R. Servadei and E. Valdinoci. Mountain pass solutions for non-local elliptic operators[J]. J. Math. Anal. Appl, 2012, 389( 2): 887-898.
[5] Suo H M, Tang C L. Multiplicity results for some elliptic systems near resonance with a nonprincipal eigenvalue[J]. Nonlinear Analysis, 2010, 73: 1909-1920.
[6] Ke X F, Tang C L. Existence and multiplicity of solutions for asymptotically linear noncooperative elliptic systems[J]. Math Anal Appl, 2011 375(2): 631-647.
[7] An Y C,Lu X, Suo H M.Existence and multiplicity results for a degenerate quasilinear elliptic system near resonance[J]. Boundary Value Problems, 2014: 184.
[8] massa E,Rossato R A. Multiple solutions for an elliptic system near resonance[J]. Math Anal Appl, 2014, 420: 1228-1250.
[9] Xia Aliang , Yang Jianfu. Regularity of nonlinear equations for fractional Laplacian[J]. Proceedings of the American Mathematical Society 2013, S0002-9939: 11734-X.
Multiplicity results for some fractional elliptic type systems near resonance with a nonprincipal eigenvalue
Yao Juan
( School of Data Sciences, Tongren University, Tongren, Guizhou 554300, China )
The fractional elliptic type systems are studied. According to the chareteristics of the eigenvalues for a class of fractional elliptic type systems, the Sobolev space is resolved ;Some multiplicity results of solutions are obtained for a class of fractional elliptic type systems near resonance with a nonprincipal eigenvalues by classical link theorem and a local saddle point theorem in critical theory.
fractional elliptic type systems, link theorem, local saddle point theorem, near resonance, multiplicity solutions
O175.25
A
1673-9639 (2016) 04-0163-05
(责任编辑 毛 志)(责任校对 印有家)
2016-03-24
贵州省科技合作计划项目(黔科合LH字[2015]7247号)。
姚 娟(1989-),女,贵州铜仁人,硕士,研究方向:非线性泛函分析。

