基于贝叶斯公式的河流水质综合评价——以铜仁市锦江河为例

毛 志，陈亚丽

（ 铜仁学院 大数据学院，贵州 铜仁 554300 ）

基于贝叶斯公式的河流水质综合评价
——以铜仁市锦江河为例

毛 志，陈亚丽

（ 铜仁学院 大数据学院，贵州 铜仁 554300 ）

以《地表水环境质量标准》（GB3838-2002）为评价标准，选取10个水质评价指标，根据铜仁市锦江河13个监测断面多年的水质监测数据平均值，利用贝叶斯公式对铜仁市锦江河进行水质评价。通过评价结果可以看出在多年平均情况下除锦江东门桥下断面符合Ⅲ类标准外，其余12个断面水质均优于规定的Ⅲ类标准，符合Ⅱ类水质标准。

贝叶斯公式； 河流水质评价； 锦江河

水是生命之源，人们日常生活用水很多是通过河流中的水净化而来。锦江河是铜仁市碧江区最大河流，全流域面积为4157平方公里，境内4069平方公里，境外湖南省88平方公里，东至辰溪县城郊入沅江，经洞庭湖后汇入长江，是长江上游河流的上游支流[1]。因此，其水质是非常重要的，于是寻找出一种简便、有效的评价锦江河水质的方法成为一项十分迫切而且具有重要意义的工作[2]。由于在水质评价中的不确定因素较多，所以在水质管理中，水环境的不确定性是一个难题。近些年，贝叶斯统计方法越来越多地应用到水环境不确定性问题研究中，其优势在于将水环境的不确定性问题转化成对模型参数的估计量，建立不确定性和估计概率之间的关联，以联合后验分布的数值代表不确定事件发生的概率大小，根据估计概率的大小，决策者可以对不确定性问题进行评估和判断，从而有针对性地开展水质管理工作，提高水质管理的准确度和有效性。本论文旨在通过贝叶斯公式对铜仁市锦江河的水质进行综合评价，同时给水务和环保等部门的管理和决策提供科学参考。

1.数据采集

根据不同的用水要求，我国已制定颁布了不同的水资源质量评价标准，本研究采用《地表水环境质量标准》（GB3838-2002）[3]。结合水质质量评价选择内容和实际监测数据情况，我们选用总氮、化学需氧量、高锰酸盐指数、五日生化需氧量、氨氮、总磷、挥发酚、汞、砷、铅共10个水质评价指标[4]。

监测站点的布设在总体和宏观上必须能反映出水系或所在区域的水环境质量状况[5]。各监测站点的具体位置要能反映所在区域环境的污染特征，要尽可能以最少的监测站点获取最有足够代表性的环境信息，而且还要考虑实际采样时的可行性和方便性。因此监测站点选取的位置应避开死水区、回水区、排污口处，选择顺直河段、河床稳定、水流平稳或水面宽阔、无急流、无浅滩处[6]。综合以上的条件，我们把本文所研究的锦江河分为大江段、小江段和锦江段，选取了13个监测站点（如图1所示），各监测站点的地名及其编号见表1。通过铜仁市环保局，获得各监测站点水质监测指标的多年平均值，

其中化学需氧量、氨氮、高锰酸盐指数的测量值是2008年至2014年内的平均值[7]，其他的水质监测指标测量值是2010年至2014年内的平均值。

图1 锦江河水质监测断面示意图

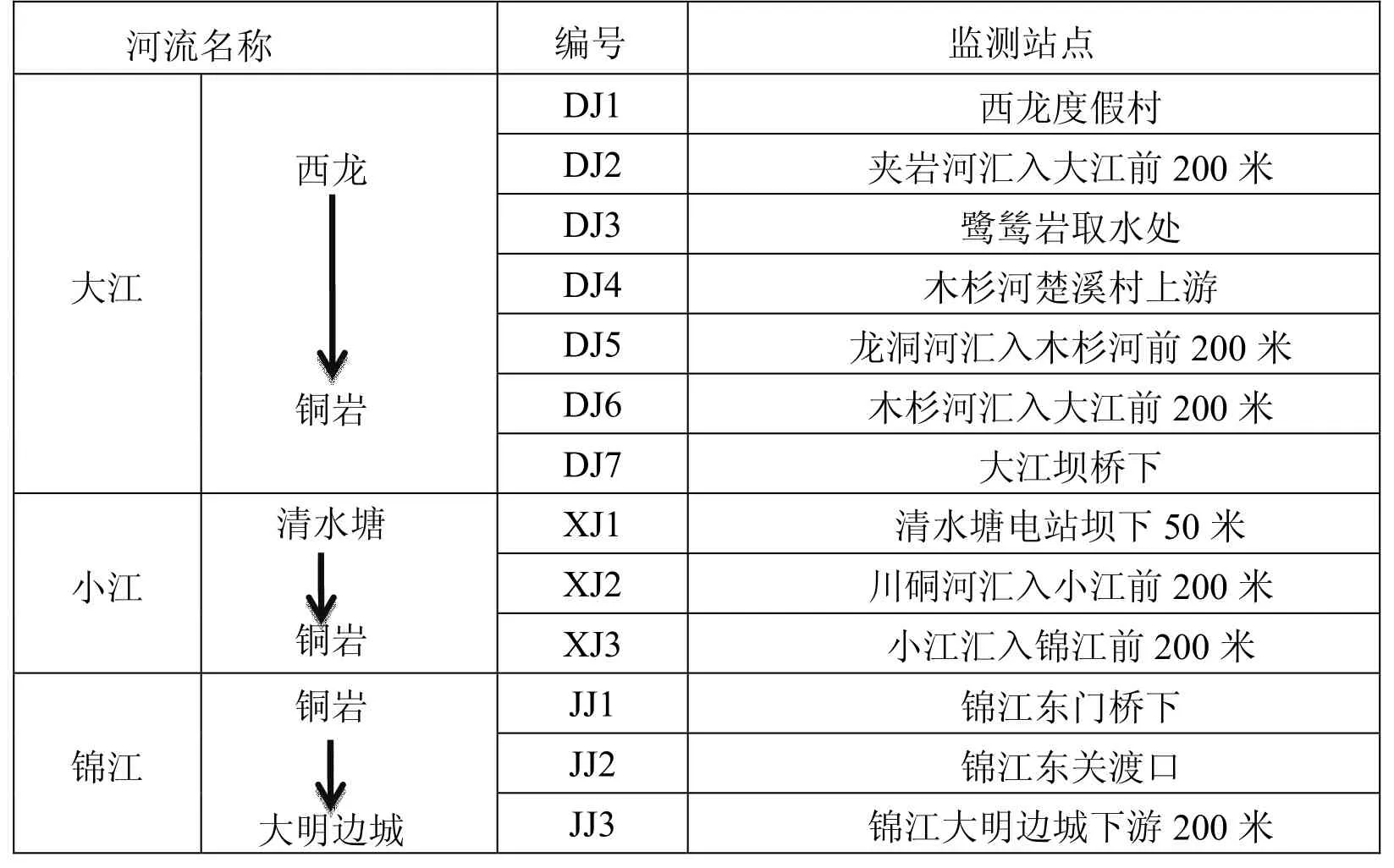
表1 各监测站点的地名及其编号

2.地表水水质评价的贝叶斯模型及方法

2.1.地表水水质评价的贝叶斯模型

根据水质评价的情况，贝叶斯公式可改写为：

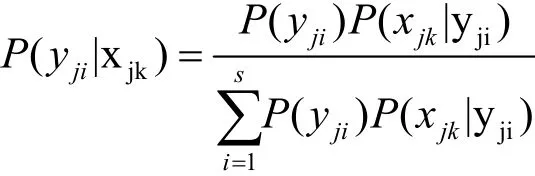
式中yji表示水质类型Bi的值，即水质级别为i的j指标的标准值，xjk表示站点k的j指标的测量值，i为水质级别，j为指标，k为代表站点，在本论文中上式即为铜仁市碧江区锦江河水质评价依据的贝叶斯模型。

2.2.地表水水质评价的贝叶斯方法

（1）计算P( yji)。在没有任何水质信息的条件下，某站点的水质属于某水质级别最为人们接受的

原则是概率相等，即先验概率取

（2）P( xjk|yji)采用几何概率中的距离法计算。以代表站点指标与水质类型标准之间的距离绝对值的倒数进行计算[8]，即

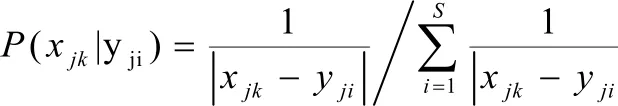
式中j=1,2,···,10，i=1,2,···,5，k=1,2,···,13。如果代表站点的xji距yji越远，则代表站点k的水质级别属于i的可能性就越小。

（3）多指标下综合水质后验概率的求解如下：

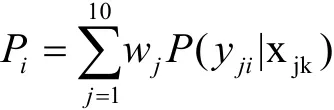
式中wj为不同水质指标的权重，因本文是综合研究，所以就采用等权重[9]，即w1=w2=···=w10=1/10，Pi是综合考虑了10个水质指标信息后代表站点的水质级别为i的概率。

（4）最终的级别h是以最大概率原则决定，即

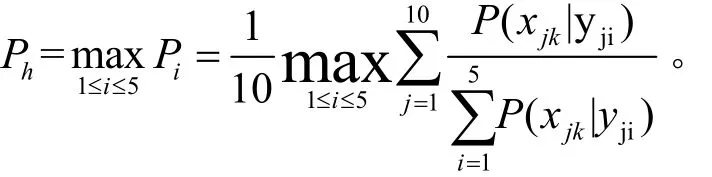
3.基于贝叶斯模型的锦江河河流水质评价

根据水质监测站点的区域分布和监测资料，本文选取10个水质指标，利用铜仁市锦江河13个监测站点多年的水质监测数据平均值[10]，以《地表水环境质量标准》（GB3838-2002）作为标准，通过上述步骤进行计算，得到P( xjk|yji)及Pi值，Pi的值见表2（Pi保留三位小数）。由以上的各个站点Pi的值根据步骤(4)以概率最大原则取五个Pi的最大值（Ph）可以得到13个监测站点的水质级别（见表3）[11]。

4.结论与建议

根据《地表水环境质量评价办法》（GB3838-2002）要求，通过贝叶斯水质评价模型，计算结果表明铜仁市锦江河的13个代表站点多年来的平均水质评价结果为Ⅱ类、Ⅲ类，没有Ⅰ类、Ⅳ类和Ⅴ类水质。在锦江河的13个监测站点中，除锦江东门桥下属于Ⅲ类水质外，其余各监测断面都属于Ⅱ类水质标准。整体来说，锦江河的水质达标，且通过锦江东门桥旁边的污水处理厂的处理后，锦江东关码头和大明边城下游的水质有所改善。但通过计算发现大江的木杉河楚溪村上游、龙洞河汇入木杉河前200米、木杉河汇入大江前200米和大江坪桥下的水质指标中总氮含量接近Ⅳ、Ⅴ类的总氮标准值的概率较大，而且锦江的三个监测站点的总氮接近Ⅳ类的总氮标准值的概率非常大。

表2 各监测站点的不同水质级别的概率

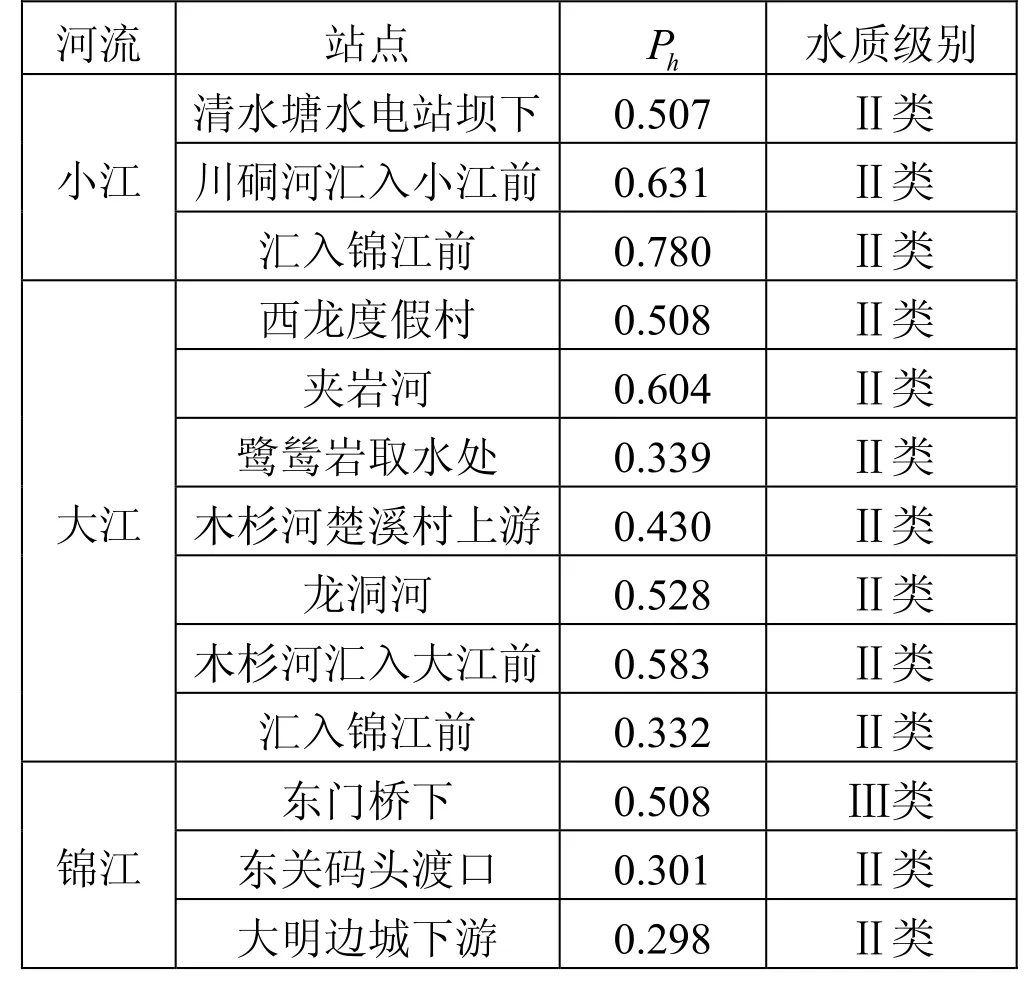
表3 各监测站点水质级别的最大概率hP的值及相应的水质级别

通过贝叶斯公式对锦江河的水质得出的评价结果表明锦江河的河水符合地表水水质标准，但还应加强水质的检测，特别注意保护东门桥下的河水。此外，大江的木杉河楚溪村上游、龙洞河汇入木杉河前200米、木杉河汇入大江前200米和大江坪桥下和锦江监测断面的总氮含量偏高，建议拒绝污染重、耗能高、耗水大的项目进入该区域。通过锦江东门桥旁边的污水处理厂的处理后，锦江东关码头和大明边城下游的水质有所改善。可见，污水处理厂的建设是非常有必要的，应加快污水处理厂的建设及垃圾处置设施建设。

[1] 夏鹏章.长江志·水系篇编撰记述[J].长江志季刊，2003，（2）：41-45.

[2] MO Angelidis, G Kamizoulis. A Rapid Decision-Making Method for the Evaluationof Pollution-Sensitive Coastal Areas in the Mediterranean Sea[J]. Environmental Management, 2005, 35 (6): 811-820.

[3] 齐培培.基于贝叶斯网络的水质污染评价及预测[D].武汉：武汉大学，2009.

[4] 李贵宝，郝红，张燕.我国水环境质量标准的发展[J].水利技术监督，2003，（3）.

[5] 刘红亮.浅谈水环境监测的质量保证与质量控制[J].水文，2012，（10）：320-320.

[6] 李德荣，刘鹤.关于全概率公式和贝叶斯公式的一种新讲解[J].内蒙古统计，2009，18（6）：514-517.

[7] RM Singh, B Datta. Artificial neural network modeling for identification of unknown pollution sources in groundwater with partially missing concentration observation data[J]. Water Resources Management, 2007, 21(3): 557-572.

[8] GF Cooper, E Herskovits. A Bayesian Method for the Induction of Probabilistic Networks from Data[J]. Machine Learning, 1992, 9 (4): 309-347.

[9] 何镇邦，李桂荣.概率论与数理统计[M].北京：北京理工大学出版社，1998.

[10] 郭敬辉.川西滇北地区水文地理[M].北京：科学出版社，1985.

[11] 赵英，郭亮.贝叶斯方法的污染源季节性排放量控制和管理[J].哈尔滨工业大学学报，2014，46（12）：26-32.

The Comprehensive Assessment of Water Quality Based on Bayesian Formula—Taking Jinjiang River as an Example

Mao Zhi, Chen Yali
( School of Data Sciences, Tongren University, Tongren, Guizhou 411105, China )

In this paper, with Standard GB3838-2002 as the evaluation criteria, we select 10 water quality evaluation index，and use the Bayesian formula to assess the water quality of Jinjiang river according to the mean of monitoring data in 13 monitoring sections. The evaluation result shows that the East Gate Bridge section meets Ⅲ class water quality standard and the remaining 12 section water quality get toⅡclass standard.

Bayesian formula, river water quality assessment, Jinjiang river

O211；X824

A

1673-9639 (2016) 04-0150-04

（责任编辑 佘彦超）（责任校对 印有家）

2016-05-10

贵州省普通高等学校创新人才团队项目（黔教合人才团队字[2015]64）。

毛 志（1982-），男，湖南汨罗人，副教授，博士，研究方向：微分方程数值计算，生物信息学。陈亚丽（1991-），女，贵州德江人，铜仁学院数学科学学院2012级数学与应用数学（2）班学生。