邻井干扰条件下的多井压力恢复试井分析方法

孙 贺 东

中国石油勘探开发研究院廊坊分院

邻井干扰条件下的多井压力恢复试井分析方法

孙 贺 东

中国石油勘探开发研究院廊坊分院

孙贺东. 邻井干扰条件下的多井压力恢复试井分析方法. 天然气工业，2016,36(5):62-68.

储层渗透性高、井间连通性较好的气藏，其本质是一个多井系统，气藏投产后，测试井的压力恢复资料容易受邻井的影响，压力导数曲线在中晚期会出现明显的“下掉”或“上翘”特征。单井试井分析方法往往将此特征解释为边界的影响，不当的解释结果可能会对生产决策产生误导。为了正确认识多井连通储层的试井特征、甄别疑似边界特征，采用有效井径的概念，建立了无限大均质储层多井系统中测试井井底压力的动态模型，其中测试井考虑表皮效应和井筒储存效应，邻井不考虑表皮效应与井筒储存效应。通过Laplace变换方法，得到了Laplace空间下以Bessel函数表示的精确解，建立了邻井同时生产或同时关井这两种情形下的试井典型曲线图版，进而建立了相应的多井压力恢复试井分析方法。长期渐近解理论分析结果表明：①上述两种情形下，压力恢复导数曲线呈现台阶状上升特征，出现多个径向流水平线，每个水平线高度与第一个水平线高度的比值为测试井与产生影响邻井无量纲产量的代数和；②当邻井一直生产且对测试井产生干扰时，测试井压力恢复导数曲线在中后期呈现下掉特征。

多井系统 压力恢复 典型曲线 双对数分析 压力导数 井间干扰 Laplace变换 渐近解

NATUR. GAS IND. VOLUME 36, ISSUE 5, pp.62-68,5/25/2016. (ISSN 1000-0976; In Chinese)

以单井试井分析[1]和现代产量递减分析技术[2]为核心的气藏动态描述技术[3]在单井井控范围小、井间连通性差的气藏得到了很好的应用。但对于储层渗透性高、井间连通性较好的气藏，其本质是一个多井系统，气藏投产后，测试井的压力恢复资料容易受邻井的影响，压力导数曲线在中晚期会出现明显的“下掉”或“上翘”特征[4-6]；低渗透气藏甜点区试井时也可能出现这种现象。单井试井分析方法往往将此特征解释为边界的影响[7-8]，不当的解释结果可能会对生产决策产生误导。

业内通常采用叠加原理[9-10]方法研究多井系统中测试井的压力动态。林加恩等[11-20]建立了一套比较完善的油藏注采系统压力恢复试井分析方法；Marhaendrajana等[21]建立了考虑邻井生产时的气井多井压力恢复试井分析方法，解释结果有了一定的改善；刘启国等[22-23]建立了两口井共同生产情形的干扰试井典型曲线图版，贾永禄等[24-26]将其扩展到了无限大均质储层有限多井情形。上述研究都发现了压力恢复导数曲线晚期“上翘”现象，但并未对此现象从理论上给予证明。

笔者基于前人的研究成果，建立无限大均质储层中多井试井有效井径模型，绘制测试井在邻井同时生产或同时关井这两种情形下的典型曲线；通过对压力导数特征进行深入的理论研究，最终建立了邻井干扰条件下的多井压力恢复试井分析方法。

其余N-1口邻井的定解问题中扩散方程、初始条件、外边界条件与测试井情形相同，但内边界条件应表示为

1.2模型求解

在Laplace空间下，测试井的井底压力精确解为

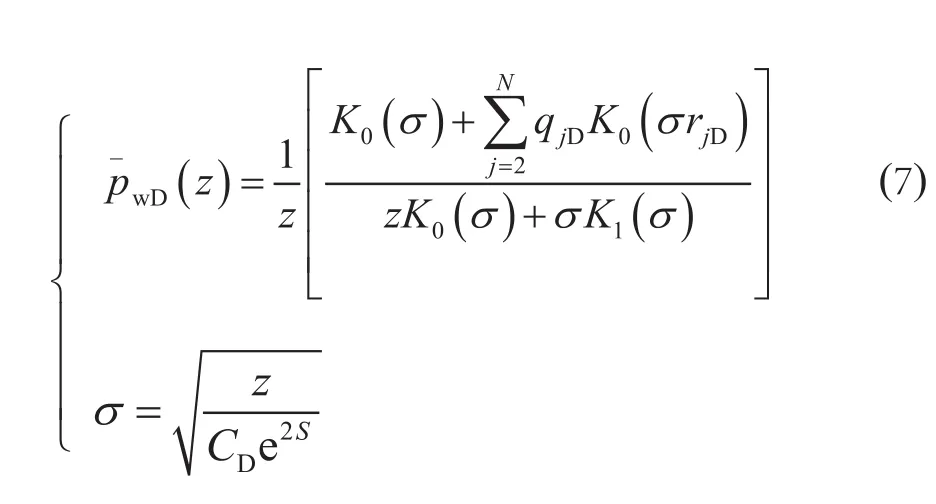
在Laplace空间下，邻井在测试井处的压力响应为

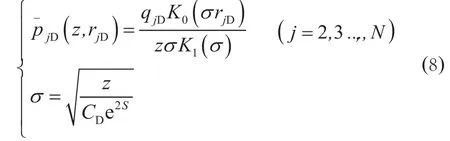
1　无限大均质储层中多井系统试井典型曲线

1.1多井系统试井模型

假设无限大均质储层中有N口井分别以恒定的产量进行生产，忽略重力与毛细管力的影响，测试井考虑表皮效应和井筒储存效应的影响，邻井不考虑表皮效应与井筒储存效应的影响。基于有效井径模型的测试井（下标1为测试井）定解问题[27]可描述为：

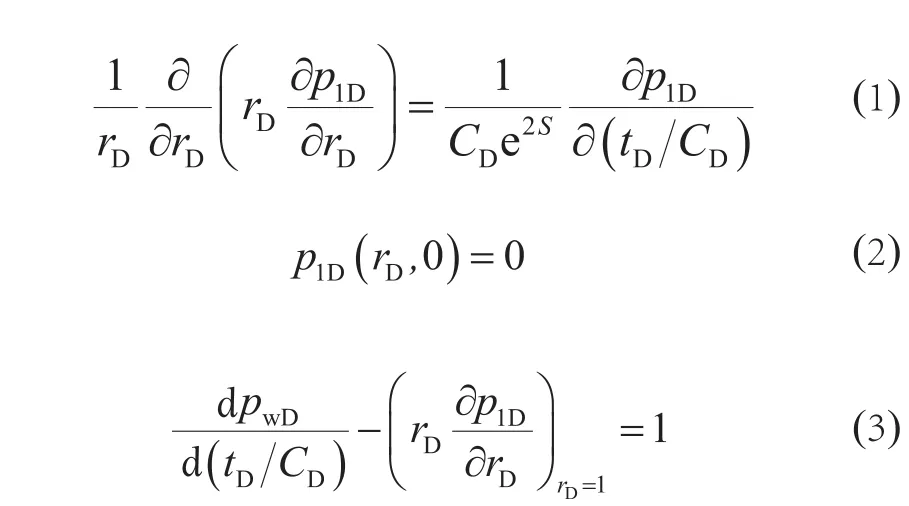
井底压力的实空间解可用Stehfest[28]数值反演方法求得。若邻井产量均为零，式（7）即为无限大均质储层中一口井定产生产时的有效井径模型井底压力解[29]。若为气藏，无量纲压力应采用规整化拟压力形式，无量纲时间采用规整化拟时间[1]形式，解的形式与式（7）、式（8）相同。

1.3多井同时生产情形压降典型曲线特征分析

1.3.1 邻井产量不同、井距不同的情形

由式（7）可知，邻井对测试井井底压力的影响主要取决于邻井的产量和该井与测试井的距离。图1为无限大均质储层中4口井同时生产时的压降曲线，情形（a）中3口邻井的无量纲产量依次为1.0、3.0、5.0，相应的无量纲井距为103、104、105；情形（b）中邻井的无量纲产量仍为1.0、3.0、5.0，但无量纲井距为105、104、103。两种情形的压力导数曲线都出现4个径向流水平线，邻井与测试井距离越近，对曲线产生影响的时间越早。

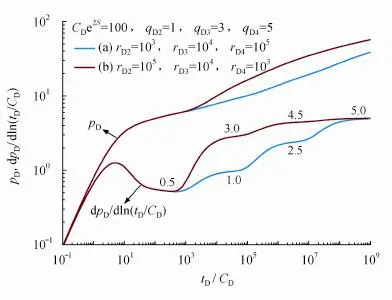
图1　无限大均质储层多井系统各井同时生产时的压降典型曲线

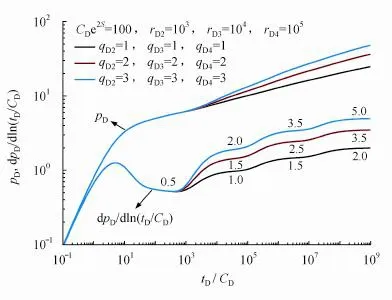
图2　无限大均质储层多井系统各井同时生产时的压降典型曲线

如情形（a）所示：第一径向流段（0.5线）之前部分，为测试井自身特征的反映；第二径向流段（1.0线）为测试井与最近邻井生产特征的反映，这与测试井位于一条封闭断层附近时的特征类似；第三径向流段（2.5线）为测试井与最近2口邻井生产特征的反映；第四径向流段（5.0线）为测试井与3口邻井生产特征的反映。第二、三、四径向流水平线的高度与第一径向流水平线的高度之比为测试井与产生影响的邻井无量纲产量的代数和，即：，X表示对测试井产生影响的邻井数量。如：情形（a）第四径向流水平线的高度与第一径向流水平线的高度之比为5.0/0.5=10.0，这与4口井的无量纲产量代数和相等，即：＝1.0+1.0+3.0+5.0=10.0。情形（b）亦是如此，此时＝1.0+5.0+3.0+1.0=10.0。

1.3.2 邻井产量相同、井距不同的情形

若邻井产量相同，与测试井井距不同，此时亦出现四条径向流水平线，如图2所示。压力导数曲线特征与图1所示特征相同，第一径向流段为测试井自身特征的反映（0.5线）；第二、三、四径向流水平线的高度与第一径向流水平线的高度之比为测试井与产生影响的邻井无量纲产量的代数和。

1.3.3 邻井井距接近的情形

若邻井与测试井井距大致相同，此时只出现两条径向流水平线，如图3所示。第一径向流水平线为测试井自身特征的反映（0.5线）；第二径向流水平线为整个系统生产特征的反映（2.0、4.0、5.0线）。

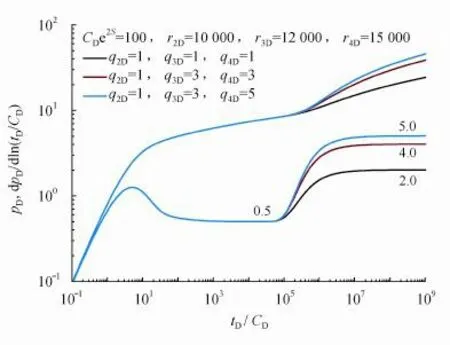
图3　无限大均质储层多井系统各井同时生产时的压降典型曲线

1.3.4 多井同时生产情形下压降典型曲线特征的理论分析

当变量σ足够小时，Bessel函数具有如下性质[30]，有

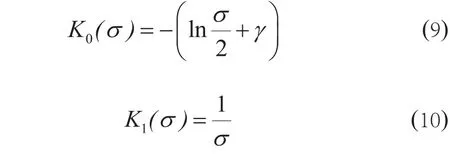
将式（9）、式（10）带入式（7）并求Laplace逆变换，有

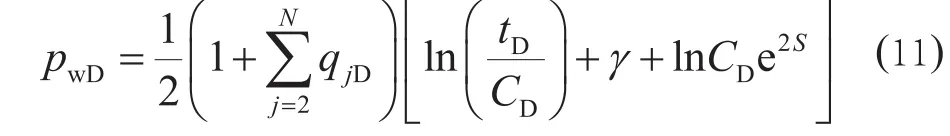
式（11）关于对数时间求导，有

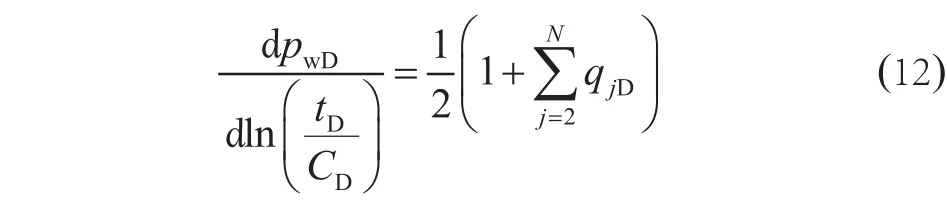
可见，在晚期时间段内，多井同时生产情形的压降导数曲线径向流水平线数值与单井径向流水平线数值之比为测试井与连通井无量纲产量的代数和，即：。因此，当压力导数曲线呈现台阶上升特征时，可能是不渗透边界或外围变差的径向复合模型特征的反映，也可能是由井间干扰造成的。

1.4多井同时关井情形压力恢复典型曲线特征及压力恢复试井分析方法

1.4.1 多井同时关井情形压力恢复典型曲线特征分析

当测试井与邻井同时关井时，多井系统的压力恢复典型曲线如图4所示。当时，压降曲线与压力恢复曲线基本重合。当满足半对数近似条件时，无量纲关井恢复压力关于的导数为：

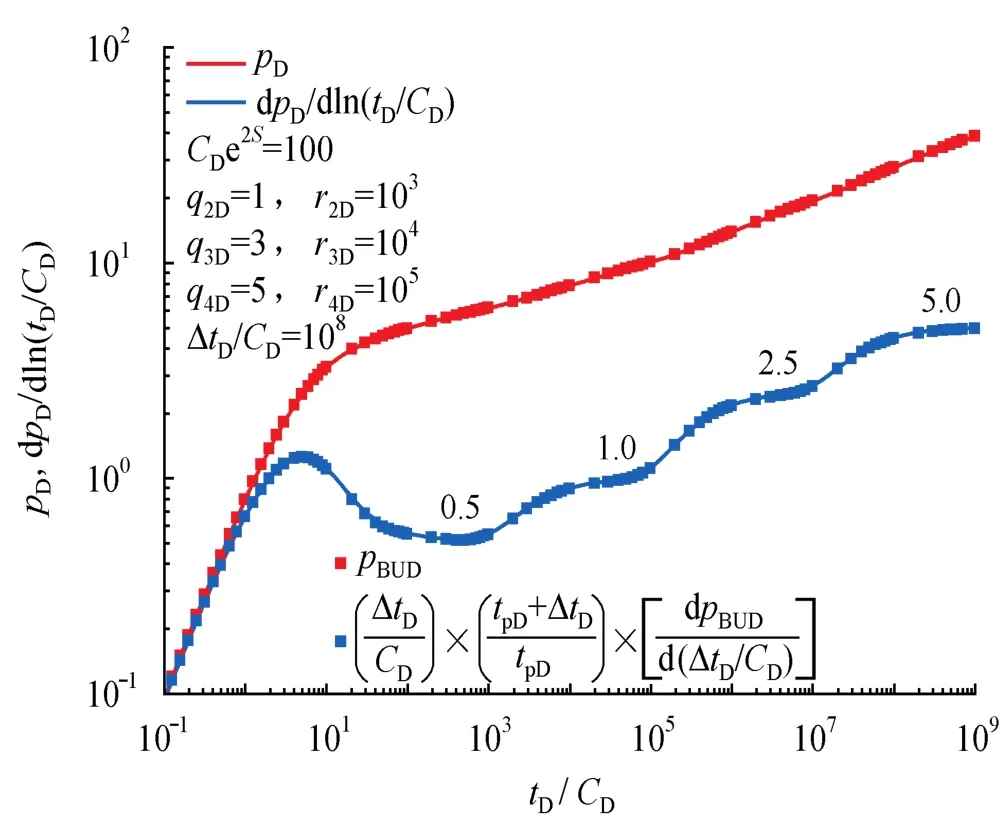
图4　无限大均质储层多井系统中压降与压力恢复典型曲线对比图

因此，当邻井同时关井且对测试井产生干扰时，测试井压力恢复导数曲线在中后期会逐渐“上翘”。

1.4.2 多井同时关井情形压力恢复试井分析步骤

多井系统中压力恢复试井解释拟合步骤与单井系统基本相同[31]，主要步骤如下：

2）利用压降典型曲线图版进行拟合。根据横坐标拟合值、纵坐标拟合值及曲线拟合值，分别计算地层系数Kh、表皮系数S以及井筒储存系数C等参数。

3）计算每个径向流水平线高度与第一径向流水平线高度的比值，即：，进而估算邻井干扰出现的次序及数量。

4）根据双对数分析结果，可进一步开展数值试井历史拟合分析，精细化解析试井分析结果。

2　实例分析

某气藏两口气井同时长期生产，用永久式井下压力计进行动态监测。气藏基础参数如表1所示。测试井以40×104m3/d的平均产量生产10 000 h后进行第1次压力恢复测试，关井时间1 000 h；随后再次以40×104m3/d的平均产量生产了5 000 h后进行第2次压力恢复测试，关井时间2 000 h。邻井以120×104m3/d的产量持续生产了16 000 h后，在测试井第2次压力恢复测试时同时关井。

两次压力恢复测试双对数图如图5所示，导数曲线形态后期完全相反。第1次压力恢复测试，导数曲线后期下降，原因可能为：①储层外围变好；② 邻井生产干扰。采用与1.4.1部分相同的方法，可以证明当邻井一直生产时，测试井压力恢复渐近解的导数为

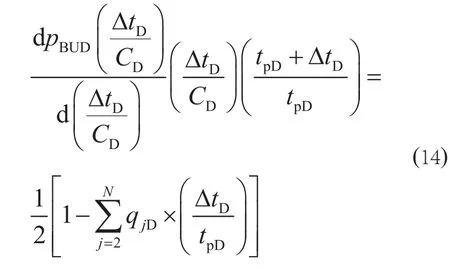
表1　实例基础参数数据表

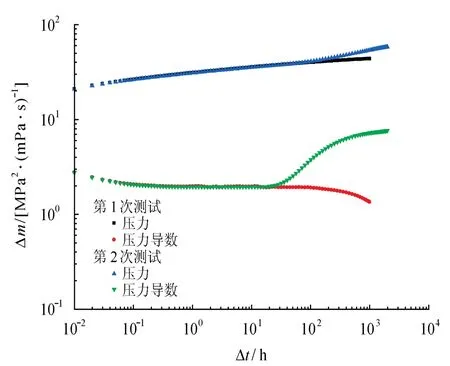
图5　两次压力恢复测试双对数对比图

因此，当邻井一直生产且对测试井产生干扰时，测试井压力恢复导数曲线在中后期会逐渐“下掉”“下掉”速度取决于产生干扰的邻井无量纲产量代数和以及关井时间与关井前生产时间的比值

第2次压力恢复测试导数曲线“上翘”，原因可能如下：①储层外围变差；②边水特征，由于水相黏度比气相黏度高很多，水驱气藏也会表现出类似储层外围变差的特征[32]；③一条或多条不渗透边界；④邻井同时关井干扰。

若采用外围变差的复合模型进行解释，第2次测试双对数拟合结果如图6所示，双对数结果拟合较好，但是历史拟合图拟合不好（如图7所示），加之两次压力恢复测试结果对储层的认识背道而驰，因此不宜选用复合模型进行解释。

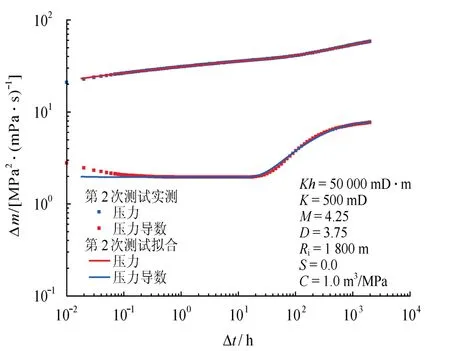
图6　第2次压力恢复测试双对数拟合图

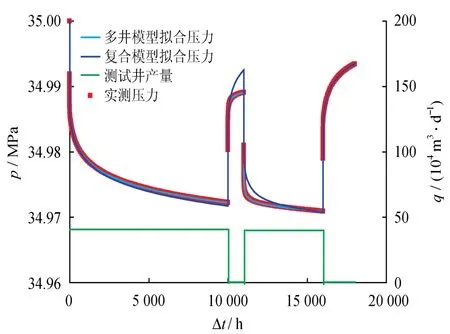
图7　压力历史拟合图

地质研究成果表明，该气藏平面展布很好，没有大的断层或裂缝存在，测试井远离气藏边界；第1次压力恢复测试后期压力导数“下掉”可能是邻井生产造成的，第2次压力恢复测试后期压力导数“上翘”可能是邻井同时关井造成的。因此，排除其他可能性，选用多井模型进行分析，第二次压力恢复测试双对数拟合结果如图8所示。

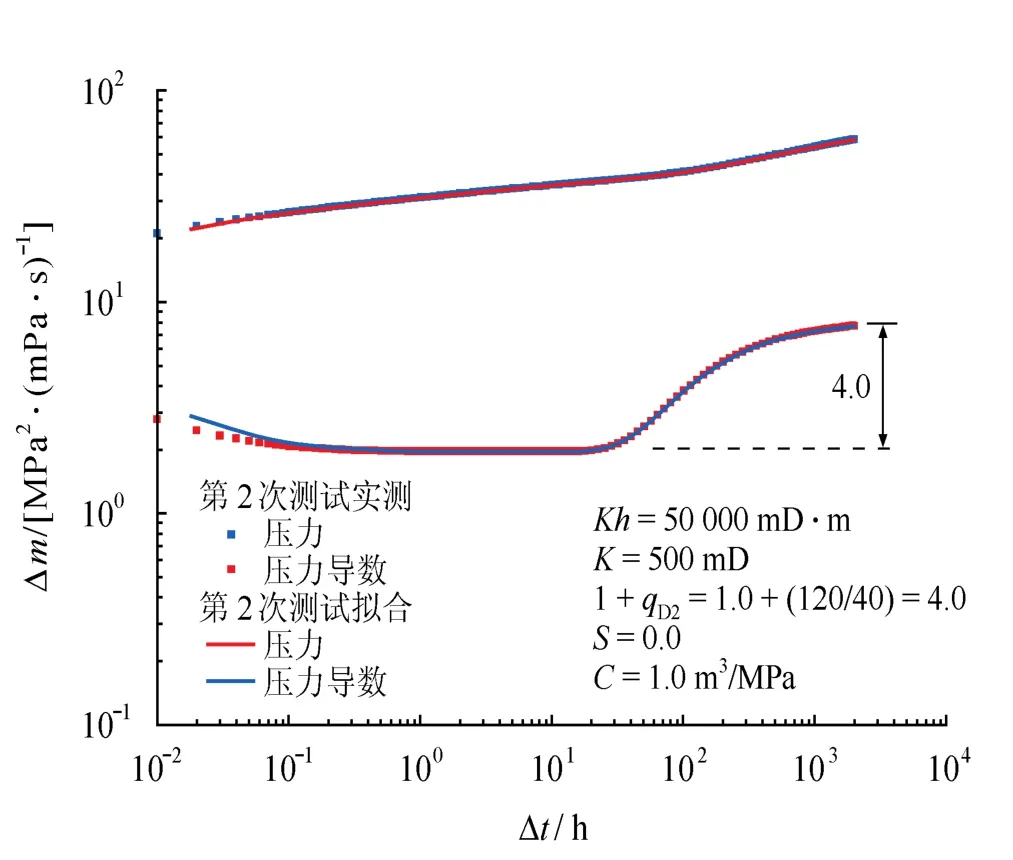
图8　第2次压力恢复测试双对数拟合图

K、S、C解释结果与复合模型情形相同；压力导数曲线两个水平段高程之比为8.0/2.0=4.0，正好是测试井与邻井产量之和与测试井产量的比值，即：(40+120)/40=4.0；导数拟合曲线较图6也有明显改观；历史拟合图拟合良好，如图7所示。

综合分析上述研究成果后认为，多井解释结果是一个比较合理的解释：储层表现出无限大均质特征，渗透率为500 mD，井间连通性好，生产已经发生干扰。此认识将为开发方案中合理井距论证提供有效的技术支持。

3　结论

1）压力恢复导数曲线出现多个上升的台阶，储层模型可能为：①外围变差的复合模型；②一条或多条不渗透边界；③对气井来说，也可能是边水特征的反映；④井间干扰的影响。

2）无限大均质储层中多井同时生产与同时关井情形的压降与压力恢复导数曲线呈现台阶状上升特征，每个水平线高度与第一个水平线高度的比值为测试井与产生影响的邻井无量纲产量的代数和。

3）多井系统中，若邻井一直生产，测试井的压力恢复导数曲线在中后期呈现逐渐“下掉”特征，下掉速度取决于产生影响的邻井无量纲产量的代数和以及关井时间与关井前生产时间的比值。

4）对于一个新探明的气藏，辨别储层边界与邻井的干扰特征可通过两次压力恢复测试实现，第1次压力恢复时邻井保持生产，第2次压力恢复时邻井与测试井同时关井。

5）多井试井分析技术与多井现代产量递减分析技术相结合，可以对连通性较好的气藏做出科学的动态描述，进而为开发技术政策的制定与优化调整提供技术支持。

符号说明

B表示体积系数，无量纲；C表示测试井的井筒储存系数，m3/ Pa；Ct表示综合压缩系数，1/ Pa；h表示储层厚度，m；K表示渗透率，m2；K0、K1分别表示变形第二类零阶与一阶的Bessel函数；m表示气井拟压力，定义为Δm表示拟压力差，单位均为MPa2/mPa·s；pi表示储层原始压力，Pa；表示Δt时刻的关井恢复压力，表示Δt时刻的关井井底压力，表示关井时刻的井底流动压力，单位均为MPa；qj表示第j口井的产量，m3/s；rw表示井筒半径，m；rj表示邻井与测试井的距离，m；S表示测试井的表皮系数，无量纲；z表示Laplace变量，对应的实空间变量表示。无量纲井筒储存系数定义为无量纲压力定义为无量纲距离定义为无量纲产量定义为表示无量纲关井前生产时间；ΔtD表示无量纲关井时间；γ表示无量纲时间定义为欧拉常数，其数值为0.577 2；φ表示孔隙度；μ表示流体黏度，Pa·s。

[1] Spivey JP, Lee WJ. Applied well test interpretation[M]//SPE Textbook Series Vol.13. Richardson: SPE, 2013: 1-30.

[2] Sun Hedong. Advanced production decline analysis and application[M]. Oxford: Gulf Professional Publishing, 2015: 263-290.

[3] Zhuang Huinong. Dynamic well testing in petroleum exploration and development[M]. Amsterdam: Elsevier, 2012: 300-450.

[4] 林加恩, 刘尉宁, 陈钦雷. 多井系统中压力恢复曲线特征[J].大庆石油地质与开发, 1994, 13(4): 56-59. Lin Jia'en, Liu Weining, Chen Qinlei. Production engineering characteristics of pressure buildup curve for a well in a multiwell system[J]. Petroleum Geology & Oilfi eld Development in Daqing, 1994, 13(4): 56-59.

[5] 陈文龙, 吴年宏, 杨勇, 向文刚, 陆爱林. 现代试井分析在牙哈凝析气田的应用[J]. 新疆石油地质, 2004, 25(1): 87-89. Chen Wenlong, Wu Nianhong, Yang Yong, Xiang Wengang, Lu Ailin. Application of modern well test analysis in Yaha condensate gas fi eld, Tarim Basin[J]. Xinjiang Petroleum Geology, 2004, 25(1): 87-89.

[6] 贾永禄, 刘涛, 聂仁仕, 邓祺, 冯晓东, 贾金伟, 等. 涩北气田全气藏关井测试资料特征分析[J]. 科学技术与工程, 2015, 15(27): 23-28. Jia Yonglu, Liu Tao, Nie Renshi, Deng Qi, Feng Xiaodong, Jia Jinwei, et al. The characteristics analysis of Sebei Gas Field all gas wells shut in test data[J]. Science Technology and Engineering, 2015, 15(27): 23-28.

[7] Ramey HJ, Cobb WM. A general pressure buildup theory for a well in a closed drainage area[J]. Journal of Petroleum Technology, 1971, 23(12): 1493-1505.

[8] Kumar A, Ramey HJ. Well test analysis for a well in a constant pressure square[J]. SPE Journal, 1974, 14(2): 107-116.

[9] Onur M, Serra KV, Reynolds AC. Analysis of pressure buildup data from a well in a multiwell system[J]. SPE Formation Evaluation, 1991, 6(1): 101-110.

[10] 李顺初, 周荣辉, 黄炳光. 邻井干扰压力理论分析及其应用[J].石油勘探与开发, 1994, 21(1): 84-88. Li Shunchu, Zhou Ronghui, Huang Bingguang. An analysis of the theory of pressure interference in an adjacent well and its application[J]. Petroleum Exploration and Development, 1994, 21(1): 84-88.

[11] 林加恩, 刘尉宁, 陈钦雷. 多井系统中的压力恢复分析理论 [J].油气井测试, 1993, 2(4): 51-58. Lin Jia'en, Liu Weining, Chen Qinlei. Pressure buildup analysis for a well in a pressure-maintained system[J]. Well Testing, 1993, 2(4): 51-58.

[12] 林加恩, 刘尉宁, 陈钦雷. 注水开发多井系统试井分析理论的应用[J]. 石油勘探与开发, 1996, 23(3): 58-63. Lin Jia'en, Liu Weining, Chen Qinlei. Application of the well test analysis theory to a multiwell water flooding system[J]. Petroleum Exploration and Development, 1996, 23(3): 58-63.

[13] 董剑霞, 翟云芳. 多井干扰条件下的试井理论曲线研究[C]//第五届全国渗流力学学术讨论会论文集(渗流力学进展). 北京：石油工业出版社, 1996: 188-193. Dong Jianxia, Zhai Yunfang. Well test analysis type curves with multiwell interference[C]// Proceedings of the 5thNational Conference of Fluid Flow in Porous Media (Advance on Fluid Flow in Porous Media). Beijing: Petroleum Industry Press, 1996: 188-193.

[14] Dong Jianxia, Zhai Yunfang, Yang Jing, Zhao Chunshen. Determination of injection production ratio size by type curve analysis[C]//SPE Asia Pacifi c Improved Oil Recovery Conference, 25-26 October 1999, Kuala Lumpur, Malaysia. DOI:http://dx.doi. org/10.2118/57320-MS.

[15] Lin Jia'en, Yang Huizhu. Pressure buildup analysis for a well in a closed, bounded multiwell reservoir[J]. Chinese Journal of Chemical Engineering, 2005, 13(4): 441-450.

[16] Lin Jia'en, Yang Huizhu. Analysis of two phase flow pressure buildup data from well in an infi nite multiwell reservoir[J]. Journal of Hydrodynamics (Series B), 2005, 17(4): 489-497.

[17] Lin Jia'en, Yang Huizhu. Analysis of welltest data in a multiwell reservoir with water injection[C]//SPE Annual Technical Conference and Exhibition, 11-14 November 2007, Anaheim, California, USA.DOI: http://dx.doi.org/10.2118/110349-MS.

[18] 李学文, 罗江涛. 邻井影响的试井分析模型应用研究[J]. 油气井测试, 2009, 18(2): 5-7. Li Xuewen, Luo Jiangtao. Application of well test analysis model infl uenced by neighboring wells[J]. Well Testing, 2009, 18(2): 5-7.

[19] 刘曰武, 陈慧新, 张大为, 周蓉, 刘妍. 存在邻井影响条件下的油井数值试井分析[J]. 油气井测试, 2002, 11(5): 4-7. Liu Yuewu, Chen Huixin, Zhang Dawei, Zhou Rong, Liu Yan. Numerical well test analysis for oil wells in condition of adjacent wells infl uences[J]. Well Testing, 2002, 11(5): 4-7.

[20] 张烈辉, 向祖平, 李允, 李晓平, 刘启国. 井间干扰对油水两相流数值试井曲线的影响[J]. 水动力学研究与进展:A辑, 2006, 21(6): 805-810. Zhang Liehui, Xiang Zuping, Li Yun, Li Xiaoping, Liu Qiguo. The interwell interference effect on numerical well test curve of oil-water phase[J]. Journal of Hydrodynamics (Series A), 2006, 21(6): 805-810.

[21] Marhaendrajana T, Kaczorowski NJ, Blasingame TA. Analysis and interpretation of well test performance at Arun Field, Indonesia [C]//SPE Annual Technical Conference and Exhibition, 3–7 October 1999, Houston, Texas, USA. DOI:http://dx.doi. org/10.2118/56487-MS.

[22] 李成勇, 张燃, 刘启国, 张烈辉. 考虑观察井生产情形下的干扰试井研究 [J]. 试采技术, 2005, 26(2): 8-9. Li Chengyong, Zhang Ran, Liu Qiguo, Zhang Liehui. Interference well testing analysis when responding well is producing[J]. Well Testing and Production Technology, 2005, 26(2): 8-9.

[23] 刘启国, 陈彦丽, 张烈辉, 王伟. 不关井干扰试井模型和解释方法研究[J]. 油气井测试, 2006, 15(1): 10-12. Liu Qiguo, Chen Yanli, Zhang Liehui, Wang Wei. Study for disturbing test model with the well opening and its interpreting method[J]. Well Testing, 2006, 15(1): 10-12.

[24] 曾桃, 贾永禄，王海涛，唐东，张武. 有限多井系统试井模型及样板曲线分析[J]. 新疆石油地质, 2006, 27(1): 86-88. Zeng Tao, Jia Yonglu,Wang Haitao,Tang Dong, Zhang Wu. Well testing model for fi nite multiwell system and type curve analysis [J]. Xinjiang Petroleum Geology, 2006, 27(1): 86-88.

[25] 刘永良, 贾永禄, 康毅力, 霍进. 考虑热损失的稠油热采有限多井试井模型[J]. 钻采工艺, 2008, 31(1): 79-81. Liu Yongliang, Jia Yonglu, Kang Yili, Huo Jin. Finite multiwell testing model for heavy oil thermal recovery under consideration heat loss[J]. Drilling & Production Technology, 2008, 31(1): 79-81. [26] Deng Qi, Nie Renshi, Jia Yonglu, Wang Xiaolu, Chen Yangyang, Xiong Yu. A new method of pressure buildup analysis for a well in a multiwell reservoir[C]//SPE North Africa Technical Conference and Exhibition, 14-16 September 2015, Cairo, Egypt. DOI:http://dx.doi.org/10.2118/175866-MS.

[27] Agarwal RG, Al-Hussainy R, Ramey HJ. An investigation of wellbore storage and skin effect in unsteady liquid fl ow: I. Analytical treatment[J]. SPE Journal, 1970, 10(3): 279-290.

[28] Stehfest H. Algorithm 368: Numerical inversion of Laplace transforms [J]. Communications of the ACM, 1970, 13(1):47-49.

[29] 张义堂, 童宪章. 试井分析中有效井径模型、表皮效应模型及其压降解、样板曲线对比[J]. 石油学报, 1991, 12(2):51-60. Zhang Yitang, Tong Xianzhang. A comparision of the effective radius model and the skin effect model as well as their pressure solutions and type curves in well test analysis[J]. Acta Petrolei Sinica, 1991, 12(2): 51-60.

[30] Abramowitz M, Stegun IA. Handbook of mathematical functions [M]. New York: Dover Publications, 1966: 374-375.

[31] Bourdet D, Whittle TM, Douglas AA, Pirard YM. A new set of type curves simplies well test analysis[J]. World Oil, 1983, 196(6): 95-106.

[32] Chen CC, Chu WC, Sadighi S. Pressure-transient testing of gas reservoirs with edge-water drive[J]. SPE Formation Evaluation, 1996, 11(4): 251-256. DOI: http://dx.doi.org/10.2118/28381-PA.

（修改回稿日期 2016-03-08编 辑 居维清）

Pressure buildup analysis in multi-well systems under interferences from adjacent wells

Sun Hedong
(Langfang Branch of PetroChina Research Institute of Petroleum Exploration and Development, Langfang, Hebei 065007, China)

Some gas reservoir has high permeability, and good interwell continuity. This kind of gas reservoir actually can be regarded as multi-well system. After gas reservoir put into production, pressure buildup data is easily affected by offset wells. Middle or late period of pressure derivative curve will be downwarping or upwarping obviously. This kind of characteristic curve would be interpreted as boundary effect based on normal pressure buildup analysis theory. Incorrect analysis will provide incorrect information for misleading development and production decision. In order to clarify reservoir characteristic and identify pressure buildup characteristics by offset effect, the dynamic model of bottom-hole pressure in the multi-well system of infinite homogeneous reservoirs is derived with the parameter of effective radius. Skin and wellbore storage effect are considered for testing well in the model. But skin and wellbore storage are ignored for offshet well. With Laplace transform method, the exact solution to Bessel function in the Laplace space is obtained. Two type curves are plotted for online or offline simultaneous with offset wells. In addition, the type curve characteristics are analyzed and the related method of pressure buildup analysis is established. Under both scenarios mentioned above, analysis on long-term asymptotic theory for solutions shows that the pressure derivative curves rise step-likely, and there appears a multi-radial flow stabilization line. The ratio of each stabilization line height to the first stabilization line height is the algebraic sum of the dimensionless production combined testing well and effective offset well. In the meanwhile, the pressure derivatives curves descend under the scenario of test well buildup when offset wells are producing simultaneously.

Multi-well system; Pressure buildup; Typical curve; Log-log analysis; Pressure derivative; Interference; Laplace transform; Asymptotic formula

10.3787/j.issn.1000-0976.2016.05.009

国家科技重大专项“大型油气田及煤层气开发——致密砂岩气有效开发评价技术”（编号：2011ZX05013-002）。

孙贺东， 1973年生，博士；主要从事气田开发方面的研究工作。地址：（065007）河北省廊坊市万庄44号信箱天然气开发研究所。电话：（010）69213743。ORCID:0000-0002-7673-5041。E-mail:sunhed@petrochina.com.cn