基于优先度的改进最低水平线排样算法

黄 河，许 超

（东南大学 机械工程学院，江苏 南京211100）

0 引言

矩形件排样的优化问题，是将一定数量的矩形件尽可能多地、无重叠地排放到—个定宽、定长（或无限长）的矩形板材上，使其利用率达到最大。矩形件排样问题，广泛存在于钣金下料、玻璃切割、电路布局、报刊排版等工业生产中。随着社会生产力的不断提高，生产规模不断扩大，原材料的消耗量也越来越大，提高原材料利用率在实际生产中显得越来越重要[1-2]。为此，国内外众多学者在排样领域提出了许多有效的算法。其中启发式算法主要有BL 算法、最低水平线算法、Best-Fit 算法等；由于单一的启发式定位规则难以实现全局优化，许多学者将启发式算法与智能算法（遗传算法、蚂蚁算法等）相结合寻求全局最优解并取得了一些成果，如文献[2]中将最低水平线搜索加上遗传算法等。然而，当排样规模较大时这些算法十分耗时，影响实际生产效率。因此，寻求一种简单快速并在一定程度上可优化排样结果的启发式算法具有重要应用价值。研究表明，最低水平线算法是一种颇具潜力的启发式算法，至今已有许多派生算法，如最低轮廓线搜索算法、旋转最低水平线算法等。本文在分析上述算法的不足的基础上提出基于优先度的改进最低水平线算法，可以有效改善最低水平线算法的排样结果。

1 当前最低水平线算法及其分析

1.1 最低水平线算法基本思想

原始最低水平线算法的基本排样步骤如下[2]：

（1）设初始最高轮廓线为板材最下面的边。

（2）每当排入一个零件就在最高轮廓线集中选取最低的一段水平线。如有数段，则选取最左边的一段，测试该段线的宽度是否大于或者等于要排零件的宽度：①如果该段线的宽度大于要排零件的宽度，则将该零件在此位置排放，同时更新零件的最高轮廓线；②否则，查询最低水平线段相邻的左、右两段水平线，将最低水平线提升至与之相邻且高度较低的一段平齐，更新零件最高轮廓线。

（3）重复第（2）步，直至能排入该零件。

（4）重复上述过程，直至所有零件排放完毕。

从排样过程不难看出，原始的最低水平线算法没有定义零件的排入顺序。由于对零件的搜索极具盲目性，即使给定了零件顺序（如宽度递减排入），其排样结果依然欠佳。

图1 是按宽度递减顺序应用最低水平线算法的模拟排样过程，容易看出由于2 号零件宽度大于最低水平线宽度，使得最低水平线更新至1 号零件上轮廓。而实际更优的排样方案应该是将3 号零件排入当前最低水平线以避免板材右侧区域浪费。

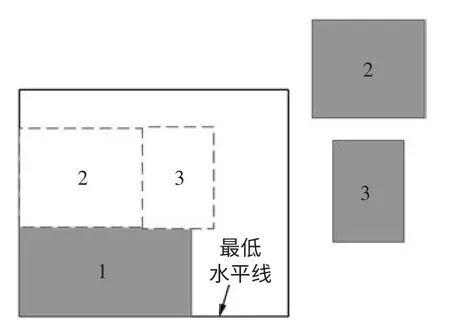
图1 最低水平线算法的排样实例

1.2 已有的改进算法及其分析

许多学者针对最低水平线算法的不足做出了不同程度地改进，这里选取比较有代表性的一种改进算法进行分析。

文献[3]中提到了最低水平线旋转搜索法。该算法对原始算法做出了两点关键改动：引入了搜索和旋转。其具体做法是：若当前零件宽度大于最低水平线宽度，并不立即提升最低水平线，而是将零件旋转90°后再次判断其宽度是否小于最低水平线，若此时零件宽度仍大于最低水平线宽度则向后搜索其他零件；重复上述步骤，直至有合适的零件排入；只有当按上述步骤遍历所有零件仍无法排入时才提升最低水平线。从图2 可以看出该算法的排样效果较原始算法有一定的提升。

图2 改进前后排样结果对比

最低水平线旋转搜索算法虽然扩大了每次排样的零件搜索范围，一定程度上避免了因盲目提升最低水平线造成的板材区域浪费。但是这种搜索方法过于单一，仅仅只是为了找到待排零件队列中首个能够排入当前最低水平线的零件，而不是寻找一个排入后能对全局优化目标贡献最大的零件。换句话说，该搜索算法难以找到“最适合”排入当前最低水平线的零件。通过图3 的例子可以清楚地说明这一问题。

上述例子中，在第二次排入时，最低水平线旋转搜索算法首先发现2 号零件旋转后可以排入最低水平线，因此忽略了更适合排入当前最低水平线的3 号零件，导致排样图出现图示的“高塔”，不仅浪费了右侧板材区域，而且不利于板材的后续利用。

图3 最低水平线旋转搜索算法缺陷示例

经过以上分析，为了使排样结果更趋近全局最优解，必须寻找一种更加有效的搜索规则，使得基于该规则的每一次排入都能达到局部最优，并且尽可能地使后续排样过程朝着最优方向发展。

2 基于优先度的最低水平线改进算法设计

2.1 优先度函数的设计

基于优先度的搜索规则实际上与现实生活中高考录取规则十分相似。高校以考生的各科总成绩这个综合量化指标来择优录取；同样的，每一次的排样过程也是一个“择优”过程，当前最低水平线（好比高校），通过优先度（好比总成绩）这一量化指标来寻找零件队列中最适合排入的对象。总成绩包含一些所占比重不同的科目，同理，优先度也由一些权重不同的影响因子构成。

（1）主影响因子f1

考虑到排样的核心目标是提高板材利用率，减少材料浪费，结合最低水平线算法的特点，将零件的排入宽度（零件排入时的水平尺寸）与当前最低水平线的匹配程度作为主要影响因子f1，其表达式如下：

式中：Wline——最低水平线宽度；

Wpart）——零件排入宽度。

f1的值越小说明当前最低水平线的利用率越高，本次排样造成板材浪费的可能性越小。搜索过程会自动筛选排入宽度小于最低水平线宽度的零件，因此f1的取值范围是[0，1]。

（2）次影响因子f2

每次排样时，除了追求局部利用率的最大化，还应顾全后续的排样过程以及余料的利用，尽可能地使现有的排样图边界整齐，避免出现高度差过大的“台阶”。本文采取控制零件宽长比的方法确保形状接近方形的零件优先排入，为此设计f2的表达式如下：

式中：ratio——零件宽长比，即零件的较大尺寸/零件较小尺寸。

f2的取值越小说明零件宽长比越小，形状越接近方形。由于ratio 不小于1，故f2的取值范围是[0.5，1]。

（3）次影响因子的权重系数

若直接取f1与f2的和作为优先度函数，则当f1取值接近于0 时，f2的值将显著影响优先度函数的取值，这会造成一些不好的排样结果。如图4 中的例子，当前最低水平线宽度为20，现有待排零件3、4，它们的尺寸分别为20×100 和15×15，若取f1+f2的值作为优先度函数值，则经过计算后发现4 号零件的计算值要小于3 号，即4 号零件优先于3 号零件排入，这显然是不合理的。

图4 特定情况下的缺陷示例

为此，需要为次影响因子添加一个系数，使得当主影响因子f1取值较小时，次影响因子f2的影响力得到控制。经过反复试验推导，采用如下表达式作为次影响因子权重系数，记为ε。

不难看出ε 的取值范围是[0.2，1.1]，且单调递增，当f1取值接近0 时，次影响因子受到了有效的约束。总结上述分析可最终确定优先度函数F 的表达式如下：

利用公式（4）重新计算图4 中两个待排零件的优先度值，发现此时3 号零件的计算值小于4 号零件，使排样结果得到了优化。

需要说明的一点是，此处优先度函数F 的取值越小代表零件在队列中优先度越高，并不是F 取值越大优先度越高。

2.2 算法的基本思路

排样之前，首先将所有待排零件调整至横放状态（即水平尺寸大于等于竖直尺寸），并按照水平尺寸（宽度）递减的顺序组成待排零件队列。对于宽度为L 的当前最低水平线，首先剔除零件队列中宽度与高度均大于L 的零件，若剩余零件个数为0，则更新最低水平线至与其相邻的较低水平线，重复上述操作；若剩余零件个数不为0，则在剩下的零件中，令Wi为第i（i=0，1，2…n）个零件的排入宽度，mark为已计算零件中最优零件标记，Fmin为已计算零件中F 最小值，rotate 为旋转标志，单次排样流程如图5所示。一个完整的排样过程就是重复执行单次排样操作，直至所有零件均已排入，或板材已耗尽，最终输出排样图。

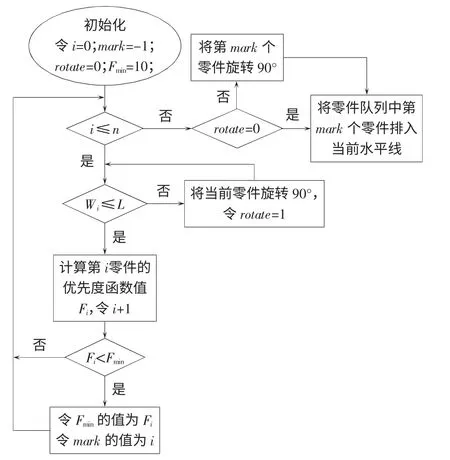
图5 单次排样流程图

3 实例计算

作者在VisualStudio2003 开发环境中用C++语言编写了基于优先度的改进最低水平线算法以及最低水平线旋转搜索算法的程序，将文献[5]中的部分实验用例在PC 机进行了仿真，并对比了实验结果。每组实验采用的是宽度一定高度不限的板材，用排样高度来表征板材利用率。表1 列出了实验所用数据，表2、表3 是实验结果对比。

表1 所用的实验数据

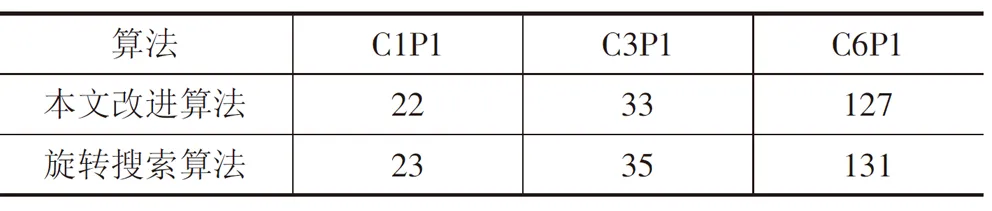
表2 两最低水平线改进算法的排样高度比较

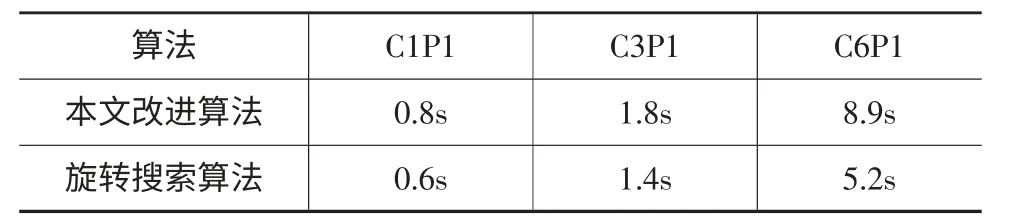
表3 两种最低水平线改进算法的排样时间比较

对比表2 中的数据发现，对于所选实验用例，本文改进算法的排样利用率要优于最低水平线旋转搜索算法，排样时间虽然略有加长，但在可接受范围内。部分排样结果如图6 所示。

4 结论

本文在分析原始最低水平线算法及其派生算法不足的基础上引入优先度的概念，利用优先度函数来提高零件搜索的精确性，一定程度上克服了现有最低水平线算法搜索过程的盲目性，优化了排样结果。实验结果表明，本文的改进算法在利用率方面相比现有最低水平线算法有了一定提高；与当前主流的启发式加智能算法的综合排样算法相比，利用率虽并无优势，但计算时间大大减少。

综合来看，本文算法能不依赖智能算法而取得较接近最优解的排样结果，具有较强的实用性。

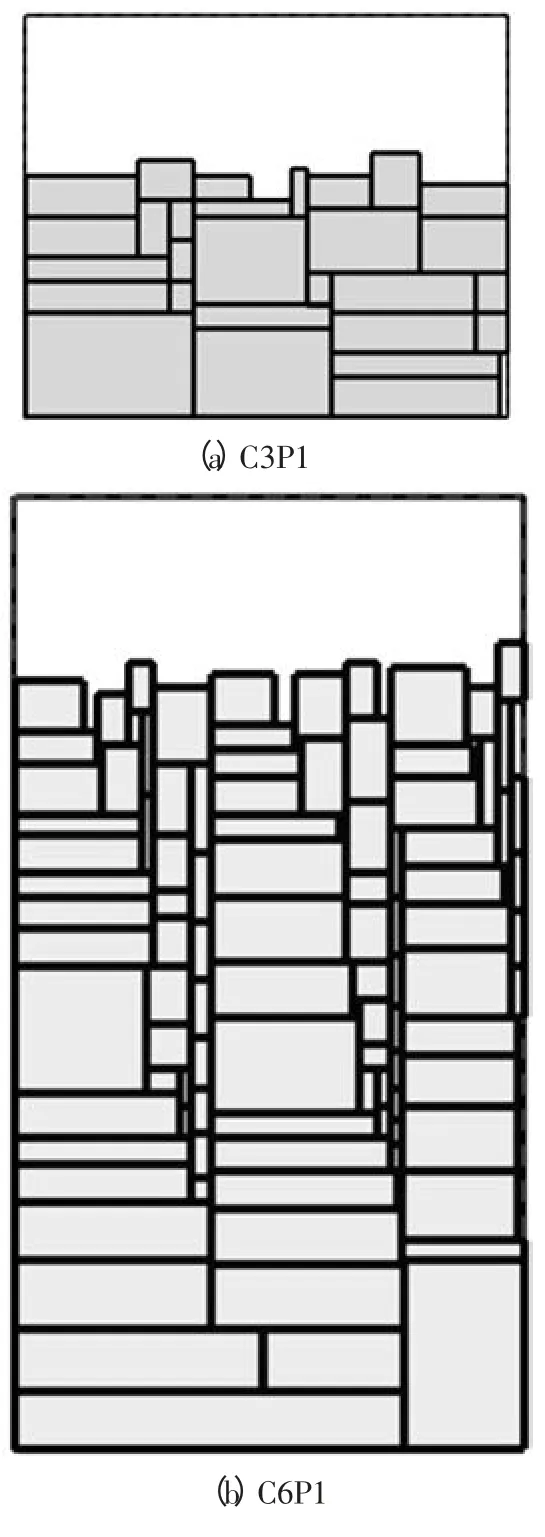
图6 排样结果实例

[1]陈仕军，曹 炬.矩形件优化排样的一种启发式算法[J].计算机工程与应用，2010，46（12）：230-232.

[2]赵晓东.矩形件优化排样算法的研究与实现[D].大连：大连交通大学，2008.

[3]李 捷.一种矩形件布局问题的求解方法[J].科技广场，2008，（1）：22-24.

[4]杨传华，吴锦文，等.定序列矩形件优化排样的二维搜索算法[J].佳木斯 大 学 学 报，2010，28（3）：354?356.

[5]Hopper E，Turton B.An empirical investigation of meta—heuristic and heuristic algorithms for a 2D packing problem [J].European Journal of Operational Research，2001，128(1)：34-57.

[6]Ender O¨zcan, Zhang Kai,John H.Drake Bidirectional best -fit heuristic considering compound placement for two dimensional orthogonal rectangular strip packing [J].Expert Systems with Applica tions ,2013 (40):4035-4043.

[7]王竹婷，刘 林，等.改进的最低水平线搜索算法求解矩形排样问题[J].工程设计学报，2009，16（2）：98?102.

[8]贾志欣，李红林，等.异形件排样的综合优化算法[J].锻压装备与制造技术，2004，39（1）：59-61.

[9]李 勇，曹 矩，等.矩形件排样优化的十字线法[J].锻压装备与制造技术，2004，39（6）：98-99.