含天然气水合物沉积物三维孔隙结构数值重建
曾建邦 胡高伟 李隆键 陈 强 吴能友 王广君
1. 载运工具与装备教育部重点实验室·华东交通大学 2. 青岛海洋国家实验室海洋矿产资源评价与探测技术功能实验室3. 国土资源部天然气水合物重点实验室·青岛海洋地质研究所 4. 低品位能源利用技术及系统教育部重点实验室·重庆大学
含天然气水合物沉积物三维孔隙结构数值重建
曾建邦1,2,3,4胡高伟2,3李隆键4陈强2,3吴能友2,3王广君1
1. 载运工具与装备教育部重点实验室·华东交通大学 2. 青岛海洋国家实验室海洋矿产资源评价与探测技术功能实验室3. 国土资源部天然气水合物重点实验室·青岛海洋地质研究所 4. 低品位能源利用技术及系统教育部重点实验室·重庆大学
曾建邦等.含天然气水合物沉积物三维孔隙结构数值重建. 天然气工业,2016,36(5):128-133.
三维孔隙结构重建是揭示沉积物内天然气水合物(以下简称水合物)形成机理及分布规律的基础和前提。在现有的数值重建方法中,模拟退火法被广泛应用。为使该方法的重建结构更加接近于实际,对该方法进行了改进,所构建的数值重建模型能够纳入沉积物颗粒形状(包括圆球状、椭球状、扁球状、长扁球状、片状和针状)、尺寸分布(如正态分布)以及水合物分布模式(如胶结状、悬浮状或颗粒状)等重要结构与统计信息,并利用改进后的模型对含水合物沉积物的三维孔隙结构进行了数值重建。最后,对重建的沉积物(不含水合物)孔隙结构进行特征化分析,可获得沉积物内孔隙率和孔径分布等信息;对重建的含水合物沉积物孔隙结构进行特征化分析,可获得各组分体积分布及其截面平均体积分数沿x轴方向的分布曲线等信息。结论认为:所开发的数值重建模型能够重建出与实际情况较为接近的含水合物沉积物三维孔隙结构,且能揭示水合物分布模式对沉积物孔隙内水(或冰)和天然气空间分布的影响。
含天然气水合物 沉积物 孔隙结构 分布模式 模拟退火法 数值重建 特征化分析
沉积物孔隙结构重建是天然气水合物介观孔(或颗粒)尺度模型的基础和前提,其重建方法有实验和数值两种:实验方法是借助X射线衍射、核磁共振或X-CT等高分辨率仪器对沉积物进行二维或三维成像[1-3],该方法受实验设备价格、样本制备要求、实验操作人员技能与仪器分辨率等条件的限制。因此,借助计算机对沉积物孔隙结构进行重建是一种行之有效的方法。在现有的数值重建方法中,模拟退火法除了可以考虑孔隙率、组元体积分数以及两点相关函数等基本信息之外,还可兼顾更多与沉积物孔隙结构相关的重要信息,因而其重建结构与实际更为接近[4]。目前,该方法已在砂岩[5]、锂离子电池正[6]、负极[7]等复杂孔隙介质的三维重建中得到广泛地应用。
海底沉积物主要有三大来源[8]:①风化物从内陆岩体被剥蚀后经河水携带至出海口,搬运到海中,慢慢沉淀下来的接近球状的沉积物;②火山灰从火山口喷出后经风携带至海上,最后沉积到海底的碎屑岩大致有圆球、椭球、扁球和长扁球状等4种形状;③海洋生物死后沉积到海底,被逐渐溶解、分解后剩下的片状和针状沉积物。水合物在沉积物内的分布模式大多是根据声学和热学探测等手段推测而得[3],大致有以胶结物的形式存在于沉积物颗粒之间(胶结状)[2]、游离于沉积物孔隙中(悬浮状)[9]和与沉积物颗粒一样成为骨架组成部分(颗粒状)[1,10]等3种微观分布状态。为此,笔者将对模拟退火法实施改进,使其可以考虑沉积物颗粒形状和尺寸分布以及水合物分布模式等重要信息,并用于重建含水合物沉积物的三维孔隙空间,再对重建孔隙结构进行特征化分析,探讨水合物分布模式对沉积物孔隙内水(或冰)和天然气空间分布的影响。
1 含水合物沉积物孔隙结构数值描述
以Jin等[2]制备的甲烷水合物沉积物为例(图1),由于受仪器分辨率的限制,图中仅能分辨出沉积物颗粒、甲烷及水合物和水(或冰)的混合物(文中视为水合物)。在重建过程中,可用相函数I进行描述:

其中r(x, y, z)表示三维空间中任意位置矢量,相i = 0、1、2、3分别代表甲烷、沉积物、水合物和水(或冰)。通过统计平均可得到该结构的基本统计信息,如相i的体积分数εi= <Ii(r)>;两点相关函数fij(r1, r2) = <Ii(r)Ij(r)>,表示在重构区域内距离为u的两位置点r1、r2分别属于i相和j相的概率,代表孔隙结构中各相间的空间分布关系。若假定该孔隙结构各向同性,则相关函数简化为:其中

基于图像技术对图1-a红色方框内的图片进行数字化处理得到图1-b,通过统计平均可得到两点相关函数(图2)以及甲烷、沉积物颗粒、水合物和水(或冰)体积分数,分别为0.058 7、0.622 3、0.319 0和0。以10.8 μm作为基本节点尺寸,重建空间区域为Nx= Ny= Nz= 200(即重建区域物理尺寸为Lx= Ly= Lz= 2.16 mm)。重建时,假定重构区域各相同性;沉积物颗粒形状包括圆球、椭球、扁球、长扁球、片和针状[8]。这些颗粒形状均可通过调节椭球3个轴长而得:①当3个轴长相等时为圆球状;②当3个轴长相近时为椭球状;③当2个轴长较大,而另一轴长较小/特小时为扁球/片状;④当1个轴长较长,而另外2个轴长较小/特小时为长扁球/针状。要对空间椭球进行描述,除了上述3个轴长(各轴长的取值范围为[10.8 μm,691.2 μm]与图1中的沉积物颗粒尺寸保持一致,并假定均满足正态分布)外,还需要考虑3个轴的转向角取值范围均为[0°,360°]以及椭球中心坐标,故重建时共需考虑9个参数的变化。

图1 沉积物内胶结状水合物分布图

图2 含甲烷水合物沉积物内各相两点相关函数图
2 模拟退火重建算法及步骤
重建含水合物沉积物三维孔隙空间涉及沉积物骨架、水合物和水(或冰)的重建,具体步骤如下:
1)沉积物颗粒系统初始化。将预设尺寸和形状的颗粒随机放置在重建区域内,接收概率为:

式中v表示当前放置颗粒与已有颗粒重叠部分体积的占比;εv表示调节重叠程度的常数。
该步骤直到重建区域内沉积物颗粒体积分数达到预设值时结束。
2)沉积物颗粒的移动。随机选择一个颗粒,按随机产生的距离dr (dx, dy, dz) 移动该颗粒,dx、dy和dz均满足相同的指数分布,以dx为例:

式中a表示一个控制移动距离的常数。
3)判断是否接收步骤2)的概率为:

式中T表示系统“退火温度”;ΔE = Et+1-Et,Et和Et+1分别表示移动前后系统的能量值。
Et可表示为:

式中N = Nx× Ny× Nz;U表示两位置点r1、r2距离u的最大值;分别表示t时刻含水合物沉积物三维孔隙结构和从图1-b中提取的作为参照的两点相关函数(图2)。
4)重复步骤2)、3),当T = λt+1T0(λ取0.01,为冷却率;T0取1.0,为初始“退火温度”)达到目标温度Tend,则终止计算,得到沉积物颗粒骨架。
5)重建水合物和水(或冰)在沉积物孔隙空间的微观分布,包括如下3种情况:①对于胶结状水合物(水合物和水/冰的混合物),只需采用文献[11]中的模拟退火法对水合物在沉积物内的分布进行重建,但需增加的约束条件有:当水合物移至沉积物颗粒表面时,若不满足式(5),也接受该次运动;判断计算是否终止时,在沉积物颗粒表面不允许出现甲烷,除非除沉积物颗粒表面外,孔隙内已没有水合物。②对于悬浮状水合物,重建时先后采用文献[11]中的模拟退火法对水(或冰)和水合物在沉积物内的分布进行重建,但需增加的约束条件有:沉积物颗粒和甲烷的体积分数与图1-b一致,水合物和水(或冰)的体积分数分别取0.214 5和0.104 5[9];当水(或冰)移至沉积物颗粒表面时,若不满足式(5),也接受该次移动;判断计算是否终止时,在沉积物颗粒表面不允许出现甲烷和水合物,除非除沉积物颗粒表面外,孔隙内已没有水(或冰)。③对于颗粒状水合物。先采用步骤1~4对水合物颗粒进行数值重建,初始预设水合物颗粒形状为球,球半径的取值范围为[10.8 μm,162.0 μm],与文献[10]保持一致,并假定其满足正态分布,水合物体积分数仍然取0.214 5;然后采用文献[11]中构建的模拟退火法对水(或冰)在孔隙内的分布进行数值重建,其体积分数预设值为0.104 5。
3 重建结果分析
3.1重建结果

图3 数值重建的含胶结状水合物沉积物图
基于上节算法分别对含胶结、悬浮和颗粒状水合物沉积物进行重建。重建过程中先对沉积物颗粒执行退火过程,获得其在重建区域的分布图,见图3-a(结构Ⅰ),图4-a(结构Ⅱ)和图5-a(结构Ⅲ)。可见,沉积物骨架均由具有不同大小且形状各异(圆球、椭球、扁球、长扁球、片和针状)的沉积物颗粒组成,但三者间的差别较大,说明模型重建结果具有随机性。然后,对水合物和水(或冰)执行退火过程(其先后顺序见前述文字),获得它们在重建区域的分布(图3-b、图4-b和图5-b),发现相比于含颗粒状水合物沉积物,在含胶结状和悬浮状水合物沉积物内天然气更为集中;在含悬浮状水合物沉积物内水(或冰)分布在沉积物颗粒表面,而在含颗粒状水合物沉积物内其分布规律并不明显。最后,得到含水合物沉积物孔隙结构,(图3-c、图4-c和图5-c),可清楚地观察出水合物在沉积物孔隙空间内的分布规律。
为进一步观察出沉积物颗粒、水合物、天然气和水(或冰)在含胶结状、悬浮状和颗粒状水合物沉积物内的分布形态,可分别对其进行二维切片(图3-d、图4-d和图5-d),均可发现沉积物颗粒、水合物、天然气和水(或冰)之间的分界面十分清晰,且分别与实验拍摄的含胶结状[2]、悬浮状[9]和颗粒状[10]水合物沉积物孔隙结构较为相似。可见,基于笔者所开发的数值重建模型能够重建出与实际较为接近的含水合物沉积物三维孔隙结构。

图4 数值重建的含悬浮状水合物沉积物图

图5 数值重建的含颗粒状水合物沉积物图
3.2特征化分析
分别对如图3-a、图4-a和图5-a所示的沉积物孔隙结构进行特征化分析:可得到其孔隙率(表1)。

表1 水合物赋存状态对重建结果的影响表
从表1中可看出,它们与初始设定值均相差不大(最大相对误差不超过0.32%)。对于沉积物孔径分析,笔者以欧氏距离转换法[12]分别计算结构Ⅰ、Ⅱ和Ⅲ内最大内切球直径[13],统计分析可得到具有不同尺寸孔的相对体积(具有相同半径孔的体积之和与总的孔体积的比值)随孔尺寸大小的分布关系(图6)。从图6中可看出:三者的孔径分布基本一致。另外,笔者还分别计算了它们的平均孔径(表1)。结合图6和表1,可以看出不管是最大孔径还是平均孔径,三者之间的差别均不大。上述情况与实际相符,即海底沉积物的物理变化过程和现象具有随机性,但当统计区域达到一定程度时,其内部相关统计信息(如孔隙率、孔径分布等)却具有一定的规律性[14],进一步说明基于本文构建的重建算法能够较为真实地再现沉积物三维孔隙空间及其内水合物的微观分布规律。

图6 沉积物孔隙空间内孔径分布图
分别对图3-c,图4-c和图5-c所示的含水合物沉积物微结构进行特征化分析,可得到各组分的体积分数(表1),均与初始预设值相差不大(最大相对误差不超过1.0%);还可得到各组分截面平均体积分数沿x轴方向的分布曲线(图7),发现沉积物、水合物、水(或冰)和天然气在各自初始额定份额(或平均体积分数)上下波动,其中波动幅度最大的是沉积物颗粒,并按水合物、水(或冰)和天然气的顺序依次减小。然而,波动幅度并不能描述各组分沿x轴方向分布的均匀程度,须引入各组分在截面n上的平均体积分数)与各自在含水合物沉积物内的平均体积分数()之间的最大相对误差的绝对值(δ1)和平均相对误差的绝对值(δ2),即
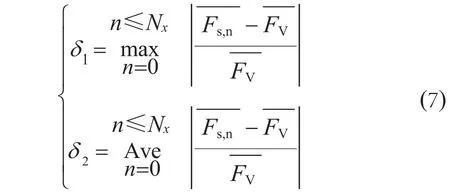
式中Nx表示重建区域在x轴方向上的节点个数。
基于公式(7),分别对含胶结、悬浮和颗粒状水合物沉积物中各组分的δ1和δ2进行计算,(表2)。可见,δ1和δ2最小的均为沉积物,且三者之间差别不大;水合物分布规律不同,对其自身、水(或冰)和天然气的δ1和δ2的影响也不相同,主要体现在:

图7 各组分体积分数沿x轴方向的分布图

表2 水合物赋存状态对δ1和δ2的影响表
①对于含胶结(悬浮或颗粒)状水合物沉积物,δ1和δ2均按水合物、水(或冰)(胶结状不予考虑)和天然气的顺序依次增大,即其内部天然气截面平均体积分数沿x轴方向的变化最为剧烈,并按天然气、水(或冰)和水合物的顺序依次减小;②相比含胶结状水合物沉积物,在含悬浮状水合物沉积物中δ1和δ2更大,即其内部各组分截面平均体积分数沿x轴方向的变化更为剧烈;③相比含胶结和悬浮状水合物沉积物,含颗粒状水合物沉积物中的水合物截面平均体积分数沿x轴方向的变化最为剧烈,但水(或冰)和天然气的变化则相对平缓。可见δ1和δ2能较好地衡量水合物分布模式对含水合物沉积物内各组分分布规律的影响。
4 结论
1)基于模拟退火法构建含水合物沉积物孔隙结构数值重建模型,并以实际孔隙率、组元体积分数、沉积物颗粒形状(圆球、椭球、扁球、长扁球、片状和针状)、尺寸(正态分布)分布、水合物分布模式(胶结、悬浮和颗粒状)和从二维X-CT图像中提取的两点相关函数等重要信息作为模型输入参数,能够重建出与实际较为相似的含水合物沉积物。
2)根据对重建的沉积物和含水合物沉积物孔隙结构特征化分析,可获得沉积物内孔隙率、孔径分布等信息和含水合物沉积物内各组分体积分数及其截面平均体积分数沿x轴方向的分布曲线等信息,可在一定程度上揭示水合物分布模式对沉积物孔隙内水(或冰)和天然气空间分布的影响规律。
3)由于重建孔隙结构的随机性及其相关统计信息的规律性,使得所开发的模型能够重建出与实际更为接近的含水合物沉积物孔隙空间。
[1] Chaouachi M, Falenty A, Sell K, Enzmann F, Kersten M, Haberthur D, et al. Microstructural evolution of gas hydrates in sedimentary matrices observed with synchrotron X-ray computed tomographic microscopy[J]. Geochemistry, Geophysics, Geosystems, 2015, 16(6): 1711-1722.
[2] Jin S, Takeya S, Hayashi J, Nagao J, Kamata Y, Ebinuma T. Structure analyses of artifi cial methane hydrate sediments by microfocus X-ray computed tomography[J]. Japanese Journal of Applied Physics, 2004, 43(8A): 5673-5675.
[3] 胡高伟, 李承峰, 业渝光, 刘昌岭, 张剑, 刁少波. 沉积物孔隙空间天然气水合物微观分布观测[J]. 地球物理学报, 2014, 57(5): 1675-1682. Hu Gaowei, Li Chengfeng, Ye Yuguang, Liu Changling, Zhang Jian, Diao Shaobo. Observation of gas hydrate distribution in sediment pore space[J]. Chinese Journal of Geophysics, 2014, 57(5): 1675-1682.
[4] Hidajat I, Rastogi A, Singh M, Mohanty KK. Transport properties of porous media from thin-sections[C]//SPE Latin American and Caribbean Petroleum Engineering Conference, 25-28 March 2001, Buenos Aires, Argentina. DOI: http://dx.doi.org/10.2118/69623-MS.
[5] Tang T, Teng Q, He X, Luo D. A pixel selection rule based on the number of different-phase neighbours for the simulated annealing reconstruction of sandstone microstructure[J]. Journal of Microscopy, 2009, 234(3): 262-268.
[6] Zeng JB, Wu W, Jiang FM. Smoothed particle hydrodynamics prediction of effective transport coeffi cients of lithium-ion battery electrodes[J]. Solid State Ionics, 2014, 260(3): 76-85.
[7] 何绍阳, 曾建邦, 蒋方明. 锂离子电池石墨负极微结构数值重建及特征化分析[J]. 无机材料学报, 2015, 30(9): 906-912. He Shaoyang, Zeng Jianbang, Jiang Fangming. Numerical reconstruction and charactization analysis of microstructure of lithium-ion battery graphite anode[J]. Journal of Inorganic Materials, 2015, 30(9): 906-912.
[8] Lu B, Liu Q, Li GX. Grain and pore factors in acoustic response to seafl oor sediments[J]. Marine Georesources & Geotechnology, 2010, 28(2): 115-129.
[9] Jin S, Nagao J, Takeya S, Jin Y, Hayashi J, Kamata Y, et al. Structural investigation of methane hydrate sediments by microfocus X-ray computed tomography technique under high-pressure conditions[J]. Japanese Journal of Applied Physics, 2006, 45(27): 714-716.
[10] Hyodo M, Yoneda J, Yoshimoto N, Nakata Y. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed[J]. Soils and Foundations, 2013, 53(2): 299-314.
[11] Yeong CLY, Torquato S. Reconstructing random media[J]. Physical Review E, Statistical Physics, Plasmas, Fluids & Related Interdisciplinary Topics, 1998, 57(1): 495-506.
[12] Thiele S, Zengerle R, Ziegler C. Nano-morphology of a polymer electrolyte fuel cell catalyst layer-imaging, reconstruction and analysis[J]. Nano Research, 2011, 4(9): 849-860.
[13] Cheolwoong L, Bo Y, Yin LL, Zhu LK. Geometric characteristics of three dimensional reconstructed anode electrodes of lithium-ion batteries[J]. Energies, 2014, 7(4): 2558-2572.
[14] 何幼斌, 王文广. 沉积岩与沉积相[M]. 北京: 石油工业出版社, 2008. He Youbin, Wang Wenguang. Sedimentary rocks and sedimentary facies[M]. Beijing: Petroleum Industry Press, 2008.
(修改回稿日期 2016-03-08编 辑 罗冬梅)
Numerical reconstruction of 3D pore structure for gas hydrate bearing sediments
Zeng Jianbang1,2,3,4, Hu Gaowei2,3, Li Longjian4, Chen Qiang2,3, Wu Nengyou2,3, Wang Guangjun1
(1. MOE Key Laboratory of Conveyance and Equipment, East China Jiaotong University, Nanchang, Jiangxi 330013, China; 2. Qingdao Institute of Marine Geology, MLR Key Laboratory of Gas Hydrate,Qingdao, Shandong 266071, China; 3. Laboratory of Marine Mineral Resources and Detection Technologies, Qingdao National Laboratory of Marine Science and Technology, Qingdao, Shandong 266071, China; 4. MOE Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Chongqing University, Chongqing 400044, China)
NATUR. GAS IND. VOLUME 36, ISSUE 5, pp.-,5/25/2016. (ISSN 1000-0976; In Chinese)
Reconstruction of 3D pore structures is the basis and prerequisite for revealing the formation mechanisms and distribution laws of gas hydrate in sediments (hereinafter referred to as gas hydrate). Among the existing numerical reconstruction methods, the simulated annealing method is widely used. In this paper, the simulated annealing method was improved so that the actual situations could be presented better by the reconstructed structures. Important structural and statistical information could be introduced into the improved numerical reconstruction model, including the shapes of sediment particles (e.g. spherical, ellipsoidal, oblate spheroid, prolate spheroid, flakey and acicular), size distribution of sediment particles (e.g. normal distribution), and morphology of gas hydrate (e.g. cementing, floating and particle). Then, the 3D pore structures of gas hydrate bearing sediments (hereinafter referred to as sediments) were numerically reconstructed by using the improved model. Conclusions in two aspects were obtained. First, through characterization analysis on the pore structures of sediments, certain key information can be revealed, including the porosity and pore size distribution in sediments, the volume fractions of specific components and the distribution of sectional average volume fraction along x axis. Second, with the proposed numerical reconstruction model, the 3D pore structures of sediments closer to the actual situations can be reconstructed, so that the effect of gas hydrate morphology on the spatial distribution of water (or ice) and gas in the pores of sediments can be revealed.
Gas hydrate; Pore structure of sediments; Hydrate occurrence; Simulated annealing method; Numerical reconstruction; Characterization analysis
10.3787/j.issn.1000-0976.2016.05.019
国家自然科学青年基金项目(编号:51206171)、低品位能源利用技术及系统教育部重点实验室开放基金项目(编号:LLEUTS-201608)。
曾建邦,1981年生,副研究员,博士;主要从事天然气水合物成藏机理方面的研究工作。地址:(330013)江西省南昌市经济技术开发区双港东大街808号。ORCID:0000-000X-0579-5327。E-mail:jbzeng68@sina.com

