非圆特征恢复特征空间投影鲁棒波束形成

郭婷婷，徐友根＊

北京理工大学 信息与电子学院，北京 100081

非圆特征恢复特征空间投影鲁棒波束形成

郭婷婷，徐友根＊

北京理工大学 信息与电子学院，北京 100081

提出了一种利用非圆特征恢复思想的鲁棒波束形成方法。该方法在特征空间投影技术的基础上，进一步利用波束形成器输出的非圆特征参数构造代价函数，通过角度搜索使代价函数最大化来修正主瓣中心指向，在保证鲁棒性的同时尽可能提升波束形成器的输出性能。同时，该方法不需要设置用户参数，且适用于任意阶非圆信号，对于旁瓣干扰信号的非圆特性不敏感，具有广泛的应用背景。最后分别针对二阶非圆信号情形和高阶非圆信号情形进行了仿真，仿真结果验证了该方法的有效性和优越性。

鲁棒波束形成；特征空间投影；非圆特征恢复；角度搜索；高阶非圆信号

鲁棒自适应波束形成技术的主要目的是避免系统和模型误差（例如期望信号导向矢量误差、有限抽样效应等）引起的期望信号相消现象。由于鲁棒波束形成在雷达、声呐、无线通信、生物医学以及地震探测等领域都有广泛的应用［1－7］，针对各种实际场合中环境、信号和阵列模型误差的鲁棒自适应波束形成技术一直是阵列信号处理领域的研究热点［8－14］。其中，对角加载技术是得到最广泛应用的一种鲁棒自适应波束形成方法，Vorobyov、Li和Lorenz等相继提出来能够根据导向矢量不确定集的范围来选取最优参数的最差情况性能最优化（Worse－Case Performance Optimization，WCPO）［3］、鲁棒 Capon波束形成（Robust Capon Beamforming，RCB）［4］和鲁棒最小方差波束形成 （Robust Minimum Variance Beamforming，RMVB）［7］等方法。由于这些方法需要知道与期望信号导向矢量不确定集范围相关的先验知识来确定用户参数，实用性仍然值得探讨，因此研究者们开始关注无需用户参数的“全自动”对角加载鲁棒波束形成方法，如基于岭回归法（Hoerl，Kennard，and Baldwin，HKB）［8］、基于收缩运算的广义线性联合（General Linear Combination，GLC）［9］、基于功率匹配思想的半路（Midway，MW）［10］等方法。但总体而言，这些方法性能相比需用户参数的RCB、WCPO等方法较差，因此，研究性能更好的无需用户参数的全自动对角加载方法仍具有重要的研究意义。

近年来，非圆信号广泛应用在实际系统中，利用信号非圆特性的波束形成方法受到了较多的关注。实际中常用信号一般都具有Q（Q≥2）阶非圆特性，例如调幅（Amplitude Modulation，AM），二进制相移键控（Binary Phase Shift Keying，BPSK）、幅 度 键 控 （Amplitude Shift Keying，ASK）、正交振幅调制（Quadrate Amplitude Modulation，QAM）以及高斯最小频移键控（Gaussian Minimum Shift Keying，GMSK）信号等，因此利用信号非圆特征的波束形成方法具有广泛的实际应用背景，然而现有研究多集中在盲波束形成［15－16］和二阶 非 圆 信 号［17－21］。 例 如 文 献 ［21］提出了一类非圆特征恢复对角加载（Noncircularity Restoral for Diagonal Loading，NRDL）方法，该方法无需用户参数，性能较RCB、WCPO等方法更优越，但是当干扰非圆率较大时该方法性能受损。这些方法对于多进制数字相位调制（Multiple phase shift keying MPSK）、QAM 等高阶非圆信号情形不再适用，应用场合都受到一定限制。近几年，对于调制信号非圆特性的研究取得了新的进展［22－25］，非圆特征的概念扩展至高阶，相应的高阶非圆特征参数也有了严格定义［22－23］。

本文提出了一种基于任意阶（Q≥2阶）非圆信号的特征空间投影（Noncircularity Restoral Eigenspace Projection，NREP）鲁棒波束形成方法。其主要思想是先对存在误差的导向矢量向信号加干扰子空间进行投影，并将投影后获得的矢量作为估计的信号的导向矢量，进而利用角度搜索修正期望信号入射角度，能够在保证鲁棒性的同时尽可能提升波束形成器输出性能，应用背景也不再局限于BPSK、非均衡四相移键控（Unbalanced Quadrature Phase Shift Keying，UQPSK）等二阶非圆信号，而是扩展至正交相移键控（Quadrature Phase Shift Keying，QPSK）、QAM等更高阶非圆信号，因此更具实用意义。

1 问题模型

首先，介绍高阶非圆特征参数的定义。对于一个零均值复随机信号s（t），其Q阶非圆特征参数为

接着，考虑一个由N个阵元组成的均匀线阵，假设有M＋1个远场窄带信号入射至该阵列，其中第一个信号s0（t）为非圆期望信号，入射角度为θ0；其他M 个信号为任意非圆特性的干扰信号，入射角度为，则阵列的输出矢量为

式中：a（θ0）为期望信号导向矢量；a（θm）为第m 个干扰信号的导向矢量；n（t）为噪声矢量。为简单起见，一般记a（θ0）为a0，a（θm）为am。由于是均匀线阵，有

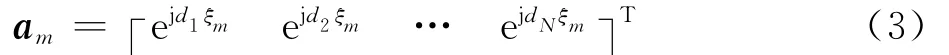
12N为阵元位置坐标。另外除非特别说明，一般假设期望信号、干扰信号、噪声均为互不相关的零均值随机过程，且假设噪声为加性（二阶）圆白噪声。

波束形成器的输出可表示为式中：w为加权向量。

2 算法原理

NREP算法是在基于特征空间投影（Eeigenspace Projection，EP）鲁棒波束形成算法的基础上提出，因此首先介绍EP算法的原理。

已知，Capon波束形成器加权向量的设计准则为

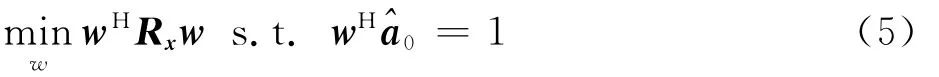
对Rx进行矩阵特征值分解可得

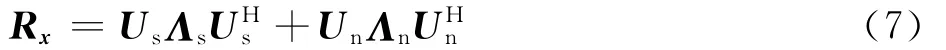
式中：Us＝［u1u2… uM＋1］，Un＝［uM＋2uM＋3… uN］，Us列向量为大特征值对应的特征矢量，张成的空间为信号加干扰子空间；Un列向量为小特征值对应的特征矢量，张成的空间为噪声子空间；Λs列向量为大特征值对应的特征值；Λn列向量为小特征值对应的特征值。将式（7）代入式（6），则Capon的最优权矢量可写为

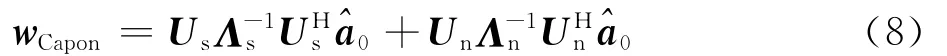
为了消除导向矢量失配引起的一系列问题，将存在误差的导向矢量向信号加干扰子空间进行投影，将投影后获得的矢量作为估计的信号的导向矢量。定义投影后的导向矢量为

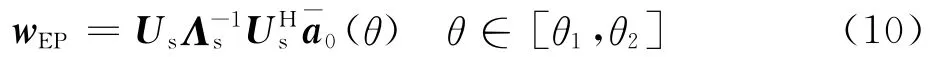
至此，即可获得EP算法的最优加权矢量为式中：［θ1，θ2］为包含期望信号实际方向θ0在内的一个角度区域，需满足干扰方向θm［θ1，θ2］，m＝1，2，…，M，［θ1，θ2］的区域范围可利用期望信号标称方位角（与θ0之间存在误差）来确定，例如令可通过实际系统的等效指向误差范围来确定。

接着，考虑利用非圆特征恢复的思想确定期望信号方位角，利用使波束形成器输出非圆率尽可能地接近期望信号的非圆率准则来建立代价函数，有

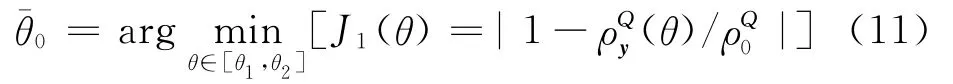
再根据式（1），可以得到式（12）中Q 阶非圆参数的估计为

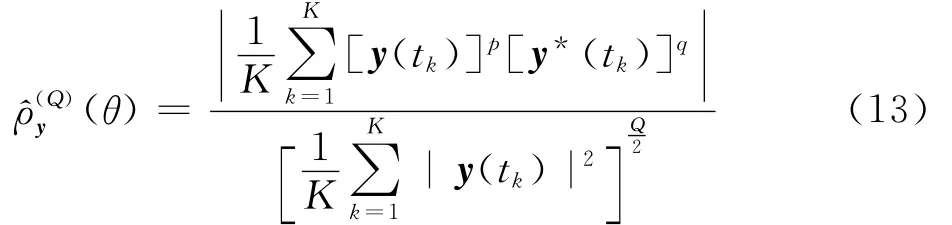
式中：

由式（12）求得珋θ0后，代入式（10），可得NREP方法的最优权矢量为

3 仿真分析

考虑一个阵元间距为信号半波长的均匀线阵，阵元数为10，期望信号入射角的标称值为0°，干扰信号入射方向分别为30°和－40°，信干比（SINR）为－20dB。

实验1 期望信号为二阶非圆信号时，波束形成器输出信干噪比（Output Signal to Interference plus Noise Ratio，OSINR）性能比较。

令期望信号非圆率为1，干扰信号非圆率分别为1和0。假设期望信号实际入射角度为5°（指向误差为5°），角度搜索区域均为［－5°，5°］（Δθ＝5°），搜索步进为0．2°，固定快拍数（Snapshot Number）为100，波束形成器的输出信干噪比随输入干信噪比（Input Signal to Interference plus Noise Ratio，ISINR）变化趋势如图1（a）所示；固定信噪比为20dB，波束形成器输出信干噪比随快拍数变化趋势如图1（b）所示。

图1 ρ0＝1、ρ1＝1和ρ2＝0时输出信干噪比（OSINR）性能变化曲线Fig．1 Output signal to interference plus noise ratio（OSINR）comparison whenρ0＝1，ρ1＝1，ρ2＝0

实验2 期望信号为高阶非圆信号时，波束形成器输出信干噪比性能比较。

首先，令期望和干扰信号均为QPSK信号，其余条件同上。波束形成器的输出信干噪比随输入信噪比变化趋势如图2（a）所示；波束形成器输出信干噪比随快拍数变化趋势如图2（b）所示。

然后，令期望信号为QPSK信号，干扰信号分别为QPSK信号和BPSK信号。波束形成器的输出信干噪比随输入信噪比变化趋势如图3（a）所示；波束形成器输出信干噪比随快拍数变化趋势如图3（b）所示。

最后，令期望信号二阶非圆率为0．5，干扰信号二阶非圆率分别为1和0。波束形成器的输出信干噪比随输入信噪比变化趋势如图4（a）所示；波束形成器输出信干噪比随快拍数变化趋势如图4（b）所示。

图2 ρ0＝ρ1＝ρ2＝0时OSINR性能变化曲线Fig．2 OSINR comparison whenρ0＝ρ1＝ρ2＝0

图3 ρ0＝0、ρ1＝0和ρ2＝1时OSINR性能变化曲线Fig．3 OSINR comparison whenρ0＝0，ρ1＝0，ρ2＝1

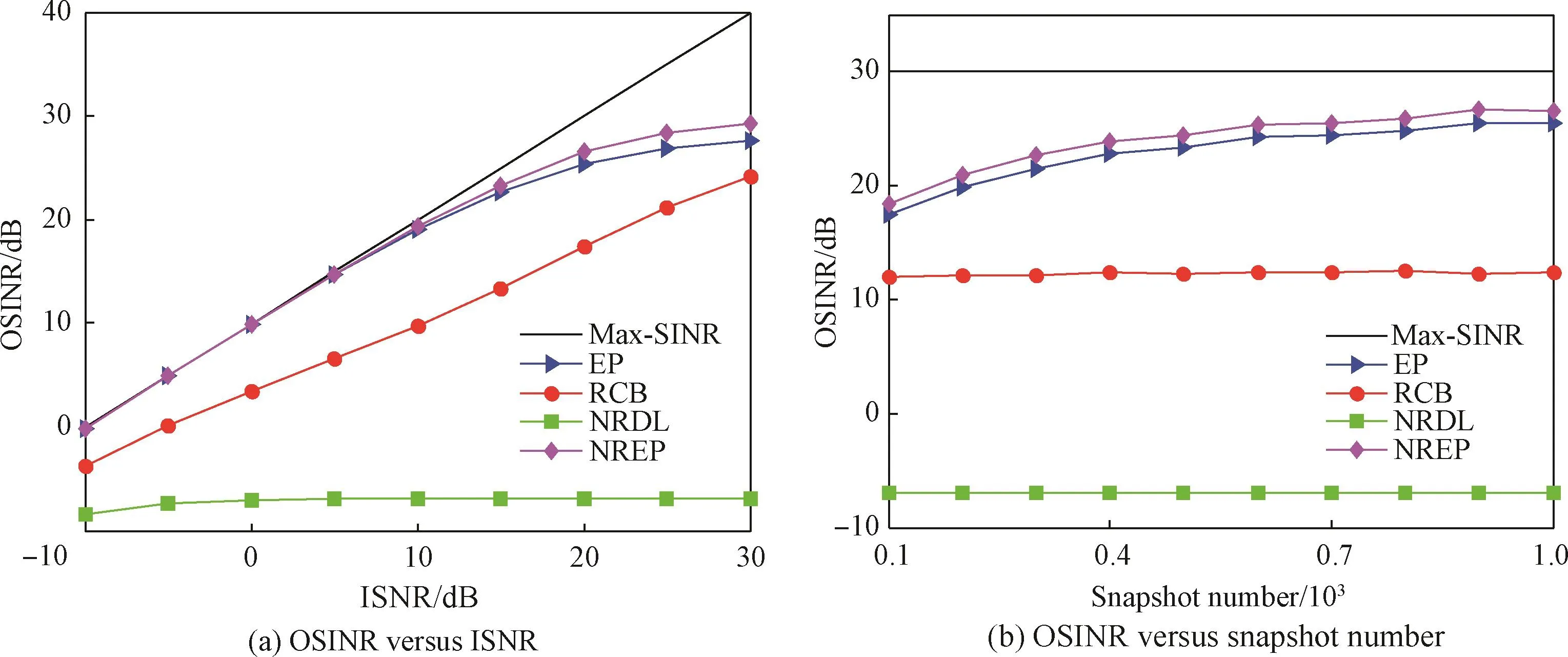
图4 ρ0＝0．5、ρ1＝1和ρ2＝0时OSINR性能变化曲线Fig．4 OSINR comparison whenρ0＝0．5，ρ1＝1，ρ2＝0

综上仿真结果表明，NREP方法相对RCB、NRDL等方法在二阶非圆和高阶非圆条件下都有明显的性能优势，同时波束形成器的输出性能对干扰的非圆特性不敏感。

4 结 论

1）本文提出的NREP方法与NRDL、RCB等方法相比，虽然都能应用于高阶非圆信号，但输出性能优势显著。

2）与仅利用期望信号二阶非圆特性的波束形成方法相比，NREP可有效应用于高阶非圆信号，且对于旁瓣干扰信号的非圆特性不敏感，具有更加广泛的应用前景。

3）与EP方法相比，输出性能的提升是由于利用非圆特征恢复准则提高了期望信号导向矢量的可靠性，更好地解决了指向误差所带来的影响，因此对于期望信号存在较大指向误差的场合，NREP方法会有更明显的性能优势。

4）由于需利用高阶统计信息，需较大采样数保证统计信息的准确性，因此NREP方法更适用于采样数和指向误差较大的环境。

［1］ GERSHMAN A B．Robust adaptive beamforming in sensor arrays［J］．International Journal of Electronics and Communications，1999，53（6）：305－314．

［2］ GERSHMAN A B．Robust adaptive beamforming：An overview of recent trends and advances in the field ［C］／Proceedings of International Conference on Antenna Theory and Techniques，2003：30－35．

［3］ VOROBYOV S A，GERSHMAN A B，LUO Z Q．Robust adaptive beamforming using worst－case performance optimization：A solution to the signal mismatch problem ［J］．IEEE Transactions on Signal Processing，2003，51（2）：313－324．

［4］ LI J，STOICA P，WANG Z S．On robust Capon beamforming and diagonal loading［J］．IEEE Transactions on Signal Processing，2003，51（7）：1702－1715．

［5］ LORENZ R G，BOYD S P．Robust beamforming in GPS arrays［C］／Proceedings of the Institute of Navigation，2001：409－427．

［6］ LORENZ R G，BOYD S P．Robust minimum variance beamforming［C］／37th Asilomar Conference on Signals，Systems，and Computers，2003：1345－1352．

［7］ LORENZ R G，BOYD S P．Robust minimum variance beamforming［J］．IEEE Transactions on Signal Processing，2005，53（5）：1684－1696．

［8］ SENLEN Y，ABRAHAMSSON R，STOICA P．Automatic robust adaptive beamforming via ridge regression［J］．Signal Processing，2007，2（1）：33－49．

［9］ DU L，STOICA P．Fully automatic computation of diagonal loading levels for robust adaptive beamforming ［J］．IEEE Transactions on Aerospace and Electronic Systems，2010，46（1）：449－458．

［10］ STOICA P，LI J，TAN X．On spatial power spectrum and signal estimation using the Pisarenko framework ［J］．IEEE Transactions on Signal Processing，2008，56（10）：5109－5119．

［11］ ARASH K，VOROBYOV S A，HASSANIEN A．Robust adaptive beamforming based on steering vector estimation with as little as possible prior information ［J］．IEEE Transactions on Signal Processing，2012，60 （6）：2974－2987．

［12］ GU Y，LESHEM A．Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation ［J］．IEEE Transactions on Signal Processing，2012，60（7）：3881－3885．

［13］ JIA W M，JIN W，ZHOU S H，et al．Robust adaptive beamforming based on a new steering vector estimation algorithm ［J］．Signal Processing，2013，93（9）：2539－2542．

［14］ GU Y J，GOODMAN N A，HONG S H，et al．Robust adaptive beamforming based on interference covariance matrix sparse resconstruction ［J］．Signal Processing，2014，96（5）：375－381．

［15］ GALY J，ADNET C．Blind separation of non－circular sources［C］／Proceedings of 10th IEEE Workshop on Statistical Signal and Array Processing．Piscataway，NJ：IEEE Press，2000：315－318．

［16］ XU Y G，LIU Z W．Noncircularity restoral for multi－antenna adaptive blind beamforming ［J］．Multidimensional Systems and Signal Processing，2010，21（2）：133－160．

［17］ CHEVALIER P，BLIN A．Widely linear MVDR beamformers for the reception of an unknown signal corrupted by noncircular interferences［J］．IEEE Transactions on Signal Processing，2007，55（11）：5323－5336．

［18］ WANG G H，LIE J P，SEE C－M S．A robust approach to optimum widely linear MVDR beamformer［C］／Proceedings of IEEE Conference on Acoustics，Speech and Signal Processing （ICASSP）．Piscataway，NJ：IEEE Press，2012：2593－2596．

［19］ STEINWANDT J，HAARDT M．Optimal widely－linear distributed beamforming for relay networks［C］／Proceedings of IEEE Conference on Acoustics，Speech and Signal Processing （ICASSP）．Piscataway，NJ：IEEE Press，2013：4215－4241．

［20］ XU D Y，HUANG L，XU X，et al．Widely linear MVDR beamformers for noncircular signals based on time－averaged second－order noncircularity coefficient estimation［J］．IEEE Transactions on Vehicular Technology，2013，62（7）：3219－3227．

［21］ XU Y G，MA J Y，LIU Z W，et al．A class of diagonally loaded robust capon beamformers for noncircular signals of interest［J］．Signal Processing，2014，94（1）：670－680．

［22］ ERIKSSON J，OLLILA E，KOIVUNEN V．Essential statistics and tools for complex random variables ［J］．IEEE Transactions on Signal Processing，2010，58（10）：5400－5408．

［23］ OLLILA E，ERIKSSON J，KOIVUNEN V．Complex elliptically symmetric random variables—generation，characterization，and circularity test［J］．IEEE Transactions on Signal Processing，2011，59（1）：58－69．

［24］ RYTEL－ANDRIANIK R．On circularity of complex－valued radar signals ［C］／Signal Processing Symposium，2013：1－6．

［25］ 马静艳．利用信号非圆特征的鲁棒波束形成算法研究［D］．北京：北京理工大学，2014：76－87．MA J Y．Noncircularity exploitation in roubst adaptive beamforming［D］．Beijing：Beijing Institute of Technology，2014：76－87（in Chinese）．

Noncircularity restoral eigenspace projection robust beamforming

GUO Tingting，XU Yougen＊
School of Information and Electronics，Beijing Institute of Technology，Beijing 100081，China

A new robust beamformer exploiting noncircularity restoral of desired signal is proposed．The new approach is based on the eigenspace projection，further uses the noncircularity coefficient of the beamformer output to construct the cost function and modifies the pointing direction of the main beam via azimuth searching to maximize the noncircularity coefficient of the beamformer output，so that it could improve the output performance of beamformer while the robustness is guaranteed．The new method doesn’t need to set user parameters，and it is applicable for the Qth（Q≥2）order noncircular modulated signal．At the same time，the new method is not sensitive to the noncircularity of the sidelobe interference signal，which is widely used in practice．At the end of this paper，the simulations for the case of second order noncircular signal and the case of high order noncircular signal were carried out，and the results verify the validity and superiority of the proposed approach．

robust beamforming；eigenspace projection；noncircularity restoral；azimuth searching；high－order noncircular signal

2015－10－12；Revised：2015－11－19；Accepted：2015－12－31；Published online：2016－01－06 15：55

URL：www．cnki．net／kcms／detail／11．1929．V．20160106．1555．010．html

s：National Natural Science Foundation of China（61331019，61490691）

V219；TN911．7

A

1000－6893（2016）09－2833－06

10．7527／S1000－6893．2015．0366

2015－10－12；退修日期：2015－11－19；录用日期：2015－12－31；网络出版时间：2016－01－06 15：55

www．cnki．net／kcms／detail／11．1929．V．20160106．1555．010．html

国家自然科学基金 （61331019，61490691）

＊通讯作者．Tel．：010－68912606 E－mail：yougenxu＠bit．edu．cn

郭婷婷，徐友根．非圆特征恢复特征空间投影鲁棒波束形成［J］．航空学报，2016，37（9）：28332－838．GUOT T ，XUY G ．Noncircularity restoral eigenspace projection robust beamforming［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：28332－838．

郭婷婷 女，硕士。主要研究方向：阵列信号处理。Tel：010－68912606

E－mail：gtt＿2016＠163．com

徐友根 男，博士，副教授，博士生导师。主要研究方向：阵列信号处理。

Tel：010－68912606

E－mail：yougenxu＠bit．edu．cn

＊Corresponding author．Tel．：010－68912606 E－mail：yougenxu＠bit．edu．cn