薄壁钛管剪应力本构参数识别方法

闫晶＊，吴为

1．塑性成形技术航空科技重点实验室，北京 100024 2．数字化塑性成形技术及装备北京市重点实验室，北京 100024 3．北京航空制造工程研究所，北京 100024

薄壁钛管剪应力本构参数识别方法

闫晶1，2，3，＊，吴为1，2，3

1．塑性成形技术航空科技重点实验室，北京 100024 2．数字化塑性成形技术及装备北京市重点实验室，北京 100024 3．北京航空制造工程研究所，北京 100024

不同温度下的薄壁钛管剪应力本构参数识别，是研究薄壁钛管差温剪切弯曲过程管材塑性变形行为迫切需要解决的关键问题。提出了一种管材剪切测试的方法。将不同温度下薄壁钛管等温剪切测试、剪切测试过程模拟有限元模型、以及基于距离函数的响应面模型相结合，提出了薄壁钛管不同温度下剪应力本构参数逆向识别方法。采用该方法，识别了TA2薄壁钛管剪应力本构参数。同时建立了TA2薄壁钛管差温剪切弯曲过程模拟3维弹塑性热力耦合有限元模型。分别采用剪应力本构参数和单拉应力本构参数模拟弯管实验过程，评估了有限元模型的可靠性。结果表明：对于剪应力本构参数，温度越高，管材的K值和n值将减小，m值呈现波动的趋势。与单拉应力本构参数相比，剪应力本构参数对温度的变化更敏感，且剪应力本构参数值较小。与单拉应力本构参数相比，使用剪应力本构参数的有限元模型精度较高，模拟精度最大提高了60%。

薄壁钛管；本构参数；剪应力；参数识别；有限元

管材弯曲成形技术，是制造管形构件的关键技术，极小弯曲半径（中心线弯曲半径小于管直径）弯管技术已成为管材弯曲成形技术的发展趋势［1］。与传统的 管 材 绕 弯 成 形 技 术［2－5］和 推 弯 成形技术［6］相比，薄壁钛管差温剪切弯曲成形技术（见图1），结合了管材剪切弯曲成形技术和材料差温控制的优势，具有省力和提升难变形材料成形性的优点，为极小弯曲半径薄壁钛管的成形提供了一种新的技术思路。管材在剪力的作用下发生弯曲变形，管材承受较大的剪应力，弯曲变形伴随着明显的剪切变形。因此，不同温度下的薄壁钛管剪应力本构参数，是开展薄壁钛管差温剪切弯曲成形技术研究，迫切需要解决的重要基础问题。

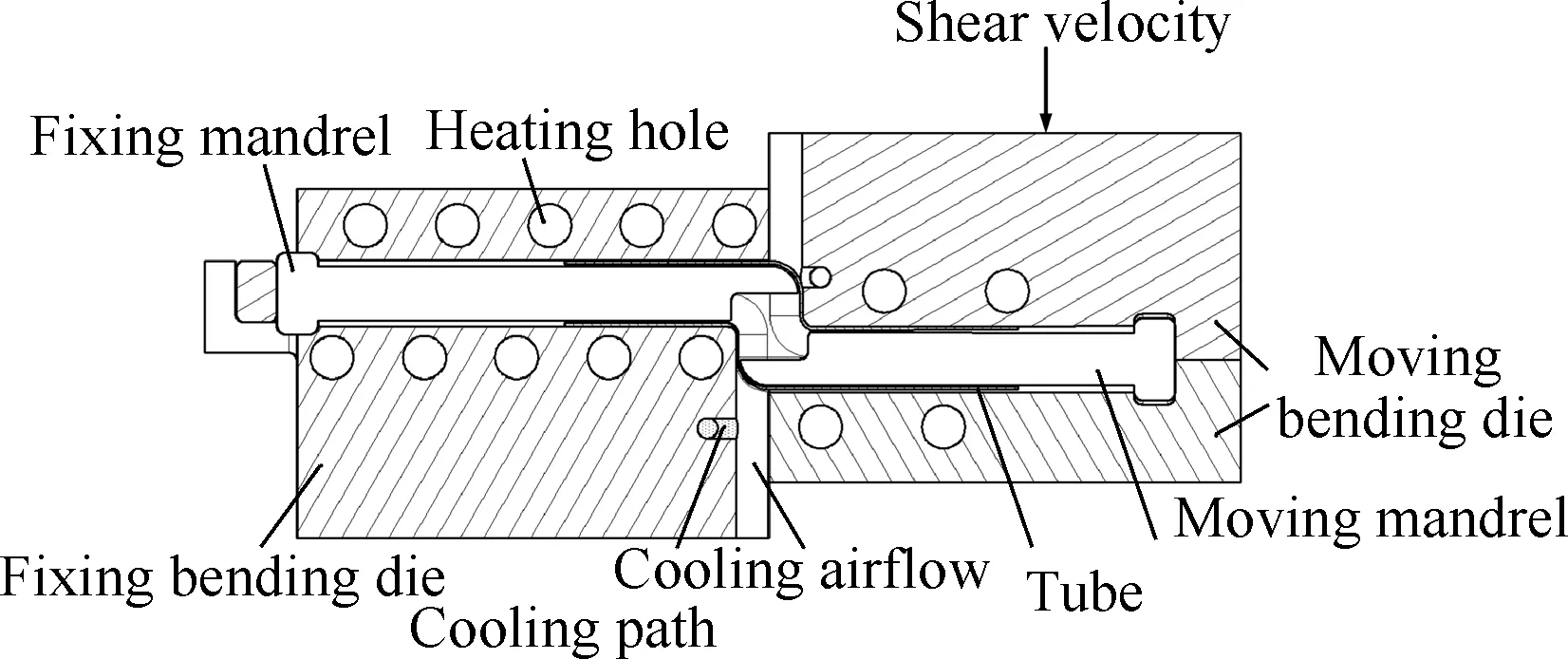
图1 管材差温剪切弯曲示意图Fig．1 Schematic diagram of tube shear bending process under differential temperature fields constraints（DTFCs）

有限元数值模拟是研究薄壁钛管差温剪切弯曲过程的一个重要方法，不同温度下管材塑性本构参数数值模拟精度的关键因素之一。然而，目前可供工程设计使用的薄壁钛管本构参数，多数是基于不同温度下恒应变速率单拉测试获得，本构参数仅能反映单拉应力状态［7－9］，难以有效反映管材差温剪切弯曲过程材料的剪切变形行为。

几十年来，针对板／管金属剪应力本构参数的识别，国内外学者开展了大量的研究工作，研究方法是基于板／管剪切测试实验，采用光学应变测量装置测量材料剪切变形，进而获得材料的剪应力－应变曲线，并将之转换为等效应力－应变曲线，最终识别出材料的本构参数［10－15］。按照测试试样结构，板材剪切测试方法主要包括：循环双沟槽剪切测试［13］、单 边 剪 切 测 试［16］，Miyauchi剪 切 测试［17］，以 及 ASTM B831－05 标 准 剪 切 测 试［18］。管材剪切测试方法主要包括两种，即管材简单剪切测试和管材扭转测试［19］，管材剪切测试夹具结构复杂，而且需要专用设备。上述本构参数识别方法的关键是准确在线测量材料的剪切变形，需要专用光学在线检测系统，测试成本较高。到目前为止，国内外针对板／管剪应力本构参数的识别研究主 要 针 对 室 温 条 件 下 的 测 试 过 程［10－14，15－20］，对于热态测试过程的研究仍然较薄弱，热变形测试过程恒应变速率的控制难度较大，难以获得材料的本构参数［15］。此外，热变形条件下的管材剪应力本构参数的逆向识别的研究仍罕见报道。

板／管本构参数的逆向识别方法，是基于数值模拟或理论解析和测试相结合的反算法确定材料本构参数，该法将参数的识别归结为一个非线性优化问题。其中，建立材料本构参数与剪切测试结果间的非线性方程并优化，是该方法的关键。目前，国内外学者主要采用理论解析、回归分析和人工神经网络建立上述非线性方程［20－23］。理论解析的方法难以全面考虑本构参数间的交互作用［20－22］；人工神经网络的方法能够实现识别材料参数与实验结果间的非线性逼近，但是却不能给出非线性方程的显式表达式，不利于识别结果的进一步优化［23］。建立材料本构参数与剪切测试结果的定量关系，需要付出较大的计算成本。将成形过程模拟有限元模型和响应面法相结合，构筑成形过程工艺参数与成形指标间的多项式模型，具有高效准确的优点，已被广泛地应用于钣金成形工艺设计中［24－26］。

因此，在修改的ASTM B831－05标准剪切管材试样基础上，本文提出了一种管材剪切测试的方法。将不同温度下薄壁钛管等温剪切测试、剪切测试过程模拟有限元模型、以及基于距离函数的响应面模型相结合，提出了薄壁钛管剪应力本构参数逆向识别方法。该方法不需要直接测量材料的剪切变形，测试过程成本低廉，可靠性较高。采用该方法，获得了不同温度下的TA2薄壁钛管剪应力本构参数，同时，建立了TA2薄壁钛管差温剪切弯曲过程模拟3维弹塑性热力耦合有限元模型，分别采用剪应力本构参数和单拉应力本构参数模拟实验过程，评估本构参数对有限元模型计算精度的影响。

1 研究方法

1．1 管材剪应力本构参数识别方法

1．1．1 管材剪切测试

在修改的ASTM B831－05标准剪切试样的基础上［7］，针对管材几何尺寸的特点，针对直径32mm，壁厚1．5mm的TA2钛管，设计制造了管材剪切试样及夹具（见图2），其中在管材试样内外表面增加镶块，镶块与管材试样采用销钉连接固定，保证剪切测试过程管材与镶块的接触区域为刚性区。

图2 管材剪切测试试样及夹具Fig．2 Tube specimen and clamping dies of shear test

对于TA2钛合金，传统热成形温度范围为500～600℃，温度越高，零件氧化越严重，同时，材料晶粒度也会增加。在保证材料变形抗力在一定程度降低的同时，尽可能地选择较低的成形温度，将有利于材料性能的控制［27］。因此本文选择TA2钛管剪切测试的温度范围为25、300、350、400、450和500℃，分别在不同温度下开展等温剪切测试，实验在材料单拉测试设备上开展，将试样与单拉实验机上下夹头相连，测试过程中夹头保持0．02 mm／s恒速拉伸，对试样施加轴向载荷，进而试样沟槽衔接区域产生剪应力，发生剪切变形，测试过程在线记录轴向载荷和夹头位移的关系曲线。

由不同温度下的管材剪切测试后的试样（见图3）可知，剪切测试过程中管材与镶块接触区域的绝大部分为刚性传力区，管材试样的变形区为没有与镶块接触的管材试样区域。图4为不同温度下管材剪切测试的力－位移曲线，F表示力，l′表示位移，可以发现，曲线记录了剪切测试前期力随位移的变化情况，能够反映不同温度下管材的均匀剪切变形。此外，在等温条件下，载荷随位移的增加均表现出一定的强化趋势；随着温度的升高，曲线的剪切载荷越低。因此，该曲线可以用来

图3 管材剪切测试后的试样Fig．3 Tube specimens after shear tests

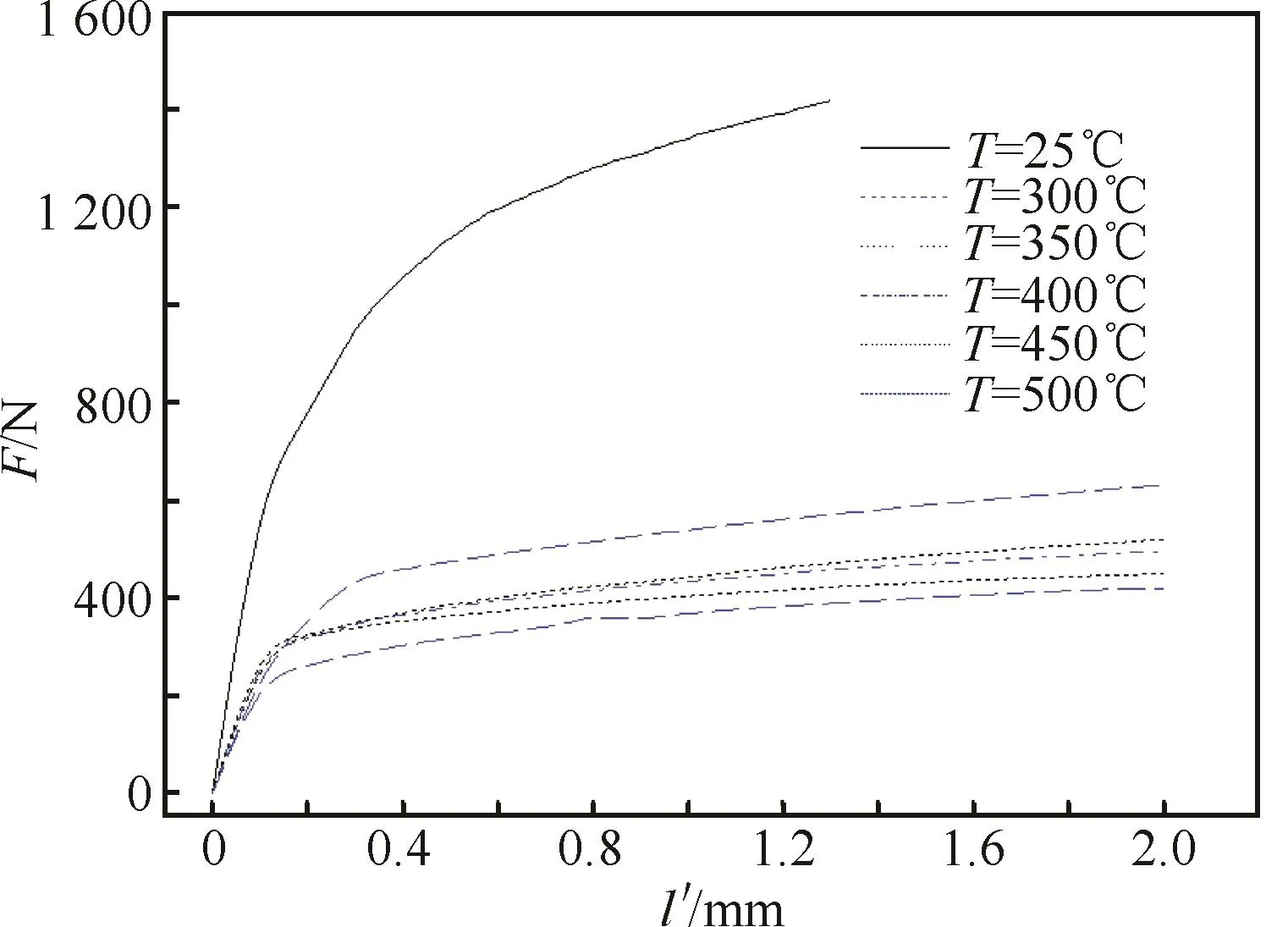
图4 管材剪切测试力－位移曲线Fig．4 Load－displacement curves of tube shear tests

识别不同温度下的管材本构方程，管材本构关系可以用25℃下的材料本构方程式（1）和300、350、400、450和500℃等温剪切测试过程的材料本构方程式（2）描述：式中：ε为等效应变；σ为等效应力；K为强度系数；n为应变硬化指数；m为应变速率敏感系数，它们均为温度T的函数。

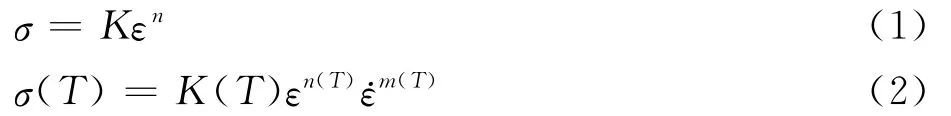
1．1．2 管材剪切测试有限元模型

基于ABAQUS软件环境下的静力隐式有限元算法，建立了TA2钛管等温剪切测试过程模拟有限元模型。图5是具有代表性的等温剪切测试过程模拟有限元模型，其中，S为等效应力。根据管材剪切测试实验过程，将管材试样划分为2个区域，管材与镶块接触的区域为刚性区，采用刚体约束，单元在计算过程中不发生变形，管材没有与镶块接触的区域为变形区，采用4节点有限薄膜应变减缩积分双曲壳单元离散，剪切变形区的平均单元尺寸为0．1mm。

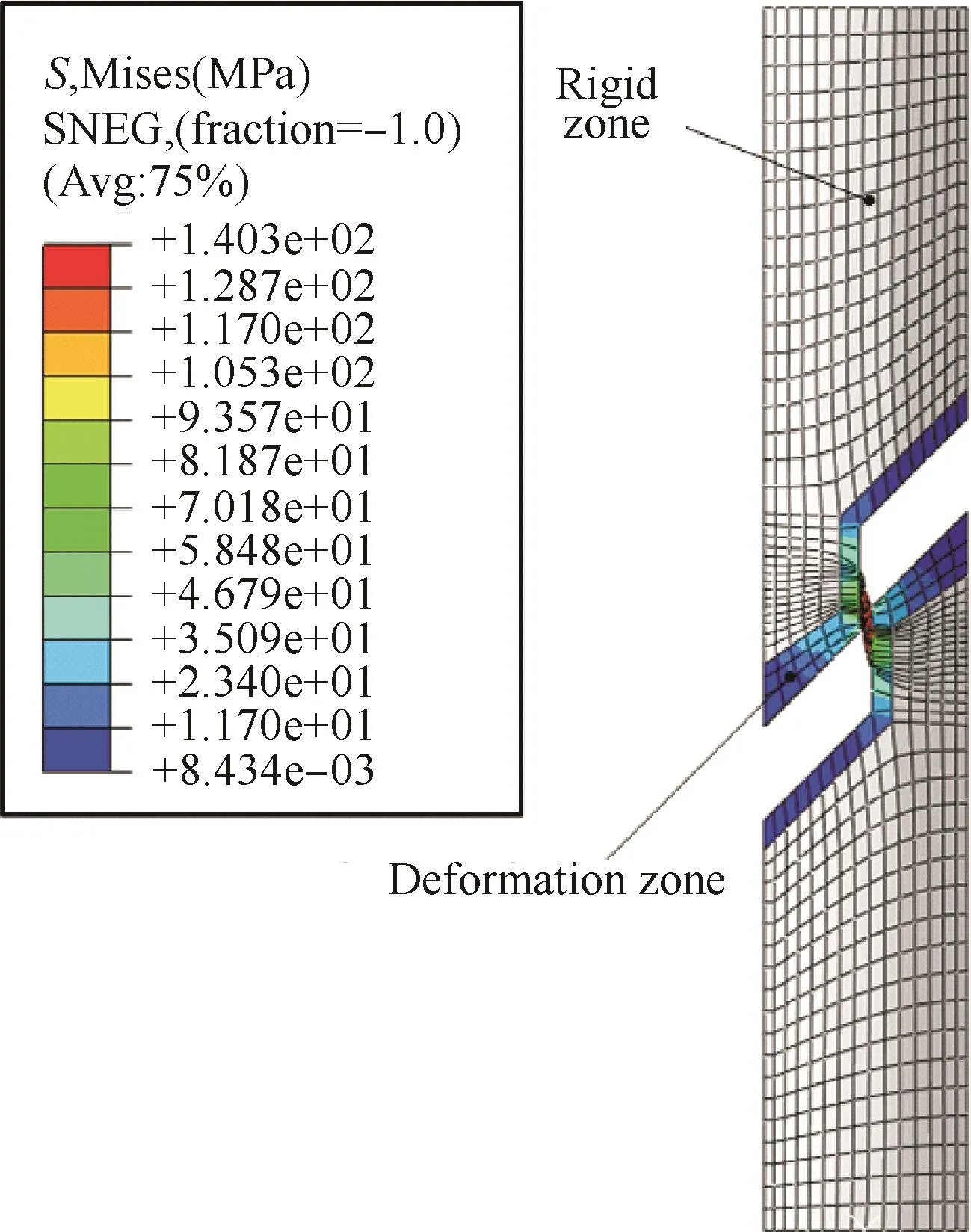
图5 具有代表性的管材等温剪切测试模拟有限元模型Fig．5 A representative finite element model for simulating isothermal tube shear test

管材假设为各向同性材料，管材塑性屈服遵守Mises屈服准则，弹性模量随温度的变化如表1所示。本构方程如式（1）和式（2）所示。

设定下刚性区所有方向的位移为0mm。对上刚性区，仅沿管材轴线方向施加拉伸速度，实现剪切加载，速度与实验过程一致为0．02mm／s。加载时间大于320s。

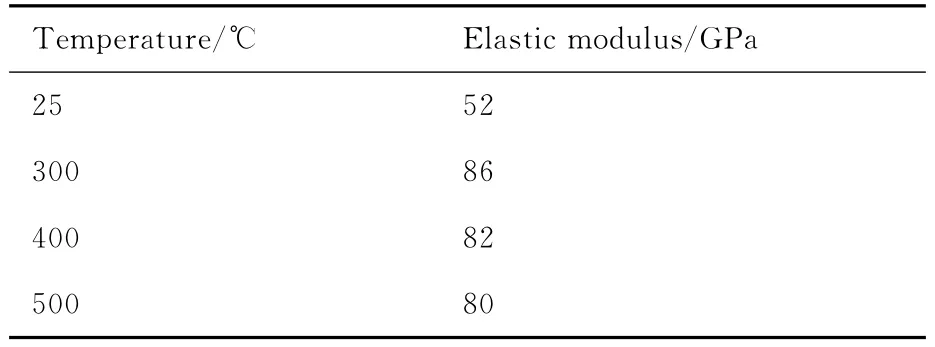
表1 TA2薄壁钛管弹性模量［28］Table 1 Elastic modulus of TA2titanium alloy thin－walled tube［28］

1．1．3 基于距离函数的响应面模型

1．1．3．1 距离函数

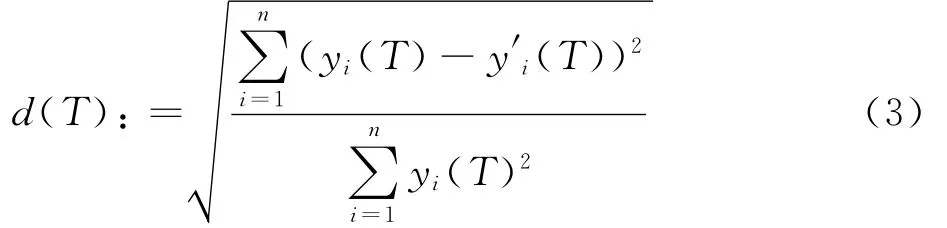
采用距离函数描述不同的力－位移曲线间的距离，其表达式为式中：d（T）：为距离函数；yi（T）为温度T 下的等温剪切测试的载荷点；y′i（T）为剪切测试过程模拟有限元模型的计算结果，是（K（T），n（T），m（T））的函数，即

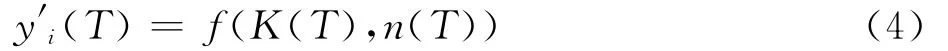
或

因此，

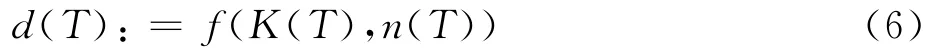
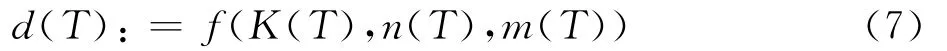
或其中：式（4）和式（5）可以由剪切测试过程模拟有限元模型计算确定，进而可以确定式（6）和式（7）。

1．1．3．2 响应面模型

采用响应面法确定式（6）和式（7），并建立d（T）：的多项式回归模型，即通过组合设计N个实验数据求得d（T）：的二次回归方程［29］

式中：β0（T）、βj（T）、βhj（T）和βjj（T）分别为方程的常数项、线性项、交互项以及2次项的回归系数；xj（T）为材料本构参数；j为本构参数的个数。实验次数为

式中：第1项表征各本构参数皆取2水平（＋1，－1）的全面实验数；第2项表征第j个本构参数取常数水平，其他j－1个本构参数取0水平，进行实验的点数；第3项表征各本构参数均取0水平的实验数。

1．1．4 参数逆向识别方法

图6为基于剪应力的材料本构参数识别方法，该方法将不同温度下管材等温剪切测试、等温剪切测试过程模拟有限元模型以及响应面法相结合，在不同温度条件下，构建距离函数与材料本构参数之间的响应面模型，将本构参数识别问题归结为求最小距离函数的问题，即找到（K（T），n（T），m（T））＞0，使得

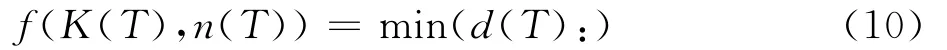
或

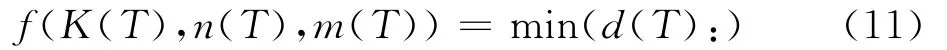
最终获得不同温度条件下基于剪应力的材料本构参数（K（T），n（T），m（T））。

1．2 管材差温剪切弯曲有限元模型

基于ABAQUS软件平台的动力显式热力耦合分析模块，建立了TA2薄壁钛管差温剪切弯曲过程模拟3维弹塑性热力耦合有限元模型，图7为该过程具有代表性的有限元模型。考虑管材和成形模具的几何对称性，仅按管材和成形模具的一半建模。管材为变形体，采用1mm×1mm热力耦合8节点4边形减缩积分双曲壳元离散；将模具的几何结构简化为模具型腔壳体，采用热力耦合8节点4边形双曲壳元离散，同时对模具施加刚体约束，实现模具刚性化。

根据管材差温剪切弯曲过程模具的相对运动形式，定义定弯曲模和定芯模的沿各方向的位移为0mm，对动弯曲模和动芯模沿着Y方向施加一定的剪切速度，定义其他方向的速度为0mm／s。定义管材分半对称面沿Z方向的位移为0mm，其他方向的位移不受约束。

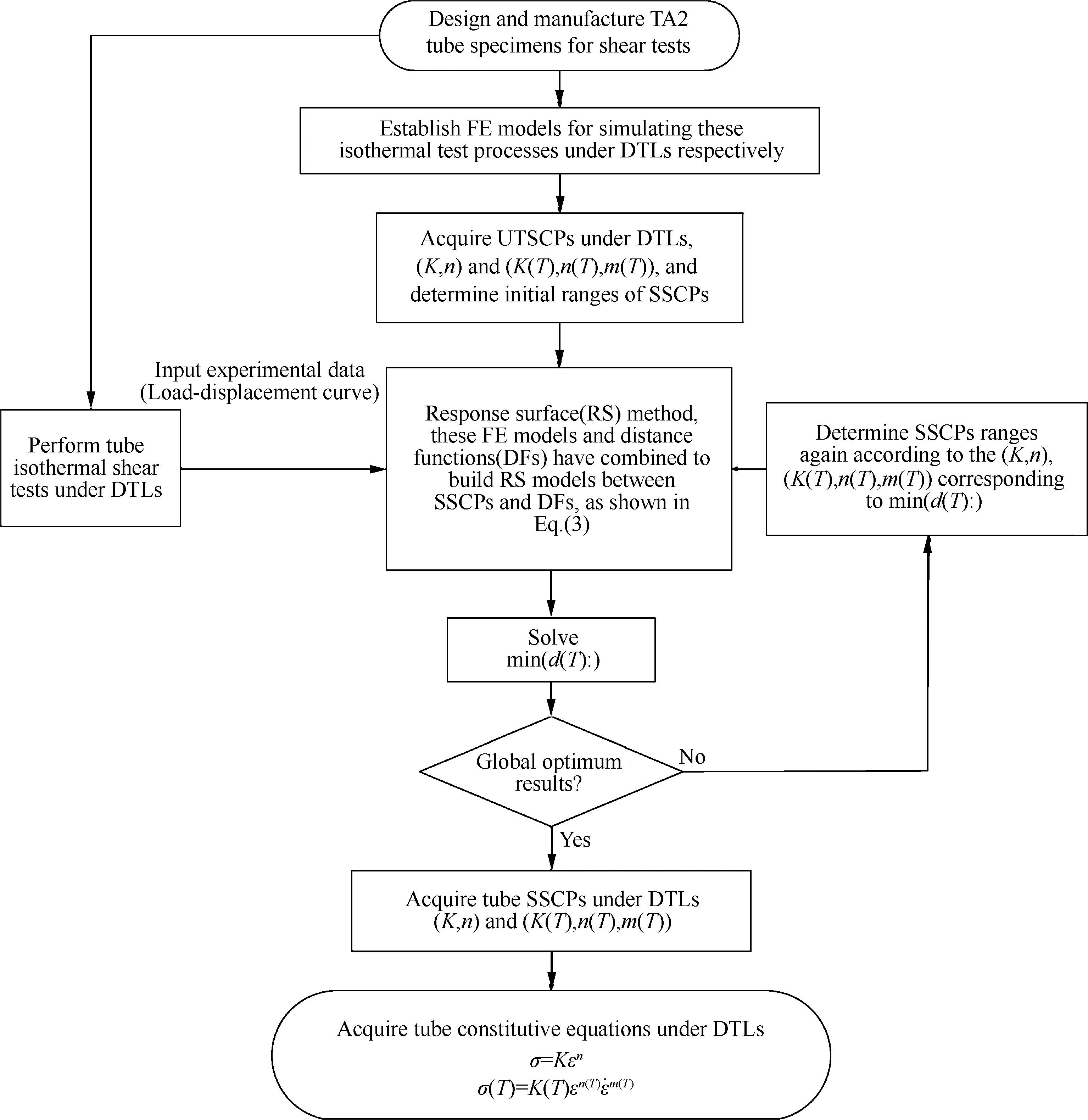
图6 剪应力本构参数识别方法Fig．6 Identification method of constitutive parameters based on shear stress

图7 具有代表性的管材差温剪切弯曲模拟有限元模型Fig．7 A typical FE model for simulating tube shear bending process under DTFCs

分别定义管材内表面与芯模接触、管材外表面与弯曲模接触，采用接触对算法模拟管模间的接触，管模间的法向接触行为为硬接触，切向接触行为采用库仑摩擦模型［30］描述。管模间的滑动计算采用有限滑动算法模拟。在管模接触定义中，考虑了管模间的摩擦产热。

按照管材成形温度，定义了管材和模具的初始温度场，且温度场分布均匀，同时不考虑模具的热阻。弯管过程中，分别定义了管材、模具与周围环境间的对流换热、辐射换热，以及管材与模具间的间隙热传导，实现弯管过程管材温度变化的模拟。其中，对流换热采用定义“对流换热系数”和“温度差”的方式实现，辐射换热采用定义“辐射系数”和“温度差”的方式实现。

假设TA2钛管为各向同性材料，满足Mises屈服准则，有限元模型材料属性定义了管材的弹性模量、质量热容、热导率随温度的变化，具体参数值见文献［31］。分别采用单拉应力本构参数，和剪应力本构参数，模拟TA2钛管差温剪切弯曲实验过程，按图8的测量轨迹，测量管材厚向应变分布，并与实验结果对比。有限元模拟参数与实验参数相同，如表2所示。

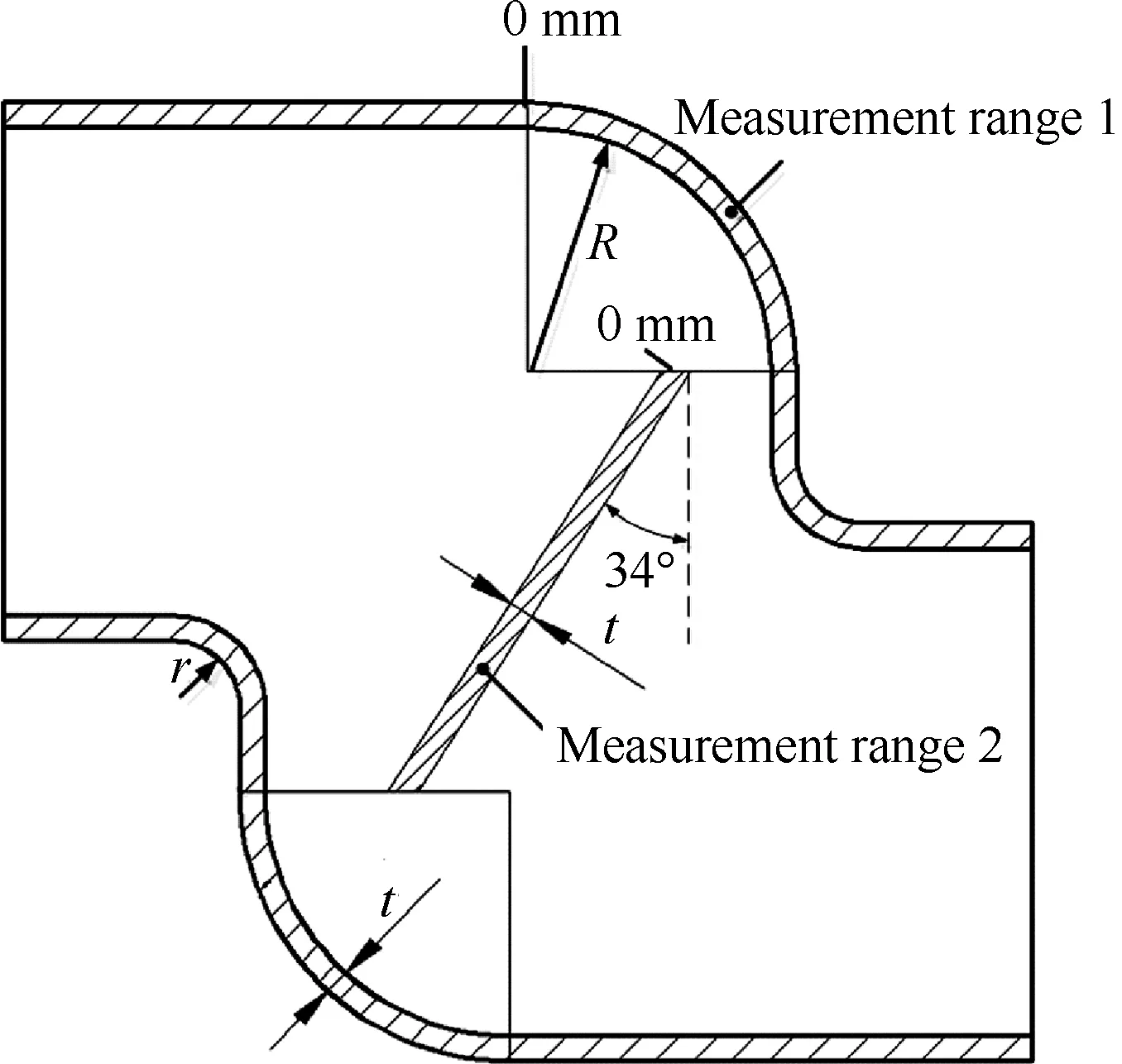
图8 管件测量区间Fig．8 Measurement range of a tube part

2 结果与讨论

2．1 管材单拉应力本构参数

针对相同规格的TA2薄壁钛管，依据GB／T4338－2006，开展热变形恒应变速率单拉测试。管材试样采用线切割沿管材表面加工。在300、350、400、450和500℃温度范围内，针对每个温度点，分别在不同恒应变速率0．05、0．01、0．005s－1条件下，采用高温引伸计测量管材应力应变曲线。每次实验重复2次。

采用本构参数正向识别方法［32］，获得了管材单拉应力本构参数与温度倒数的关系，如图9所示。可以发现，随着T的增加，n先增加再减小，n值最大相对变化量为15%；当T＝400℃时，n值最大。T越高，m值越大，m值最大相对变化量为33%；同时K值越小，K值最大相对变化量为26%。管材单拉应力本构参数为

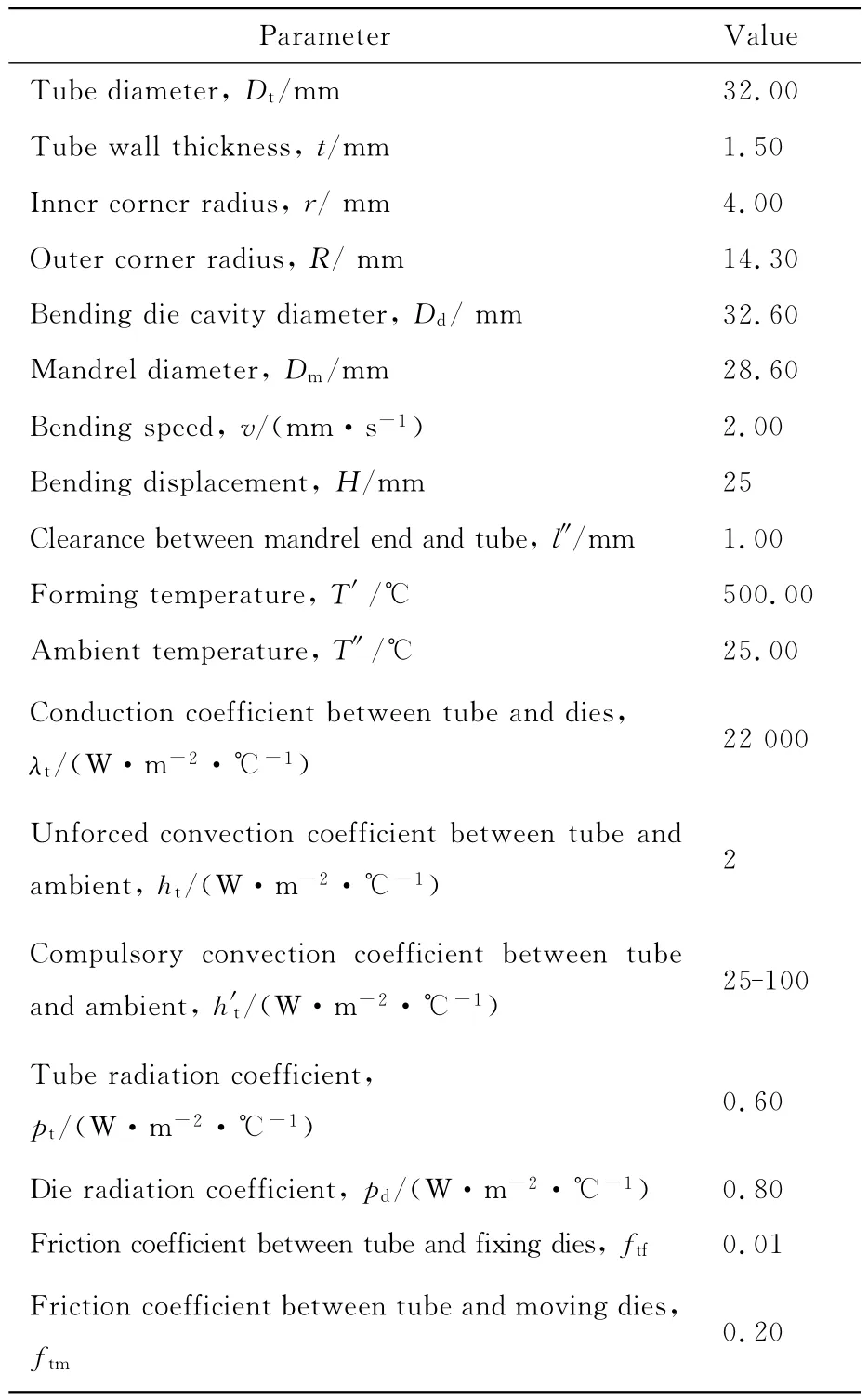
表2 有限元模型模拟参数Table 2 Simulation parameters of FE model

图10为不同温度下管材的真实应力－应变曲线，可以发现采用单拉应力本构参数计算的真应力－应变曲线，与实验测试的结果非常接近。因此，获得的单拉应力本构参数是可靠的。

2．2 管材剪应力本构参数

2．2．1 响应面模型

由于不同温度下管材剪切测试过程“力－位移”曲线是不同的，因此，与每根“力－位移”曲线对应的本构参数与距离函数的响应面模型也是不同的，

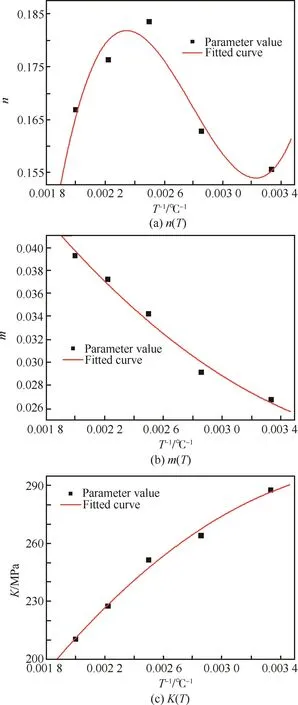
图9 单拉应力本构参数与温度的关系Fig．9 Relationships between constitutive parameters based on uniaxial tension stresses and temperatures

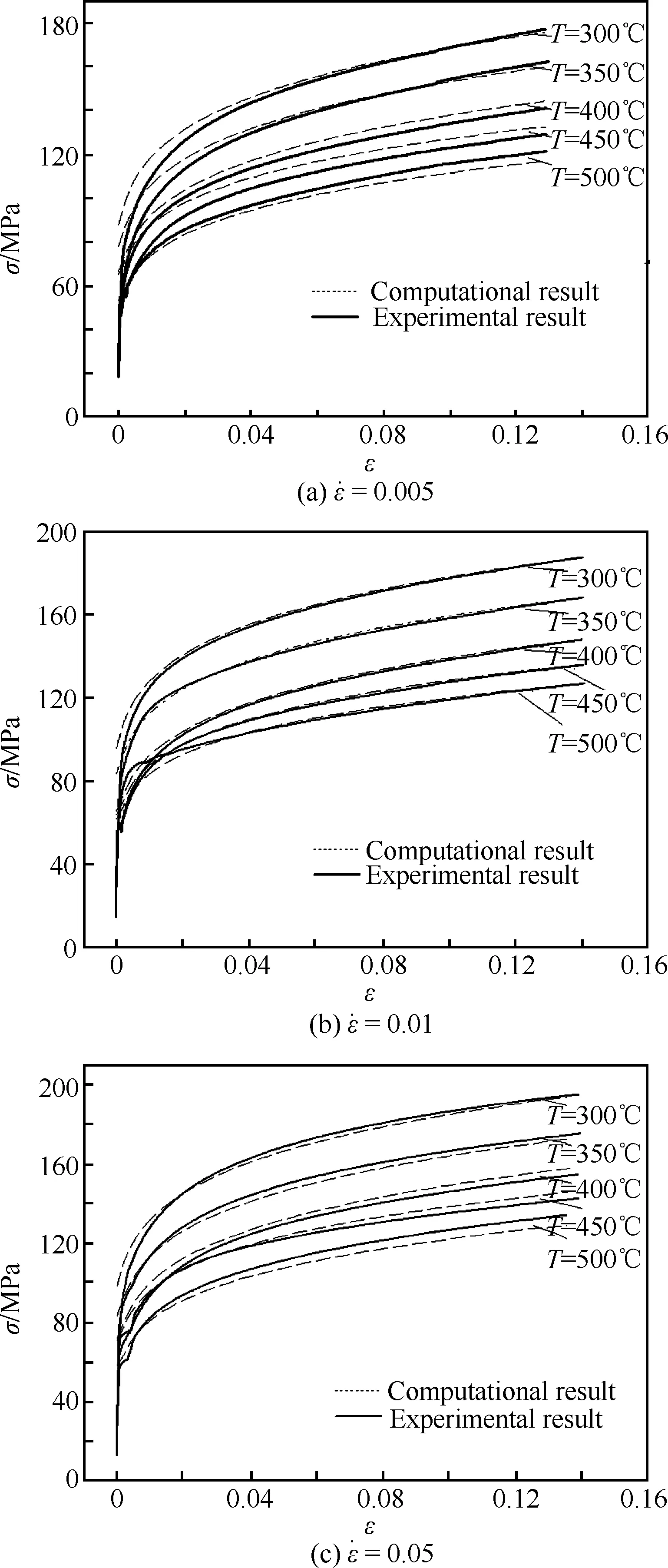
图10 管材真应力 －应变曲线Fig．10 Relationships between true stresses and strains

不同的响应面模型也对应着不同的全局最优解，进而能够反映出不同温度下剪应力本构参数的差别。在25、300、350、400、450和500 ℃温度范围内，获得了本构参数与距离函数的响应面模型，分别如式（15）～式（20）所示：

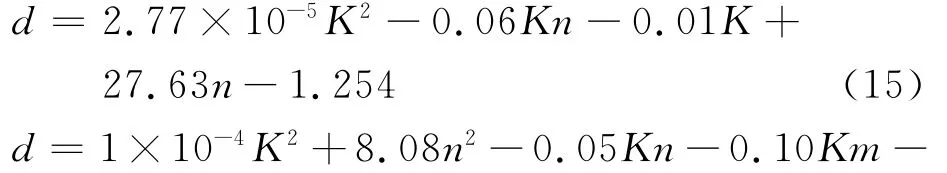
2．2．2 剪应力本构参数

基于式（15）～式（20），求最小距离函数，进而逆向识别出管材剪应力本构参数，如表3所示，可以发现，经过优化计算，min（d（T）：）＜0．04。

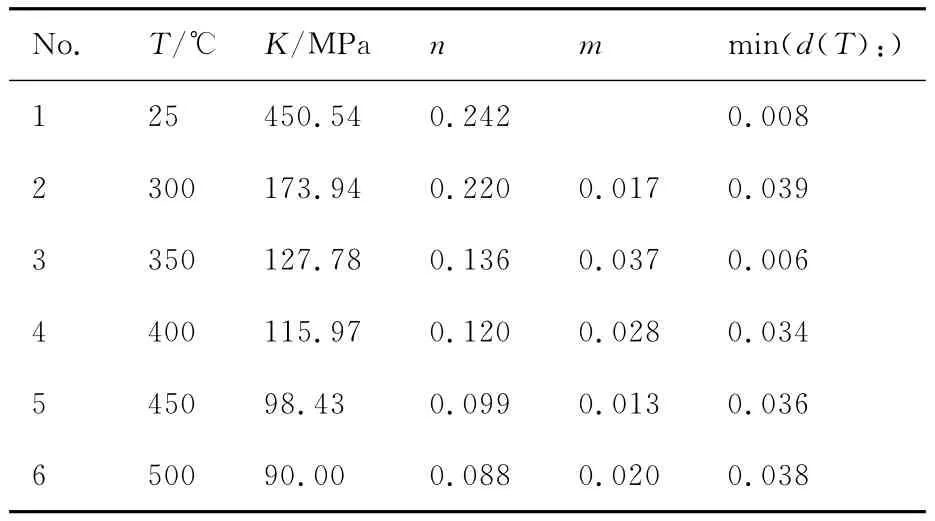
表3 剪应力本构参数Table 3 Constitutive parameters based on shear stress

图11为管材剪应力本构参数与温度倒数的关系，可以发现T越高，管材剪应力本构参数的K值和n值将减小，K值最大相对变化量为48%，n值最大相对变化量为59%；m值呈现波动的趋势，m值最大相对变化量为65%。当T∈［300，500］℃时，管材剪应力本构参数与温度的函数关系为

将逆向识别的管材剪应力本构方程用于模拟管材等温剪切测试过程，获得了剪切载荷与位移的曲线，并与实验曲线展开对比，结果如图12所示。可以发现，采用逆向识别本构参数模拟的力－位移曲线，与实验结果的最大相对误差为10%，因此，可以说，本研究提出的管材剪应力本构参数逆向识别方法是可靠的。

2．3 管材剪应力本构参数应用

分别采用单拉应力本构参数和剪应力本构参数模拟TA2钛管差温剪切弯曲过程，剪应力作用区域的管材厚向应变（εt）分布模拟结果与实验结果的对比，如图13所示。可以发现：①如

图11 剪应力本构参数与温度的关系Fig．11 Relationships between constitutive parameters based on shear stresses and temperatures

图13（a）所示，在测量区间1，单拉应力本构参数的模拟结果与实验结果的最大相对误差为23%，剪应力本构参数的模拟结果与实验结果的最大相对误差为9%，模拟精度提高了60%；②如图13（b）所示，在测量区间2，采用单拉应力本构参数的模拟结果与实验结果的最大相对误差为25%，剪应力本构参数的模拟结果与实验结果的最大相对误差变化不大，但是平均误差有所提高，相对误差由23%减小为15%，模拟精度提高了40%。

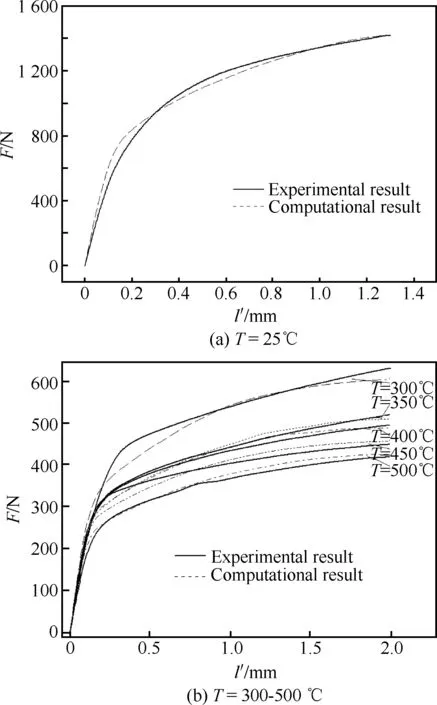
图12 模拟力－位移曲线与实验结果对比Fig．12 Comparison between simulation results of loaddisplacement curves and experimental ones

3 结 论

1）在修改的ASTM B831－05标准剪切管材试样基础上，提出了基于薄壁钛管剪切测试方法、剪切测试过程模拟有限元模型、以及基于距离函数的响应面模型相结合的管材剪应力本构参数逆向识别方法，能够可靠识别薄壁钛管剪应力本构参数。

2）当T∈［300，500］℃时，T 越高，TA2薄壁钛管剪应力本构参数的K值和n值将减小，K值最大相对变化量为48%，n值最大相对变化量为59%；m值呈现波动的趋势，m值最大相对变化量为65%。

3）与单拉应力本构参数相比，剪应力本构参数对温度的变化更敏感，且剪应力本构参数值较小。采用剪应力本构参数模拟TA2薄壁钛管差温剪切弯曲过程，管材最大剪应力区厚向应变分布的模拟精度较高，模拟精度最大提高了60%。

图13 模拟管材厚向应变分布与实验结果的对比Fig．13 Comparison between simulation results of tube thickness strain distributions and experimental ones

［1］ YANG H，LI H，ZHANG Z Y，et al．Advances and trends on tube bending forming technologies［J］．Chinese Journal of Aeronautics，2012，25（1）：1－12．

［2］ SONG F F，YANG H，LI H，et al．Springback prediction of thick－walled high－strength titanium tube bending［J］．Chinese Journal of Aeronautics，2013，26（5）：1336－1345．

［3］ JIANG Z Q，ZHAN M，YANG H，et al．Deformation behavior of medium strength TA18high－pressure tubes during NC bending with different bending radii［J］．Chinese Journal of Aeronautics，2011，24（5）：57－64．

［4］ TIAN S，LIU Y L，YANG H．Effects of geometrical parameters on wrinkling of thin－walled rectangular aluminum alloy wave－guide tubes in rotary－draw bending［J］．Chinese Journal of Aeronautics，2013，26（1）：242－248．

［5］ YAN J，YANG H，ZHAN M，et al．Forming characteristics of Al－alloy large－diameter thin－walled tubes in NC－bending under axial compressive loads［J］．Chinese Journal of Aeronautics，2010，23（4）：461－469．

［6］ ZENG Y S，LI Z Q．Experimental research on the tube push－bending process［J］．Journal of Materials Processing Technology，2002，122（2－3）：237－240．

［7］ ZHANG Z Y，YANG H，LI H，et al．Quasi－static tensile behavior and constitutive modeling of large diameter thinwalled commercial pure titanium tube［J］．Materials Science ＆Engineering A，2013，569：96－105．

［8］ TAO Z J，YANG H，LI H，et al．Quasi－static tensile behavior of large－diameter thin－walled Ti－6Al－4Vtubes at elevated temperature［J］．Chinese Journal of Aeronautics，2016，29（2）：542－553．

［9］ ZHAN M，HUANG T，YANG H．Variation of contractile strain ratio of Ti－3Al－2．5Vtubes and its effects in tubes numerical control bending process［J］．Journal of Materials Processing Technology，2015，217：165－183．

［10］ CARBONNIE｀RE J，THUILLIER S，SABOURIN F，et al．Comparison of the work hardening of metallic sheets in bending－unbending and simple shear［J］．International Journal of Mechanical Sciences，2009，51（2）：122－130．

［11］ AN Y G，VEGTER H，HEIJNE J．Development of simple shear test for the measurement of work hardening［J］．Journal of Materials Processing Technology，2009，209（9）：4248－4254．

［12］ CAO J，LEE W，CHENG H S，et al．Experimental and numerical investigation of combined isotropic－kinematic hardening behavior of sheet metals［J］．International Journal of Plasticity，2009，25（5）：942－972．

［13］ YIN Q，SOYARSLAN C，GUNER A，et al．A cyclic twin bridge shear test for the identification of kinematic hardening parameters［J］．International Journal of Mechanical Sciences，2012，59（1）：31－43．

［14］ YIN Q，ZILLMANN B，SUTTTNER S，et al．An experimental and numerical investigation of different shear test configurations for sheet metal characterization［J］．International Journal of Solids and Structures，2014，51（5）：1066－1074．

［15］ MERKLEIN M，BIASUTTI M．Forward and reverse simple shear test experiments for material modeling in forming simulations［C］／International Conference on Technology of Plasticity．Aachen：Steel Research International，2011：702－707．

［16］ G’SELL C，BONI S，SHRIVASTAVA S．Application of the plane simple shear test for determination of the plastic behaviour of solid polymers at large strains［J］．Journal Materials Science，1983，18（3）：903－918．

［17］ MIYAUCHI K．A proposal of a planar simple shear test in sheet metals［J］．Science Paper for Institute of Physical Chemistry Research，1984，78（3）：27－40．

［18］ ASTM International．ASTM B831－05Standard test method for shear testing of thin aluminum alloy products［S］．New York：ASTM，2005：1－4．

［19］ FRESNEL H，GROLLEAU V，LONGE’RE P，et al．Characterization of the shear behaviour of a thin－walled tubular material［J］．Thin－Walled Structures，2009，47（3）：295－303．

［20］ ASPENBERG D，LARSSON R，NILSSON L．An evaluation of the statistics of steel material model parameters［J］．Journal of Materials Processing Technology，2012，212（6）：1288－1297．

［21］ 孙志超，杨合，蔡旺，等．一种确定管材塑性本构关系的反算法［J］．重型机械，2000（3）：43－46．SUN Z C，YANG H，CAI W，et al．A reversion calculation method for determining the constitutive stress strain relationship of tubes［J］．Heavy Machinery，2000（3）：43－46（in Chinese）．

［22］ HARTH T，SCHWAN S，LEHN J，et al．Identification of material parameters for inelastic constitutive models：statistical analysis and design of experiments［J］．International Journal of Plasticity，2004，20（8－9）：1403－1440．

［23］ 闫晶，杨合，詹梅，等．一种确定管材本构参数的新方法及其应用［J］．材料科学与工艺，2009，17（3）：297－300．YAN J，YANG H，ZHAN M，et al．A new method to determine plastic constitutive parameters of tube and its applications［J］．Materials Science ＆ Technology，2009，17（3）：297－300（in Chinese）．

［24］ WEI D L，ZHEN Z S，CHEN J．Optimization and tolerance prediction of sheet metal forming process using response surface model［J］．Computational Materials Science，2009，42（2）：228－233．

［25］ WANG H，LI G Y，ZHONG Z H．Optimization of sheet metal forming processes by adaptive response surface based on intelligent sampling method［J］．Journal of Materials Processing Technology，2008，197（1－3）：77－88．

［26］ XUE X，LIAO J，VINCZE G，et al．Modelling of mandrel rotary draw bending for accurate twist springback prediction of an asymmetric thin－walled tube［J］．Journal of Materials Processing Technology，2015，216：405－417．

［27］ 理有亲，林兆荣．钛板冲压成形技术［M］．北京：国防工业出版社，1986：185－186．LI Y Q，LIN Z R．Ti－alloy sheet metal forming technology［M］．Beijing：Defense Industry Press，1986：185－186（in Chinese）．

［28］ 《中国航空材料手册》编辑委员会．中国航空材料手册［M］．北京：中国标准出版社，2001：10－20．Editor Commitee of China Aeronautical Materials Handbook．China aeronautical materials handbook［M］．Beijing：China Standard Press，2001：10－20（in Chinese）．

［29］ 任露泉．回归设计及其优化［M］．北京：科学出版社，2009：39－46．REN L Q．Regression design and its optimization［M］．Beijing：Science Press，2009：39－46（in Chinese）．

［30］ Hibbit Karlson and Sorensen Inc．．Abaqus 6．9documentation［M］．Washington，D．C．：Hibbit Karlson and So－rensen Inc．，2009：180－200．

［31］ 赵镇南．传热学［M］．北京：高等教育出版社，2002：493－508．ZHAO Z N．Heat transfer［M］．Beijing：Higher Education Press，2002：493－508（in Chinese）．

［32］ 马高山，万敏，吴向东．5A90铝锂合金热态下本构关系研究［J］．塑性工程学报，2007，14（3）：68－71．MA G S，WAN M，WU X D．Research on the constitutive relationship of 5A90aluminum—lithium alloy at hot forming temperature［J］．Journal of plasticity engineering，2007，14（3）：68－71（in Chinese）．

Identification method of shear stress constitutive parameters of Ti－alloy thin－walled tube

YAN Jing1，2，3，＊ ，WU Wei1，2，3
1．Aeronautical Key Laboratory for Plastic Forming Technology，Beijing 100024，China 2．Beijing Key Laboratory of Digital Plastic Forming Technology and Equipment，Beijing 100024，China 3．Beijing Aeronautical Manufacturing Technology Research Institute，Beijing 100024，China

The identification of shear stress constitutive parameters（SSCPs）of Ti－alloy thin－walled tubes（TATTs）at different temperature levels（DTLs）is a key problem for the research of plastic deformation behavior in these tube shear bending processes under differential temperature fields constraints（DTFCs）．A tube shear test method is presented．The TATTs isothermal shear test processes under the DTLs，the finite element（FE）models for simulating these test processes and the response surface models based on distance functions have been combined to present a reverse method for identifying these SSCPs of the TATTs under the DTLs．Then，this method is used for identifying the SSCPs of TA2TATTs．A 3Dcoupled thermalmechanical elastic－plastic FE model for simulating these shear bending processes under DTFCs of the TA2TATTs is established．An experimental bending process is simulated by this FE model using the SSCPs and the uniaixal tension stress constitutive parameters（UTSCPs）respectively，and the reliability of this FE model is estimated．The results reveal that for SSCPs，the larger the temperature，the smaller the values of Kand n；the value of mfluctuates；the effects of temperature on the SSCPs are larger than the UTSCPs and the values of the SSCPs are smaller．The computational precision level of the FE model using the SSCPs is larger than the UTSCPs by 60%．

Ti－alloy thin－walled tube；constitutive parameter；shear stress；parameter identification；finite element

2015－09－28；Revised：2015－10－20；Accepted：2015－10－27；Published online：2015－11－26 13：51

URL：www．cnki．net／kcms／detail／11．1929．V．20151126．1351．012．html

National Natural Science Foundation of China（51305415）

V261．3

A

1000－6893（2016）09－2884－11

10．7527／S1000－6893．2015．0289

2015－09－28；退修日期：2015－10－20；录用日期：2015－10－27；网络出版时间：2015－11－26 13：51

www．cnki．net／kcms／detail／11．1929．V．20151126．1351．012．html

国家自然科学基金 （51305415）

＊通讯作者．Tel．：010－85701254 E－mail：yanjing2008win＠163．com

闫晶，吴为．薄壁钛管剪应力本构参数识别方法［J］．航空学报，2016，37（9）：28842－894．YAN J，WUW ．Identification method of shear stress constitutive parameters of Tia－lloy thin－walled tube［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：28842－894．

闫晶 男，博士，高级工程师。主要研究方向：航空钣金成形过程建模与仿真。

Tel．：010－85701254

E－mail：yanjing2008win＠163．com

＊Corresponding author．Tel．：010－85701254 E－mail：yanjing2008win＠163．com