超磁致伸缩电静液作动器的试验研究与特性分析

杨旭磊，朱玉川＊，纪良，费尚书，郭亚子

南京航空航天大学机电学院，南京 210016

超磁致伸缩电静液作动器的试验研究与特性分析

杨旭磊，朱玉川＊，纪良，费尚书，郭亚子

南京航空航天大学机电学院，南京 210016

超磁致伸缩材料驱动的电静液作动器具有结构高度集成、性能影响因素多以及理论分析复杂等特点，为寻求超磁致伸缩电静液作动器可靠的理论分析方法以提高其输出性能，首先搭建了超磁致伸缩执行器与作动器试验测试平台，完成了执行器与作动器动态特性对比试验，在准确测试与观察试验现象的基础上，对超磁致伸缩电静液作动器进行结构分解，以各环节固有频率为理论分析切入点，采用试验、理论与有限元分析相结合的方法，分析了悬臂梁阀片、管路、液压缸以及蓄能器等动态特性对作动器输出性能的影响规律，总结出符合试验结果的理论分析方法并确定了影响与制约作动器输出性能的关键环节，最后提出了超磁致伸缩电静液作动器优化改进方案，优化后作动器试验结果显示：在200Hz左右、0．6MPa的偏压作用下，选取0．15mm 厚度的阀片，作动器的输出性能达到最佳，其输出流量最大可达1．2L／min。

超磁致伸缩材料；电静液作动器；动态特性；试验研究；输出性能；优化

相比于液压系统管路和附件遍布全机的传统机载液压系统，电静液作动器是一种集成化、模块化的新型机载作动器［1－2］。随着现代飞机特别是军用飞机正朝着高速、高机动性、高战斗力与高能效方向发展，研制高性能的新型电静液作动器具有重要的现实意义［2－3］。智能材料是一种新兴的功能性材料，其优良的特性使研制以智能材料为驱动元件的电静液作动器成为了可能，并可通过实现阀泵缸高度集成化来消除油箱与管路，以此提高作动器的可靠性［4－6］。目前，国外已经将压电－液压作动器应用到了智能旋翼机中，但是研究发现在高频工作中，压电材料由于磁滞损耗而产生的大量热会影响其工作并有可能永久破坏压电材料［7－8］。

超磁致伸缩材料（Giant Magnetostrictive Material，GMM）作为智能材料的一种，不仅具有输出力大、能量密度高、响应速度快、抗干扰能力强等优点［9－11］，而且相比于压电材料具有更小的磁滞损耗以及更好的高温特性，为研制新型高性能的超磁致伸缩电静液作动器（GMM－based Electro－Hydrostatic Actuator，GMEHA）提供了有效的途径［12－13］。

目前，国外已经对GMEHA的特性进行了大量的研究：美国马里兰大学的Chaudhuri等［8］在总结前人经验的基础上，综合考虑阀片的动态特性、油液的惯性以及可压缩性等因素建立了较为准确的数学模型，通过对模型进行仿真，分析了阀片的动态特性对GMEHA输出性能的影响，但未对其进行相关试验验证，并猜测作动器的输出流量随驱动频率的增加出现两个峰值，分别是由系统中油液共振以及GMM棒、活塞等零件的机械共振造成的；美国宾夕法尼亚大学的Kim和Wang［14］也发现了类似的试验现象，并认为双作用输出缸低压侧的腔体就相当于一个亥姆霍兹共振器，该结构会影响到吸入流量，并最终造成输出流量在某些特定的频率范围的突然下降，从而使作动器的输出流量出现两个峰值；美国俄亥俄州立大学的Larson和Dapino［15］基于J－A磁化模型在AMEsim中建立GMEHA的仿真模型，并对仿真结果与试验结果进行了对比，但未对试验现象进行详细的说明。

此外，Lindler等［16］提出了一个压电液压作动器的输出功率模型，Cadou和Zhang［17］提出了一个150Hz以下的低频与准静态模型，Nasser等［18］提出了一个线性与集中参数数学模型，可预测液压缸的单向运动，Oates和Lynch［19］提出了一个系统动态模型，可预测电－磁－流体的多场耦合行为。但这些模型的研究重点集中于系统最终的输出，并未对系统各环节的动态特性予以专门研究，故未能揭示系统各个环节对系统最终性能的影响。

本文在上述研究的基础上，以试验现象作为研究的发起点，以最大化GMEHA的输出性能为目的，通过对GMEHA各部件进行动态特性理论分析，得出了作动器的输出流量随驱动频率的增加出现两个峰值这一现象的原因，并对此进行了试验验证；然后进一步测试了不同条件下GMEHA的输出性能，总结出了影响其输出性能的限制因素，并提出了解决方案，为高性能GMEHA的研制奠定了基础。

1 GMEHA的结构与工作原理

图1（a）为设计的GMEHA，其主要包括5个部分：超磁致伸缩执行器（Giant Magnetostrictive Actuator，GMA）、泵体、液压缸、蓄能器以及管路与配件［11，20］，如图1（b）所示。其中 GMA 作为GMEHA的动力核心，其工作过程主要通过驱动线圈产生交变磁场，磁力线经GMM棒、底座、外壳、导磁块以及输出杆形成闭合回路［7］，最终将GMM棒磁化并产生位移推动活塞不断往返运动压缩油液，被压缩的油液经过单向阀的整合配流为GMEHA提供输出动力。

图1 GMEHA结构及原理图Fig．1 Structure and schematic diagram of GMEHA

如图2所示，GMEHA的工作原理分为以下4个阶段［21－22］：①压缩，在这个阶段，泵腔内的压

强小于泵腔外的压强，两个阀片都是关闭的，随着GMM棒的伸长，腔内的流体被压缩。②排油，这时腔内外压差大于零，排油阀被打开，腔内的油液经管路流入液压缸高压侧，推动负载运动。③回扩，该阶段通电线圈的电流开始减少，驱动磁场也随之减弱，导致GMM棒开始回缩，由于蓄能器与腔内的压差小于零，所以吸油阀紧闭，无油液进入腔内。④吸油，随着GMM棒的回缩，腔内的压强迅速降低，当腔内外的压力差足以打开吸油阀片，油液进入腔内。

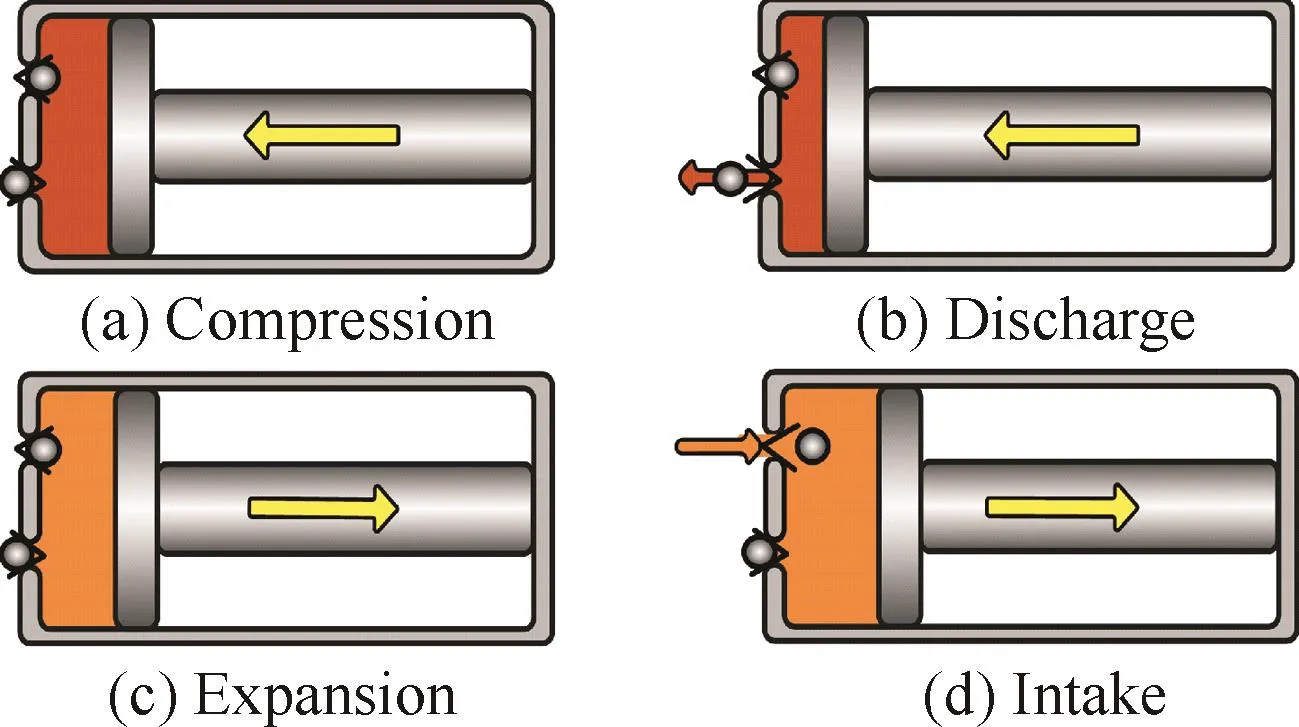
图2 GMEHA工作原理Fig．2 Operational principle of GMEHA

2 试验平台搭建与测试

为得到有效的试验数据进行比较，分别搭建GMA与GMEHA输出性能测试试验平台。

2．1 GMA

图3为GMA测试试验台，图3中信号发生器和恒流功率放大器提供频率与幅值均可调节的驱动电流，激光位移传感器（CD5－30（A），精度为0．2μm，量程为1cm，采样频率为10kHz）测试GMA的输出位移。

图3 GMA测试试验台Fig．3 Bench of GMA test

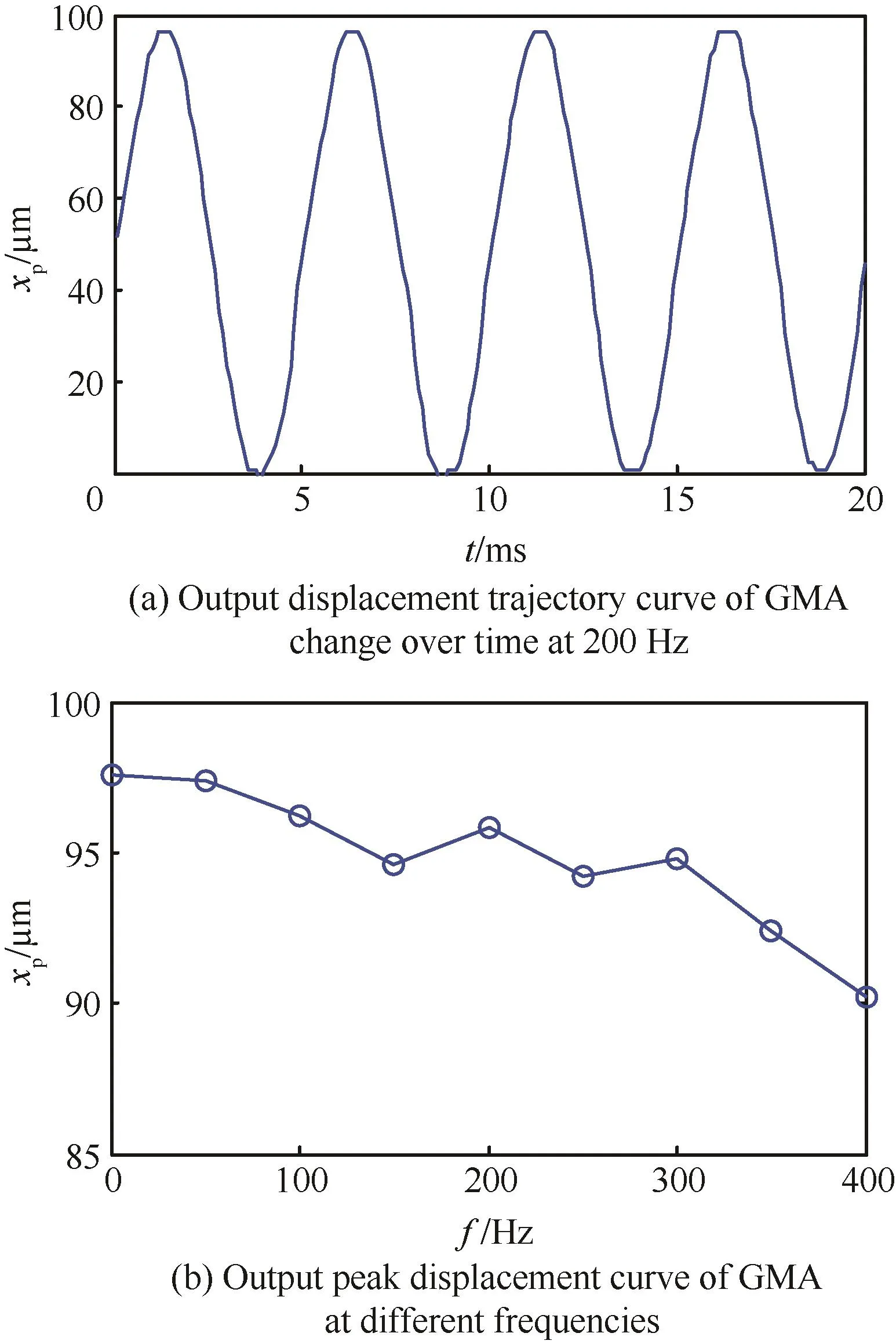
图4 GMA输出位移特性Fig．4 Output displacement characteristics of GMA

在幅值为3A的正弦交变电流和3A的偏置电流作用下，GMA的输出位移特性如图4所示，xp为GMA的输出位移，t为时间，其中，图4（a）为GMA在工作频率为200Hz时的输出位移轨迹随时间的变化曲线，图4（b）为不同工作频率时GMA的输出峰值位移曲线。图4（b）中横坐标f为正弦电流驱动频率。由图4可以看出，GMA展示出较好的输出性能，其最大输出峰值位移接近98μm，且400Hz时也能达到90μm，这使GMEHA的驱动部分得到了保证。

2．2 GMEHA

图5为根据GMEHA的工作原理搭建的GMEHA测试试验台。在幅值为3A的正弦交变电流和3A偏置电流的作用下，对不同工作频率下的GMEHA输出性能进行测试。通过激光位移传感器（CD－33，精度为2．5μm，量程为12cm，采样频率为1kHz）测量液压缸输出杆的位移，并结合采样时间以及液压缸的横截面积反推出GMEHA的输出流量。在0．6MPa的偏压作用下，不同驱动频率时GMEHA输出流量曲线如图6所示。图6中纵坐标为GMEHA的输出流量Q，从图6中可以看出，GMEHA在300Hz左右输出流量最大而在150Hz左右最低，与图4中GMA的输出位移特性并不一致。因此，系统中部分环节的动态响应限制了GMEHA的输出性能，而由图4可以排除包括驱动电流在内的GMA之前的环节的影响。GMA之后的环节如悬臂梁阀片、管路中油液、液压缸以及蓄能器的动态性能都有可能对GMEHA的输出性能产生影响。

图5 GMEHA测试试验台Fig．5 Bench of GMEHA test

图6 GMEHA输出流量曲线Fig．6 Output flow rate curve of GMEHA

3 GMEHA的动态特性分析

采用有限元与理论分析相结合的方法对悬臂梁阀片、管路中的油液、液压缸以及蓄能器动态特性进行分析。

3．1 悬臂梁阀片

流体流入阀体中将阀片打开而流岀的过程是一个流体与阀片相互影响的复杂的流固耦合过程。因此，阀片在流体中的动态特性通过理论计算很难得到用初等函数表示的解。为提高结果的正确性且便于分析，本文基于流固耦合力学方法，利用COMSOL Multiphysics有限元软件建立了悬臂梁阀体流道模型，仿真参数如表1所示。通过在阀体入口与出口处给定压差进行流固耦合数值模拟，并对其动态特性进行分析。

悬臂梁阀片的有限元分析如图7所示，其中，图7（a）为阀片的有限元模型，图7（b）为阀片的流固耦合仿真结果，vR为阀中流体的流速。阀片受到压差作用会发生变形而使流体通过，这个过程虽然是一个复杂的非线性过程，但由于阀片变形量较小，为简化分析，可以将阀片的变形进行线性化处理，将阀片在流体中的变形简化为一个单自由度的弹簧阻尼器［22］。

图8为阀片的等效动力学模型，图中：pch为泵腔内的压强；pt为管路入口处的压强；xR为阀片等效开口位移；mR为阀片的等效质量；kR为阀片的等效刚度；cR为阀片在油液中运动的阻尼。由图8可知，当pch＞pt时，阀片两侧就会出现压差ΔpR，当压差ΔpR达到一定值时，阀片会在压差的作用下打开，利用阀片打开这个响应过程可以对阀片进行动态特性分析。图9为不同压差时阀片的动态响应特性。

表1 仿真参数Table 1 Simulation parameters

图7 阀片的有限元分析Fig．7 Finite element analysis of reed valve

图8 阀片的等效动力学模型Fig．8 Equivalent dynamic model of reed valve

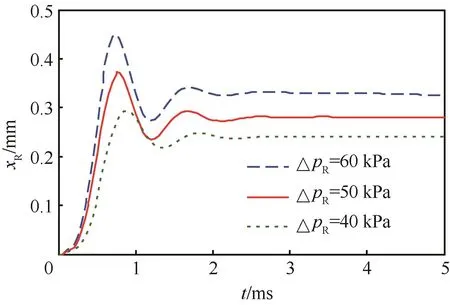
图9 不同压差时阀片的动态响应Fig．9 Dynamic response of reed valve under different pressure differential

利用图9中阀片的响应曲线可以计算得到阀片响应的峰值时间tP以及最大超调量σ。对于单自由度弹簧阻尼器，其动态传递函数可以表示为

式中：ωR为阀片谐振角频率；ξR为阻尼比。

联立式（2）和式（3）可以求出阀片在不同压差时的谐振角频率ωR和阻尼比ξR，如表2所示。根据表2中的数据，计算取平均值可得阀片固有频率约为700Hz左右。

表2 不同压差时阀片的响应参数Table 2 Response parameters of reed valve under different pressure differential

3．2 管 路

分析油液在管路中的非恒定流动时，可把长管路分成无数个单元，每个单元均由液阻、液容、液感组成，取出其中长度为Δx的一段，管路内压强和流量在Δt时间内的变化分别为［23］

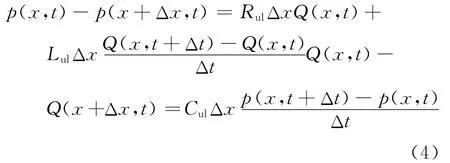
式中：p为管道内流体压强；Q为管道内流体流量；Rul、Lul和Cul分别为单位长度管路的液阻、液感和液容；x为油液在管路中的位置。

当Δt→0和Δx→0时，由式（4）可以得到的微分方程并对其进行拉普拉斯变换，初始值为零，可得

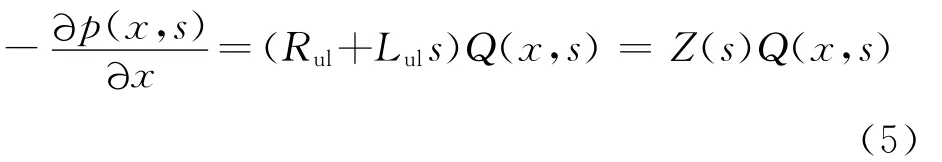
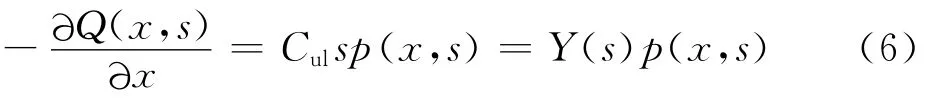
式中：Z（s）＝Rul＋Luls；Y（s）＝Culs。

将式（5）对x求偏导并将式（6）代入得

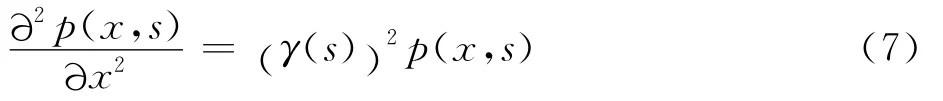
对式（7）求通解可得

式中：A1、A2为任意常数。

令

式中：Γ（s）为传播算子，Γ（s）＝γ（s）l，l为管路的长度。

在特性阻抗为Z0（s）的液压管路系统，负载阻抗为ZR（s）＝p2（s）／Q2（s），则可得输入端的液源阻抗为

对式（11）进一步整理得

在频率较高的情况下，层流单位液阻与单位液容和单位液感比起来很小，可以忽略不计，以s＝j w 代入式（12）中，因为ch（jlω／c）＝cos（l·ω／c），sh（jlω／c）＝jsin（lω／c），则

对于开端管路，其负载阻抗ZR（jω）为零，对式（13）化简可得液源阻抗为

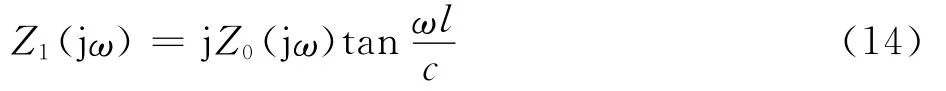
ωl／c＝nπ时，Z1（jω）＝0，管路发生谐振，由此可以求出此种情况下管路的最低固有频率为5 650Hz（管路长度l＝60mm）。

对于闭端管路，其负载阻抗ZR（jω）为∞，将式（13）分子分母都除以ZR（jω）可得液源阻抗为时，Z1（jω）＝0，管路发生谐振，

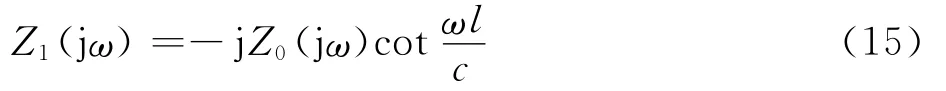
由此可以求出此情况下管路的最低固有频率为2 825Hz。

综上所述，接有液压缸的GMEHA管路属于接有变容积容腔的管路，其最低固有频率应介于在2 825～5 650Hz之间。

3．3 液压缸

液压缸作为GMEHA的执行机构，其动态性能的优劣将直接关系到GMEHA的输出性能，图10为液压缸工作原理图。图10中：Q1为流入高压腔的流量；Q2为流出低压腔的流量；V1为高压腔的容积；V2为低压腔的容积；p1为高压腔的压强；p2为低压腔的压强；Ap为活塞的有效作用面积；Mt为活塞与负载的总质量。

图10 液压缸工作原理图Fig．10 Operational principle diagram of hydraulic cylinder

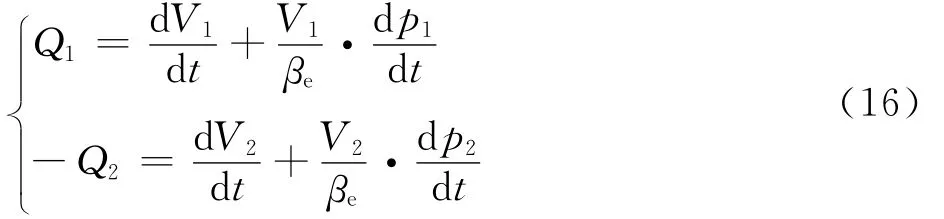
对两活塞腔应用连续性方程，可得［24］

液压缸两腔的体积为

式中：xp为活塞的位移；V01和V02分别为高压腔和低压腔的初始容积。

为简化分析，假定活塞处在中间位置，两个初始容积是相等的，即

液压缸总容积为

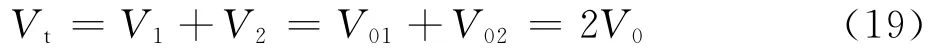
这个容积是一个常数，与活塞的位置无关。

在初始容积相等的条件下，由式（16）可得流量的连续性方程

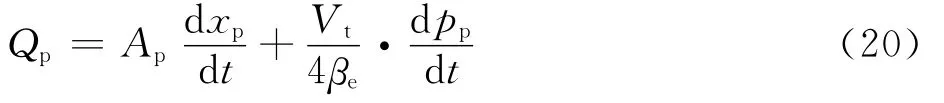
式中：Qp为液压缸的流量；pp为液压缸两腔的压差。

活塞动态力平衡方程的拉氏变化式为

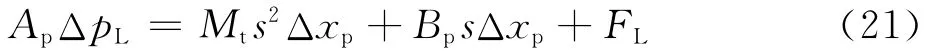
式中：Bp为液压缸的总黏度系数；FL为作用在活塞上的外力。

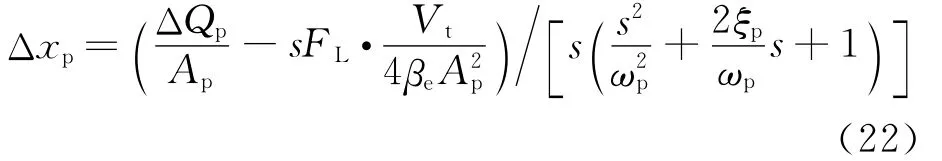
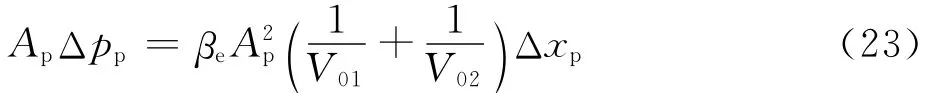
式中：ωp为活塞在中间位置时的谐振角频率；ξp为液压缸的阻尼比。

由此得液压缸的两腔的总液压弹簧刚度为

可见，当V01＝V02时，即当活塞处于中间位置时，K最低，稳定性最差，从而给出了最低的固有频率为1 286Hz。

3．4 蓄能器

蓄能器主要给系统提供偏压以提高油液的刚度，维持低压侧的压强和减少压力脉动，其工作原理图如图11所示。图11中：pe为蓄能器入口处的压强；pbias为蓄能器内提供的系统偏压（即充油后蓄能器内气体压强）；Va为蓄能器内气体的体积；la为蓄能器内的油液的高度；Aa为蓄能器的横截面积；Qa为蓄能器的瞬时流量。

图11 蓄能器工作原理图Fig．11 Operational principle diagram of accumulator

根据图11所示的蓄能器的工作原理得到蓄能器内的油柱运动微分方程为

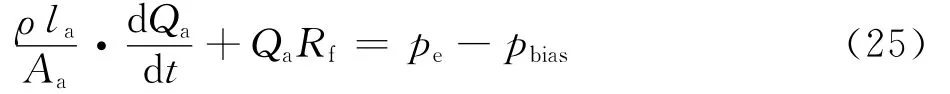
式中：Rf为油液的液阻，可以表示为

式中：μ为油液的动力黏度；da为蓄能器的内径。蓄能器的流量平衡方程为

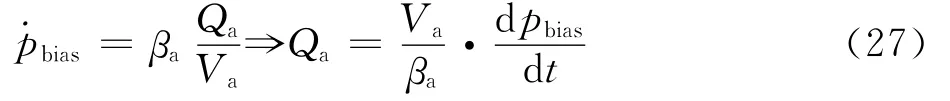
式中：βa为气体的体积弹性模量。将式（

一定量的理想气体在等温条件下，由波意耳定理可知：

式中：k为等熵指数，对于氮气k＝1．4。对式（30）求导可得

由式（31）可得气体的体积弹性模量的表达式为

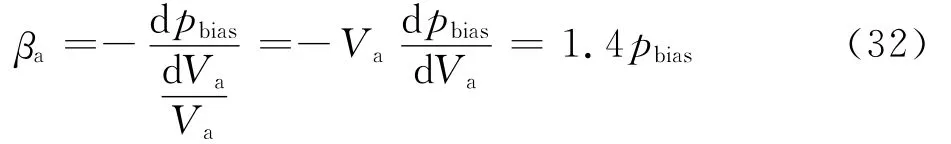
由式（28）可得蓄能器的谐振角频率为

将式（32）代入式（29）可得

蓄能器参数如表3所示，根据表3中数据可以求出蓄能器内气体的体积以及蓄能器内油液的高度，结合已知参数，根据式（33）可以求得蓄能器固有频率为139．5Hz。

表3 蓄能器参数Table 3 Accumulator parameters

4 GMEHA输出性能试验研究

4．1 蓄能器的影响

通过以上分析可以发现，蓄能器的共振频率刚好发生在150Hz左右，为确定图6中谷值输出流量频率与蓄能器固有频率的相关性，进一步进行蓄能器频域分析，结果如图12所示。

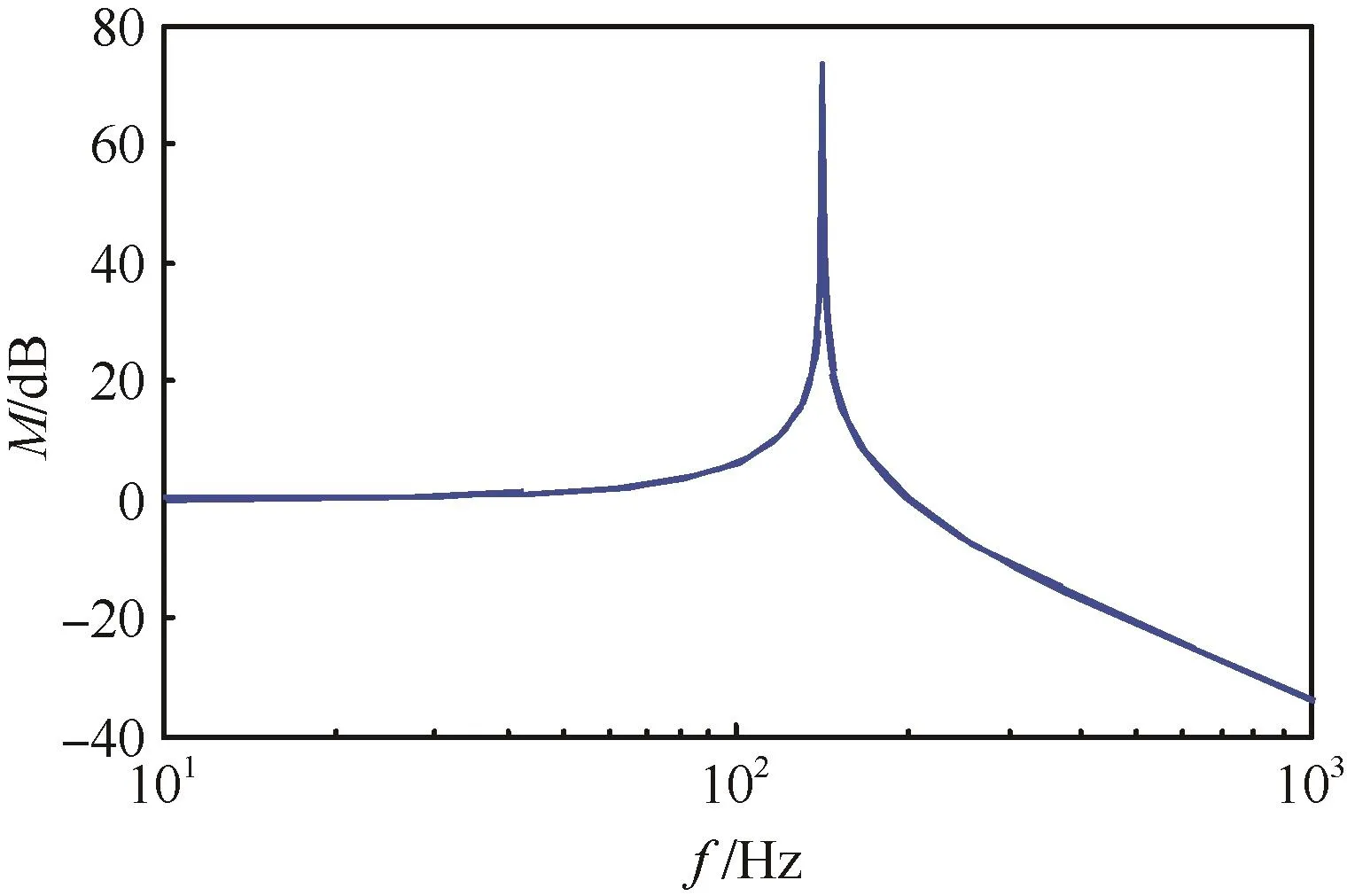
图12 蓄能器动态性能频域分析Fig．12 Dynamic performance analysis of accumulator at frequency domain

图12中：横坐标为系统的振动频率；纵坐标为蓄能器输出流量的对数幅值比。从图12中可以看出，蓄能器在100Hz时振动幅值开始增大，并且到150Hz左右达到振动峰值，这将导致蓄能器吸排油能力大大增加，又由于管路中油液黏性阻力的影响会造成蓄能器响应出现一定的滞后，导致在泵腔吸油过程中，大量的油液储存在蓄能器中不能及时排出使泵腔的吸油量减少，在泵腔排油过程中，蓄能器中油液排出到液压缸的低压侧阻碍液压缸运动，从而抑制GMEHA的输出性能。超过150Hz后，蓄能器的振幅将会开始衰减，其对泵腔吸排油的影响逐渐减弱，GMEHA的输出性能开始提高，而此时蓄能器在系统的作用主要是提供偏压以及提高油液刚度。

为通过试验来验证蓄能器动态特性的影响，分别在球阀打开与关闭的情况下（球阀打开蓄能器接通，球阀关上蓄能器不接通），测试不同驱动频率时GMEHA的输出流量变化情况，如图13所示。

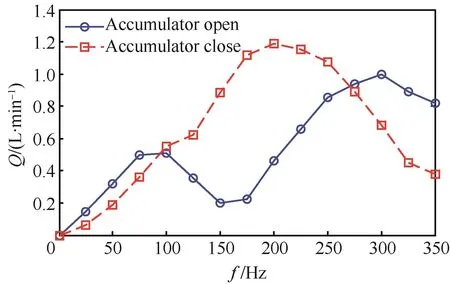
图13 球阀打开与关闭时GMEHA的输出流量Fig．13 Output flow rate of GMEHA when accumulator open and close

由图13可知，蓄能器的动态特性是影响GMEHA充分发挥性能的关键，当不使用蓄能器时，在一定的频率段可以有效的提高GMEHA的输出性能。然而在100Hz以下以及300Hz以上时，可以发现接有蓄能器的GMEHA输出性能明显好于没有接蓄能器的性能。这主要是因为在没有接蓄能器的情况下，液压缸输出位移时将会压缩低压侧的油液，使低压侧的压强会迅速上升从而阻碍液压缸活塞的运动；而当接有蓄能器时，由于气体的刚度远小于油液的刚度，被压缩的油液通过压缩蓄能器气囊中的气体而使低压侧的压力变化不大，从而减少了对液压缸活塞运动的阻碍。除此之外，蓄能器还能够有效地为系统补充由于泄漏等原因损失的油液。因此，为最大化GMEHA输出性能，蓄能器的存在是必要的。提升蓄能器的动态性能是提高GMEHA输出性能的一个重要因素。由式（33）可以看出，要提高蓄能器的动态性能，要适当提高蓄能器的刚度以及尽量选择容积小且横截面积较小的蓄能器。

4．2 系统偏压的影响

为提高GMEHA输出性能，油液的有效体积弹性模量也至关重要，其值主要取决于油液中混入空气的多少以及所施加偏压的大小，而完全排净油液中的空气几乎是不可能的，因此主要通过提高系统偏压来提高油液有效体积弹性模量，图14为不同偏压时，GMEHA的输出流量随驱动频率变化的曲线。

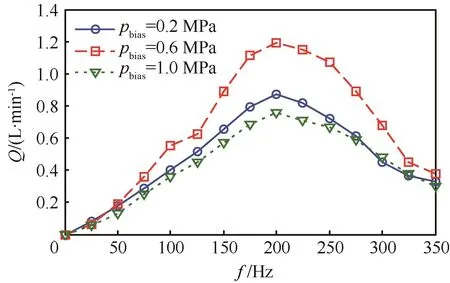
图14 不同偏压时GMEHA输出流量实测曲线Fig．14 Measured curves of GMEHA output flow rate under different bias pressures

从图14中可以看出，系统偏压太大或太小都不利于作动器充分发挥性能。偏压太小时，油液有效体积弹性模量也会相应的减小，GMM输出位移有一部分会消耗在压缩油液上，而且在泵腔吸油过程中，过小的偏压会导致泵腔内外的压差太小而不能使足够的油液进入泵腔，影响GMEHA输出性能。而当偏压过大时，虽然油液体积弹性模量提高，但泵腔内压力也随之增大，GMM棒输出位移时需要克服更大的压力，这将会减小GMM棒输出位移，从而影响GMEHA输出性能。综上所述，偏压需要根据实际情况选择合适值使GMEHA输出性能最优。

4．3 悬臂梁阀片的影响

观察图13可以看出，在排除蓄能器影响的情况下，在200Hz以后，GMEHA的输出性能开始下降，而且在超过250Hz以后下降尤为明显。主要因为随着频率的升高，惯性负载的作用越来越明显，GMM棒的输出峰值位移不断减小；除此之外，阀片的响应也是一个不可忽略的因素，因为随着驱动频率的提高，阀片的响应速度相对于驱动频率没有达到足够快，这势必将会造成阀片响应出现一定量的滞后，在GMEHA工作过程中，由于阀片的滞后必然会造成一定量的回流（流出泵腔的油液，由于阀片不能及时关闭导致油液又流回泵腔的现象），这将会造成GMEHA输出性能的下降。图15为通过有限元软件模拟的阀片开口位移随驱动压力变化的曲线。

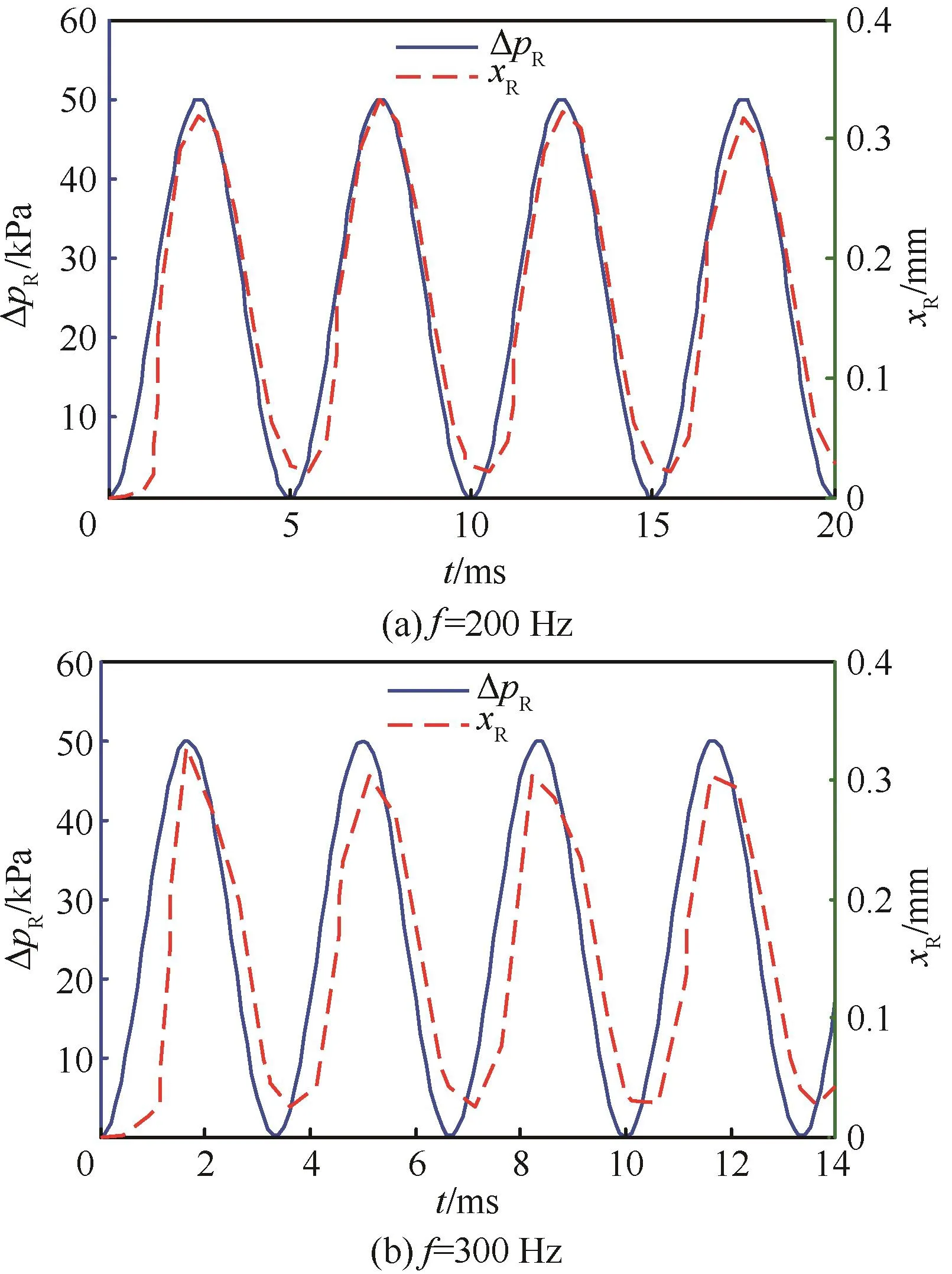
图15 阀片开口位移随驱动压力变化的曲线Fig．15 Curves of opening displacement of reed valve changed with driving pressure

从图15中可以看出，在200Hz时，阀片的动态响应能够很好的跟随压力的变化，这表示在200Hz的时候，阀片的响应足够迅速，能够及时关闭防止回流现象的发生；而在300Hz的时候，阀片的响应就出现了较为明显的相位滞后，这势必导致阀片不能及时关闭而造成一定量的回流，从而影响GMEHA输出性能。

为揭示阀片动态性能对作动器的影响，通过激光位移传感器测量了液压缸的输出位移轨迹，图16为工作频率为200Hz和300Hz时，GMEHA输出位移随时间变化曲线。

图16中纵坐标为液压缸输出位移。虽然由于激光位移传感器采样频率（采样频率为1kHz）的限制，图16中不能够完全反映液压缸的输出位移轨迹，但是从采到的数据点得到轨迹曲线已经足够反映回流现象是否存在。如图16（a）所示，在200 Hz的时候，液压缸的输出位移轨迹呈现上升跟停滞保持不断交替，这是由于GMM棒周期性的伸长和缩短。在GMM棒伸长时，通过压缩油液推动液压缸上升；而在GMM棒缩短过程中，排油阀片及时关闭而使高压侧的油液不能回到泵腔，这样能使泵腔吸油时，液压缸的位置保持不变。这反映了在200Hz时，阀片响应速度相对于驱动频率足够快，没有出现回流现象。如图16（b）所示，液压缸的输出位移轨迹存在下降现象，这正是由于阀片响应速度相对于驱动频率不是足够快，导致阀片不能够及时关闭，从而在泵腔吸油过程中，高压侧的油液又回流到泵腔导致液压缸输出位移下降。图16展示的试验结果与仿真结果有着很好的一致性，也从侧面反映了有限元仿真软件的可预测性。

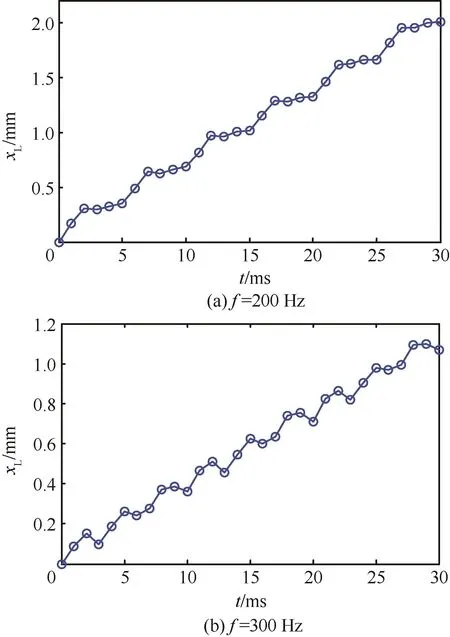
图16 GMEHA输出位移实测曲线Fig．16 Measured curves of output displacement of GMEHA

为避免回流现象的出现就必须提高阀片的响应速度，通过提高阀片的刚度来提高阀片的响应速度或许是一种简单有效的方法，图17为选用不同厚度的阀片时，GMEHA输出流量随驱动频率变化的曲线。

图17 选择不同厚度阀片时GMEHA输出流量实测曲线Fig．17 Measured curves of GMEHA output flow rate of reed valves with different thicknesses

从图17中可以看出，对比0．15mm的阀片，0．20mm厚度的阀片使GMEHA输出性能在200Hz以后的衰减速度明显减缓，主要由于刚度的提高而使响应频率提高进而减少回流量。而使用0．20mm阀片时，GMEHA的整体输出性能却不如使用0．15mm厚度的阀片，这是因为阀片刚度的提高，打开阀片所需要的压差也相应的提高，更多的压强用于打开阀片而使输出的压强有所减少。因此，高频响低阻力的单向阀对于充分发挥GMEHA的输出性能起着至关重要的作用。

5 结 论

1）通过试验测试GMA的输出性能，在3A的交变电流以及3A的直流偏置的作用下，GMA具有较好的输出性能，其最大输出峰值位移能够达到接近98μm，而且在400Hz也能够达到90μm。

2）通过有限元与理论计算相结合的方法，分析了阀片、管路油液、液压缸以及蓄能器的动态响应特性，其固有频率分别为700、2 825～5 650、1 286和139．5Hz。

3）经过理论分析并通过试验验证了蓄能器的动态响应特性是限制GMEHA输出性能的主要因素；通过试验分析了蓄能器在系统中的重要作用，而且其提供偏压的大小都对GMEHA输出性能有着较大的影响。

4）经过有限元数值模拟分析并通过试验验证了阀片的动态特性对GMEHA输出性能的影响，阀片的刚度过低会导致阀片响应速度慢以至于在高频驱动的条件下出现回流；而阀片刚度过大又会造成压力损失增大，影响GMEHA的输出性能。

5）通过测试，200Hz的工作频率以及0．6MPa偏压作用下，GMEHA在选择0．15mm厚度的阀片时，其输出性能达到最佳，最大输出流量达到1．2L／min。

［1］ GOHARDANI A S，DOULGERIS G，SINGH R．Challenges of future aircraft propulsion：a review of distributed propulsion technology and its potential application for the all electric commercial aircraft［J］．Progress in Aerospace Sciences，2011，47（5）：369－391．

［2］ 王占林，陈斌．未来飞机液压系统的特点［J］．中国工程科学，1999，1（3）：5－10．WANG Z L，CHEN B．Characters of future aircraft hydraulic system［J］．Engineering Science，1999，1（3）：5－10（in Chinese）．

［3］ SANDERS B，CROWE R，GARCIA E．Defense advanced research projects agency－smart materials and structures demonstration program overview［J］．Journal of Intelligent Material Systems and Structures，2004，15（4）：227－233．

［4］ WAX S G，FISCHER G M，SANDS R R．The past，present，and future of DARPA’s investment strategy in smart materials［J］．Journal of the Minerals，Metals and Materials Society，2003，55（12）：17－23．

［5］ SNEED R C，SMITH R R，CASH M F，et al．Development of smart material－hydraulic pumps and actuators［C］／ASME 2006International Mechanical Engineering Congress and Exposition．Chicago：American Society of Mechanical Engineers，2006：435－443．

［6］ CHAUDHURI A，WERELEY N M．Compact hybrid electro－hydraulic actuators using smart materials：A review［J］．Journal of Intelligent Material Systems and Structures，2012，23（6）：597－634．

［7］ 陈龙，朱玉川，杨旭磊，等．超磁致伸缩泵驱动磁路建模及数值分析［J］．中国机械工程，2014，25（6）：718－722．CHEN L，ZHU Y C，YANG X L，et al．Driving magnetic path modeling and numerical analysis in giant magnetostrictive pump［J］．China Mechanical Engineering，2014，25（6）：718－722（in Chinese）．

［8］ CHAUDHURI A，YOO J H，WERELEY N M．Design，test and model of a hybrid magnetostrictive hydraulic actuator［J］．Smart Materials and Structures，2009，18（8）：085019．

［9］ RUPINSKY M J．Smart material electro－hydrostatic actu－ator for intelligent transportation systems［D］．Ohio：The Ohio State University，2006：15－23．

［10］ 朱玉川，李跃松．射流伺服阀用放大型超磁致伸缩执行器建模与分析 ［J］．航空学报，2014，35（11）：3156－3165．ZHU Y C，LI Y S．Modeling and analysis for amplified giant magnetostrictive actuator applied to jet－pipe electrohydraulic servovalve［J］．Acta Aeronautica et Astronautica Sinica，2014，35（11）：3156－3165（in Chinese）．

［11］ CHAUDHURI A，YOO J H，WERELEY N M，et al．Scaling－up issues with a magnetostrictive－hydraulic pump［C］／ASME 2006International Mechanical Engineering Congress and Exposition．Chicago：American Society of Mechanical Engineers，2006：403－408．

［12］ LI Y S，ZHU Y C，WU H T，et al．Modeling and inverse compensation for giant magnetostrictive transducer applied in smart material electrohydrostatic actuator［J］．Journal of Intelligent Material Systems and Structures，2014，25（3）：378－388．

［13］ JOHN S，SIROHI J，WANG G，et al．Comparison of piezoelectric，magnetostrictive，and electro－strictive hybrid hydraulic actuators［J］．Journal of Intelligent Material Systems and Structures，2007，18（10）：1035－1048．

［14］ KIM G W，WANG K W．Helmholtz resonance in a piezoelectric－hydraulic pump－based hybrid actuator［J］．Smart Materials and Structures，2011，20（1）：015010．

［15］ LARSON J P，DAPINO M J．Design of a smart material electro－hydraulic actuator with improved frequency bandwidth［C］／SPIE Smart Structures and Materials＋ Nondestructive Evaluation and Health Monitoring．Florida：International Society for Optics and Photonics，2012：83430K－1－83430K－9．

［16］ LINDLER J E，ANDERSON E H，REGELBRUGGE M E．Design and testing of piezoelectric－hydraulic actuators［C］／Smart Structures and Materials．Florida：International Society for Optics and Photonics，2003：96－107．

［17］ CADOU C，ZHANG B．Performance modeling of a piezohydraulic actuator［J］．Journal of Intelligent Material Systems and Structures，2003，14（3）：149－160．

［18］ NASSER K，VUJIC N，LEO D J，et al．Modeling and testing of a piezohydraulic actuation system［C］／SPIE’s 8th Annual International Symposium on Smart Structures and Materials．Florida：International Society for Optics and Photonics，2001：354－365．

［19］ OATES W S，LYNCH C S．Piezoelectric hydraulic pump system dynamic model［J］．Journal of Intelligent Material Systems and Structures，2001，12（12）：737－744．

［20］ ZHAO Y P，CHEN D F，LU Q G．The development and application of smart material pumps［J］．Advanced Materials Research，2013，681：260－265．

［21］ XUAN Z，JIN T，SAN H N，et al．Performance of piezostacks for a piezoelectric hybrid actuator by experiments［J］．Journal of Intelligent Material Systems and Structures，2014，25（18）：2212－2220．

［22］ JOHN S，CHAUDHURI A，WERELEY N M．A magnetorheological actuation system－part II：modeling［C］／ASME 2007International Design Engineering Technical Conferences and Computers and Information in Engineering Conference．Chicago：American Society of Mechanical Engineers，2007：249－259．

［23］ 盛敬超．液压流体力学［M］．北京：机械工业出版社，1980：292－304．SHENG J C．Hydro－mechanics［M］．Beijing：China Machine Press，1980：292－304（in Chinese）．

［24］ 王春行．液压伺服控制系统［M］．北京：机械工业出版社，1981：78－83．WANG C H．Hydraulic servo control system ［M］．Beijing：China Machine Press，1981：78－83（in Chinese）．

Experimental investigation and characteristic analysis of a giant magnetostrictive materials－based electro－hydrostatic actuator

YANG Xulei，ZHU Yuchuan＊，JI Liang，FEI Shangshu，GUO Yazi
College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China

Electro－hydrostatic actuators（EHAs）driven by giant magnetostrictive materials（GMM）have some features including highly integrated structure，lots of factors affecting the performance and complex theoretical analysis．In order to search a reliable theoretical analysis method of giant magnetostrictive materials－based electro－hydrostatic actuator（GMEHA）and improving the output performance，the experiment platform of GMA is built in this paper and contrast experiment of actuator dynamic characteristics is completed．On the basis of accurate test and observation of experimental phenomena，structure decomposition of GMEHA is done．Natural frequency of each part is set as breakthrough point of theoretical analysis．A method of combining experiments，theory and finite element analysis（FEA）is taken to analyze the effect on the output performance of actuator caused by dynamic characteristics of cantilever valve，pipeline，hydraulic cylinder and accumulator．The theory analysis method in accordance with experiment is concluded and the key part which affected and restricted the output performance of actuator is determined．Finally，the optimization scheme of GMEHA is put forward on the basis of the above theoretical and experimental researches．Experimental results of actuator after optimization show that the best output performance has been

at the frequency of about 200Hz and the bias of 0．6MPa with the valve of 0．15mm thickness，and the maximum output flow can reach 1．2L／min．

giant magnetostrictive materials；electro－hydrostatic actuator；dynamic characteristics；experimental investigation；output performance；optimization

2015－08－31；Revised：2015－09－17；Accepted：2015－10－30；Published online：2015－11－26 08：29

URL：www．cnki．net／kcms／detail／11．1929．V．20151126．0829．004．html

s：National Natural Science Foundation of China（51575258）；Natural Science Foundation of Jiangsu Province（BK20131359）

V227＋．83；TH137

A

1000－6893（2016）09－2839－12

10．7527／S1000－6893．2015．0295

2015－08－31；退修日期：2015－09－17；录用日期：2015－10－30；网络出版时间：2015－11－26 08：29

www．cnki．net／kcms／detail／11．1929．V．20151126．0829．004．html

国家自然科学基金（51575258）；江苏省自然科学基金（BK20131359）

＊通讯作者．Tel．：025－84892503 E－mail：meeyczhu＠nuaa．edu．cn

杨旭磊，朱玉川，纪良，等．超磁致伸缩电静液作动器的试验研究与特性分析［J］．航空学报，2016，37（9）：28392－850．YANG X L，ZHU Y C，JI L，et al．Experimental investigation and characteristic analysis of a giant magnetostrictive materialsbased electroh－ydrostatic actuator［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：28392－850．

杨旭磊 男，硕士研究生。主要研究方向：智能材料及其结构，电液伺服控制技术。

E－mail：qdyangxl＠163．com

朱玉川 男，博士，副教授。主要研究方向：智能材料及其结构，电液伺服控制技术。

Tel．：025－84892503

E－mail：meeyczhu＠nuaa．edu．cn

＊Corresponding author．Tel．：025－84892503 E－mail：meeyczhu＠nuaa．edu．cn