远场假设对喷流噪声预测中格林函数求解的影响

徐希海，李晓东＊

北京航空航天大学能源与动力工程学院，北京 100083

远场假设对喷流噪声预测中格林函数求解的影响

徐希海，李晓东＊

北京航空航天大学能源与动力工程学院，北京 100083

目前基于雷诺平均Navier－Stokes（RANS）的喷流噪声预测方法在格林函数求解时，为简化求解过程，通常对喷流流动做平行流假设，对观测点做远场假设。随着格林函数求解方法发展，近年来的研究表明平行流假设对下游观测点格林函数的计算会引起较大偏差，而目前远场假设对格林函数求解的影响仍不清楚。为研究远场假设对喷流格林函数求解的影响，以二维喷流为例，采用计算气动声学方法（CAA）分别数值求解了观测点远场假设条件与实际条件下90°～150°方向喷流内伴随格林函数，进而分析远场假设对格林函数求解的影响。研究结果表明，对于不同方向的观测点，由观测远场假设导致的伴随格林函数求解偏差不尽相同，且对于越靠近喷流中心线方向的观测点，远场假设导致的偏差越大，其中150°方向观测点，采用远场假设后，格林函数计算结果最大偏差达到－15dB以上。因此，对于靠近喷流中心线方向的噪声观测点而言，为避免预测偏差，应采用实际观测条件求解喷流格林函数。

气动声学；剪切流；散射波；格林函数；伴随方法；计算流体力学；计算气动声学

自19世纪中期以来，Lighthill［1－2］提出的声类比理论在很长时间内都是喷流噪声预测的主流理论。其最突出的贡献在于Lighthill通过Navier－Stokes方程重组将噪声源和声传播在方程中独立开来。在基于声类比理论的预测方法中，方程右边的声源项通过实验结果或数值结果结合模化函数获得，而噪声传播过程则通过格林函数描述。因此声源模化和格林函数求解是声类比预测方法的两个关键环节。

Lighthill方程左边为波动算子，其格林函数是自由空间格林函数，不能考虑声波与流动的相互作用，且Lighthill方程右边声源项包含太多非真实声源信息。众多研究者一直试图改进Lighthill方程，提出了 Pridmore－Brown方程［3］、Phillips方程［4］和Lilley方程等，其中又以Lilley方程应用最为广泛。Lilley方程将声的输运项及散射项移至方程左边波动算子中，获得更趋实际的控制方程。虽然Lilley方程可以考虑声波在流动中的散射效应，但面对复杂流动问题Lilley方程格林函数不能获得理论解。因此在喷流噪声预测方法中，由于喷流流动的复杂性，如何准确求解喷流内格林函数一直是喷流噪声预测中的关键问题。

Mani［5］将喷流简化为完全平行流动，并对观察点做远场假设，给出了喷流内Lilley方程格林函数的近似解，并以此为基础，结合CFD得出的湍流平均信息发展了计算喷流噪声的MGB程序。Goldstein［6］对轴对称喷流做平行流简化，给出了低频多点声源的格林函数。Balsa［7］和 Goldstein［8］分别给出了非轴对称喷流平行流假设下的高频格林函数的近似解。对于特别高频的声音，波长很短，格林函数可以采用几何声学的方法计算，这种方法由Schubert［9］提出。Durbin［10］建立了几何声学的普适理论。Khavaran和 Krejsa［11－14］将几何声学的方法应用于非平行流、非轴对称喷流的格林函数计算，给出了近似解，并用该格林函数近似解结合改进的声源模化函数改进了MGB方法，使其演变为MGBK喷流噪声预测方法。

由于格林函数求解方法的制约，早期喷流格林函数求解通常通过平行流假设和观测点远场假设获得近似解。随着求解方法的发展，Tam和Auriault［15］在1998年将伴随方法应用到喷流噪声格林函数的计算中。采用计算气动声学（CAA）方法求解了非平行流下喷流内格林函数，并与平行流假设下格林函数结果对比。其结论表明针对喷流下游方向观测点的喷流格林函数采用平行流假设会造成较大误差，因此不能采用平行流假设。1999年，Tam和Auriault在伴随格林函数求解方法的基础上发展了喷流小尺度湍流噪声预测方法（TA方法），由于该方法主要针对与喷流方向垂直的边线噪声预测，因此在TA方法格林函数求解中仍然采用平行流假设及远场假设［16－17］。2002年，Tam 和Auriault采用TA 方法预测了矩形喷管噪声，在求解格林函数时沿用了平行流假设及远场假设。近年来，Frate［18］、Cheung［19］、Simmons［20］以及 Xu［21］等在采用基于雷诺平均Navier－Stokes（RANS）方程的喷流噪声预测方法预测不同喷管的喷流噪声中，格林函数求解时均沿用了平行流假设及远场假设。2011年，Karabasov等［22］研究发现是否采取平行流假设对低频噪声格林函数有较大影响，对远场频谱最大有近8dB的影响。2012年，Goldstein等［23］研究验证了Karabasov等对于喷流低频噪声的准确格林函数计算则必须采用真实非平行流计算的观点。Tam［15］、Karabasov［22］及 Goldstein［23］等 针对平行流假设对于格林函数的影响进行了较为完善的研究，然而为了简化计算，他们在研究中对远场观测点仍然采用了远场无穷远假设。

而实际实验测试中观测点不可能位于无穷远，通常定位在距离喷管出口中心的100D处（D为喷管当量直径）。无论是圆形喷管还是矩形喷管，相对喷流剪切方向尺寸而言，100D可以认为足够远，然而由于喷流的流动方向尺寸远大于剪切方向尺寸，通常能超过30D。当观测点与喷流流向夹角较小时，观测点与喷流中心线的距离将与喷流的流向尺寸相当，此时对观测点采用远场假设求解格林函数则可能引起偏差。而目前远场假设对喷流噪声预测中格林函数求解影响仍不清楚。因此本文以二维喷流为例，采用CAA方法分别数值求解了观测点在实际条件及远场假设条件下不同观测角度时喷流内的伴随格林函数，并对比分析了远场假设对格林函数计算结果的影响。

1 伴随格林函数理论

由于喷流流动中存在着强烈的剪切层，如图1所示，喷流噪声向远场传播时，穿过剪切层将会发生散射现象，从而影响远场指向性分布。如何准确计算这种散射效应的影响，是喷流远场噪声预测中的关键问题之一。

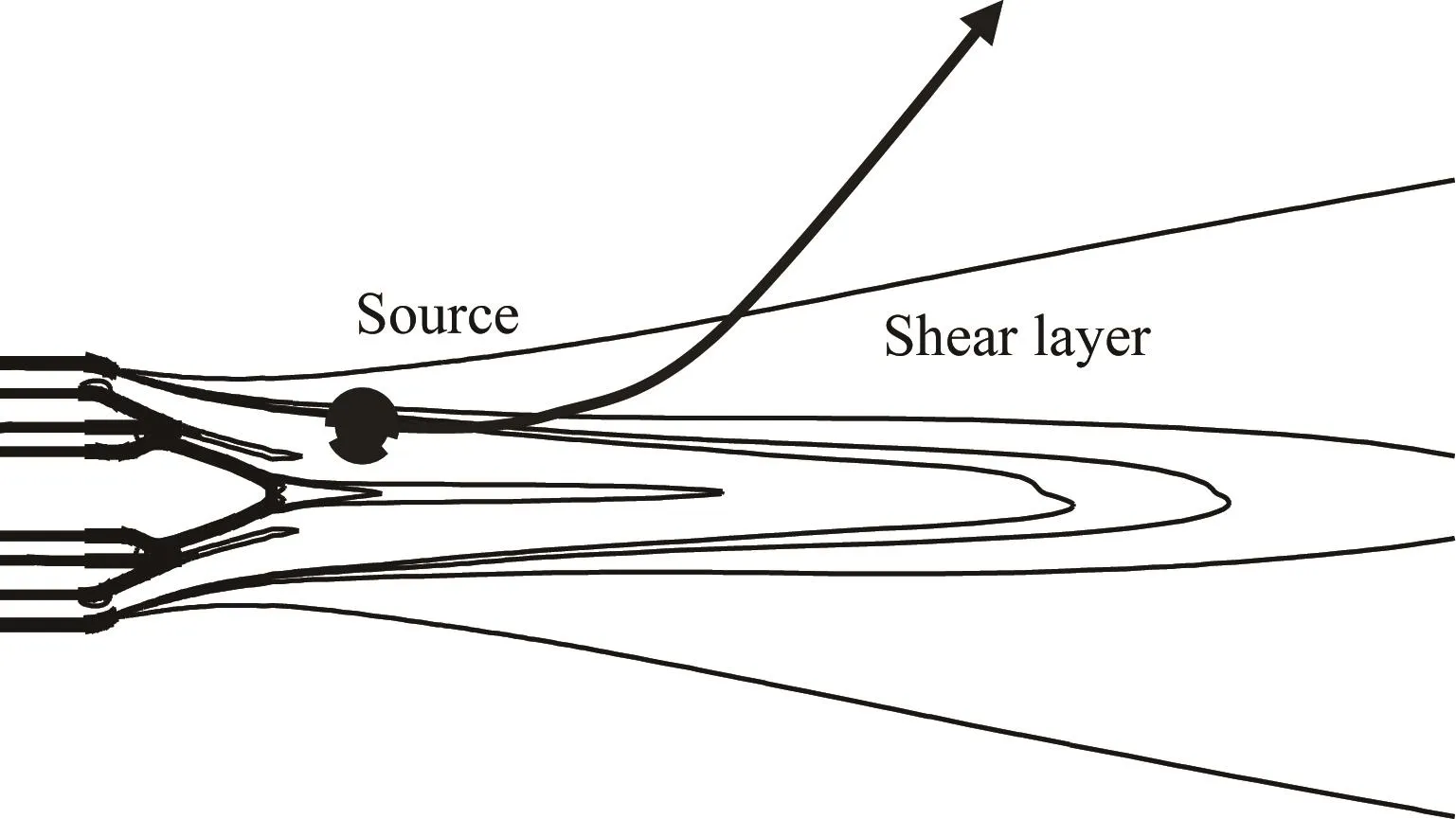
图1 喷流噪声穿过剪切层发生散射现象Fig．1 Noise refraction going through jet shear layer

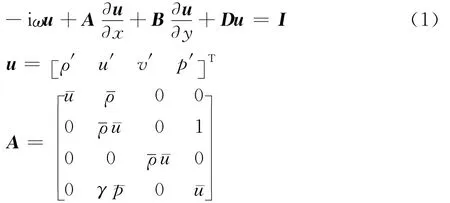
相比于波动方程，线化欧拉方程可以描述声波在流动中的传播过程，更适合作为喷流中声传播的主控方程。方程式（1）是笛卡儿坐标下频域内的二维线化欧拉方程。

式中：i表示虚部；ω 为角频率；ρ′、u′、v′和p′分别为脉动密度、脉动速度及脉动压力和则分别为喷流平均密度、平均速度及平均压力；方程右边的Q1、Q2分别为x、y方向的动量源项，即声源项。

在喷流噪声预测中，假定喷流声源都是相互独立的不相干声源，因此可以采用格林函数的方法描述噪声在流动中的散射现象，进而预测远场噪声。上述带源项的线化欧拉方程式（1）对应的格林函数为

由于方程式（1）中两个动量方程右边均存在声源项，因此这里格林函数分为两组，以上标n区分 。xs为声源点坐标，ω0为声源频率。

式（2）描述的是声波在经过剪切层散射的过程，方程右边的源项为δ函数。这意味着在格林函数计算中每一个声源点都是奇异点。如图2所示，如果想求解每一个声源点xs到观测点xo的格林函数G（n）（xs，xo），由于喷流中每个点都是声源点，因此针对每一个声源点都要求一遍方程式（2）才能求得关于该声源的格林函数，这给求解带来了极大的困难。

如图3所示，将声源点与观测点调换位置，观测点到声源点的格林函数记为（xo，xs），为G（n）（xs，xo）的伴随格林函数。在不存在流动的情形下满足方程式（3），二者相等，即在无流动的情形下线化欧拉方程为自伴随方程。

图2 直接声散射问题Fig．2 Direct sound radiation problem

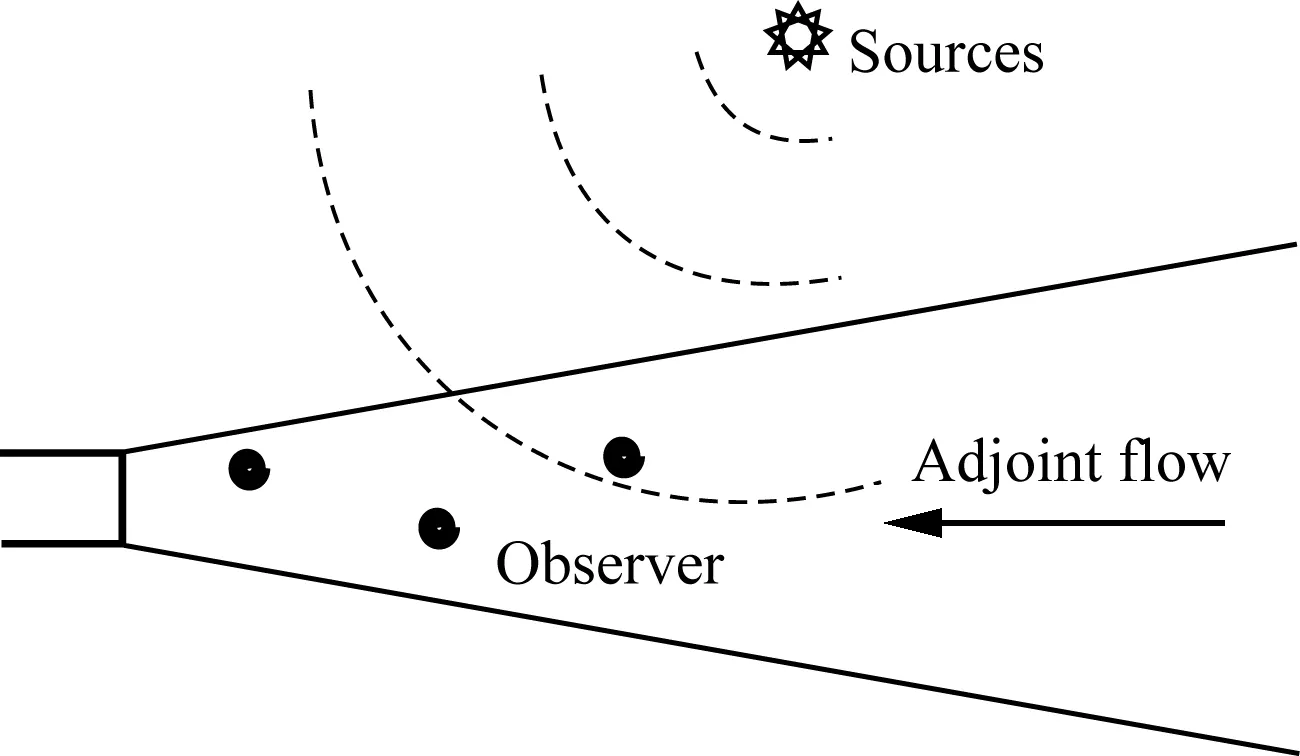
图3 伴随问题Fig．3 Adjoint problem

如图2和图3所示，存在喷流流动情形下的线化欧拉方程并非自伴随方程。但可以构建如方程式（4）［15］所示的伴随格林方程使其满足方程式（3）。这样可以通过求解伴随方程式（4）进而得出方程式（2）中的格林函数G（n）。

由于观测点x0在喷流之外，在伴随格林函数的计算中只有x0这一个奇异点，因此只要一次计算就可以得到所有声源点的伴随格林函数，极大地简化了计算过程。

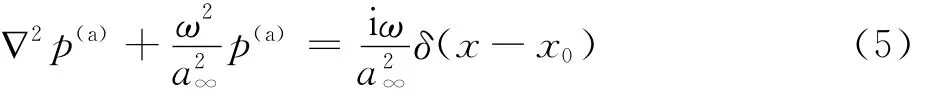
方程式（5）的理论解［17］为

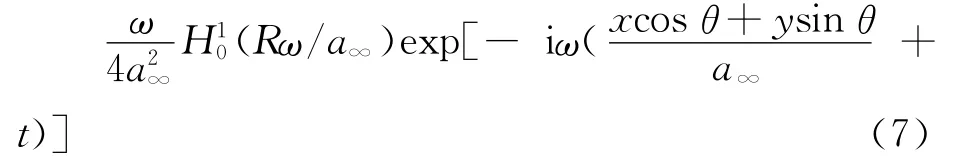
如图4所示，将观测点位置做远场无穷远假设后，伴随入射波简化为平面波。简化给计算带来便利的同时也会对格林函数的计算精度带来影响。尤其当观测点与喷流流向夹角较小时，观测点与喷流中心线的距离将与喷流的流向尺寸相当，此时采用无穷远假设求解格林函数则可能引起偏差。

图4 远场假设（平面入射波）Fig．4 Far field assumption（plane incoming wave）

2 平均流场计算

式中：T为喷流入口温度；T∞为环境温度；Maj为喷流出口马赫数。

本文的喷流流场采用商用软件Fluent计算，Thies和Tam研究［24］表明标准k－ε模型不能够准确模拟喷流流动。为准确获得喷流平均流场，本文在计算中采用Thies和Tam根据喷流实验数据系数改进的带有Pope ＆Sarkar修正系数的k－ε 湍 流 模 型［25－27］。 其 中 湍 流 模 型 的 系 数 为：σk＝0．324，σε＝0．377，α1＝0．518，cμ＝0．087 4，cε1＝1．4，cε2＝2．02，PT＝0．422，cε3＝0．822。

图5为喷流沿x方向的速度等值线图，并给出了喷流下游的流动发展及速度分布。横坐标x为喷流轴向坐标，纵坐标r为喷流径向坐标。

图5 喷流x方向的速度等值线图Fig．5 Contour of xaxis velocity lines

3 声场数值计算方法

由于喷流流场的存在，伴随格林函数方程式（4）必须采用数值求解方法。数值计算中为了降低计算量，将观测点（在伴随方程中的声源点）放在计算域之外，声源点产生的声波以入射波的形式进入，如图6所示的计算域，PML表示完全匹配层边界条件。本文计算域的x方向范围为（－2D，85D），y方向范围为（－18D，18D）。观测点定义在距离喷管出口中心R＝100D处，观测角度在θ＝90°～150°方向。喷流流场数据取自上文的RANS计算结果。

图6 格林函数计算域及边界条件Fig．6 Computational domain and boundary condition

伴随格林函数中声源点在计算域外避免了计算中声源点奇异的问题。声源点产生的声波以入射波的形式进入，因此本文中对方程式（4）采取入射波声散射方法求解，数值计算中将伴随格林函数分为入射波和散射波两个部分，即

式中：Gin为入射波；G′为散射波。因此方程式（2）的算子形式可以转换为

L为方程式（2）中的格林函数算子，将入射波移到方程右边作为声源项则得到关于散射波的主控方程：

喷流计算域外由于没有流动，由伴随声源产生的入射声波可以通过理论解得到。实际条件下，伴随声源产生的入射波为

如果对观测点做远场无穷远假设，R→∞时，方程式（12）可以简化方程式（13），H10为0阶的第一类Hankel函数。

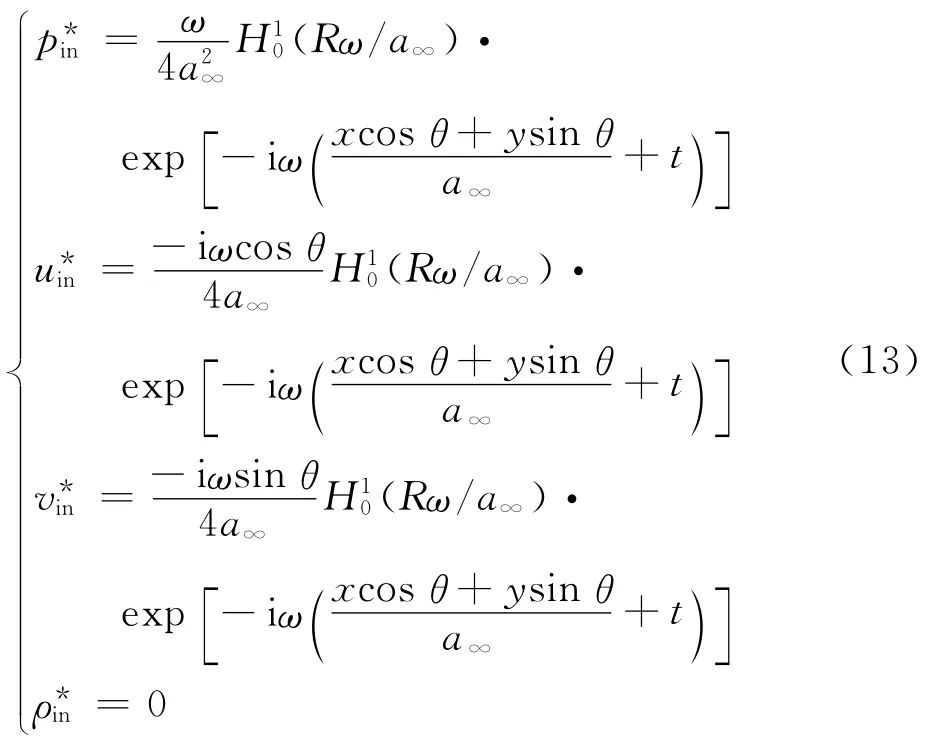
入射波以声源的形式加在边界上，因此数值计算中无反射边界条件必须在吸收散射声波的同时不能吸收入射声波。如图6所示，计算域四周采用采用Hu［28］发展的完全匹配层边界条件，边界层网格为正交网格。计算中在PML吸收区域内将声波分为入射波和散射波两个部分，只针对散射波的PML边界条件为

式中：

数值计算中空间差分采用频散相关保持格式（DRP）［29］，时间推进采用四阶精度优化的低频散、低耗散龙格库塔格式［30］。

4 网格收敛性验证

为了开展网格收敛性研究，生成了粗、中、细3套网格用于喷流伴随格林函数的数值计算。计算域及中网格分布如图7所示。表1给出了3套网格的基本参数。为了准确模拟声波在剪切层中的散射效应，对剪切层区域进行了网格加密处理。

图7 计算域及网格Fig．7 Computational domain and grid

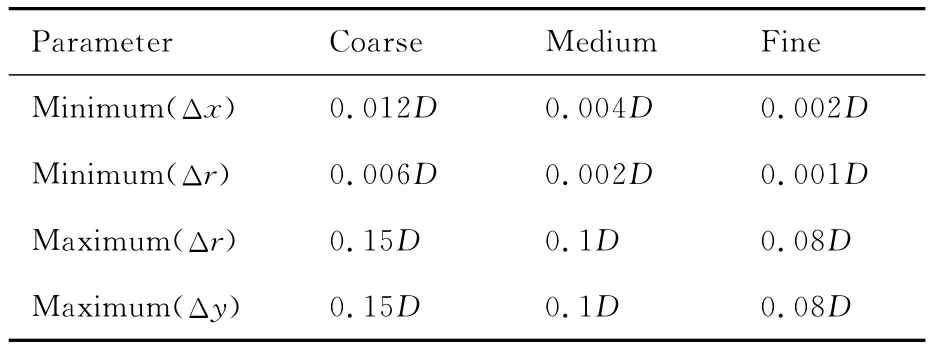
表1 数值计算采用的网格参数Table 1 Grid parameters for numerical calculation

图8给出了中网格时，柱面入射波下，下游135°方向观测点对应的喷流伴随格林函数云图。同时在图9给出了3种不同粗细网格在中心线上（r＝0）沿x方向喷流伴随格林函数（ω，x）的分布。结果表明粗网格的计算结果在喷流核心区前部（x＜10D）结果稍微偏小，在核心区以后的局域与中网格及细网格结果吻合较好。这与剪切层里的网格密度相关，过粗网格在描述剪切层速度梯度时存在误差。中网格与细网格的计算结果在中心线上各处均具有很好的一致性。

图8 柱面伴随入射波下θ＝135°方向观测点对喷流内伴随格林函数结果云图Fig．8 Contour of adjoint Green’s function for observers atθ＝135°under cylindrical incoming wave

图9 柱面伴随入射波下中心线上（r＝0）伴随格林函数分布Fig．9 Adjoint Green’s function distribution at center line（r＝0）under plane incoming wave

图10给出了中网格时，平面入射波下，下游135°方向观测点对应的喷流伴随格林函数云图。同时在图11则给出了3种不同粗细网格在中心线上（r＝0）沿x方向喷流伴随格林函数（ω，x）的分布。粗、中、细3种网格的计算表现与柱面入射波时相似。中网格与细网格的计算结果在中心线上各处均具有很好的一致性，因此可以认为中网格以达到网格无关性要求。

图10 平面伴随入射波下θ＝135°方向观测点对喷流内伴随格林函数结果云图Fig．10 Contour ofadjoint Green’s function for observers atθ＝135°under plane incoming wave

图11 柱面伴随入射波下中心线上（r＝0）伴随格林函数分布Fig．11 Adjoint Green’s function distribution at center line（r＝0）under plane incoming wave

5 计算结果与分析

图 12 为 90°、105°、120°、135°、140°、145°和150°方向观测点频域伴随格林函数（ω，x）的计算结果云图。喷流湍流混合噪声峰值频率斯特劳哈尔数（St＝fD／U）通常在0．2～1．0之间，Tam和Auriaul给出的实验结果表明马赫数0．9的冷喷流在边线处远场声压频谱峰值频率的斯特劳哈数St接近0．5，因此在本文中取St＝0．5研究远场假设对格林函数求解的影响。图中黑色实线是珔u＝uj的速度等值线，表征喷流核心区位置，同时喷流噪声源也被认为在喷流核心区附近。图12（a）是观测点远场假设条件下，以平面伴随声波入射喷流区域的计算结果；图12（b）是观测点实际条件下，以伴随柱面声波入射喷流区域的计算结果。从图12可以看出，由于喷流流动的影响，无论是平面入射波还是柱面入射波，伴随格林函数（ω，x）从边线90°方向到下游150°方向经历了从小增大又减小的过程，这与喷流噪声指向性是一致的。

下游105°方向观测点对应的喷流伴随格林函数云图与90°方向的格林函数云图相比，由于喷流流动的存在，喷流区域的格林函数明显增强。观测点远场假设与实际条件下105°方向喷流伴随格林函数（ω，x）云图对比来看，观测点远场假设与实际条件的格林函数计算在整个区域的幅值上较为接近，但格林函数的分布并不相同。与实际观测点条件下柱面入射波的计算结果相比，观测点远场假设下平面入射波的伴随格林函数增强的区域在喷流下游分布更广。这表明对于这些区域，采用远场假设计算的格林函数不准确，用于预测噪声可能会引起误差。

下游120°方向观测点对应喷流伴随格林函数云图与105°方向的格林函数云图相比，由于剪切层散射的影响，120°方向观测点的格林函数更大。观测点远场假设与实际条件下120°方向喷流伴随格林函数（ω，x）云图对比来看，观测点远场假设与实际条件的格林函数计算在整个区域的分布较为接近。但在整个流动区域，与实际观测点条件下柱面入射波的计算结果相比，下游120°方向观测点远场假设下平面入射波的伴随格林函数要明显大于不做远场假设的柱面入射波的格林函数。这表明对于下游120°方向的喷流格林函数计算，采用远场假设会导致格林函数计算结果偏大。

下游135°方向观测点的喷流伴随格林函数云图与120°方向的格林函数云图相比，伴随格林函数的峰值位置向喷流下游移动。观测点远场假设与实际条件下135°方向喷流伴随格林函数云图对比可以看出，在柱面入射波下，135°方向与120°方向相比，在整个喷流流动区域，伴随格林函数继续增大。

下游140°方向观测点在远场假设下平面入射波计算结果与135°方向的计算结果相比，整个喷流流动区域的格林函数开始变小。而140°方向观测点实际条件下柱面入射波的格林函数计算结果在整个喷流流动区域仍然维持在比较大的数值。在整个流动区域，柱面入射波的格林函数都要大于平面入射波的格林函数。这表明在140°方向，如果采用远场假设计算格林函数会导致计算结果偏小。

下游145°方向观测点在远场假设下平面入射波计算结果与140°方向的计算结果相比，整个喷流区域的格林函数进一步变小。145°与140°方向的观测点实际条件下柱面入射波计算结果相比，在145°方向整个喷流流动区域的格林函数也开始降低。而在整个流动区域，柱面入射波的格林函数都要大于平面入射波的格林函数。这表明在145°方向，如果采用观测点远场假设计算格林函数会导致计算结果偏小。

下游150°方向观测点在远场假设下平面入射波计算结果与145°方向的计算结果相比，整个喷流区域的格林函数进一步变小。150°与145°方向的观测点实际条件下柱面入射波计算结果相比，在150°方向整个喷流流动区域的格林函数也进一步降低。而在整个流动区域，柱面入射波的格林函数都要大于平面入射波的格林函数。这表明在150°方向，如果采用观测点远场假设计算格林函数会导致计算结果偏小。

图12 θ＝90°～150°方向观测点对喷流内伴随格林函数（（ω，x））结果云图Fig．12 Contour of adjoint Green’s function（（ω，x））of jet flow for observers atθ＝90°－150°

由于喷流噪声主要集中在喷流核心区附近，本文选择喷流内不同位置的3点A、B、C。针对不同远场观测点的伴随格林函数进行进一步对比分析。A、B、C 的位置如图13所示，分别是A（2D，0），B（6D，0），C（10D，0）。

图14是观测点远场无穷远假设下，以平面伴随入射波计算的A、B、C3点针对各个方向观测点的伴随格林函数的对比图，为使对比更为直观，纵坐标中选取pe＝10－5Pa。从图中可以看出，对于90°、105°、120°这3个远场观测方向而言，喷流内A、B、C3点的伴随格林函数几乎相同。在下游135°方向，3点的伴随格林函数均达到最大值，且C点的伴随格林函数最大，A点伴随格林函数最小。从135°方向到150°方向，3点的格林函数均呈现直线降低趋势。

图13 A、B、C3点的位置Fig．13 Position of three different points A、B、C

图14 远场假设下A、B、C3点的伴随格林函数（ω，x）Fig．14 Adjoint Green’s function（ω，x）of A，B，C points with farfield assumption

图15是在无远场假设条件下，以柱面伴随入射波计算的A、B、C3点针对各个方向观测点的伴随格林函数的对比图。从图中可以看出，对于90°、105°、120°这3个远场观测方向而言，喷流内A、B、C3点的伴随格林函数的格林函数有微弱差别。与远场假设平面声波入射时不同，这里A、B、C3点格林函数的峰值并不在同一方向。其中A点的格林函数峰值出现在135°方向，B点的格林函数峰值出现在135°～140°之间，C点格林函数峰值则出现在140°方向。这意味这3点声源发出的噪声经过喷流剪切层后散射后的远场指向性并不一样，但如图14所示，在采取远场假设后，各点指向性的区别则不能计算出来。

图15 无远场假设下A、B、C3点的伴随格林函数（ω，x）Fig．15 Adjoint Green’s function（ω，x）of A，B，C without farfield assumption

图16（a）是喷流内A点对不同远场点的格林函数对比曲线，其中实线是观测点做远场假设时的计算结果，虚线则是实际条件下的计算结果。在90°、105°、120°、135°方向，远场假设平面入射波的伴随格林函数的计算结果略大于实际柱面入射波下的计算结果，约2dB，且呈现一定规律性。在140°～150°方向，远场假设平面入射波的伴随格林函数的计算结果在135°达到峰值后，在向更下游方向快速降低。而实际条件下柱面入射波的结果在到达峰值方向后，降低趋势较为平缓。在140°～150°方向远场假设的计算结果小于实际观测条件下的计算结果，且越向喷流中心线方向差距越大。在150°方向，对于A点有近8dB的差别。

图16（b）所示是喷流内B点对不同远场点的格林函数对比曲线，其中实线是观测点做远场假设时的计算结果，虚线则是实际条件下的计算结果。在90°、105°、120°、135°方向，远场假设平面入射波的伴随格林函数的计算结果略大于实际柱面入射波下的计算结果，约2dB，呈现一定规律性。在140°～150°方向，远场假设平面入射波的伴随格林函数的计算结果在达到峰值后，在向更下游方向快速降低。而实际条件下柱面入射波的结果在到达峰值方向后，降低趋势较为平缓。在135°～150°方向远场假设的计算结果小于实际条件下的计算结果，且越向喷流中心线方向差距越大。在150°方向，对于A点有近11dB的差别。

图16 不同入射波下伴随格林函数（ω，x）对比Fig．16 Comparison of adjoint Green’s function（ω，x）with different incoming wave

图16（c）是喷流内C点对不同远场点的格林函数对比曲线，其中实线是观测点做远场假设时的计算结果，虚线则是实际条件下的计算结果。在90°、105°、120°、135°方向，远场假设平面入射波的伴随格林函数的计算结果略大于实际柱面入射波下的计算结果，约3dB，呈现一定规律性。在140°～150°方向，远场假设平面入射波的伴随格林函数的计算结果在140°方向达到峰值后，在向更下游方向快速降低。而实际条件下柱面入射波的结果在到达峰值方向后，降低趋势较为平缓。在140°～150°方向远场假设的计算结果小于实际条件下的计算结果，且观测点越靠近喷流中心线方向偏差越大越大。在150°方向，对于A点有近15dB的差别。

综合上述结果，在90°～135°方向，观测点远场假设格林函数的计算结果相比实际条件的格林函数计算结果约稍大1～3dB。在135°以后，由于喷流剪切层对该方向的声波有极强的散射作用，远场假设会导致伴随格林函数计算结果偏小，且对越靠近中心线方向的观测点，远场假设导致的偏差越大。而且对越下游的声源点，远场假设导致的计算偏差也越大。因此，对于靠近喷流中心线方向的噪声观测点而言，为减小预测偏差，在格林函数求解时应避免采用观测点远场假设。

6 结 论

1）在垂直于喷管出口的90°方向，由于此方向声波传播与流动方向垂直，因此声传播受流动影响较小，远场远假设下格林函数计算结果与实际条件下的计算结果几乎一致。因此90°方向观测点的格林函数求解可以采用远场假设简化求解过程。

2）在喷流下游105°～135°方向，由于喷流剪切层对声波的散射效应，远场假设格林函数计算结果与实际条件的计算结果相比存在0～3dB的偏差。

3）在喷流下游140°～150°方向，由于喷流剪切层在该方向对噪声辐射的强烈影响，观测点远场假设的格林函数计算结果与实际条件下的计算结果相比存在明显偏差。而且结果表明对越靠近中心线方向的观测点，远场假设导致的计算偏差越大。对于150°方向观测点，采用远场假设后，格林函数计算结果最大偏差在－15dB以上。而且对越下游的声源点，远场假设导致的计算偏差也越大。因此，对于靠近喷流中心线方向的噪声观测点而言，为避免产生预测偏差，应采用实际观测条件求解喷流格林函数。

4）与二维喷流相比，在相同马赫数下三维喷流的核心区略短于二维喷流。但二维喷流与三维喷流均存在强烈的剪切层，具有相似的剪切及流动特征，以及流动方向尺度均远大于剪切方向尺寸的基本特征。对于二维喷流而言，流动方向尺度均远大于剪切方向尺寸是导致采用远场假设计算格林函数在下游出现偏差的原因。对于三维喷流，流动方向尺度同样远大于剪切方向的尺寸，采用远场假设求解可能出现与二维喷流类似的偏差。因此对于三维喷流，远场假设对格林函数求解的影响值得进一步研究。

［1］ LIGHTHILL M J．On sound generated aerodynamically．I．General theory［J］．Proceedings of the Royal Society A，1952，211：564－587．

［2］ LIGHTHILL M J．On sound generated aerodynamically．Part II．Turbulence as a source of sound［J］．Proceedings of the Royal Society A，1954，222：1－34．

［3］ PRIDMORE－BROWN D C．Sound propagation in a fluid flowing through an attenuating duct［J］．Journal of Fluid Mechanics，1958，4（4）：393－406．

［4］ PHILLIPS O M．The intensity of aeolian tones［J］．Journal of Fluid Mechanics，1956，1（6）：607－624．

［5］ MANI R．The influence of flow on jet noise［J］．Journal of Fluid Mechanics，1976，73：753－793．

［6］ GOLDSTEIN M E．The low frequency sound from multiple sources in axisymmetric shear flows［J］．Journal of Fluid Mechanics，1975，70：595－604．

［7］ BALSA T F．The farfield of high frequency convected singularities in sheared flows with anapplication to jet noise prediction［J］．Journal of Fluid Mechanics，1976，74（2）：193－208．

［8］ GOLDSTEIN M E．High frequency sound emission from moving point multiple sources embedded in arbitrary transversely sheared mean flows［J］．Journal of Sound Vibration，1982，80：499－522．

［9］ SCHUBERT L K．Numerical study of sound refraction by ajet flow．I．Rayacoustics［J］．Journal Acoustic Society of America，1972，51：439－446．

［10］ DURBIN P A．High frequency Green’s function for aerodynamic noise in movingmedia［J］．Journal of Sound Vibration，1983，91（4）：519－525．

［11］ KHAVARAN A．Refraction and shielding of noise in non－axisymmetric jet：AIAA－1996－1780［R］．Reston：AIAA，1996．

［12］ KHAVARAN A，KREJSA E A．Propagation of high frequency jet noise using geometric acoustics：AIAA－1993－0147［R］．Reston：AIAA，1993．

［13］ KHAVARAN A，KREJSA E A．Refraction of high frequency noise in an arbitrary jet flow：AIAA－1994－0139［R］．Reston：AIAA，1994．

［14］ KHAVARAN A，KREJSA E A．On the role of anisotropy in turbulent mixing noise：AIAA－1998－2289［R］．Reston：AIAA，1998．

［15］ TAM C K W，AURIAULT L．Mean flow refraction effects on sound radiated from localized sources in a jet［J］．Journal of Fluid Mechanics，1998，370：149－174．

［16］ TAM C K W，AURIAULT L．Jetmixing noise from finescale turbulence［J］．AIAA Journal，1999，37（2）：145－153．

［17］ TAM C K W，PASTOUCHENKO N N．Noise from finescale turbulence of nonaxisymmetric jets［J］．AIAA Journal，2002，40（3）：456－464．

［18］ FRATE F，KHAVARAN A．Anaerodynamic and acoustic assessment of convergent－divergent nozzles with chevrons：AIAA－2011－0976［R］．Reston：AIAA，2011．

［19］ CHEUNG L，PASTOUCHENKO N，MANI R，et al．Fine－scale turbulent noise predictions from non－axisymmetric jet：AIAA－2013－2037［R］．Reston：AIAA，2013．

［20］ SIMMONS S P，HENDERSONAND B，ABBAS KHAVARAN A．Flow field and acoustic predictions for three－stream jets：AIAA－2014－3741［R］．Reston：AIAA，2014．

［21］ XU X H，HE J Y，LI X D，et al．3－D jet noise prediction for separate flow nozzles with pylon interaction：AIAA－2015－0512［R］．Reston：AIAA，2015．

［22］ KARABASOV S A，BOGEY C，HYNES T P．Computation of noise of initially laminar jets using a statistical approach for the acoustic analogy：Application and discussion：AIAA－2011－2929［R］．Reston：AIAA，2011．

［23］ GOLDSTEIN M E，ADRIAN S，AFSAR M Z．Effect of non－parallel mean flow on the Green＇s function for predicting the low－frequency sound from turbulent air jets［J］．Journal of Fluid Mechanics，2012，695：199－234．

［24］ THIES A T，TAM C K W．Computation of turbulent axisymmetric and nonaxisymmetric jet flows using the K－e model［J］．AIAA Journal，1996，34（2）：309－316．

［25］ POPE S B．An explanation of the turbulent round－jet／plane－jet anomaly［J］．AIAA Journal，1978，16（3）：279－281．

［26］ SARKAR S，LAKSHMANAN B．Application of a Reynolds stress turbulence model to the compressible shear layer［J］．AIAA Journal，1991，29（5）：743－749．

［27］ SARKAR S，ERLEBACHER G，HUSSAINI M Y，et al．The analysis and modeling of dilatational terms in compressible turbulence：NASA CR181959［R］．Washington，D．C．：NASA，1989．

［28］ HU F Q．A stable perfectly matched layer for linearized Euler equations in unsplit physical variables［J］．Journal of Computational Physics，2001，173（2）：455－480．

［29］ TAM C K W，WEBB J C．Dispersion－relation－preservingfinite difference schemes for computational acoustics［J］．Journal of Computational Physics，1993，107 （2）：262－281．

［30］ HU F Q，HUSSAINI M Y，MANTHEY J L．Low－dissipation and low－dispersion Runge－Kutta schemes for computational acoustics［J］．Journal of Computational Physics，1996，124（1）：177－191．

Effect of farfield assumption on calculation of Green’s function for predicting jet noise

XU Xihai，LI Xiaodong＊
School of Energy and power engineering，Beihang University，Beijing 100083，China

To simplify the solution procedure of Green’s function，most popular Reynolds－averaged Navier－Stokes（RANS）based jet noise prediction methods suggest to make the assumption that the jet flow is parallel and the observers are located at the infinity farfield．With the development of the solution method of Green’s function，the effect of parallel flow assumption on calculation of the Green’s function has been studied recently．However，the effect of farfield assumption on calculation of the Green’s function has not yet been studied．To study the effect of farfield assumption，the adjoint method is used to calculate the Green’s function in this paper．For actual observer 90°－150°and assumed farfield observer，the adjoint Green’s functions are solved separately by a computational aeroacoustics（CAA）method．Comparison of calculation results of Green’s function for actual observer and for assumed farfield observer are given in this paper．It is found that for different observation angle，the calculated deviation caused by farfield assumption is different．It is also found that there is a greater derivation of calculation results of Green’s function to the point farther away from the nozzle exit．For the observer at 150°，the deviations of calculation results of Green’s function caused by farfield assumption at some point are as large as－15dB．Consequently，for observers close to the jet axis，calculation of adjoint Green’s function should avoid farfield assumption to reduce the prediction error．

aeroacoustics；shear flow；refraction waves；Green’s function；adjoint technique；computational fluid dynamics；computational aeroacoustics

2016－01－13；Revised：2016－04－08；Accepted：2016－04－25；Published online：2016－06－03 13：55

URL：www．cnki．net／kcms／detail／11．1929．V．20160603．1355．002．html

s：National Key Basic Research Program of China （2012CB720201）；National Natural Science Foundation of China（51476005）

V231．1

A

1000－6893（2016）09－2699－12

10．7527／S1000－6893．2016．0127

2016－01－13；退修日期：2016－04－08；录用日期：2016－04－25；网络出版时间：2016－06－03 13：55

www．cnki．net／kcms／detail／11．1929．V．20160603．1355．002．html

国家“973”计划（2012CB720201）；国家自然科学基金（51476005）

＊通讯作者．Tel．：010－82318579 E－mail：lixd＠buaa．edu．cn

徐希海，李晓东．远场假设对喷流噪声预测中格林函数求解的影响［J］．航空学报，2016，37（9）：26992－710．XU X H，LI X D．Effect of farfield assumption on calculation of Green’s fanction for predicting jet noise［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：26992－710．

徐希海 男，博士研究生。主要研究方向：气动声学、喷流噪声、计算流体力学。

E－mail：xuxihai＠buaa．edu．cn李晓东 男，博士，教授。主要研究方向：气动声学、计算气动声学、流体力学。Tel．：010－82318579 E－mail：lixd＠buaa．edu．cn

＊Corresponding author．Tel．：010－82318579 E－mail：lixd＠buaa．edu．cn