On the gating of mechanosensitive channels by fluid shear stress
Zhangli Peng·On Shun Pak·Zhe Feng·Allen P.Liu·Yuan-Nan Young
On the gating of mechanosensitive channels by fluid shear stress
Zhangli Peng1·On Shun Pak2·Zhe Feng1·Allen P.Liu3·Yuan-Nan Young4
©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016
Mechanosensation is an important process in biological fluid–structure interaction.To understand the biophysics underlying mechanosensation,it is essential to quantify the correlation between membrane deformation, membrane tension,external fluid shear stress,and conformation of mechanosensitive(MS)channels.Smoothed dissipative particle dynamics(SDPD)simulations of vesicle/cell in three types of flow configurations are conducted to calculate the tension in lipid membrane due to fluid shear stress from the surrounding viscous flow.In combination with a simple continuum model for an MS channel,SDPD simulation results suggest that shearing adhered vesicles/cells is more effective to induce membrane tension sufficient to stretch MS channels open than a free shear flow or a constrictive channel flow.In addition,we incorporate the bilayer–cytoskeletal interaction in a two-component model to probe the effects of a cytoskeletal network on the gating of MS channels.
Fluid-lipid membrane interaction·Viscous flow·Mechanosensitive channels·Membrane tension
1 Introduction
Fluid–structure interactions in biophysics often involve complex coupling between chemical and mechanical processes. At the cellular level,such coupling may be achieved/facilitated by transmembrane proteins(mechanosensitive(MS) channels)that can mechanically transduce external forces on the plasma membrane to facilitate intracellular transport of chemicals:the MS channels undergo significant deformation under membrane forces above a critical magnitude and eventually open up for non-selective intracellular transport[1–3].Embedded in the plasma membrane, the interactions between the MS channels and the surrounding lipids are complex.Consequently,the mechanisms for opening and activation of MS channels depend on combinations of the detailed molecular structures[4–7],the conformational changes[8–10],and coupling with the lipid-bilayer membrane[11–14]and the cytoskeleton [15].
The MS channels ultimately detect forces at the protein–lipid interface,and their functional response was demonstrated to be governed by force from lipid(FFL)when purified bacterial mechanosensitive channels of large conductance(MscL)remained mechanosensitive after being reconstituted into bilayers[15].In the FFL paradigm the MS proteins are stretched open by membrane tension for non-selective intracellular transport of ions and macromolecules [16–20].Their gating mechanisms have been investigated by experiments[19],continuum modeling[21],and molecular dynamics(MD)simulations[22].
Patch clamp experiments of MscL reported pressure differences in the range of 24–72 mmHg(1 mmHg=133 Pa) [23]and a membrane tension of12 mN/m[24]are required to induce gating.While MD simulations estimate larger mem-brane tensions in order to open the channel(tens of mN/m) [25,26],continuum models based on the hydrophobic mismatch mechanism predict critical gating tensions ranging from 0.95 to 3.85 mN/m[27],depending on the number of carbons in the lipid chains,which influences the magnitude of hydrophobic mismatch.Recently,microfluidic pipette array experiments reported an activation tension of 4.5 mN/m in MscL-G22S(a mutant MscL with lower gating tension threshold)expressing cells[28].
The membrane tension required to open an MS channel may be generated by osmotic pressure,which ensures the survival of a cell by preventing rupture during osmotic shocks.MS channels could also be gated by flow-generated stresses.Recent experiments by Heureaux et al.[29]demonstrated that MscL expressed in mammalian cells adhered on a surface could be activated upon application of sufficiently large fluid shear stress,although the cells began to detach at that level of shear stress.Furthermore,a multi-scale model(of an MS channel and lipid-bilayer membrane system)illustrates that the fluid stress may be used to gate a single MS channel in microfluidic devices under physiologically realizable conditions[30].Two prototypical flows (a planar shear flow and flow through a narrowing constriction)were studied,and results suggest the possibility to open an MS channel by tension in the lipid-bilayer membrane going through deformation under fluid shear stress.
Analyses of flow-induced gating of MS channels can shed light on the activation of MS channels and could be applied to study mechanotransduction.In addition,microfluidics techniques have enabled the construction of artificial vesicles reconstituted with MS channels[31],and it may be possible to employ bacterial MS channels reconstituted into vesicles for drug release upon the application of fluid stresses.In this paper we further explore the effects of different flow environments on the gating of MS channels.We consider more realistic configurations where the lipid-bilayer membrane is a three-dimensional(3D)surface interacting with the surrounding fluid flow,and we also explore the implication of the bilayer-cytoskeleton interaction on the opening of MS channels.As a first step,we will employ a red blood cell (RBC)model to study the effect of the cytoskeleton on the lipid-bilayer.Although the cytoskeleton of RBCs is different from a typical mammalian cell,it will give some insights on how the cytoskeleton may influence the membrane dynamics and thus the mechanosensitive behavior of the MS channel.In addition to studying the deformation dynamics of a vesicle/cell in a planar shear flow and flow through a microfluidic channel with constriction,we study the tension in a lipid-bilayer membrane adhered on a solid substrate,a configuration motivated by recent experiments [29].
In order to establish a comparison between these three different flow environments,we characterize the strength of each background flow by the maximum shear stress within the undisturbed flow environment without the presence of a vesicle or cell.
In the following sections,we will describe the approaches we adopt to model the MS channel gating(Sect.2),the cell membrane(Sect.3.1),and the fluid-membrane interaction (Sect.3.2),before discussing the results(Sect.4)and conclusions(Sect.5).
2 Minimal models for mechanosensitive channel gating
We adopt the analytic model for gating of MS channels by Wiggins and Phillips[21],which considers the total free energy E of a cylindrical MS channel of radius R∈[Ropen,Rclosed]embedded in a lipid-bilayer membrane as

where the energy associated with membrane deformation is calculated by the membrane energy per unit length calculated in a two-dimensional(2D)setup(Gh)multiplied by the circumference of the cylindrical channel 2πR,and τ represents the membrane tension triggering channel gating.The MS channel has a minimum(Rclosed)and maximum(Ropen) radius,and it is in an open(or closed)state when the total free energy E attains its minimum value at R=Ropen(or R=Rclosed).We consider here a 2D vesicle with perimeter L and unperturbed bilayer thickness 2a.A length scale R0can be defined as the radius of the circle having the same perimeter such that L=2πR0.
To simplify the analysis we follow Ref.[21]to consider only the elastic energy contributions from the bending and thickness deformation associated with the hydrophobic mismatch



where Kbis the bending rigidity of the lipid-bilayer,Ktis the stiffness associated with membrane thickness deformation u,and s is the arclength along the bilayer membrane. Minimizing the energy functional in Eq.(2)the governing equation for u can then be obtained as The coefficients Anare determined by the constraints of hydrophobicmismatch at the MS channel:u(s=0)=u(s=2πR0)=U and the condition of zero slope at the interface[32]:us(s= 0)=us(s=2πR0)=0.Substituting the analytical solution for u into Eq.(2)we obtain the membrane energy per unit length
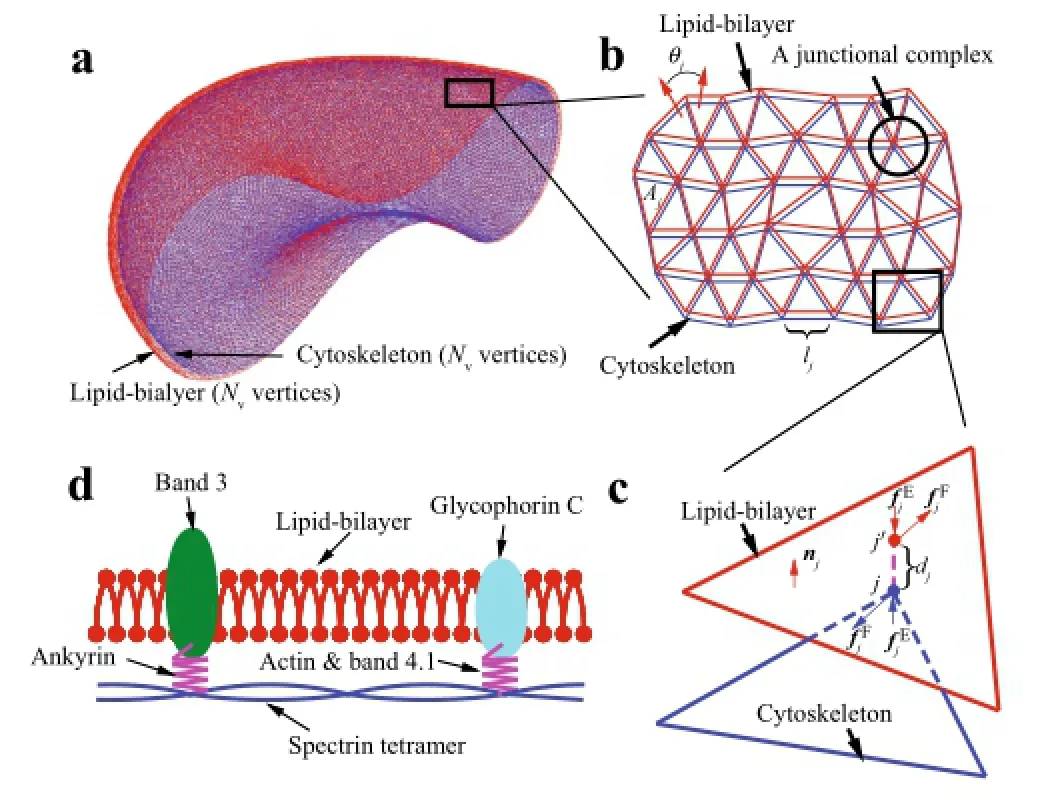
Fig.1 a Two-component model of an RBC.b Local triangular networks of the two-component model.c Normal and tangential interactions between the lipid-bilayer and the cytoskeleton. d Physical picture of the local bilayer–cytoskeletal interaction.(Adapted from Ref.[33]).For more details see Ref.[33]
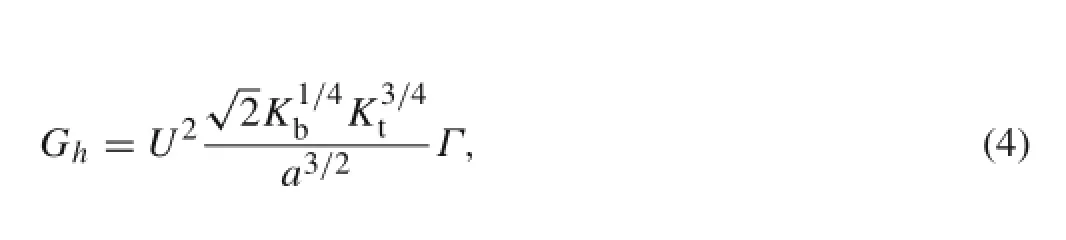
where

The critical membrane tension τcfor an MS to open can be obtained by determining the tension at which the free energies of the open and closed states are the same[27],i.e., E(R=Rclosed)=E(R=Ropen),which implies
3 Numerical simulations of vesicle and cell dynamics
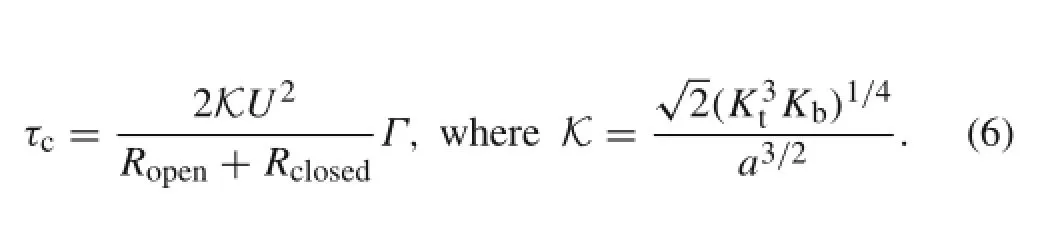
Similar to the planar case[21,27],the critical tension scales quadratically with the hydrophobic mismatch U.We first probe the effect of the vesicle size R0,which enters the critical tension only through the factor Γ(Eq.(5)),and Γ becomes approximately constant(≈1)in the Λ ≫ 1 regime.With typical lipid-bilayer properties:Kb=50kBT, Kt=60 kB/nm2,a=2 nm,and a vesicle radius of 1µm,the value of Λ≈523 is typically large.The vesicle size,therefore,does not play a significant role in the value of critical tension,which is approximately given by τc≈ 2K U2/(Ropen+Rclosed)for typical biological settings.With Rclosed=2.3 nm and Ropen=3.5 nm[27],a hydrophobic mismatch of U=0.26 nm leads to a critical tension of τc≈2.7 mN/m.Shall the number of carbons in the lipid chains is reduced to 14(phosphatidylcholine containing monosaturated chains of 14—PC 14 bilayer),the hydrophobic mismatch is reduced by half(U=0.13 nm) [27]and the critical membrane tension can be lowered by four times τc≈0.68 mN/m.
In this work we focus on using the example of using a PC 14 bilayer and adopt the critical membrane tension τc=0.68 mN/m as a benchmark for the discussion of how different flow environments can generate the required membrane tension for gating MS channels.
3.1 Modeling the cell membrane
In our simulations,the cell membrane is modeled by two different components in the two-component model,i.e.,the lipid-bilayer and the cytoskeleton,as shown in Fig.1.Each component is represented by a 2D triangular network with Nvsmoothed dissipative particle dynamics(SDPD)particles. The total elastic energy of the RBC membrane is written as

where Usis the cytoskeleton elastic energy,given by the worm-like chain(WLC)potential and a repulsive power potential as

where ljand lmare the spectrin natural length and contour length,Nsis the number of spectrins,while xj=lj/lm.p is the persistence length,kBis the Boltzmann constant,T is the temperature,kpis the power term constant.
Ubis the elastic energy of the lipid-bilayer,which is written as
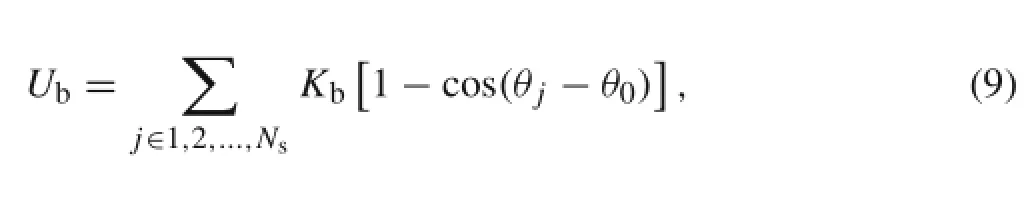

where Ntis triangle number,A0is the initial triangle area, and Ajis the current triangle area as shown in Fig.1b.is the initial volume of an RBC and Vtotis the current volume. kland kvare penalty constants.
In addition to the membrane elasticity,we also consider the viscosities of the lipid-bilayer and the cytoskeleton by adding dissipative and random forces as

where k=b,s stands for the lipid-bilayer or the cytoskeleton,respectively.are dissipative coefficients with a conditionand vijare the relative position and velocity.The membrane viscosities can be obtained as

Viscosity values of the lipid-bilayer and the cytoskeleton are chosen as 0.0125 and 0.001 pN·µm−1,respectively, which are taken from Ref.[34].
To describe the bilayer–cytoskeletal interaction,we add another term Uintas
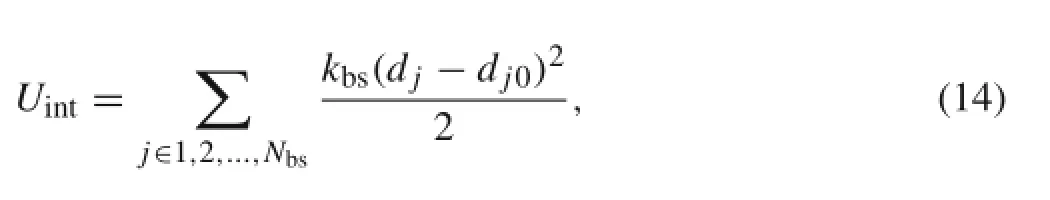
where kbsrepresents the elastic stiffness of the bonds between the bilayer and the cytoskeleton,and Nbsis the number of vertical bonds,including the bonds between the transmembrane proteins(band-3 and glycophorin C)and spectrins. We simulate the bilayer-cytoskeletal interaction by a tangential friction force and a normal viscoelastic force as shown in Fig.1c,d.djis current bond length;dj0is the initial bond length.Experiments show that dj0≈30 nm[35].We employed a master-slave penalty contact algorithm to calculate the bilayer–cytoskeletal interaction force[36].The elastic interaction force on a cytoskeletal vertex is given as

where njis the normal unit vector.We also add a vertical damping force as

where vjis the relative velocity and cbsis the damping coefficient.The bilayer–cytoskeletal viscous friction force is given as
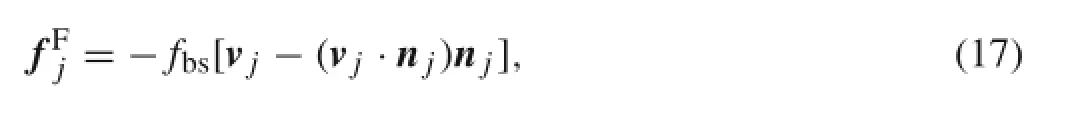
where fbsis the friction coefficient.(We choose fbs=cbsin our simulations.)
To keep the constant temperature,we add another random force as[37]


The stress on the membrane is calculated by the Virial theorem as
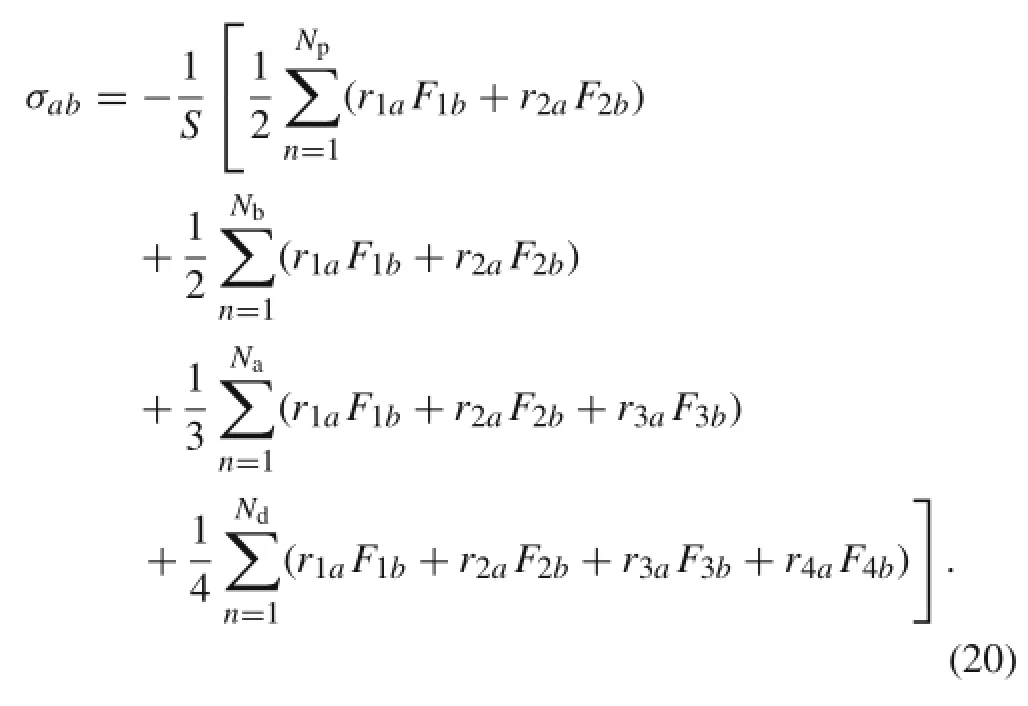
Here,the first term is a pairwise energy contribution with n loops over the Npneighbors of particle I,r1and r2are the positions of the two particles in the pairwise interaction, and F1and F2are the forces on the two particles resulting from the pairwise interaction.The second term is a bond contribution of similar form for the Nbbonds which atomI is part of.There are similar terms for the Nathree-point angle and Ndbending dihedral interactions that particle I is part of.S is the area occupied by particle I.The membrane tension is calculated as the trace of the stress tensor.

Table 1 Parameters of the lipid-bilayer

Table 2 Parameters of the cytoskeleton
The key parameters of the two-component model are provided in Tables 1 and 2.The shear modulus of the cytoskeleton is chosen to be 60 pN·µm−1,which is ten times larger than that of healthy RBCs(6 pN·µm−1),as the cells used in experiments(such as epithelial cells used in Ref.[29]) is much stiffer than RBCs.We simplify the shape of the vesicle and the cell as an ellipsoid specified by three radii.
3.2 Modeling the fluid-membrane interaction
We employ the SDPD to simulate the dynamics of vesicles and cells immersed in different flow environments.SDPD is a mesoscopic numerical method[38],which was an extension from original dissipative particle dynamics(DPD)developed to simulate fluids and polymers[39,40].It has been successfully applied to simulate red blood cells[41–43].Fluids and polymers in the SDPD simulations are represented by N SDPD particles,which interact with each other via pairwise potentials and their motions follow Newton’s second law. An SDPD particle represents a cluster of atoms,different from classical molecular dynamics.Conservative,dissipative,and random pairwise interaction forces are applied between SDPD particles i and j at positions riand rj.They are written as whereandThe strengths of dissipative and random forces are specified by constants γ and σ,respectively.The cutoff radius is defined as rc.Pi,Pj,ρi,and ρjare the pressure and density of particle i and j.Δt is the time step sizewhere d Wijis the Wiener increment. The Wiener incrementover a time step.The equation of state is given as

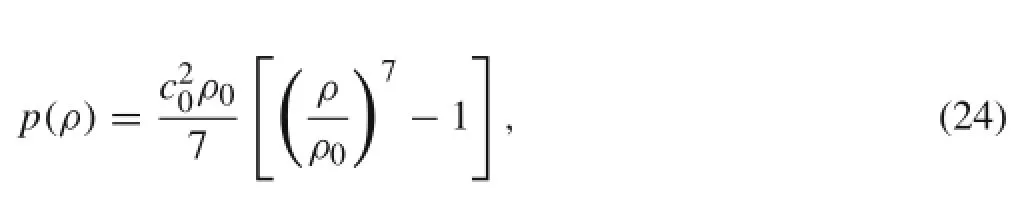
where c0is the speed of sound in water and ρ0is the initial density of water.In addition,ω(rij)is a weight function given by

The cutoff radius in this work is set to be rc=1.5846.
The interaction between the membrane particles and fluid particles are treated using DPD interactions[41].Bounce-back condition is enforced between the wall and fluid particles to achieve the no-slip condition.Bounce-back reflections of fluid particles at the membrane surface is applied to enforce the no-penetration condition[44].Furthermore,dissipative force between fluid particles and membrane particles are applied to enforce the no-slip boundary conditions at the membrane surface.
4 Results and discussion
Under a fluid flow the lipid membrane of the vesicle/cell may deform dynamically,and as a result the membrane tension may become non-uniform and time-varying.In many experiments the vesicle/cell shape deformation at equilibrium is often used as an indicator for tension in the membrane, mainly because it is difficult to measure tension directly in experiments.Motivated by recent experiments on shearing adhered cells[29],we first investigate the correlation between equilibrium deformation of adhered vesicles/cells under a shear flow(Fig.2c).Figure 3 shows the equilibrium deformation ratio of adhered vesicles and the cells under a shear flow with different initial aspect ratios of a spheroid. The radius of the adhesion area in the simulation is set to be 2µm,while in the experiments it can vary significantly[29]. The equilibrium deformation ratio is defined asλ=Dx/D0, where Dxis the maximum dimension in the x-direction of the current vesicle or cell shape and D0=2(a bc)1/3is the equivalent diameter of the original shape,where a,b,c are the three radii of the ellipsoid shape of the cell or vesicle.For the same flow shear stress,the vesicles experience larger deformation than cells,because the cells have a cytoskeleton that strengthens the effective rigidity of the cell.Furthermore, the equilibrium deformation ratio depends very weakly on the initial aspect ratios(keeping a=b=5µm and varying c=3.0,3.5,4.0µm).

Fig.2 (Color online)Simulations setups.a A cell under free shear flow.b A cell under constricted channel flow.c A cell under adhesion shear flow.Red particles represent the bilayer and blue particles represent the cytoskeleton.Purple particles represent the fluid and cyan particles represent the walls

Fig.3 The deformation ratio of the vesicle and the cell under adhesion shear flow with different aspect ratios
We then compare three different fluid environments: (1)a planar shear flow(Fig.2a),(2)channel flow through a constriction(Fig.2b)with a width of 6µm,a length of 40µm and a depth of 10µm,and(3)a shear flow applied to an adhered vesicle/cell on a solid substrate(Fig.2c).

Fig.4 Average membrane tension of a vesicle.a a=b=5µm and c=3µm.b a=b=5µm and c=3.5µm.c a=b=5µm and c=4µm
For fair comparison between these three fluid environments we use the maximum shear stress in the absence of a vesicle or RBC as a control parameter to measure the strength of each background flow.While the shear stress is uniform in case A,the maximum shear stress in the undisturbed flow occurs on the wall in cases B and C.These maximum stresses are kept the same in the three different background flows for exploring their effectiveness in inducing gating of MSchannels.We remark that for case B,a uniform pressure gradient is applied across the channel constriction with periodic boundary conditions are applied at the inlet and outlet of the computational domain in the x-direction.The computational domain size is selected to be sufficiently large so that its influence on the cell dynamics is small.

Fig.5 Maximum membrane tension of a vesicle.a a=b=5µm and c=3µm.b a=b=5µm and c=3.5µm.c a=b=5µm and c=4µm
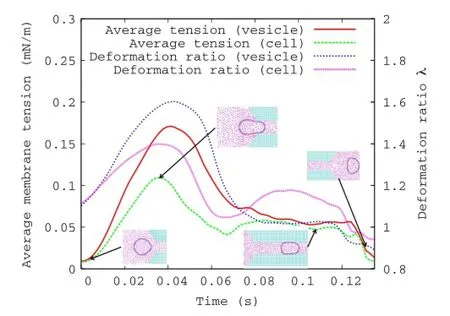
Fig.6 (Color online)Time evolution of the membrane tension and deformation ratio of a vesicle and a cell passing the constricted channel with flow shear stress of 2 Pa
We first investigate the connection between shape deformation and the development of membrane tension under the three different flow conditions.Figure 4 shows the average membrane tension(averaged over the membrane area)versus applied shear stress for vesicles with three different aspect ratios.The membrane tension in the adhesion shear case increases much faster with the applied shear stress than the other two cases,and the case of constricted channel flow observes the slowest increase in membrane tension.With the three different aspect ratios experimented,we demonstrate the weak dependence of the results on the aspect ratio (Fig.4a–c).
The average membrane tension in all three cases is below the benchmark critical membrane tension(τc=0.68 mN/m) for opening an MS channel.The maximum membrane tension follows the same trends as the average membrane stress as shown in Fig.5,and membrane tension beyond the critical membrane tensionτccan be reached for sufficiently large applied shear stress.For example,the membrane tension of a vesicle in the adhesion shear case and the free shear case can reach a maximum value of 1.5 mN/m,upon an applied shear stress of 1.5 and 3 Pa,respectively.
Even in the slowly increasing constricted channel flow case,the membrane tension reach 0.9 mN/m under the application a shear stress of 3 Pa.In our simulation setup for the constriction channel(based on experimental setup in Ref.[28]),the size of the constriction is chosen so the vesicle/cell can flow through the constriction instead of blocking the channel as in micropipette experiments.We show in Fig.6 the evolution of average tension(red solid line)and deformation ratio(blue dotted line)of the vesicle as it approaches, passes through,and leaves the channel constriction.There is a high correlation between deformation and membrane tension,and both of them attain their maximum values as the vesicle first enters the channel constriction.Inside the constriction,the membrane tension relaxes as the vesicledeformation decreases,and the membrane tension sharply drops to almost zero as the vesicle exits the channel constriction.This example also demonstrates that the membrane tension varies dynamically in both space and time,and special care must be taken when inferring membrane tension from membrane shape.
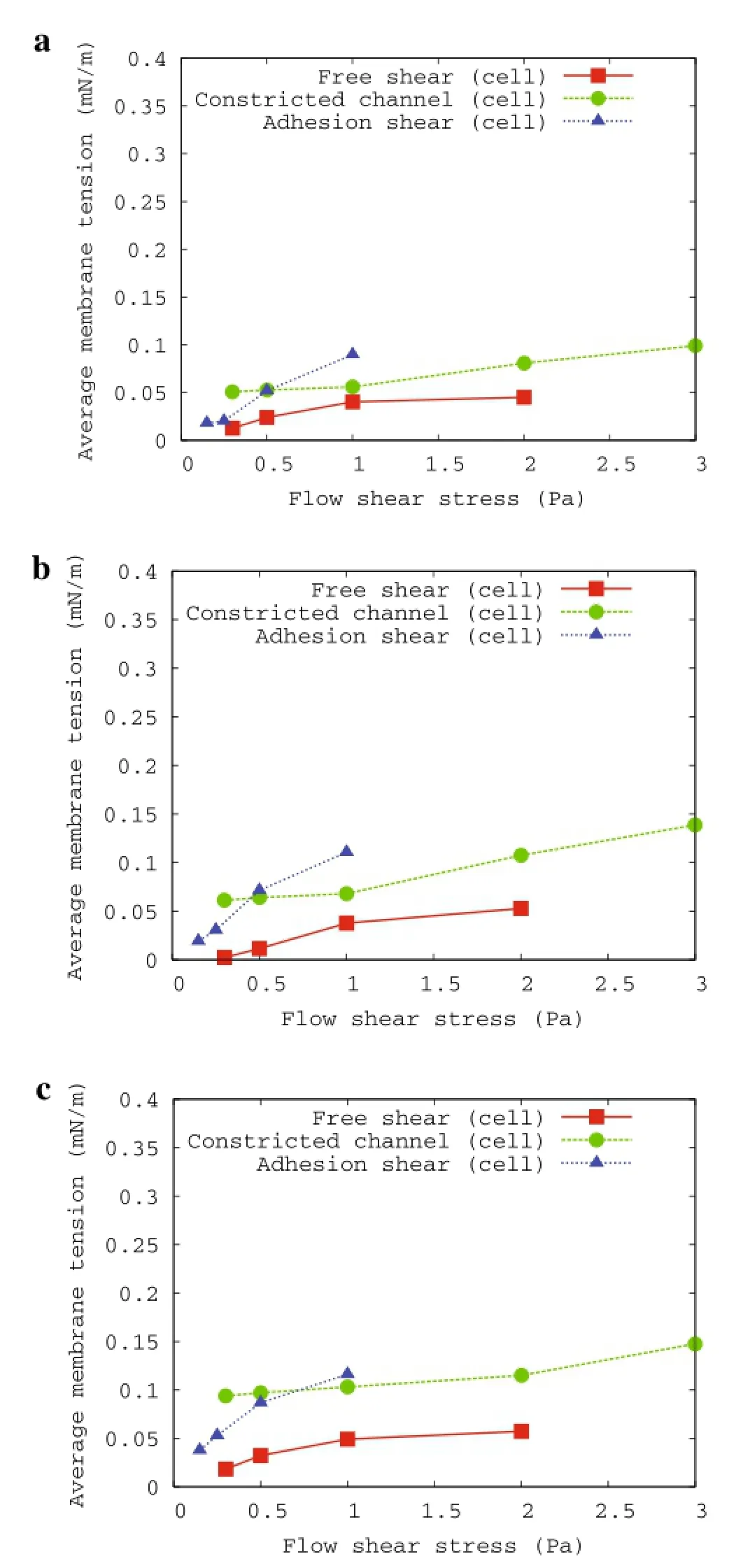
Fig.7 Average membrane tension of a cell.a a=b=5µm and c=3µm.b a=b=5µm and c=3.5µm.c a=b=5µm and c=4µm

Fig.8 Maximum membrane tension of a cell.a a=b=5µm and c=3µm.b a=b=5µm and c=3.5µm.c a=b=5µm and c=4µm
Furthermore,we investigate the effect of the cytoskeletal network(a cell)on the dynamics of membrane tension for the same flow conditions in Figs.7 and 8.Under the same flow shear stress,both the average and maximum membrane tensions in cells are smaller than the corresponding cases in vesicles,especially for high shear stress.The evolution of deformation ratio and average membrane tension for a cellthrough a channel constriction is shown in Fig.6.The general trends of smaller deformation(violent dotted line)and lower membrane tension(green dotted line)compared with the case of a vesicle still apply.

Fig.9 Effect of the flow shear stress on the percentage of area where the MS channels are open for vesicles under three flow conditions. Insets membrane tension distribution in the A free shear,B constricted channel,and C adhesion shear cases.Areas with membrane tension greater than the critical membrane tension τcare highlighted

Fig.10 a Membrane tension distribution of a cell under free shear flow.b Normal cytoskeleton stress applied on the lipid-bilayer under free shear flow.c Membrane tension distribution of a cell under adhesion shear flow.d Normal cytoskeleton stress applied on the lipid-bilayer under adhesion shear flow.e Membrane tension distribution of a cell under constricted channel flow.f Normal cytoskeleton stress applied on the lipid-bilayer under constricted channel flow
Finally,we represent our results in terms of the percentage of area where the membrane tension exceeds the critical membrane τc=0.68 mN/m,in which case the MS channel can open,under the three different flow environments as a function of the applied shear stress(Fig.9).We can see that the adhesion shear case is the most effective in inducing gating over a large portion of area of the vesicle,followed by the channel flow through a constriction.For illustration,typical membrane tension distributions upon an applied shear stress of 3 Pa are shown on the vesicle surfaces for the three flow scenarios,and we have highlighted the regions where MS channels can open in the three different flows(Fig.9 insets A–C).At this level of shear stress,over 20%area of the adhered vesicle attains membrane tension greater than the critical membrane tension(Fig.9 insets C).For the channel constriction case(Fig.9 insets B),the region with tension greater than the critical value occurs at the front end of the vesicle passing through the channel constriction,similar to the findings in Ref.[30].The corresponding membrane tension distributions for a cell under the three flow conditions are shown in Fig.10a,c,e.Since the overall deformation and membrane tension are lower than the corresponding vesicle cases,none of the three flow environments can attain sufficiently high membrane tension to induce gating,given the benchmark critical membrane tension adopted in this work.As a remark,it has been recently suggested that normal forces exerted through the cytoskeletal network on the bilayer membrane may also contribute to the gating of MS channels.With our two-component cell model,information about the normal force can be readily extracted(Fig.10b,d, f),which may be useful for modeling the proposed gating mechanism.
5 Conclusions
Based on the FFL paradigm for the functioning of MS channels,in this work we investigate which configuration would be most effective to induce large membrane tension for gating an MS channel open by external fluid shear stress. Using SDPD,we simulate the deformation of a lipid-bilayer membrane(with or without coupling to a cytoskeleton)and investigate how membrane tension varies under fluid flow conditions that are motivated by physiological configurations and microfluidic experimental setups.
For both vesicle and cell,the lipid-bilayer membrane deforms when experiencing a shear stress from the surrounding fluid flow.Simulations results suggest that shearing of adhered vesicles/cells is the most effective in inducing large membrane tension for gating MS channels open.In addition,we visualize the spatial distribution of membrane tension and locate possible locations for MS channel to experience sufficiently large force to be gated open.We alsofind that membrane deformation is not always related to membrane tension in a straightforward fashion,especially in the dynamical setup such as the constriction channel flow.
Our results further suggest that a cytoskeleton tends to reduce the membrane deformation and tension,and thus make it difficult for MS channels to open solely from the membrane tension.However,we consider here only the hydrophobic mismatch gating mechanism and other possible gating mechanisms have been suggested[45,46], which could exploit the interaction between the bilayer and cytoskeleton,for instance,the normal forces exerted by the cytoskeletal network on the bilayer,potentially to lower the critical membrane tension for MS channels to open.Our two-component cell model simulations results reveal that the magnitude of normal stress(σ33)between the bilayer and cytoskeleton are non-negligible,which suggests incorporating other plausible gating mechanisms in the theoretical model.
References
1.Kung,C.,Martinac,B.,Sukharev,S.:Mechanosensitive channels in microbes.Annu.Rev.Microbiol.64,313–329(2010)
2.Martinac,B.,Kloda,A.:Mechanosensory transduction.Compr. Biophys.6,108–141(2012)
3.Sackin,H.:Mechanosensitive channels.Annu.Rev.Physiol.57, 333–353(1995)
4.Betanzos,M.,Chiang,C.-S.,Guy,H.R.,et al.:A large iris-like expansion of a mechanosensitive channel protein induced by membrane tension.Nat.Struct.Biol.9,704(2002)
5.Blount,P.,Sukharev,S.I.,Schroeder,M.J.,et al.:Single residue substitutions that change the gating properties of a mechanosensitive channel in Escherichia coli.Proc.Natl.Acad.Sci.USA 93, 11652–11657(1996)
6.Sukhareva,S.,Sachs,F.:Molecular force transduction by ion channels—diversity and unifying principles.J.Cell Sci.125,3075 (2012)
7.Sukharev,S.,Durell,S.R.,Guy,H.R.:Structural models of the mscl gating mechanism.Biophys.J.81,917–936(2001)
8.Kong,Y.,Shen,Y.,Warth,T.E.,et al.:Conformational pathways in the gating of Escherichia coli mechanosensitive channel.Proc. Natl.Acad.Sci.USA 99,5999–6004(2002)
9.Ollila,O.H.S.,Risselada,H.J.,Louhivuori,M.,et al.:3d pressure field in lipid membranes and membrane-protein complexes.Phys. Rev.Lett.102,078101(2009)
10.Yoshimura,K.,Usukura,J.,Sokabe,M.:Gating-associated conformational changes in the mechanosensitive channel mscl.Proc. Natl.Acad.Sci.USA 105,4033–4038(2008)
11.Mukherjee,N.,Jose,M.D.,Brikner,J.P.,et al.:The activation mode of the mechanosensitive ion channel,mscl,by lysophosphatidylcholine differs from tension-induced gating.FASEB 28, 4292–4302(2014)
12.Phillips,R.,Ursell,T.,Wiggins,P.,et al.:Emerging roles for lipids in shaping membrane-protein function.Nature 459,379(2009)
13.Vanegas,J.M.,Arroyo,M.:Force transduction an lipid binding in mscl:a continuum-molecular approach.PLOS ONE 9,0113947 (2014)
14.Sukharev,S.,Akitake,B.,Anishkin,A.:The bacterial mechanosensitive channel mscs:emerging principles of gating and modulation. Curr.Top.Membr.58,235–267(2007)
15.Kung,C.:A possible unifying principle for mechanosensation. Nature 436,647(2005)
16.Teng,J.,Loukin,S.,Anishkin,A.,etal.:The force-from-lipid(FFL) principle of mechanosensitivity,at large and in elements.Pflugers Arch.Eur.J.Physiol.467,27–37(2015)
17.Belyy,V.,Anishkin,A.,Kamaraju,K.,et al.:The tensiontransmitting‘clutch’in the mechansensitive channel mscs.Nat. Struct.Mol.Biol.17,451–459(2010)
18.Hamill,O.P.,Martinac,B.:Molecular basis of mechanotransduction in living cells.Physiol.Rev.81,685(2001)
19.Martinac,B.,Buechner,M.,Delcour,A.H.,et al.:Pressuresensitive ion channel in Escherichia coli.Proc.Natl.Acad.Sci. USA 84,2297–2301(1987)
20.Sachs,F.:Mechanical transduction by membrane ion channels:a mini review.Mol.Cell.Biochem.104,57–60(1991)
21.Wiggins,P.,Phillips,R.:Analytic models for mechanotransduction:gating a mechanosensitive channel.Proc.Natl.Acad.Sci. USA 101,4071–4076(2004)
22.Jeon,J.,Voth,G.A.:Gating of the mechanosensitive channel protein mscl:the interplay of membrane and protein.Biophys.J.94, 3497–3511(2008)
23.Perozo,E.,Kloda,A.,Cortes,D.M.,et al.:Physical principles underlying the transduction of bilayer deformation forces during mechanosensitive channel gating.Nat.Struct.Mol.Biol.9,696–703(2002)
24.Sukharev,S.I.,Sigurdson,W.J.,Kung,C.,et al.:Energetic and spatial parameters for gating of the bacterial large conductance mechanosensitive channel,mscl.J.Gen.Physiol.113,525–539 (1999)
25.Louhivuori,M.,Risselada,H.J.,van der Giessen,E.,et al.:Release of content through mechano-sensitive gates in pressurized liposomes.Proc.Natl.Acad.Sci.USA 107,19856–19860(2010). doi:10.1073/pnas.1001316107
26.Deplazes,E.,Louhivuori,M.,Jayatilaka,D.,etal.:Structural investigation of mscl gating using experimental data and coarse grained md simulations.PLoS Comput.Biol.8,e1002683(2012)
27.Phillips,R.,Kondev,J.,Theriot,J.:Physical Biology of the Cell. Garland Science,Taylor and Francis Group,New York(2012)
28.Lee,L.M.,Liu,A.P.:A microfluidic pipette array for mechanophenotyping of cancer cells and mechanical gating of mechanosensitive channels.Lab Chip 15,264–273(2015)
29.Heureaux,J.,Chen,D.,Murray,V.L.,et al.:Activation of a bacterial mechanosensitive channel in mammalian cells by cytoskeletal stress.Cell.Mol.Bioeng.7,307–319(2014)
30.Pak,O.S.,Young,Y.-N.,Marple,G.R.,et al.:Gating of a mechanosensitive channel due to cellular flows.Proc.Natl.Acad. Sci.USA 112,9822–9827(2015)
31.Ho,K.K.Y.,Murray,V.L.,Liu,A.P.:Engineering artificial cells by combining HeLa-based cell free expression and ultrathin double emulsion template.Methods Cell Biol.128,303–318(2015)
32.Huang,H.W.:Deformation free energy of bilayer membrane and its effect on gramicidin channel lifetime.Biophys.J.50,1061–1070 (1986)
33.Peng,Z.,Li,X.,Pivkin,I.V.,et al.:Lipid bilayer and cytoskeletal interactions in a red blood cell.Proc.Natl.Acad.Sci.USA 110, 13356–13361(2013)
34.Berk,D.A.,Hochmuth,R.M.,Waugh,R.E.:Viscoelastic properties and rheology,red blood cell membranes.In:Agre,P.,Parker,J.C. (eds.)Red Blood Cell Membranes,Marcel Dekker,New York,445–446(1989)
35.Heinrich,V.,Ritchie,K.,Mohandas,N.,et al.:Elastic thickness compressibilty of the red cell membrane.Biophys.J.81,1452–1463(2001)
36.Malone,J.G.,Johnson,N.L.:A parallel finite-element contact/impact algorithm for nonlinear explicit transient analysis 1. The search algorithm and contact mechanics.Int.J.Numer.Methods Eng.37,559–590(1994)
37.Espanol,P.:Fluid particle model.Phys.Rev.E 57,2930–2948 (1998)
38.Espanol,P.,Revenga,M.:Smoothed dissipative particle dynamics. Phys.Rev.E 67,026705(2003)
39.Hoogerbrugge,P.J.,Koelman,J.M.V.A.:Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys.Lett.19,155–160(1992)
40.Groot,R.D.,Warren,P.B.:Dissipative particle dynamics:bridging the gap between atomistic and mesoscopic simulation.J.Chem. Phys.107,4423–4435(1997)
41.Fedosov,D.A.,Peltomaki,M.,Gompper,G.:Deformation and dynamics of red blood cells in flow through cylindrical microchannels.Soft Matter 10,4258–4267(2014)
42.Muller,K.,Fedosov,D.A.,Gompper,G.:Smoothed dissipative particle dynamics with angular momentum conservation.J.Comput. Phys.281,301–315(2015)
43.Katanov,D.,Gompper,G.,Fedosov,D.A.:Microvascular blood flow resistance.Microvasc.Res.99,57–66(2015)
44.Fedosov,D.A.,Caswell,B.,Karniadakis,G.E.:A multiscale red blood cell model with accurate mechanics,rheology,and dynamics. Biophys.J.98,2215–2225(2010)
45.Ge,J.,Li,W.,Zhao,Q.,et al.:Architecture of the mammalian mechanosensitive piezol channel.Nature 527,64–69(2015)
46.Sabass,B.,Stone,H.A.:Role of the membrane for mechanosensing by tethered channels.Phys.Rev.Lett.116,258101(2016)
DOI 10.1007/s10409-016-0606-y
✉ Zhangli Peng zpeng3@nd.edu
1Department of Aerospace and Mechanical Engineering, University of Notre Dame,Notre Dame,IN 46556,USA
2Department of Mechanical Engineering,Santa Clara University,Santa Clara,CA 95053,USA
3Department of Mechanical Engineering,University of Michigan,Ann Arbor,MI 48109,USA
4Department of Mathematical Sciences,New Jersey Institute of Technology,Newark,NJ 07102,USA
1 February 2016/Revised:21 June 2016/Accepted:14 July 2016/Published online:14 October 2016
- Acta Mechanica Sinica的其它文章
- Plaque components affect wall stress in stented human carotid artery:A numerical study
- Time-delay identification for vibration systems with multiple feedback
- Thermoelastic analysis of multiple defects with the extended finite element method
- Static and dynamic responses of a microcantilever with a T-shaped tip mass to an electrostatic actuation
- Closed-form solutions for free vibration of rectangular FGM thin plates resting on elastic foundation
- A semi-analytical approach for calculating the equilibrium structure and radial breathing mode frequency of single-walled carbon nanotubes

