Closed-form solutions for free vibration of rectangular FGM thin plates resting on elastic foundation

T.F.Xu·Y.F.Xing

Closed-form solutions for free vibration of rectangular FGM thin plates resting on elastic foundation

T.F.Xu1,2·Y.F.Xing1

©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016

This article presents closed-form solutions for the frequency analysis of rectangular functionally graded material(FGM)thin plates subjected to initially in-plane loads and with an elastic foundation.Based on classical thin plate theory,the governing differential equations are derived using Hamilton’s principle.A neutral surface is used to eliminate stretching–bending coupling in FGM plates on the basis of the assumption of constant Poisson’s ratio.The resulting governing equation of FGM thin plates has the same form as homogeneous thin plates.The separation-of-variables method is adopted to obtain solutions for the free vibration problems of rectangular FGM thin plates with separable boundary conditions,including,for example,clamped plates.The obtained normal modes and frequencies are in elegant closed forms,and present formulations and solutions are validated by comparing present results with those in the literature and finite element method results obtained by the authors.A parameter study reveals the effects of the power law index n and aspect ratio a/b on frequencies.

Functionally graded material·Free vibration· Rectangular plate·Close form solutions·Neutral surface

DOI 10.1007/s10409-016-0600-4

1 Introduction

Functionally graded material(FGM)is inhomogeneous composite materials that has received considerable attention inmany engineering applications.FGM was proposed in 1984 [1,2]as thermal barrier materials.FGM show a continuous variation in its material properties along a certain direction and is now being extensively used in aircraft,spacecraft,and various other industries because the strength and stiffness of FGM give it flexibility in design.

The vibration problem of isotropic and composite rectangular plates continues to be of considerable research interest. As for isotropic and orthotropic rectangular thin plates,many studies are available in the literature,for example,by Xing and coworkers[3–5]have obtained closed-form solutions for rectangular thin plates with two adjacent clamped edges for the first time.As for rectangular FGM thin plates,most of the studies were published in the last15 years;representative ones related to the present study are reviewed in what follows.

Studies based on the classical thin plate theory(CPT)are reviewed first.Yang and Shen[6]dealt with the dynamic response of initially stressed FGM thin plates by the differential quadrature(DQ)method and the Galerkin procedure. Abrate[7,8]used the extensive results available in the literature to show that the natural frequencies,in-plane buckling loads,critical temperatures,and deflections of FGM plates are proportional to those of homogeneous plates;it was also shown that by a proper choice of reference surface,coupling between in-plane and bending deformations can be eliminated.Zhang and Zhou[9]defined a physical neutral(PN) surface and showed that it is simply the reference surface by which stretching–bending coupling can be eliminated.Yin et al.[10]carried out a free vibration analysis of FGM thin plates using a rational B-spline and PN surface.Li et al.[11] derived scaling factors between solutions of bending,buckling,and free vibrations of isotropic FGM thin plates and those of the corresponding isotropic homogeneous plates and stated the conditions for the existence of a PN surface.

As for studies based on different shear deformation theories,Thai and Uy[12]obtained closed-form solutions for a buckling analysis of an FGM plate with two opposite edges simply supported using refined plate theory.Reddy et al.[13] used first-order shear deformation theory(FSDT)for bending and stretching analyses of axisymmetric FGM annular and circular plates and expressed the solutions in terms of the corresponding quantities of isotropic plate based on the CPT.Hosseini-Hashemi et al.[14]presented exact solutions for the free vibration of rectangular FGM plates with two opposite edges simply supported based on the FSDT.Reddy [15]presented both a theoretical formulation and finite-element model based on third-order shear deformation theory (TSDT).Yang and Shen[16]used DQ technique,Galerkin approach,and modal superposition method to determine the free and forced vibration behavior of initially stressed FGM plates in a thermal environment based on the TSDT.Kim [17]developed a theoretical method using a Rayleigh–Ritz procedure to investigate the vibration characteristics of initially stressed FGM plates via third-order shear deformation plate theory,where two types of thermal condition were considered.

Recently,Swaminathan et al.[18]presented a review of the various methods used to study the static,dynamic,and stability behavior of FGM plates.Thai and Kim[19]reviewed existing theories of the modeling and analysis of FGM plates and shells,with the main emphasis on equivalent-single-layer theory models,such as CPT,TSDT,and others.Sayyad and Ghugal[20]reviewed the application of various methods to the vibration analysis of laminated composite and sandwich plates.

From these reviews one can see that the vibration behavior of FGM thin plates has been investigated,while but most of the papers used numerical methods.In addition,closed-form solutions for the free vibration of rectangular FGM plates are only available for plates with parallel,simply supported sides,whether for CPT or FSDT.Thai and Uy[12] and Hosseini-Hashemi et al.[14]presented closed-form solutions for the free vibrations of rectangular FGM plates using different shear deformation theories.Li et al.[11]investigated the vibration solutions of FGM plates based on CPT, but no explicit analytical solutions were presented.Furthermore,there is no closed-form solution for FGM plates with two adjacent clamped edges to date.

In this context,one of the aims of this paper is to eliminate the stretching–bending coupling of FGM thin plates by taking a the neutral surface as the reference surface;the other aim is to obtain closed-form normal modes and frequencies of rectangular FGM thin plates with separable boundary conditions using a separation-of-variables approach.Comprehensive comparisons and numerical results in dimensionless form validate the present work and reveal the effects of power law index n and aspect ratio a/b on frequency.The highlight of this paper is the solution method by which closed-form normal modes and frequencies are obtained for rectangular FGM thin plates with separable boundary conditions.

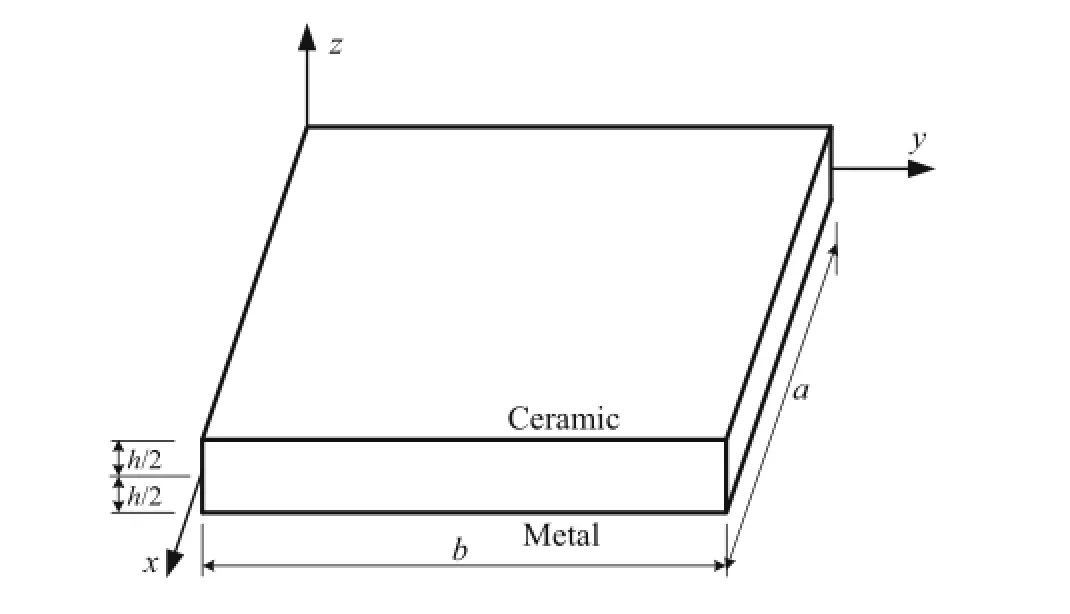
Fig.1 A rectangular FGM plate and coordinates

2 Theoretical formulations

Consider an FGM plate of length a,width b,and thickness h that is made from a mixture of ceramics and metals(Fig.1). The FGM is assumed to vary from the ceramic-rich top surface(z=h/2)to the metal-rich bottom surface(z=−h/2). The effective Young’s modulus E,mass density ρ,and Poisson’s ratio ν of the FGM plate can be written in a power law as[21]

in which the variables with subscripts t and b denote the properties of the top and bottom surfaces of the plate,respectively, and n is the power law index.The volume fraction index n indicates the material variation profile through the plate thickness.The value n=0 represents a ceramic plate.

The present study is based on CPT;taking the geometrical midplane of the plate as the origin plane of the z coordinate results in the following displacement field:

where u0and v0are the in-plane displacements of the geometrical midplane of the plate along the x-and y-directions,respectively,and w is the transverse displacement.The strains associated with the displacement field in Eq.(2)are given by

where

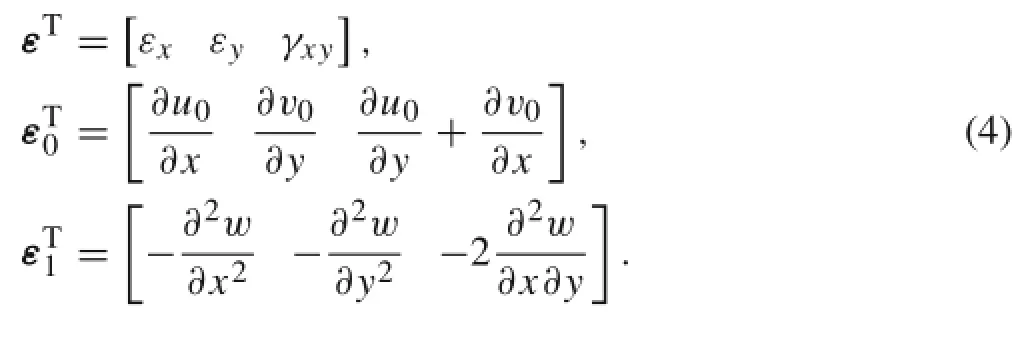
The stresses can be determined from the constitutive relations of the FGM plate as

where

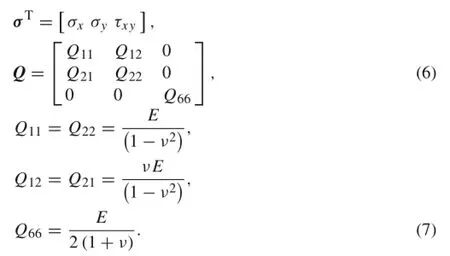
The in-plane forces and transverse moments can be written as

where

Substituting Eq.(5)into Eq.(8),one obtains

where A,B,and D are the plate extensional,coupling,and bending stiffness,respectively,defined by

The strain energy of the thin plate can be written as

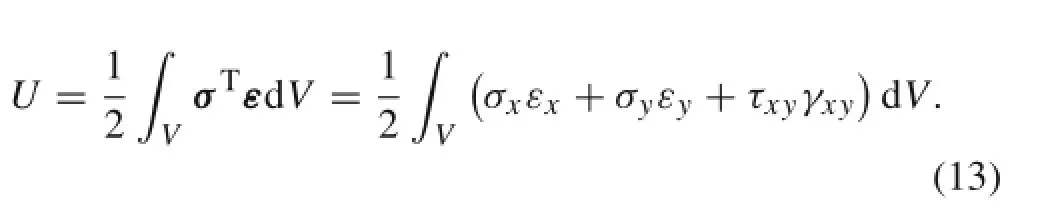
where

Substituting Eqs.(3)and(5)into Eq.(13)and integrating through the thickness of the plate,the strain energy has the form

The work done by applied external forces is

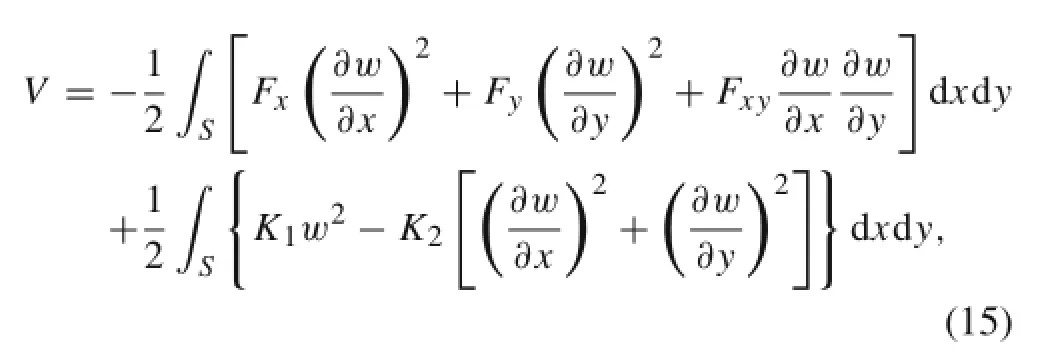
where Fx,Fy,Fxyare the in-plane distributed forces,and K1and K2are the Winkler and Pasternak foundation stiffnesses, respectively.

The kinetic energy of the plate is

where

Note that I1=0 for isotropic and homogeneous materials. In this work,the dynamic equations are derived using Hamilton’s principle?t0δ(U+V−T)d t=0 as

where the differential operators L and the derived natural boundary conditions are presented in Appendix 2.From Eq.(18)we see that the in-plane stretching and bending couple together because the geometrical midplane is chosen as the reference surface above in which there is in-plane stretching due to the materials’being asymmetrical with respect to the midplane.However,the coupling of the in-plane stretching and bending can be eliminated easily by choosing another surface as a reference surface in which there are no in-plane displacements,and this surface can be called the neutral surface.

Henceforth,we choose the neutral surface as the reference surface rather than the geometrical midplane,and,in conjunction with the CPT assumptions,the in-plane displacements of the midplane can be expressed in terms of the slopes of deflection as follows

where z0is the distance between the neutral surface and the midplane,and z0is to be determined.One finds that the in-plane displacements of the neutral surface equal zero by inserting Eqs.(19)into Eq.(2)and letting z=z0;in addition, one also finds that all in-plane stresses equal zero(refer to Eqs.(3)–(5)).Note that the in-plane stretching and bending have been uncoupled owing to the introduction of Eq.(19), although z0has not yet been determined.A method to determine z0is given below.

Using Eq.(19)we can obtain the in-plane internal forces of the neutral surface:

As shown above,the variables u=v=0,and σ=0 on the neutral surface;then N=0,which requires all elements of the coefficient matrix in Eq.(20)to be zeros since the strains ε0in the midplane are not zeros.Therefore,one has

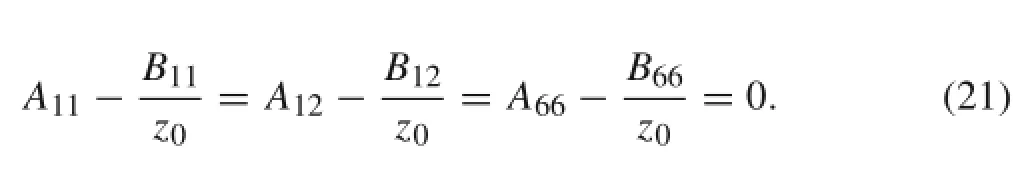
These relations require that the Poisson’s ratio ν be a constant.Hence,we have

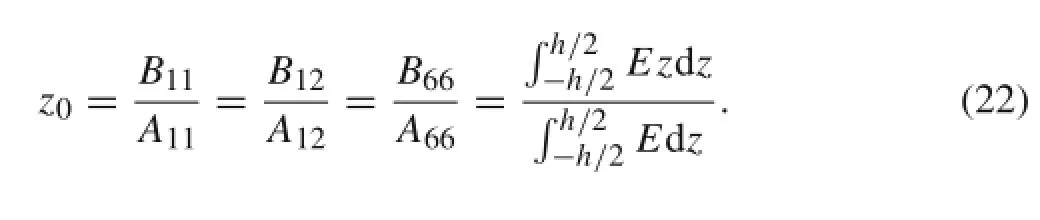
This is the same as in Ref.[9],where the term physical neutral surface was used.Another point is that,in general,the mass neutral surface I1/I0/=z0,and so the in-plane inertial forces must not be zeros in the transverse vibration of the FGM plate;refer to Eq.(18a)and(18b).But in the present study, there is much less in-plane inertia than transverse inertia since the thin plate problem is discussed on the basis of CPT,so that problem is ignored here.

By substituting Eq.(19)into Eq.(18c),one finds that the last two terms of Eq.(18c)represent the rational inertia of a cross section of the thin plate,which can be ignored in comparisons with transverse translational inertia.The principal vibration is harmonic;then

Inserting Eq.(19),Eq.(22),and Eq.(23)into Eq.(18c)and neglecting Eq.(18c)’s last two terms,we have

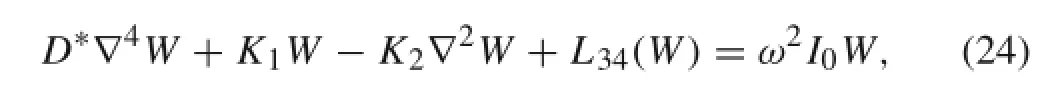
where

Equation(24)shows that the characteristic differential equation of FGM thin plates has the same mathematical form as that of homogeneous thin plates based on CPT;hence, FGM thin plates behave like homogeneous thin plates or can be equivalent to homogeneous thin plates.Additionally,the boundary conditions of FGM thin plates have the same forms as those of homogeneous thin plates,as shown in Table 1.

3 Closed-form solution

In this work a separation-of-variables solution of Eq.(24)is assumed,

Table 1 Boundary conditions of FGM thin plates

whereφ andψ are respectively the x-and y-directions mode functions or eigenfunctions,and we assume they are

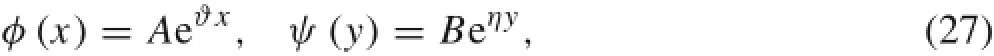
where the variables ϑ and η are the eigenvalues of the x-and y-directions,respectively.In the classical separation-of-variables method,either ϑ or η and its corresponding eigenfunction are given or assumed for the pair of opposites simply supported or guided edges;then the plate problems resemble beamlike problems.In contrast,both these spatial eigenvalues and frequencies are unknown and solved simultaneously in the present work,and the coefficients of W and the eigenvalue equations can be determined via the boundary conditions of the four edges.Moreover,the relationships among the two spatial eigenvalues and the temporal eigenvalue are solved by substituting Eq.(26)into Eq.(24),

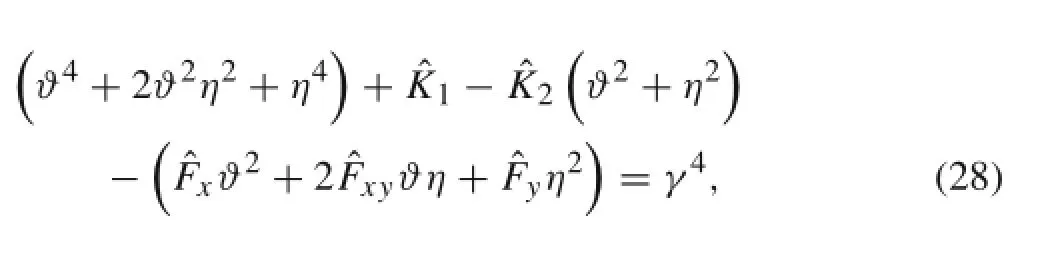
where

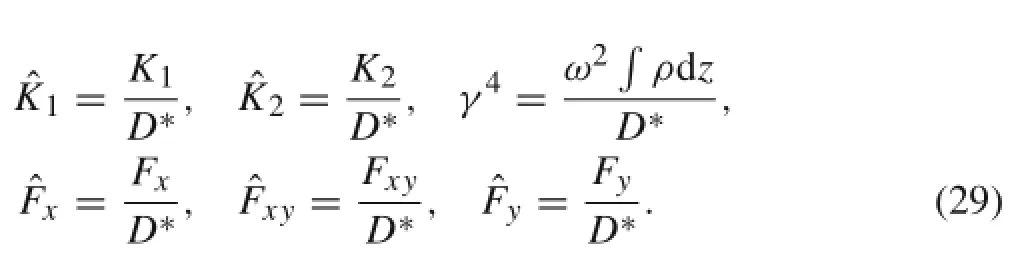
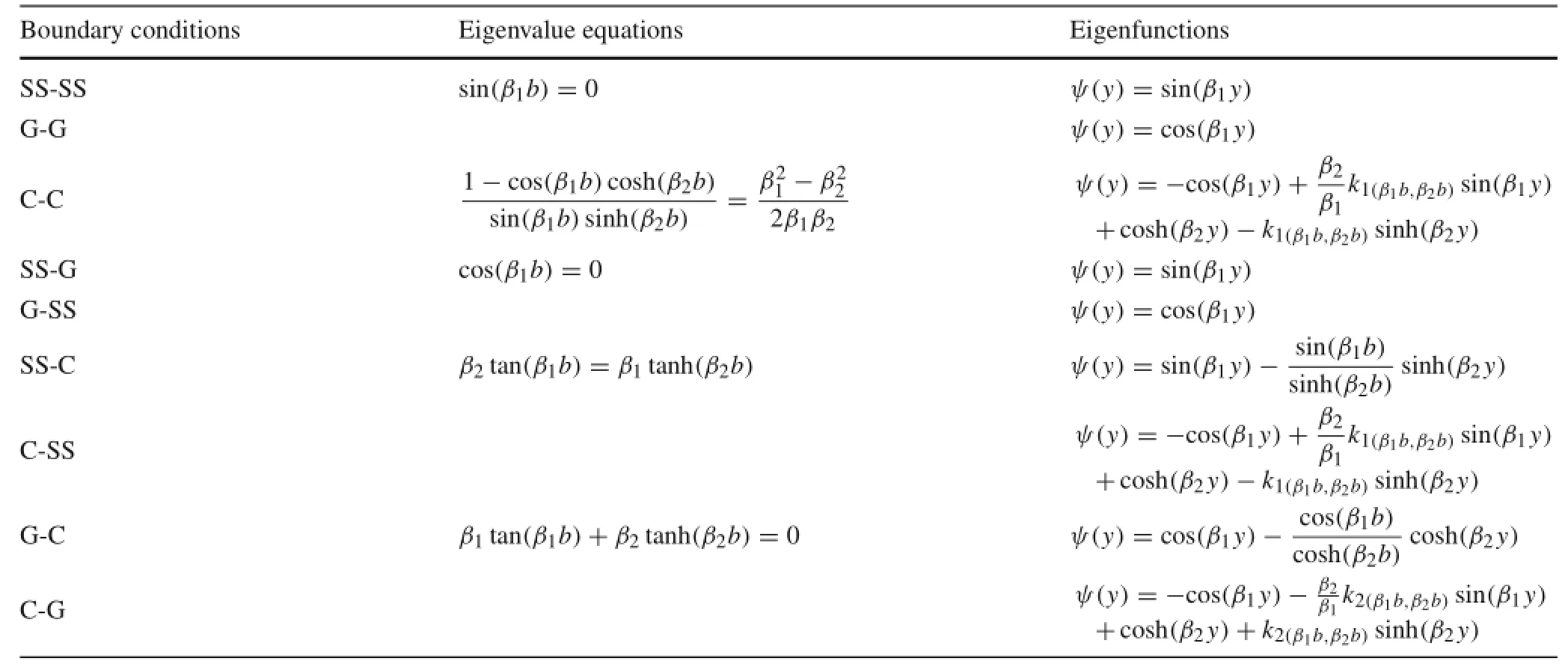
Table 2 y-direction eigenvalues and eigenfunctions

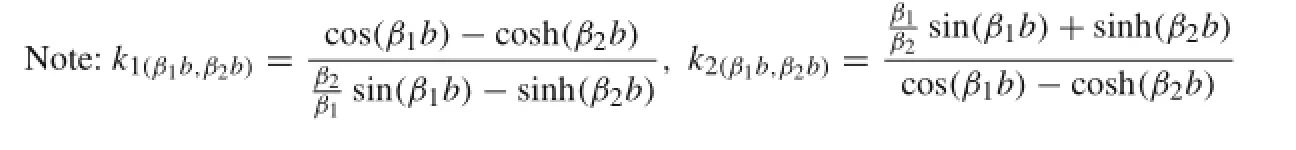
Henceforth,the in-plane distributed force Fxyis ignored hereinafter.Then Eq.(28)becomes

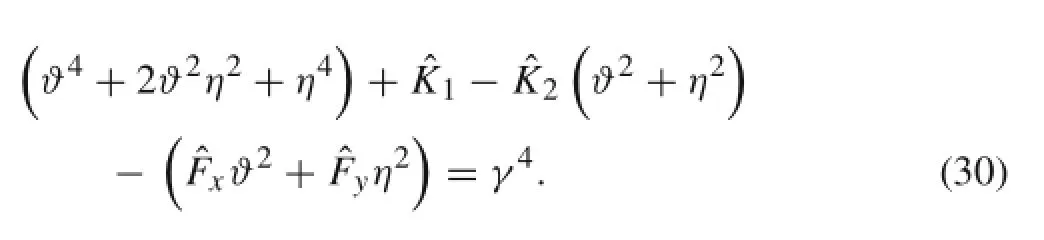
It can be seen from Eq.(30)that the eigenvalues ϑ and η can be real,imaginary,or conjugate,and their different combinations give differential frequencies.Givenϑ,ηcan be expressed by ϑ and γ;similarly,given η,ϑ can be expressed by η and γ;therefore,we have

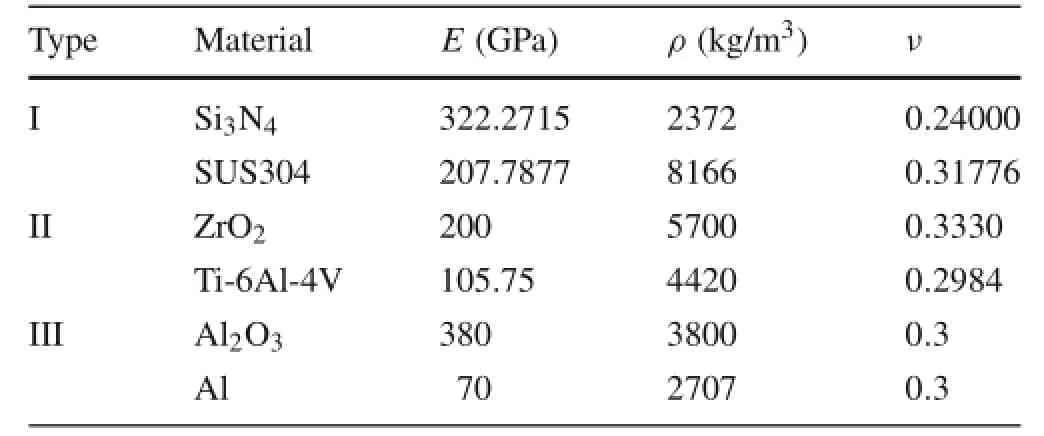
Table 3 Material properties(at T=300 K)

where i2=−1,and

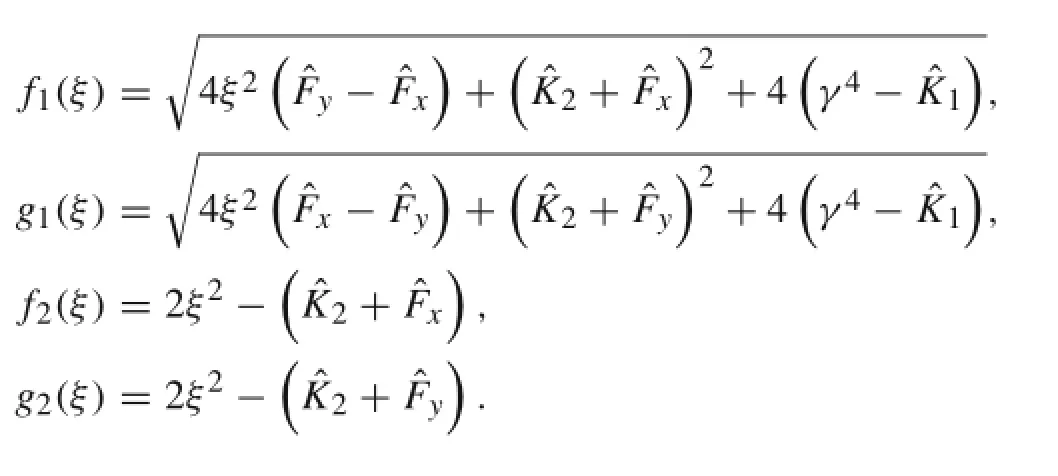
Substituting η=iβ1into Eq.(31)and ϑ=iα1into Eq.(32) yields

Fig.2 Boundary conditions of plates with two adjacent clamped edges and combinations of C,SS,and G conditions for remaining edges

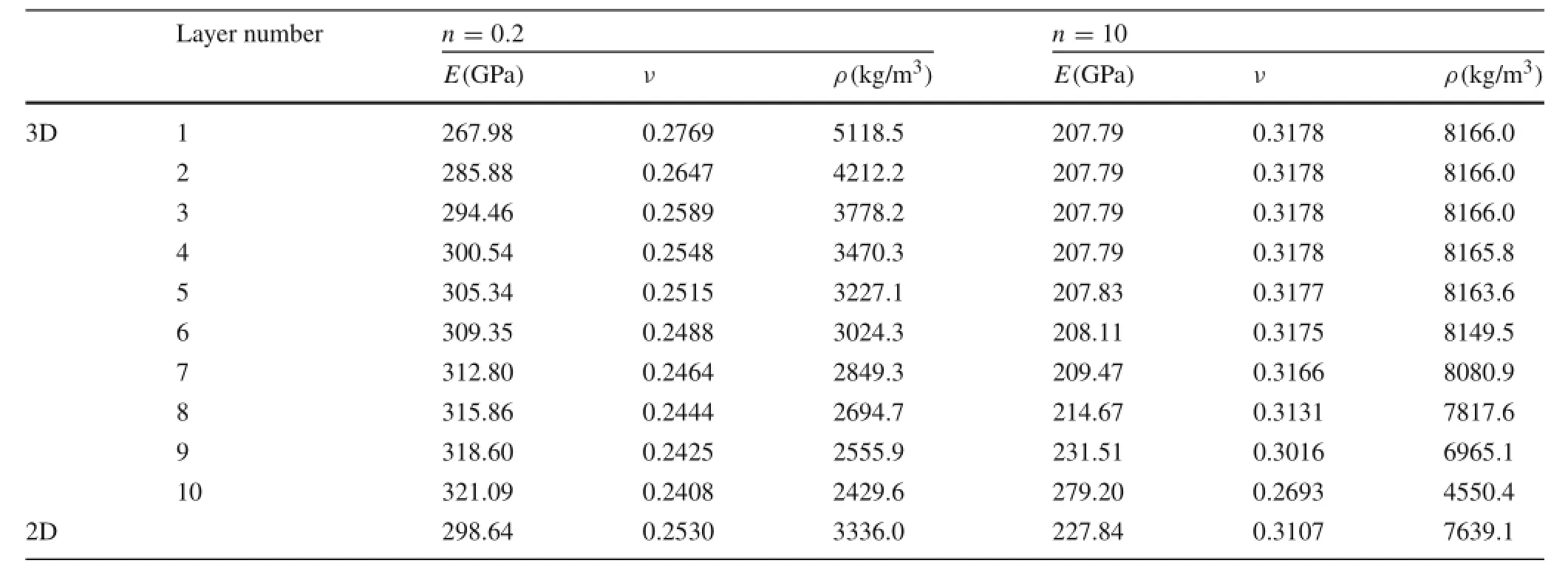
Table 4 Material properties for 3D and 2D FEM models(Type I)

Table 5 Frequency comparisons for Type I FGM square,fully clamped plates(k1,k2)=(0,0)

Eliminating η from Eq.(31)and ϑ from Eq.(32)yields Therefore,we have the two eigenfunctions in terms of the eigenvalues,

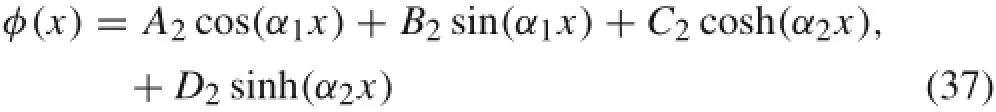
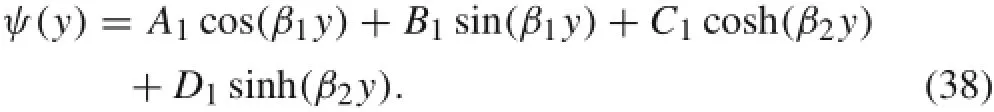
Notably in Refs.[3,4]the authors show that Eqs.(26),(37), and(38)form a general solution of the characteristic govern-ing equation(24)of a thin plate.For the separable boundary conditions as SS,C,and G,two transcendental eigenvalue equations can be derived using two pairs of opposite edge conditions.For any combinations of separable boundary conditions,the methods to derive eigenvalue equations are identical,as shown in Ref.[5].For the pair of opposite boundary conditions with respect to y=0 and b,Table 2 lists the eigenvalue equations and eigenfunctions for all possible combinations of separable boundary conditions,and one can directly obtain the results in the same form with respect to the boundary conditions of x=0 and x=a,as given in Ref.[5].

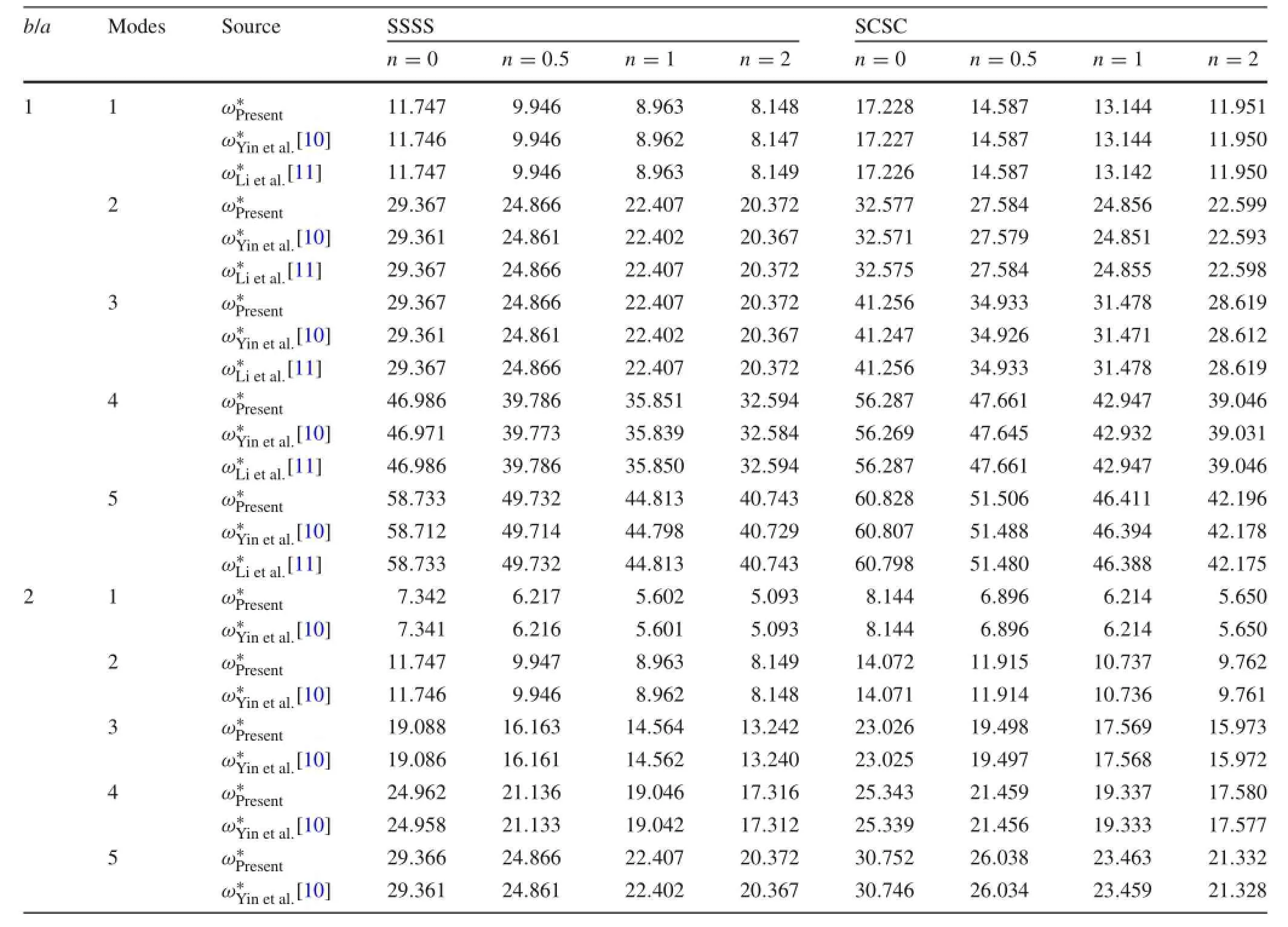
Table 6 Frequency comparisons for Type III FGM plates with different boundary conditions(a/h=100),(k1,k2)=(0,0)

Table 7 Frequency comparisons for Type II FGM(n=2)square,fully clamped plates(k1,k2)=(0,0)

It should be noted that the transcendental equations can be solved by the Newton–Raphson method without any difficulty;since it just like the beam case,the authors have thus far not encountered problems in connection with missing roots or other issues.

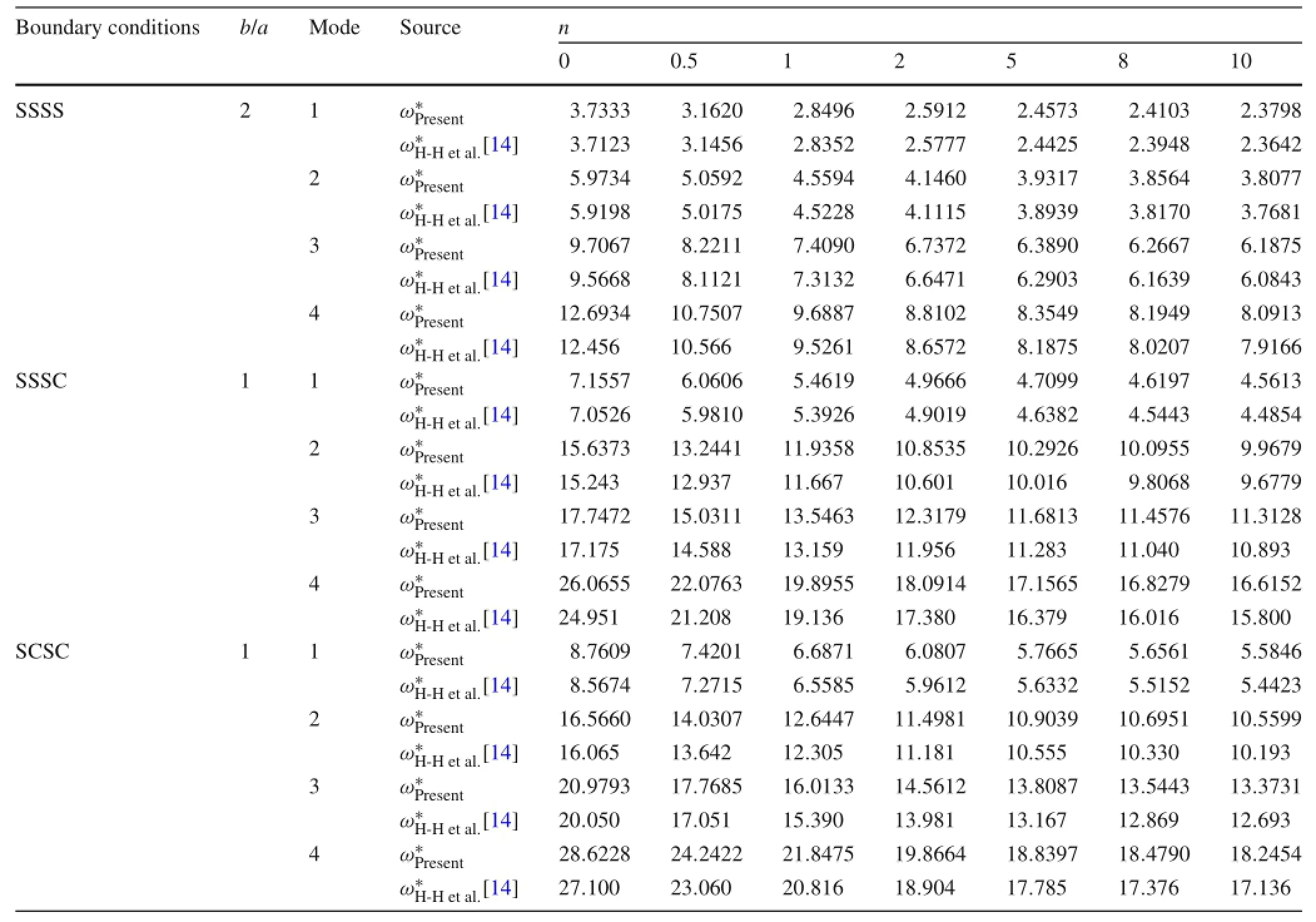
Table 8 Frequency comparisons for Type III FGM plates with different boundary conditions(a/h=20),(k1,k2)=(0,0)

4 Numerical results

This section contains two parts.First,accuracy and comparison studies are carried out.The present results are compared with finite element method(FEM)results and those in the literature.The comparisons show the high accuracy of the present solutions.Second,the effects of the power law index n and aspect ratio a/b on the frequency of FGM plates are investigated,and comprehensive numerical results are presented in dimensionless tabular.

In the following numerical comparisons,three types of FGM plate are taken into account(Table 3).The boundary conditions of the FGM plates are shown in Fig.2.

4.1 Numerical comparisons

This section aims to validate the accuracy of the closed-form solutions by comparing the present results with those in the literature and FEM results obtained by the authors using MSC NASTRAN.To validate the accuracy of the proposed solution method,the linear vibrations of isotropic plates as well as FGM plates without initially stressed and elastic foundations are investigated first.

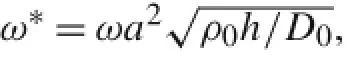
For comparison,the relative difference percentages[%= (NASTRAN–present)/present×100]are also given in Table 5,where the ω*with subscripts FEM2D and FEM3D represent the NASTRAN results obtained using 2D bending panel element with a 50×50 mesh and 3D solid element with a 50×50×20 mesh,respectively.The material properties used in the FEM models are presented in Table 4.

Table 5 shows that the present results are highly accurate. The biggest differences occur for the first-order frequency, in which only a half-wave is included in the mode shape. From Table 6 we can see that the present results and those in Refs.[10,11]are in excellent agreement.In fact, for the cases presented in Table 6,the present results are exact.

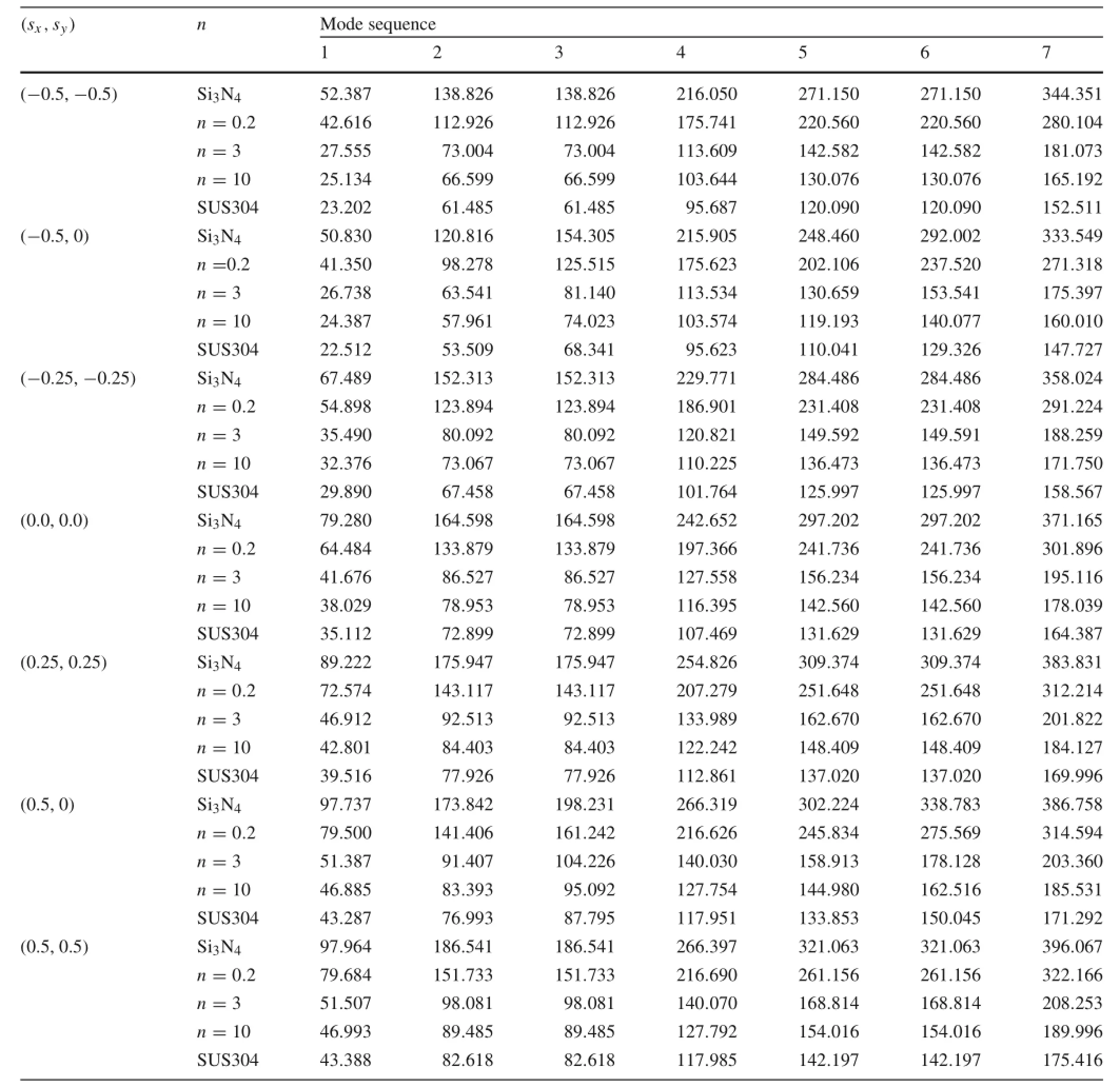
Table 9 Frequency parameterω∗for initially stressed CCCC isotropic and(Type I)FGM square plates without elastic foundations(k1,k2)=(0,0)

The comparisons in Table 5 also show that,as for SUS304, the present solutions agree well with those of Yang and Shen [6],but for Si3N4plates,the present solutions do not;this problem is investigated in Appendix 1,where the authors validate the correctness of the present formulation by analyzing the frequency ratios.

In the foregoing comparisons with results based on CPT and 3D FEM results,it can be concluded that the present results are highly accurate.In the following,we compared our results with those based on shear deformation plate theory (Tables 7 and 8).

In Table 7,the results for Type II FGM(n=2,a=0.2) square plates are compared with those of Kim[17]using the Rayleigh–Ritz method.Note that the present results are in good agreement with those of Kim[17]especially when a/h is greater than 20.

In Table 8,the first four natural frequencies of Type III FGM plates were obtained for three cases of boundary conditions(SSSS,SSSC,and SCSC)and n=0,0.5,1,2,5,8,10. The comparisons reveal that the present results are slightly larger than those of Hosseini-Hashemi et al.[14];this is rea-sonable because that method[14]is based on FSDT and the present method is based on CPT.

Table 10 Frequency parameter ω∗for initially stressed CCCC isotropic and Type I FGM square plates resting on Winkler elastic foundations (k1,k2)=(5,0)

Based on the comparisons presented in this subsection,the high accuracy of the present formulation and present results are validated.

4.2 Parameter study

After verifying the accuracy of the present formulation,parameter studies are carried out to investigate the effects of the power law index n and aspect ratio a/b on the frequency of FGM plates.In this subsection,the same natural frequency parameter as that in Table 5 is used.

Tables 9,10,and 11 give the natural frequencies of prestressed CCCC Type I FGM square plates,in which SUS304 and Si3N4are isotropic,and the other three cases are for n=0.2,3,10.

The in-plane loads are given byFive initialin-plane loading conditions are involved;sx=sy=0 denotes no in-plane loads;sx=0.5 and sy=0 denote uniaxial tension,and sx=sy=0.25 (or 0.5)denotes equal biaxial tension;sx=−0.5 and sy=0 denote uniaxial compression,and sx=sy= −0.25(or−0.5)denotes equal biaxial compression.

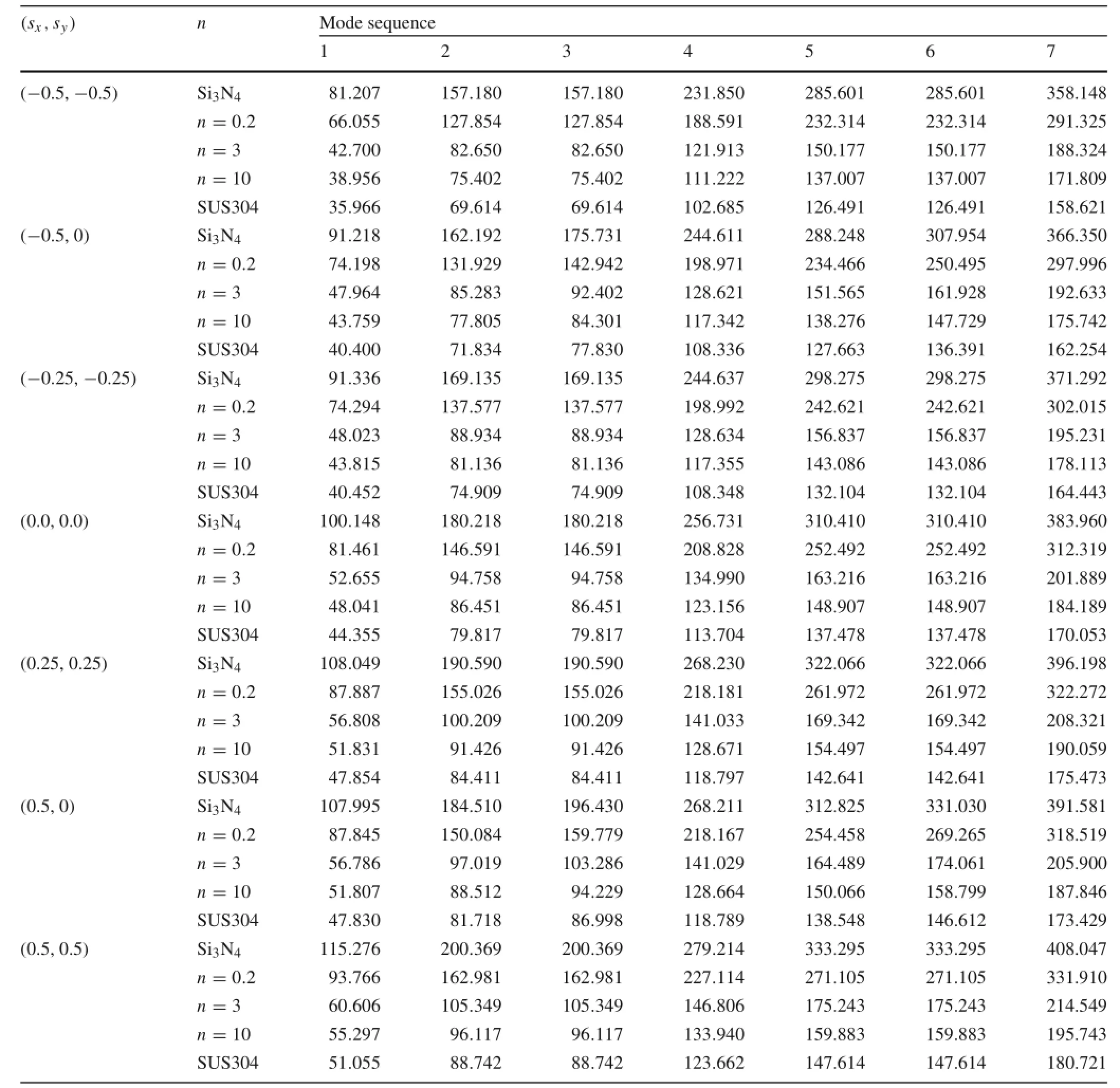
Table 11 Frequency parameter ω∗for initially stressed CCCC isotropic and Type I FGM square plates resting on Pasternak elastic foundations (k1,k2)=(5,1)

The elastic foundations are involved by using(π/a)4k1and.Three types of elastic foundation are taken into account:(k1,k2)=(5.0,1.0)is for the Pasternak model,(k1,k2)=(5.0,0.0)is for the Winkler model,and(k1,k2)=(0.0,0.0)is for plates with no elastic foundation.It can be seen that the frequencies become small when the material composition varies from pure Si3N4to pure stainless steel.As expected,the frequency parameters of plates subjected to initial in-plane tension are much higher than those that are initially compressed.Additionally, the natural frequencies increase as the foundation stiffness increases.

Table 12 presents natural frequencies for Type IFGM rectangular plates with different boundary conditions(SSCC,GGCC,SCCC,CCCG,SGCC,and CCCC,as shown in Fig.2)and different values of the plate aspect ratio a/b(=0.5,0.75,1.0,1.5)and the volume fraction index n(=0.2,3,10).It can be seen that the CCCC rectangular plate has the highest frequencies,whereas the GGCC plate has the lowest.Meanwhile,the dimensionless frequency parameters increase as a/b increases from 0.5to1.5anddecreaseasnincreasesfrom0.2 to 10.

Table 12 Frequency parameter ω∗for Type I FGM rectangular plates with different boundary conditions

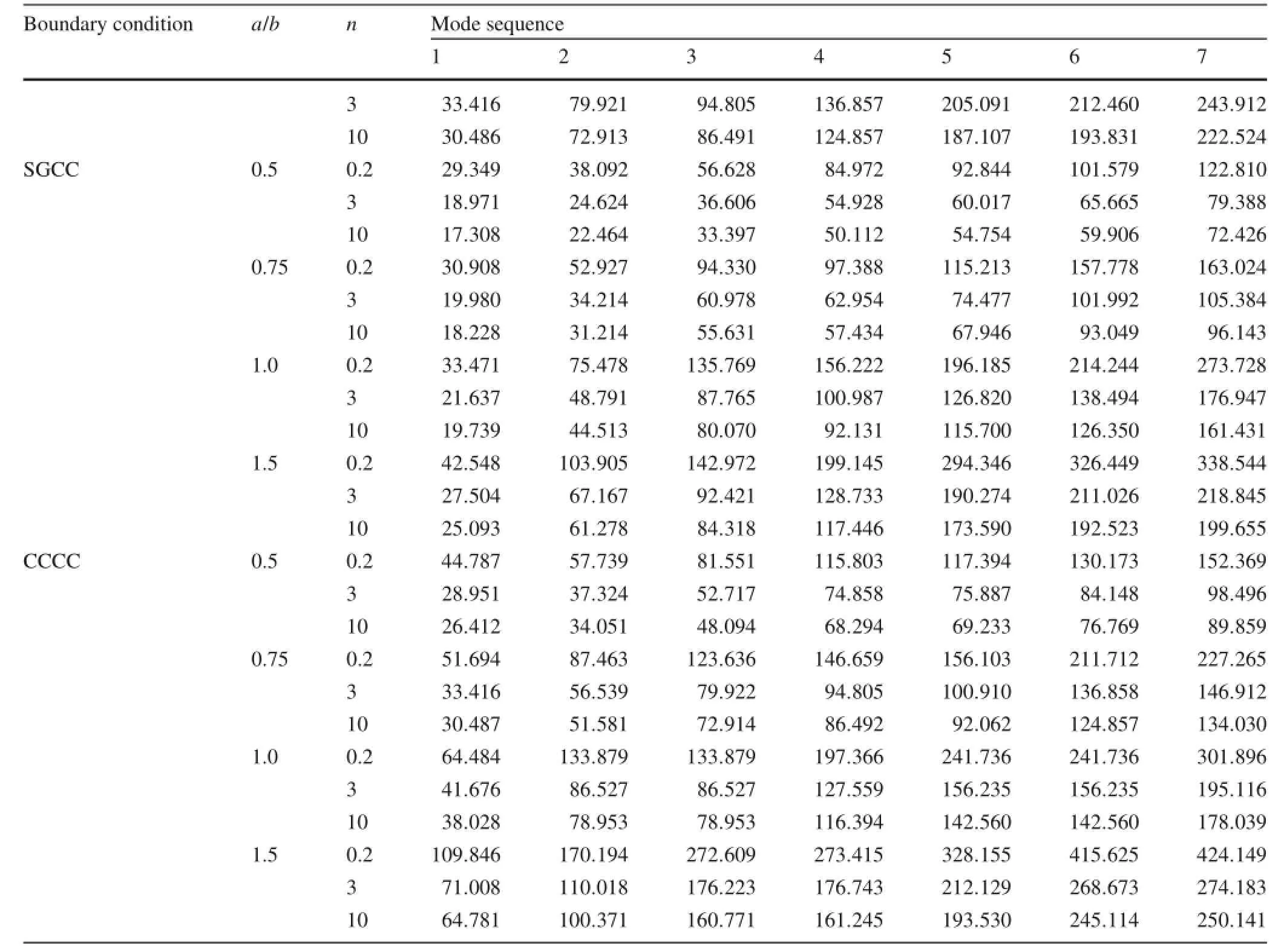
Table 12 continued

Numerical results show that the dimensionless frequency parameters increase as a/b increases and decrease as n increases.Further,the foundation stiffness and initial stress also significantly affect the vibration of FGM plates.Comprehensive numerical results for FGM rectangular thin plates with two adjacent clamped edges subjected to initially inplane loads without or resting on elastic foundations are presented in dimensionless tabular form.

5 Conclusions

In the present study,a frequency analysis of initially stressed FGM rectangular thin plates subjected to in-plane loads and with elastic foundations was analytically conducted.Hamilton’s principle was used to derive the equations of motion based on CPT.A neutral surface was adopted to eliminate the stretching–bending coupling in the FGM plates, and the resulting governing equations of the FGM thin plates have the same forms as those of homogeneous thin plates.

From the study one may conclude that a constant Poisson’s ratio is the condition for the existence of a neutral surface;in this sense,the neutral surfaces of the material elastic properties are the same,but they are not the same like a mass neutral surface.For real FGM plates,Poisson’s ratio cannot be constant;therefore,the material neutral surface is not pos-sible in reality,that is,the theory based on a neutral surface is approximate.

As for FGM rectangular plates with separable boundary conditions,including plates with two adjacent clamp supports,closed-form solutions for the problem of free vibrations of rectangular FGM thin plates were obtained using a separation-of-variables method.The obtained normal mode functions and frequency equations are in an elegant closed form.The present solutions were validated by comprehensive comparisons with those in the literature.

Comprehensive numerical results show that dimensionless frequency parameters increase as the aspect ratio a/b increases and decrease as the power law index n increases. Furthermore,the foundation stiffness and initial stress also significantly affect the vibration of FGM plates.

Acknowledgments The project was supported by the National Natural Science Foundation of China(Grants 11172028,1372021),Research Fund for the Doctoral Program of Higher Education of China(Grant 20131102110039),and the Innovation Foundation of Beihang University for PhD graduates.

Appendix 1

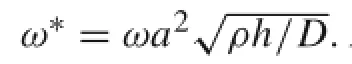
have

From Eq.(24)one finds that the frequency parameterω∗is the same for thin plates with different materials since the elastic foundation and in-plane loads are not taken into account here,that is

Substitution of Eq.(A1)into Eq.(A2)yields

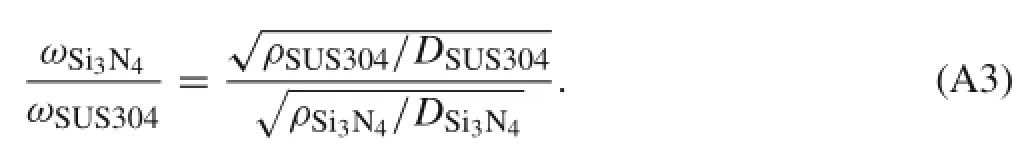
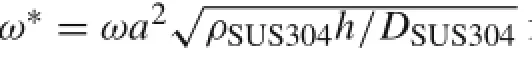
from which we have

To substitute the material properties of SUS304 and Si3N4as given in Table 3 into Eq.(A3),and to substitute the ensuing results into Eq.(A5),one can obtain that the ratio of the frequency parameter ω∗between Si3N4and SUS304 is 2.2579(Table 13).In Sect.4.1,we use the same dimensionless natural frequency parameter as Yang and Shen[6] in numerical comparisonswhich is also 2.2579(Table 13);therefore,it can be concluded that the present results are correct.But using the numerical results of Yang and Shen[6]is 1.2164,and this shows that some numerical results of Yang and Shen[6]may not be correct.

Appendix 2

The differential operators in Eq.(18)are as follows

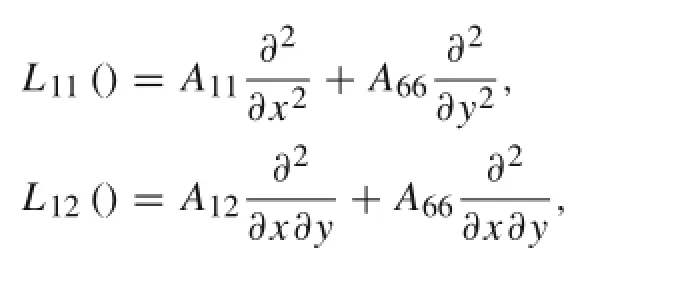
Table 13 Frequency comparisons between present method and that of Yang and Shen[6]for Type I FGM plates

And the boundary conditions derived using Hamilton’s principle have the following forms:

The shear forces are given by following relations:

References

1.Koizumi,M.:The concept of FGM.Ceram.Trans.Func.Grad. Mater.34,3–10(1993)

2.Koizumi,M.:FGM activities in Japan.Compos.PtB.Eng.28,1–4 (1997)

3.Xing,Y.F.,Liu,B.:New exact solutions for free vibrations of rectangular thin plates by symplectic dual method.Acta.Mech.Sin. 25,265–270(2009)

4.Xing,Y.F.,Liu,B.:New exact solutions for free vibrations of thin orthotropic rectangular plates.Compos.Struct.89,567–574(2009)

5.Xing,Y.F.,Xu,T.F.:Solution methods of exact solutions for free vibration of rectangular orthotropic thin plates with classical boundary conditions.Compos.Struct.104,187–195(2013)

6.Yang,J.,Shen,H.S.:Dynamic response of initially stressed functionally graded rectangular thin plates.Compos.Struct.54, 497–508(2001)

7.Abrate,S.:Free vibration,buckling,and static deflections of functionally graded plates.Compos.Sci.Technol.66,2383–2394 (2006)

8.Abrate,S.:Functionally graded plates behave like homogeneous plates.Compos.Pt B.Eng.39,151–158(2008)

9.Zhang,D.G.,Zhou,Y.H.:A theoretical analysis of FGM thin plates based on physical neutral surface.Comput.Mat.Sci.44,716–720 (2008)

10.Yin,S.,Yu,T.,Liu,P.:Free vibration analyses of FGM thin plates by isogeometric analysis based on classical plate theory and physical neutral surface.Adv.Mech.Eng.5,634584(2013)

11.Li,S.R.,Wang,X.,Batra,R.C.:Correspondence relations between deflection,buckling load,and frequencies of thin functionally graded material plates and those of corresponding homogeneous plates.J.Appl.Mech.82,111006(2015)

12.Thai,H.T.,Uy,B.:Levy solution for buckling analysis of functionally graded plates based on a refined plate theory.J.Mech.E.Pt C. 227,2649–2664(2013)

13.Reddy,J.N.,Wang,C.,Kitipornchai,S.:Axisymmetric bending of functionally graded circular and annular plates.Eur.J.Mech.18, 185–199(1999)

14.Hosseini-Hashemi,S.,Fadaee,M.,Atashipour,S.R.:A new exact analytical approach for free vibration of Reissner–Mindlin functionally graded rectangular plates.Int.J.Mech.Sci.53,11–22 (2011)

15.Reddy,J.N.:Analysis of functionally graded plates.Int.J.Numer. Meth.Eng.684,663–684(2000)

16.Yang,J.,Shen,H.S.:Vibration characteristics and transient response of shear deformable functionally graded plates in thermal environments.J.Sound.Vib.255,579–602(2002)

17.Kim,Y.W.:Temperature dependent vibration analysis of functionally graded rectangular plates.J.Sound.Vib.284,531–549(2005)

18.Swaminathan,K.,Naveenkumar,D.T.,Zenkour,A.M.,et al.: Stress,vibration and buckling analyses of FGM plates–a state-of-the art review.Compos.Struct.120,10–31(2015)

19.Thai,H.T.,Kim,S.E.:A review of theories for the modeling and analysis of functionally graded plates and shells.Compos.Struct. 128,70–86(2015)

20.Sayyad,A.S.,Ghugal,Y.M.:On the free vibration analysis of laminated composite and sandwich plates:a review of recent literature with some numerical results.Compos.Struct.129,177–201(2015)

21.Reddy,J.N.,Chin,C.D.:Thermomechanical analysis of functionally graded cylinders and plates.J.Therm.Stresses.21,593–626 (1998)

✉ Y.F.Xing xingyf@buaa.edu.cn

1Institute of Solid Mechanics,Beihang University, Beijing 100191,China

2China Academy of Launch Vehicle Technology R&D Center, Beijing 100076,China

8 January 2016/Revised:3 May 2016/Accepted:21 June 2016/Published online:21 September 2016