A semi-analytical approach for calculating the equilibrium structure and radial breathing mode frequency of single-walled carbon nanotubes

J.Gong·L.Thompson·G.Li

A semi-analytical approach for calculating the equilibrium structure and radial breathing mode frequency of single-walled carbon nanotubes

J.Gong1·L.Thompson1·G.Li1

©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016

A semi-analytical model for determining the equilibrium configuration and the radial breathing mode(RBM) frequency of single-wall carbon nanotubes(CNTs)is presented.By taking advantage of the symmetry characteristics, a CNT structure is represented by five independent variables.A line search optimization procedure is employed to determine the equilibrium values of these variables by minimizing the potential energy.With the equilibrium configuration obtained,the semi-analytical model enables an efficient calculation of the RBM frequency of the CNTs.The radius and radial breathing mode frequency results obtained from the semi-analytical approach are compared with those from molecular dynamics(MD)and ab initio calculations. The results demonstrate that the semi-analytical approach offers an efficient and accurate way to determine the equilibrium structure and radial breathing mode frequency of CNTs.

Carbon nanotubes·Equilibrium structure· Radial breathing mode frequency

DOI 10.1007/s10409-016-0582-2

1 Introduction

In addition to applications in many other areas,carbon nanotubes(CNTs)have shown great potential as a structural material due to their outstanding mechanical properties[1,2]. The mechanical behavior of CNTs have been modeled using both atomistic and continuum methods.While more accurate,atomistic level methods such as ab initio and moleculardynamics(MD)methods are limited to small CNT structures due to their high computational cost.In this regard, continuum level models,such as frame[3–5],shell[6–9],and beam[10,11]models,have been proposed for efficient mechanical analysis of large CNT structures and systems[12].As these continuum models treat CNT as a linear elastic material,equivalent elastic constants such as Young’s modulus and Poisson’s ratio must be determined. Contrary to earlier belief that the elastic constants are insensitive to CNT’s radius and chirality,more recent results have shown otherwise[12].Ab initio calculations indicated that the CNT elastic properties change with different chiralities[13].Results from separate studies showed that the Young’s modulus varies with CNT’s radius,especially when it is small[3,14–16].The study by Wang[17]showed that the bending modulus of CNTs depends on their radius and chirality.The study by Huang et al.[18]further demonstrated theoretically the variation of elastic constants with radius and chirality.Therefore,obtaining equilibrium tube radius,especially for small CNTs,is critical in the continuum models predicting the mechanical behavior of CNTs.

Other than the elastic properties,the dynamic behavior of CNTs is also geometry dependent.A special vibrational mode of CNTs,called the radial breathing mode(RBM),has attracted much attention recently as it can serve as the“fingerprint”of CNTs[19].In Raman spectroscopy of CNTs,there are four Raman bands that are strongly resonance enhanced. One is the RBM,in which all carbon atoms are vibrating along the radial direction[20].It has been shown that the RBM frequency is highly dependent on the tube radius[21], leading to the idea that it can be used to identify the radius and chirality of a given CNT sample.However,a CNT’s radius varies with its chirality and CNTs with different chiralities may have similar radii.The effectiveness of the RBM fre-quency based CNT identification relies on an accurate model describing the relations of the radius,chirality,and RBM frequency of CNTs.

Many models have been developed for obtaining the equilibrium structure of CNTs.A popular approach is the simple rolling approach.There are two rolling methods in the simple rolling approach,namely cylinder model and skeleton model(or ball-and-stick model)[22].The cylinder model rolls a graphene sheet into a CNT like a piece of paper.This method assumes that the carbon atoms and bonds are all on the cylindrical surface after rolling,which implies curved bonds in the CNT.To eliminate this artificial effect,the skeleton model assumes that the bonds remain straight with fixed length during the rolling process.However,in actual cases, due to the symmetry breaking in the rolling process,both the angle and length of the bonds are adjusted to reach the minimum potential energy of CNT.Therefore,the assumptions in the simple rolling models are not accurate[13,22],especially for CNTs with small radius.The interactions between the atoms must be accounted for in the determination of a CNT’s equilibrium structure.In this regard,MD or first principle simulations haven been employed to relax the structure of CNT.The balanced atomic structure can be obtained by minimizing the potential energy of CNTs.While these atomistic methods are more accurate than the simple rolling approach,their computational cost is typically very high. To obtain efficiently and accurately the equilibrium geometry of CNTs,Jiang et al.[23]developed a lattice mechanics model with five independent lengths representing the geometry of a CNT.However,since the potential energy cannot be explicitly expressed in terms of these five length variables,their method still largely relies on a numerical solution of the nonlinear system.For the RBM frequency analysis, several models have been proposed to calculate the relation between the RBM frequency and the tube radius[19].Most of the resent results are based on the tight-binding approximation[24,25],zone folding force constant model[26,27], ab initio calculations[20,22,28],and molecular structural mechanics models(i.e.,stick-spiral models)[29–31],which consider the energies from bond stretching,bond twisting, and bond angle variation separately.These models are either complex and computationally expensive or less accurate due to neglecting the multi-body interactions among the carbon atoms.

In this work,we present a semi-analytical model for obtaining the equilibrium geometry and RBM frequencies of single-wall CNTs.The model employs two bond lengths along with three bond angles as independent variables,which enables analytical differentiation of interatomic potential functions.With the analytical expressions of the derivatives, the equilibrium geometry of CNTs can be obtained by using an energy minimization procedure,which is performed by using the conjugate gradient optimization method.Having obtained the equilibrium geometry of the CNTs,the RBM frequencies can be calculated analytically for a given multibody potential,which,to the authors’best knowledge,has not been done previously in the literature.While the model is general,extremely efficient,and applicable to different multi body potentials,its effectiveness is demonstrated by using the reactive empirical bond order(REBO)potential[32].

The paper is organized as follows.Section 2 describes the general method for calculating the equilibrium configuration of CNTs.Section 3 illustrates the analytical calculation of RBM frequencies.The radius and RBM results are presented and discussed in Sect.4.Finally,the conclusions are given in Sect.5.

2 Semi-analytical model for calculating equilibrium configuration of CNTs

2.1 CNT geometry

A sufficiently long single-wall CNT with open ends can be regarded as a pattern of repeating two-atom unit cells except for a small region close to the ends.Moreover,in each unit cell,there is a so-called C2-axis rotational symmetry[22],as shown in Fig.1.Because of the C2-axis rotational symmetry, a unit cell can be defined by one atom with its three nearest neighbors.It is often more convenient to represent the atom positions by using bond lengths and angles.Therefore,as shown in Fig.1,given the position of any atom with the lengths(denoted as r)and angles(denoted as θ)of its three bonds,the entire structure of a CNT can be determined.

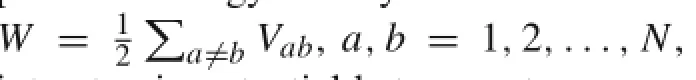
2.2 Geometric mapping

Although the skeleton model does not provide an accurate prediction of CNT radius,it offers a starting point to represent different types of CNTs.The skeleton model assumes that each C–C bond behaves as a rigid rod connecting two carbon atoms on the cylindrical surface.The mapping between a CNT and its corresponding flat graphene is illustrated in Fig.2.As shown in Fig.2a,the bold dashed line represents

Fig.1 CNT:unit cell and C2-axis symmetry the chiral vector direction(i.e.the rolling direction)of the 2-D graphene.The bond angles,α1,α2,and α3,are defined with respect to the chiral vector.The positions of the three nearest neighbors of the center atom a are defined by the horizontal and vertical distances,l and h,from the center atom.Figure 2b shows the 3-D positions of the four atoms after they are rolled into a CNT.The black circle represents the cross section.The positions of the three neighbor atoms are also defined by the horizontal and vertical distances from the center atom.An example of a chiral(or rolling)vector (4,1)for rolling into a(4,1)CNT is shown in Fig.2c.Since in the simple rolling step,the bond lengths rj,and the distances hj=rjsinαj,lj=rjcosαjremain the same,it is obvious that the three chord lengths in Fig.2b are equal to l1,l2,and l3,respectively.In the simple rolling model,given the chiral vector(N,M),the radius of a carbon nanotube can be determined by:

where ac−cis the C–C bond length in a 2-D graphene sheet. Because of the asymmetric inter-atomic interactions between the carbon atoms,the bond lengths and angles are no longer the same in a CNT.For this reason,further analysis is necessary to determine the equilibrium bond lengths and angles.

As shown in Fig.2b,the central angles of the chords in the cross-section circle are

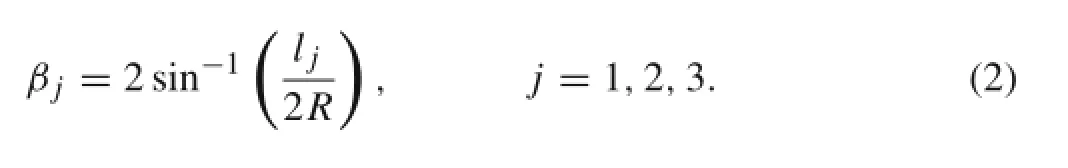
In order to for ma closed cylindrical surface,atom a and atom a′in Fig.2c must be the same atom.It is easy to show that two geometric conditions must be satisfied:(1)the summation of the central angles of all corresponding chords(i.e.,the βs)should be 2π and(2)the distance between atom a′and the chiral vector should be zero.Mathematically,the first condition leads to

Fig.2 Geometric mapping of a CNT.a Carbon atoms in 2-D graphene.b Atoms mapped onto a CNT.c Rolling of a(4,1)CNT

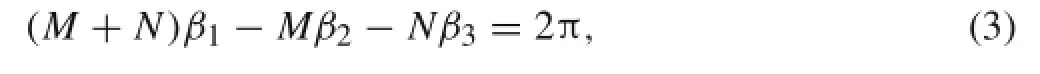
where M and N represent the chirality of a(M,N)CNT. The second condition can be written as

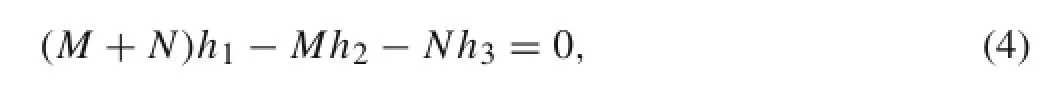
which gives

The angle between bonds j and k,θjk,can then be calculated by(see Appendix 1 for details)

where

With the graphene-to-CNT mapping described above,the original potential energy function of a CNT unit cell, w0(r1,r2,r3,θ12,θ23,θ13),can be rewritten in terms of seven variables:w0=w(R,r1,r2,r3,α1,α2,α3).Then,the bond angles,θjk,can be replaced by R,r1,r2,r3,α1,α2,α3following Eq.(6).Furthermore,R is an implicit function of r1,r2,r3,α1,α2,α3,according to Eq.(3).Equation(5) shows that r3can be expressed in terms r1,r2,and the angles. Therefore,the potential energy can be expressed in terms of five independent variables as

where the variable vector x={r1,r2,α1,α2,α3}.

2.3 Equilibrium structural configuration

To determine the actual radius of the CNT,it is necessary to calculate the equilibrium configuration of the carbon atoms.An energy minimization procedure using a line search method is adopted to determine the equilibrium configuration.Iteratively,a line search method determines a search direction and then performs single variable minimization to obtain the minimum position along the search direction.In this work,in light of the general form and typical behavior of C–C interatomic potentials,a first order conjugate gradient method[35]is employed to determine the search direction, and the Powell method[36]is used to carry out the single variable optimization along the search direction.

The conjugate gradient method starts with a steepest descent calculation.The initial bond lengths are set to beand the initial angles are given by

Therefore,the starting point of the optimization is x0=.The gradient of the potential energy function can be obtained using

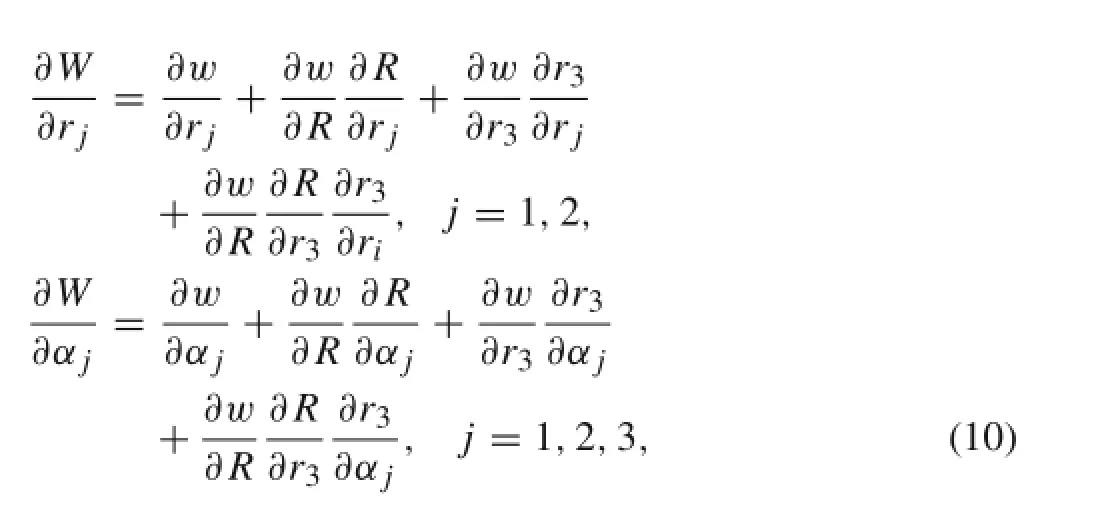
where

The derivatives of cosθjk,j,k=1,2,3,j/=k can be obtained from Eq.(6)

The derivatives of R and r3can be obtained from Eqs.(3) and(5)as

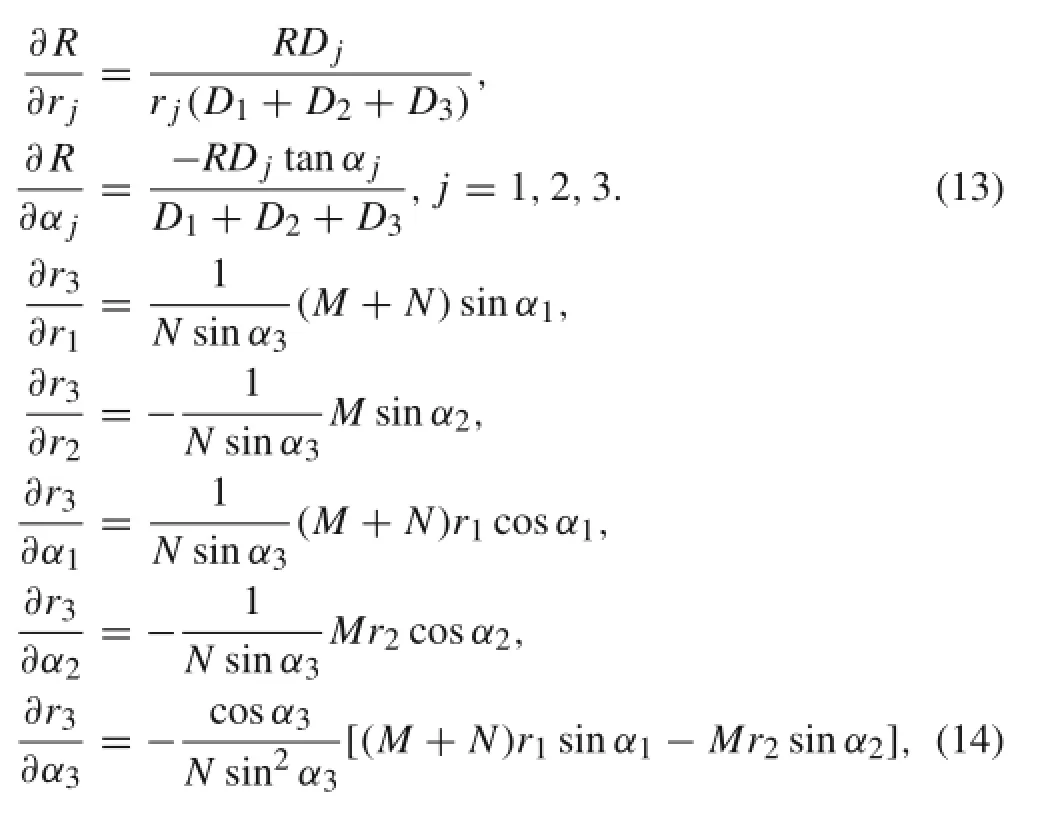
where

The general procedure of the energy minimization is described as follows.For a given step k(k=0,1,2,...,K−

1,where K is the number of variables),the objective is to compute a new position vectortoward the minimum point of the potential function.For k=0,x0is the initial position vector given by.Next, a single variable objective functionwhereis minimized along the C0direction.Assuminggives the minimum of,the position vector x is updated asFor k＞0, Ckis obtained by using the conjugation constraint,which requires that the new search direction be orthogonal to the previous search directions:

where Ck−1is the search direction in the previous step,gkis the negative gradient of the potential function

and

Once the search direction is computed,the next position vector is determined by minimizing the potential energy function along the search direction,i.e.

Note that k＜K since there can only be as many as K vectors in an orthogonal set in a K-dimension space.If the algorithm does not converge within K steps,the procedure is started over again by taking xKas the new x0.The iterations continue until the convergence criterion is met.

In this work,the Powell method[36]is employed to solve the single variable minimization problem and obtain ηmin. The Powell method approximates the actual function by using a quadratic function.The quadratic function is determined by fitting the actual function near its minimum.As most of the interatomic potential energy functions are smooth near the equilibrium position,performance of the quadratic approximation is found to be satisfactory.To determine the quadratic function,the potential function is sampled at three different locations.The first two are given byandA common choice of the step size is δη=0.5.The third point is obtained based on the potential energy function values at the two ends as

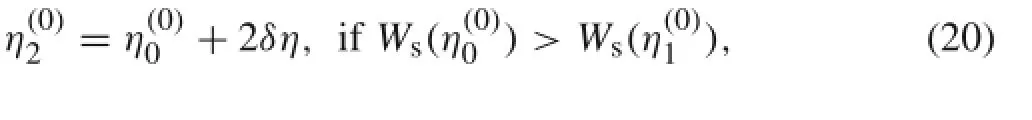
where

The location of the minimum of f(η)is obtained as

Note that the second term on the right hand side of Eq. (24)is used to preventfrom falling too far from the current interval.Onceis obtained,the convergence criteria are checked.The minimum is found if both

where∈fand∈ηare the termination tolerances for Wsand η,respectively.If any of the convergence criteria are not satisfied,a new iteration starts.Ifis updated to beand a new set of threepoints are determined.The new set is selected fromand the old set,such that it consists ofand two η values that are closest toWith the new η point set,the procedure from Eqs.(22)–(24)is repeated to calculate.The iterations continue until the convergence criteria are satisfied and the minimum of Ws(η)is found.

The iterative procedure continues until the negative gradient‖gk‖＜∈g,where∈gis the global convergence tolerance. The CNT potential energy minimization procedure is summarized in Algorithm 1.

3 RBM frequency

Algorithm 1 Algorithm for CNT potential energy minimization

In this work,having obtained the equilibrium structural configurations of CNTs as described in Sect.2,the RBM frequencies are further calculated using the multi-body inter atomic potential energy of the carbon atoms.The primary assumption is that,when a CNT vibrates in RBM,all atoms move only in radial direction and remain on a cylindrical surface as shown in Fig.3.That is,the mode coupling effect is negligible[22,28].

Based on this assumption,the relation between bond lengths,bond angles,and tube radius in RBM can be established as

where ri,αi,li,and hi,i=1,2,3,are defined in Sect.2.1. The superscript 0 denotes the equilibrium configuration.rican be explicitly expressed as

Fig.3 RBM vibration of CNTs

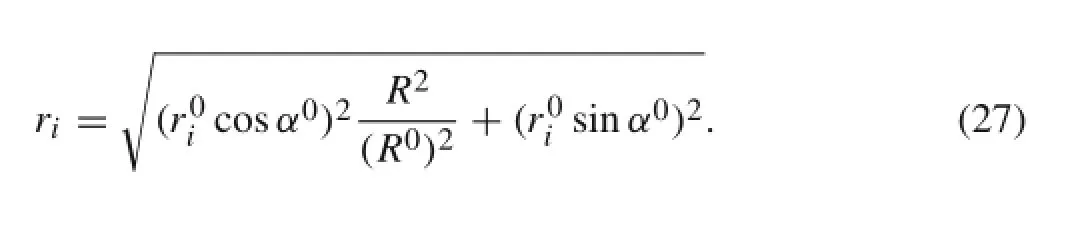
By using Eq.(27),Eq.(6)can be rewritten as

Note that,S,H,and T are all independent of R.Thus,the 1-st and 2-nd order derivatives of riand cosθjkwith respect to R are derived as follows

where w0is the potential energy per,and i,j,k,l=1,2,or 3.The RBM frequency is given by

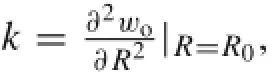
4 Results and discussion

To demonstrate the performance of the model,the semianalytical approach is applied to the REBO potential[32]tocalculate the equilibrium configuration and RBM frequency of various CNTs.The REBO potential has been widely used in MD and lattice dynamics(LD)simulations of CNTs.It should be noted that while the detailed formulation for the REBO potential is presented in Appendix 2,the application of the method to other C–C interatomic potentials is straightforward by using the approach and following the steps listed in Algorithm 1.

4.1 Radius of CNTs

In this section,the radii of a set of CNTs with different chiralities are computed by using the semi-analytical model.For the purpose of model validation,the computed results are compared with those obtained from MD simulations.The MD simulations are preformed using the lammps and gromace(LAMMPS)package.The REBO potential with the parameters given in Table A1(Appendix 2)is adopted in the semi-analytical calculation and MD simulations.In the test cases,the CNT chiralities varies from(4,0)to(8,4).In MD simulations,the length of the CNTs is set to be around 20 nm.It is verified that further increasing the length does not change the results. The MD simulation box size is set to be 20 nm×20 nm in the transverse(cross-sectional)directions and 40 nm in the longitudinal direction with free boundary conditions applied.The total linear momentum and angular momentum are fixed to be zero.With a time step of 0.2 fs,the system is initialized at5 Kand then the temperature is reduced to 0.01 K under the canonical ensemble(NVT) with 3×105time steps.A drag value of 0.5 is applied to increase damping.The purpose of this drag value is to damp unwanted pressure oscillation when applying a Nose/Hoover thermostat.The tube radius is calculated as the average distance between carbon atoms and the tube axis.Bond angles, bond lengths,and the radii are averaged on atoms within 20%length at the tube center to reduce influence of the free ends.

Bond length,bond angle and radius results of the CNTs obtained by using the semi-analytical method and MD simulations are compared in Tables 1,2,and 3.It is clear that the results obtained from the two methods match very well. The maximum difference is less than 0.2%.Results show that the C–C bond lengths increase as the radius decreases, and the difference between the bond lengths r1,r2,and r3increases as well.For the smallest(4,0)nanotube,the largest bond length is 1.451 Å(1 Å=0.1 nm),which is 2%larger than the bond length in graphene,1.420 Å.The variation of bond lengths is due to the change of bond angles.Rolling a graphene sheet into a tube makes the angles between bonds smaller than 2π/3,which increases the potential energy.This excess energy is then partially relaxed by an expansion of the atomic lattice structure,leading to elongation of the bonds.Therefore,the smaller the radius,the smaller the angles,and the larger the expansion.This conclusion is consistent with previous observations reported in Ref.[13].

Table 4 further compares the radius results with those obtained from the simple rolling model and two different ab initio calculations.It is shown that the semi-analytical model with REBO potential gives nearly identical results to the MD simulations,but with much less computational cost. The error of the simple rolling model is obvious.As shown on Fig.4,the relative difference between the relaxed radius and the simple rolling radius R0increases as the radius decreases. The results indicate that the simple rolling model is inappropriate in determining the equilibrium configuration of CNTs, especially for nanotubes with small radius.For example,for the(4,0)nanotube,we obtain a radius that is 9%greater than R0.Furthermore,it is shown that the chirality play an important role on the results.The armchair CNTs show smaller relative errors than the zigzag CNTs.For other chiral nan-otubes,the radius error resides within the zone between the zigzag and armchair CNTs.It is observed that the orientation of the unit cells determines how the bond angles are affected by rolling,which results in different radius expansion for different chiralities.It should be noted that there is a small difference between the semi-analytical model andab initio results.This is due to the difference between the REBO potential employed in the semi-analytical model and the electron density functionals used in the ab initio calculations.

Table 1 Bond lengths,bond angles,and radius of zigzag CNTs

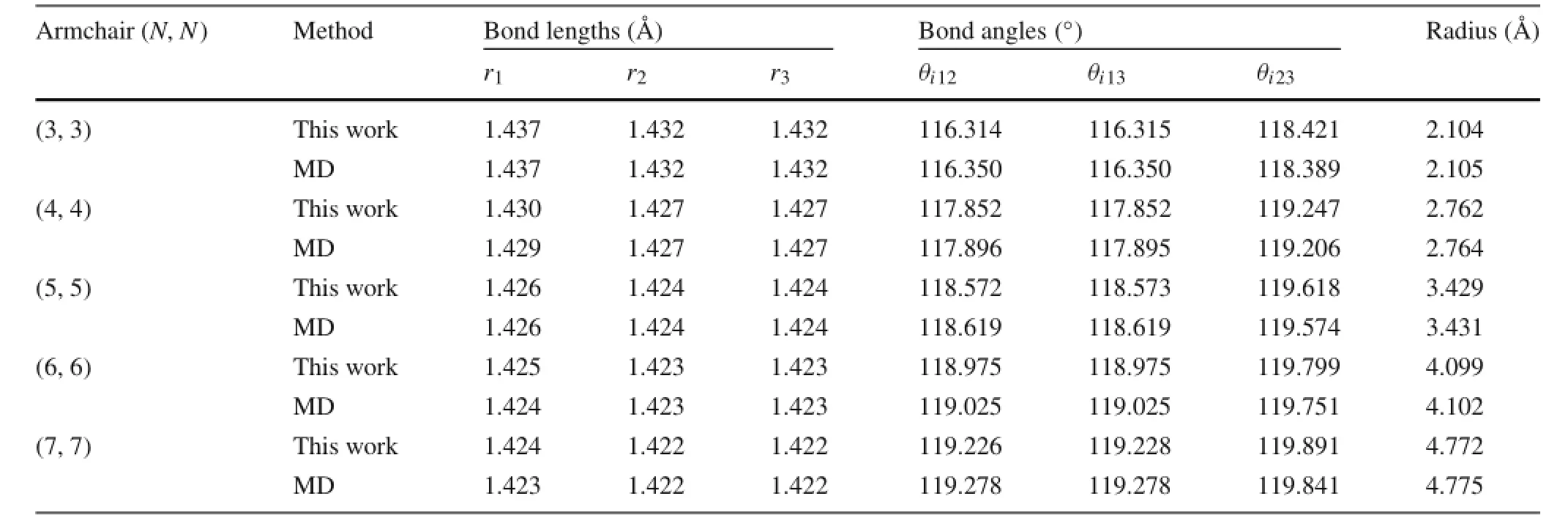
Table 2 Bond lengths,bond angles,and radius of armchair CNTs

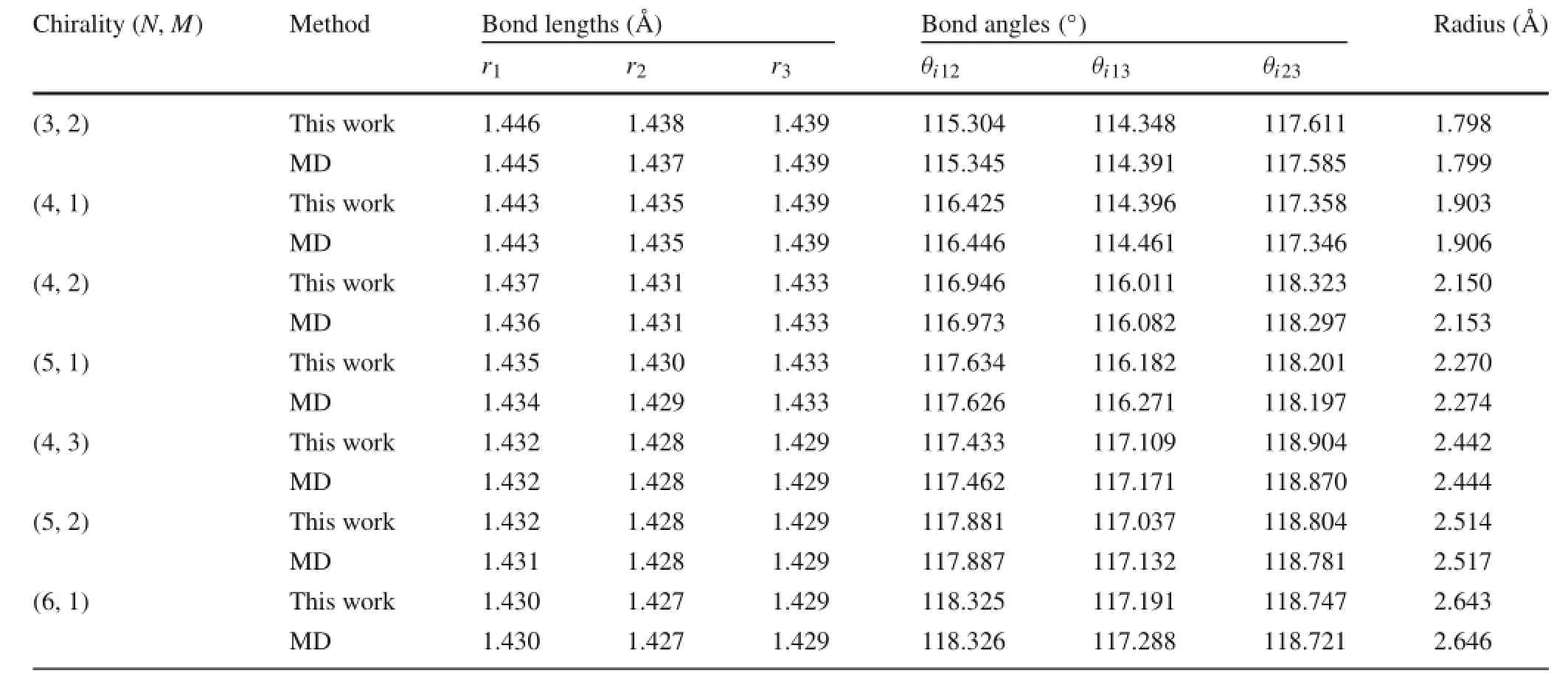
Table 3 Bond lengths,bond angles,and radius of chiral CNTs

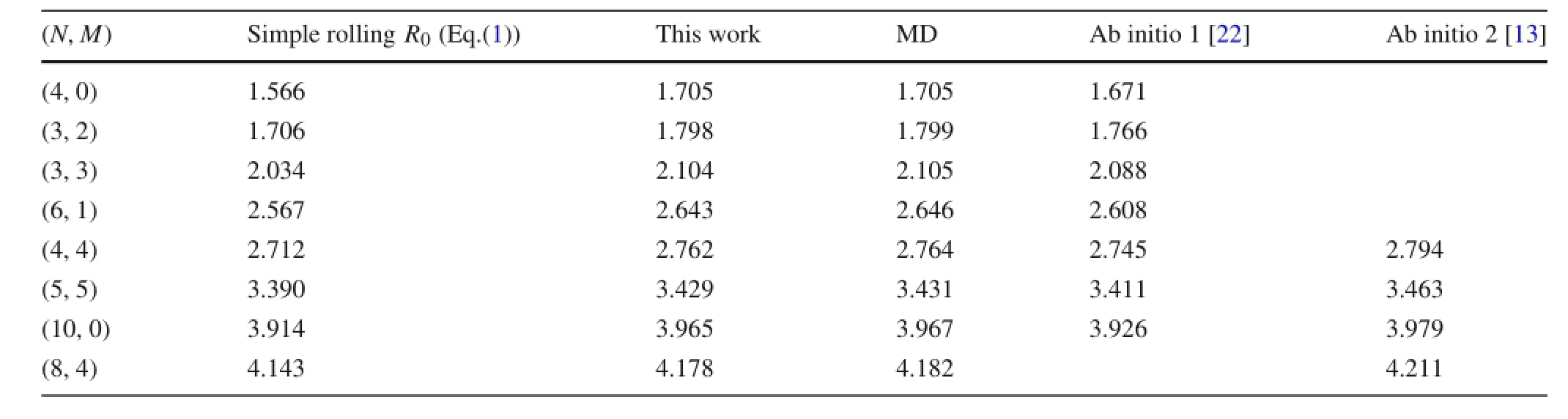
Table 4 Comparison of radius results obtained from different methods

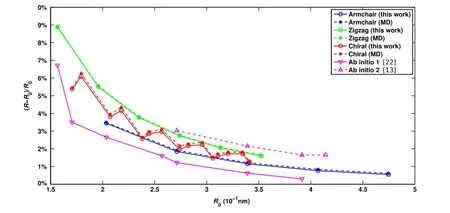
Fig.4 Percentage difference between the simple rolling radius R0and the radii calculated from the semi-analytical,MD,and ab initio models

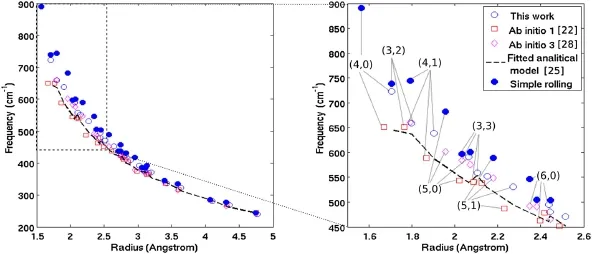
Fig.5 RBM frequencies(Hz/speed of light)of CNTs.The two ab initio results(ab initio 1[22]and 3[28])are obtained from the literature

4.2 RBM frequency of CNTs

Having obtained the equilibrium structure of the CNTs,the RBM frequencies are calculated as described in Sect.3.Figure 5 shows the RBM frequencies of a variety of CNTs calculated by using the semi-analytical,simple rolling,ab initio approaches,as well as a fitted analytical model[25]. For the sake of clarity,the calculated data points for narrow CNTs are enlarged and displayed on the right side of Fig. 5.The REBO potential with the parameters given in Appendix 2 is used in the semi-analytical approach.As shown in Fig.5,significant differences in the results are observed for narrow CNTs with radius smaller than 2.6 Å.The difference between the semi-analytical and simple rolling approaches is largely due to the inaccurate geometry properties(radius, bond lengths,and angles)given by the simple rolling model. The error in these geometry properties is further enlarged in the RBM frequency results due to the high sensitivity of the force constants(second derivatives of the interatomic potential)to the tube geometry.Figure 5(right)shows that such error in the simple rolling model results is more than 20%for the(4,0)CNT.The difference between the semianalytical and ab initio results stems from the difference in their physical description of the interatomic interactions (i.e.,interatomic potentials vs electron density functionals). It should be noted that the results from“ab initio 3”[28]are based on tube geometries obtained from the simple rolling model.Finally,while Fig.5 shows that the differences in the RBM frequency results from the different models become negligible for tubes with radius larger than 4 Å,it is worth pointing out that for CNTs of larger sizes,the semi-analytical approach is orders of magnitude faster than the lattice dynamics,MD,and ab initio methods.

5 Conclusions

In this work,a semi-analytical unconstrained energy optimization model with five independent variables for determining the equilibrium configuration and the RBM frequency of single-wall CNTs is presented.For demonstration purpose, the semi-analytical model is applied to the REBO potential for the calculation of the radii of various CNTs.It is shown that with a negligible computational cost,the semianalytical model can reproduce the results obtained from MD simulations and match well with the results obtained from ab initio calculations.From the radius and RBM frequency results,it is shown that the simple rolling model is inappropriate in determining the equilibrium configuration of CNTs, especially for nanotubes with small radius.While the RBM frequency results obtained from the semi-analytical approach match reasonably well the ab initio results,differences are observed for CNTs with radius smaller than 2.6 Å.The discrepancy is due to the different underlying physical models of the two approaches.As the semi-analytical approach is independent of the potential energy functions,more accurate results may be obtained with other improved potential energy functions.

Acknowledgments The project was supported by the National Science Foundation(Grant CBET-0955096).

Appendix 1:Bond angle calculation

We obtain

Fig.A1 Bond angle calculation

Recalling Eq.(2),we have

Substituting Eq.(A.3)with hj=rjsinαjand lj=rjcosαjinto Eq.(A.2),we have

Appendix 2:REBO potential and its derivatives

The general form of the REBO potential energy is given by [32]

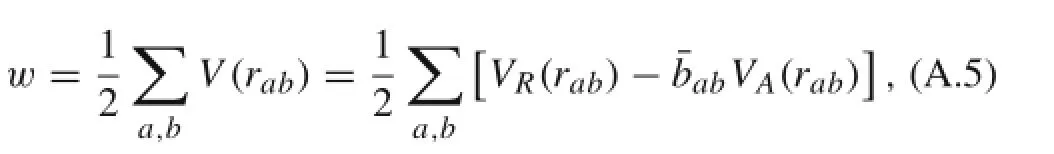
where VR(rab)and VA(rab)are repulsive and attractive energy between atom a and atom b,respectively.is the multi-body coupling modification term:In this work,due to the C2-axis rotational symmetry,bab=bba.Then the potential energy of a unit cell containing only one atom can be expressed using the bond indexes as

where j=1,2,3 are the indexes of three bonds surrounding an atom.The terms in Eq.(A.6)are given by[32]

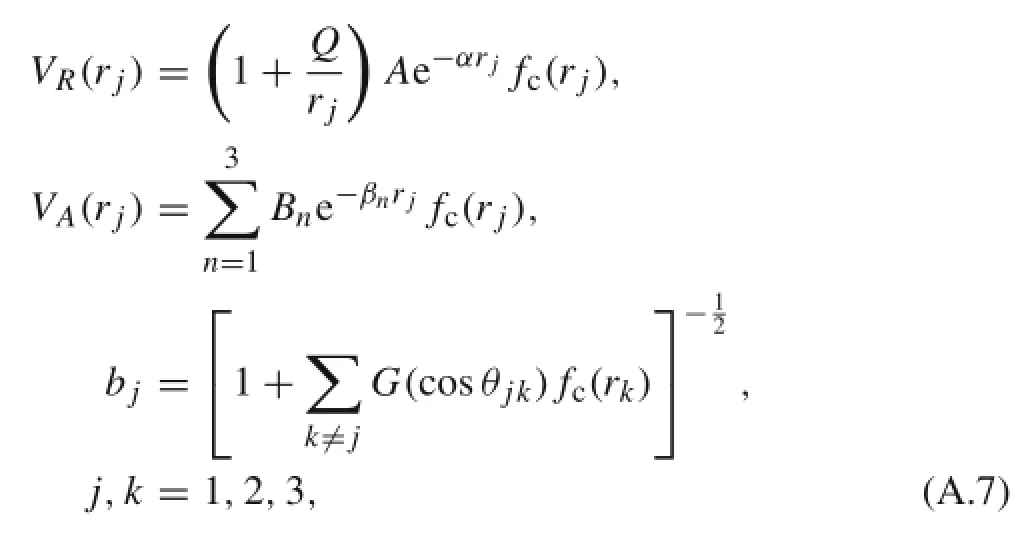
whereθjkis the angle between bond j and bond k.The cutoff function fc(r)is defined as

and G(cosθjk)is an empirical 6-order spline function.For C–C bonds,G(cosθ)is given by[37]

The constant parameters Q,A,α,Bn,βn,R1,and R2are listed in Table A1[23].

Table A1 Parameters for VRand VA

where

References

1.Baughman,R.H.,Zakhidov,A.A.,de Heer,W.A.:Carbon nanotubes-the route toward applications.Science 297,787–792 (2002)

2.Treacy,M.M.J.,Ebbesen,T.W.,Gibson,J.M.:Exceptionally high young’s modulus observed for individual carbon nanotubes.Nature 381,678–680(1996)

3.Li,C.,Chou,T.W.:A structural mechanics approach for the analysis of carbon nanotubes.Int.J.Solids Struct.40,2487–2499(2003)

4.Odegard,G.M.,Gates,T.S.,Nicholson,L.M.:Equivalent-continuum modeling of nano-structured materials.Compos.Sci. Technol.62,1869–1880(2002)

5.Tserpes,K.I.,Papanikos,P.:Finite element modeling of singlewalled carbon nanotubes.Compos.Part B 36,468–477(2005)

6.Yakobson,B.I.,Brabec,C.J.,Bernholc,J.:Nanomechanics of carbon tubes:instabilities beyond linear response.Phys.Rev.Lett.76, 2511(1996)

7.Pantano,A.,Parks,D.M.,Boyce,M.C.:Mechanics of deformation of single-and multi-wall carbon nanotubes.J.Mech.Phys.Solids 52,789–821(2004)

8.Hu,Y.G.,Liew,K.M.,Wang,Q.,et al.:Nonlocal shell model for elastic wave propagation in single-and double-walled carbon nanotubes.J.Mech.Phys.Solids 56,3475–3485(2008)

9.Jefferson,Z.,Zheng,Q.S.,Wang,L.F.,et al.:Mechanical properties of single-walled carbon nanotube bundles as bulk materials.J. Mech.Phys.Solids 53,123–142(2005)

10.Wang,Q.:Wave propagation in carbon nanotubes via nonlocal continuum mechanics.J.Appl.Phys.98,124301(2005)

11.Liu,J.Z.,Zheng,Q.,Jiang,Q.:Effect of a rippling mode on resonances of carbon nanotubes.Phys.Rev.Lett.86,4843(2001)

12.Qian,D.,Wagner,G.J.,Liu,W.K.,et al.:Mechanics of carbon nanotubes.Appl.Mech.Rev.55,495–533(2002)

13.Sánchez-Portal,D.,Artacho,E.,Soler,J.M.,et al.:Ab initio structural,elastic,and vibrational properties of carbon nanotubes.Phys. Rev.B 59,12678(1999)

14.Vaccarini,L.,Goze,C.,Henrard,L.,et al.:Mechanical and electronic properties of carbon and boron-nitride nanotubes.Carbon 38,1681–1690(2000)

15.Chang,T.,Gao,H.:Size-dependent elastic properties of a singlewalled carbon nanotube via a molecular mechanics model.J.Mech. Phys.Solids 51,1059–1074(2003)

16.Wang,L.,Zheng,Q.,Liu,J.Z.,et al.:Size dependence of the thinshell model for carbon nanotubes.Phys.Rev.Lett.95,105501 (2005)

17.Wang,Q.:Effective in-plane stiffness and bending rigidity of armchair and zigzag carbon nanotubes.Int.J.Solids Struct.41, 5451–5461(2004)

18.Huang,Y.,Wu,J.,Hwang,K.C.:Thickness of graphene and singlewall carbon nanotubes.Phys.Rev.B 74,245413(2006)

19.Ghavanloo,E.,Ahmad Fazelzadeh,S.,Rafii-Tabar,H.:Analysis of radial breathing-mode of nanostructures with various morphologies:a critical review.Int.Mater.Rev.60,312–329(2015)

20.Kürti,J.,Kresse,G.,Kuzmany,H.:First-principles calculations of the radial breathing mode of single-wall carbon nanotubes.Phys. Rev.B 58,R8869(1998)

21.Saito,R.,Hofmann,M.,Dresselhaus,G.,et al.:Raman spectroscopy of graphene and carbon nanotubes.Adv.Phys.60, 413–550(2011)

22.Kürti,J.,Zólyomi,V.,Kertesz,M.,et al.:The geometry and the radial breathing mode of carbon nanotubes:beyond the ideal behaviour.New J.Phys.5,125(2003)

23.Jiang,H.,Zhang,P.,Liu,B.,et al.:The effect of nanotube radius on the constitutive model for carbon nanotubes.Comput.Mater. Sci.28,429–442(2003)

24.Popov,V.N.:Curvature effects on the structural,electronic and optical properties of isolated single-walled carbon nanotubes within a symmetry-adapted non-orthogonal tight-binding model.New J. Phys.6,17(2004)

25.Popov,V.N.,Lambin,P.:Radius and chirality dependence of the radial breathing mode and the g-band phonon modes of single-walled carbon nanotubes.Phys.Rev.B 73,085407(2006)

26.Saito,R.,Dresselhaus,G.,Dresselhaus,M.S.,etal.:Physical Properties of Carbon Nanotubes,4.World Scientific,Singapore(1998)

27.Zimmermann,J.,Pavone,P.,Cuniberti,G.:Vibrational modes and low-temperature thermal properties of graphene and carbon nanotubes:minimal force-constant model.Phys.Rev.B 78,045410 (2008)

28.Lawler,H.M.,Areshkin,D.,Mintmire,J.W.,et al.:Radialbreathing mode frequencies for single-walled carbon nanotubes of arbitrary chirality:first-principles calculations.Phys.Rev.B 72, 233403(2005)

29.Xiao,Y.,Li,Z.M.,Yan,X.H.,et al.:Curvature effect on the radial breathing modes of single-walled carbon nanotubes.Phys.Rev.B 71,233405(2005)

30.Chang,T.:Explicit solution of the radial breathing mode frequency of single-walled carbon nanotubes.Acta Mech.Sin.23,159–162 (2007)

31.Cheng,H.C.,Liu,Y.L.,Wu,C.H.,et al.:On radial breathing vibration of carbon nanotubes.Comput.Methods Appl.Mech.Eng.199, 2820–2827(2010)

32.Brenner,D.W.,Shenderova,O.A.,Harrison,J.A.,et al.:A secondgeneration reactive empirical bond order(rebo)potential energy expression for hydrocarbons.J.Phys.14,783(2002)

33.Tersoff,J.:Empirical interatomic potential for carbon,with applications to amorphous carbon.Phys.Rev.Lett.61,2879(1988)

34.Stillinger,F.H.,Weber,T.A.:Computer simulation of local order in condensed phases of silicon.Phys.Rev.B 31,5262(1985)

35.Fletcher,R.,Reeves,C.M.:Function minimization by conjugate gradients.Comput.J.7,149–154(1964)

36.Powell,M.J.D.:An efficient method for finding the minimum of a function of several variables without calculating derivatives.Comput.J.7,155–162(1964)

37.Wu,J.,Zhang,Z.,Liu,B.,et al.:Numerical analyses for the atomistic-based shell theory of carbon nanotubes.Int.J.Plast.25, 1879–1887(2009)

✉G.Li gli@clemson.edu

1Department of Mechanical Engineering,Clemson University, Clemson,SC 29631,USA

19 March 2016/Revised:20 April 2016/Accepted:27 April 2016/Published online:10 September 2016