轴辐式物流网络模型的参数算法

罗玉宏，张 琳

（上海对外经贸大学统计与信息学院，上海201620）

轴辐式物流网络模型的参数算法

罗玉宏，张 琳

（上海对外经贸大学统计与信息学院，上海201620）

为了及时高效地为企业寻找到最优的轴辐式物流网络，将经典运输问题的网络模型抽象成平面图的形式，将轴辐式网络优化问题转化为构造一棵总运输费用最小的共享树问题。借助参数算法理论，提出一种启发式算法，首先通过构造一棵包括所有起讫节点的最小连通生成树，然后依次向树中添加能减少共享树总权值的非终端节点，最终生成一棵节点总数不超过参数k的最小共享树。实验表明，该算法具有较好的准确性和更高的时间效率，适用于网络规模大、终端配送节点较少的物流网络。

运输网络；规模效应；共享树；参数算法

1　轴辐式物流网络研究现状

物流网络是一个复杂的网络系统，网络优化的核心是确定合适的物流节点位置、规模和数量，选择合适的连接线路及运输方式，使物流网络在满足服务要求的基础上总的运输成本最低。轴辐式物流网络是以一个或多个枢纽节点为轴 (hub)，环绕在这些节点周围的非枢纽节点为辐 (spoke)，网络中通过线路 (link) 连接轴辐节点，实现货物传递的一种网络结构。轴辐式物流网络便于集中运输，达到规模经济的效益，对批次多、批量小、货点分散的快速物流网络而言尤其有效，对解决国内物流成本居高不下的问题能起到积极的作用，是未来物流网络的发展方向。

轴辐式网络的概念最早是由 Gordon 和 Neufville提出[1]，O’KELLY M E[2-3]首次提出轴辐式网络枢纽选址问题，指出枢纽选址问题是一种 NP 问题。当网络节点扩大到一定规模时，受轴辐式物流网络模型复杂性的限制，大多数精确算法在求解轴辐式物流网络的现实问题中很难获得最优解，算法的效率和精度一直是构建轴辐式网络面临的问题。许多学者对轴辐式物流网络算法进行研究，TOPCUOGLU H 等[4]提出用遗传算法求解轴辐式物流网络模型，该算法能大幅节省计算所消耗的时间；PIRKUL H 等[5]设计基于拉格朗日松弛的启发式算法，能够控制在 5 min 之内求解轴辐式物流网络模型；SUNG C S 等[6]研究混合轴辐式网络，采用二次上升、二次调整的方法确定并缩小解空间，直到得出满意解；MENG Q 等[7]为多式联运的轴辐式物流网络模型开发基于遗传算法的混合启发式算法，具有快速、精确的特点。

国内对轴辐式物流网络研究起步较晚。倪玲霖等[8]分析研究轴辐式物流网络和全连通物流网络的特点，得出轴辐式物流网络在一般情况下效果要优于全连通物流网络；崔小燕等[9]研究无容量限制的单分配轴辐式物流网络，提出基于蚁群算法的启发式求解算法；王玉勤[10]利用主成分分析法对贵州省各个城市的物流能力进行评价，并借助城市空间引力模型构建贵州省轴辐式物流网络；张银花[11]研究基于服务能力的轴辐式物流网络设计；刘沛[12]研究具有专线的混合轴辐式物流网络规划问题，并采用遗传算法进行求解；刘四辈等[13]研究考虑时间窗的轴辐式物流网络问题，并设计启发式算法用来求解；卫婵婵等[14]研究基于多式联运的轴辐式物流网络，各枢纽之间采用分段函数来表示规模运输的折扣系数，并且采用禁忌搜索算法进行求解。

构建轴辐式物流网络是一个 NP 难问题，随着网络规模的增大，上述算法在时间性能和准确度方面都有较大程度的下降，影响实际的应用。参数理论是近年发展起来的解决该难题的一项有效技术。参数理论的研究最初来源于观察到很多计算问题都与一个取值范围很小的重要参数相联系，利用参数的性质可以在一定程度上加速计算。将物流网络模型抽象成平面图的形式，将轴辐式网络优化问题转化为构造一棵最小共享树问题，然后借助参数算法理论，提出一种启发式优化算法。

2　轴辐式物流网络模型

2.1问题提出

定义运输起点 (起始节点) Ai，i = 1，2，…，p，其中 p 为起始节点个数。需要从 Ai运输的货物量为 ai，运往目的地 (终端节点) Bj的货物量为 bj， j = 1，2，…，q，其中 q 为终端节点个数，。问题是如何最快构造轴辐式物流网络，使总运输费用最低。

2.2模型假设

（1）构成的轴辐式物流网络中至少包含 m 个节点，其中 m = p + q。

（2）起始节点与终端节点之间的运输没有容量和时间限制，运输费用包括：非中心节点到中心枢纽的运输成本；中心枢纽之间的规模运输成本；中心枢纽站到目标节点的运输成本。

（3）采用单一枢纽指派，即网络中的非中心节点仅和一个中心枢纽连接。

（4）采用多枢纽轴辐式物流网络，即允许存在多个中心枢纽，非中心枢纽依靠一定规则分配给这些中心枢纽，与不同中心枢纽连接的非中心节点通过枢纽间的运输与再转运实现货物运输。

（5）采用多式联运，即在运输货物的过程中，经过 2 种或 2 种以上的运输方式 (如铁路、公路、航空、水运等)，将货物从起始节点运送到终端节点。几种不同的运输方式都有各自不同的成本费率；一般情况下，铁路的单位运输成本费率最低，而航空的单位运输成本最高[15]。

（6）中心枢纽之间运输具有规模效应，即通过扩大规模的方式来减少成本，并带来收益的提高。规模效应的折扣系数随着货物流量的变化而变化。

2.3模型构建

构建一个无向图G = (V，E)，V 为节点集合，V = {A，R，B}。其中，A 为起始节点集，A = {A1，A2，…，Ap}；B 为终端节点集，B = {B1，B2，…，Bq}；R 为中转节点集，R = {R1，R2，…，Rn-p-q}，n 为集合 V 中节点个数； E 为链路 (边) 集合，E = {eij| i，j ∈ V}。

共享树是以源节点为树根节点，以多个枢纽节点为轴节点，以非枢纽节点为辐节点，按照总运输费用最小建立的树型结构。在共享树中，任一运输源节点可以通过共享树向树中指定的多个目标节点发送货物。以 s 为树根节点，其他黑色节点为轴节点，白色节点为辐节点，构建以 s 为源节点的共享树如图1所示。

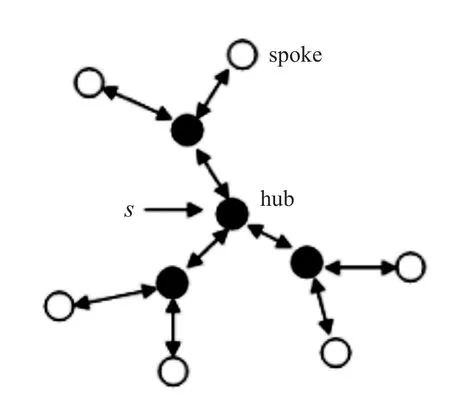
图1　以 s 为源节点的共享树

基于源节点 s 的共享树 T 中节点 i 的运输费用可表示为

式中：Vi为辐节点 i 单位质量货物联运的中转费用，元/kg；Eij为单位质量货物从节点 i 运输到其邻节点j 所产生的费用，元/kg；λij为从节点 i 到其邻节点 j 运输货物的量，kg；Eih为单位质量货物从轴节点 i 运输到其邻节点 h 所产生的费用，元/kg；λih为从轴节点 i 到其邻节点 h 运输货物的量，kg；δ 为节点 i 邻节点的个数；δ1为轴节点 i 邻居轴节点的个数；δ2为轴节点 i 邻居辐节点的个数；d为轴节点之间规模运输时的运费折扣系数。

货物运输的总费用，即共享树 T的总权值可表示为

因此，上述运输问题转换为求最小共享树问题，这类问题属于 NP 难问题。拟采用参数算法理论求解。

3　轴辐式物流网络的参数算法

参数算法是基于参数复杂度理论设计的一类算法，其运行时间复杂度具有特殊的形式。如果某个算法的时间复杂度为 f (k) nc，则称该算法为固定参数算法。其中，k 是问题的参数，n 是问题输入规模的大小，c 是一个独立于 k 和 n 的常数，f (k) 是以 k 为自变量的可计算函数。在参数算法中，用参数理论来求解 NP 难问题，需要将问题转换为参数算法中连接的节点覆盖问题，并提出解决该问题的启发式算法。

3.1参数问题转换

第一，输入一个给定的无向连通图G (V，E)及一个正整数 k，k≥m = p + q。第二，问题转换：图G 是否存在一个数量不超过 k 个节点的覆盖 G' ⊂ G，G' 是包含 m 个指定节点的连通的树，并且树的总权值最小。为方便参数问题的求解，在无向连通图G 中，共享树 T 有 m 个终端节点和一些非终端节点，令 σ = max (Eij) / min (Eij)，所以共享树本质上是一棵 Steiner 树，具有如下性质：①如果终端节点导出的子图为连通图，对 T 中任一非终端节点 v，节点 v 的度 d (v)≥[σ / (σ－1)]。②如果终端节点导出子图为连通图，对 T 中非终端节点的个数 l≤[m (σ－1)]；如果终端节点导出子图是不连通的，非终端节点的个数 l≤[m (σ－1)] + σ |V1|，V1是让终端节点导出子图连通的非终端节点的集合。③在连接的节点覆盖问题中，最小共享树 T 的节点数 k≤m + l。

3.2启发式算法

3.2.1算法描述

（1）采用分布式算法，直接构造一棵包含 m 个终端节点的最小连通生成树 T (非终端节点尽可能地少，只为了维持树的连通性，添加必不可少的非终端节点)。对生成树 T 中所有非终端节点的叶子节点剪枝，作为备选节点存放在集合 B 中。为方便计算，对树中任一节点 i，增加选路表和费用信息表。选路表由三元组 (vd，vn，Cmin) 构成，其中vd为目的节点，vn为由节点 i 运输货物到达 vd节点要选择的邻居节点，Cmin为由节点 i 运送单位质量货物到达 vd的最小费用。费用信息表由四元组 (j，λij，vi，d)构成，分别用来存放节点 i 到其任一邻居节点j 的货物运输量λij、联运费用 vi和折扣率 d。处理过程如下：①任一节点计算到邻居节点最小费用 Cmin，建立选路表，然后将选路表告诉它所有的邻居节点；②任一节点收到邻居节点的选路信息后，对其选路表进行添加、删除或修改，并将新的选路信息告诉所有的邻居节点；③重复步骤②，直到所有节点不再有选路信息的更新；④所有的运输起点将要运送货物的数量和目的地等信息告诉它的邻节点 (假设为 i)；⑤邻节点 i 收到该信息后，根据选路表的信息，选择不同的转发邻节点 (假设为j)，分别计算λij，vi，d，将这些信息存放在费用信息表中，然后将要通过j 运送货物的数量和目的地等信息转发给j；⑥重复步骤⑤，直到所有的信息都传递到目的节点。

（2）对生成树 T 进行优化，减少生成树 T 的总权值。按轮对生成树 T 进行优化，每一轮优化过程都从生成树根节点 s 开始。①按照固定的次序依次遍历树 T 的每一个节点，如果一轮遍历结束后，树的结构没有发生变化，则终止优化。②当遍历经过节点 i 时，节点 i 的处理过程如图2所示。节点 i 的任一邻居节点 p ( p 不在节点 i 的子树中)，假设节点 i 更改其父节点 v 为节点 p，计算生成树费用的减少，记为 Gainv-＞p。当节点 i 更改父节点由 v 到 p 时，运输费用受到影响的节点是从节点 v 指向根节点的路径 (v-＞u) 和节点 p 指向根节点的路径(p-＞u)，节点 u 为节点 v 和 p 的共同祖先。分别运用公式 ⑴ 计算路径 i-v-u-p 中各个节点的费用变化情况，并汇总为 Gainv-＞p。节点 i 选择最大的正的Gainv-＞p所在的 p 节点 (如果这样的点存在) 为新的父节点，节点 i 更改父节点后，向邻居节点通告新的选路信息并更新自身的费用信息表。生成树中其他节点收到新的信息后，更新自身的选路表和费用信息表。遍历下一个节点。③删除可能存在的非终端叶子节点，并且更新生成树 T 的信息。显然，这时树 T 中尽可能只包含所有起始节点和终端节点，并且 |T |≤k ( |T | 表示树 T 中节点的个数)，总费用接近最优。

图2　节点 i 更改父节点由 v 到 p

（3）用参数 k 来控制生成树 T 的规模，向树 T中逐步加入符合优化条件的非终端节点，寻找总费用趋向最优的共享树。①如果 |T | ＜ k，重复以下步骤②-⑤；②依次从备选集 B 中取出一个节点 v (v 必须是树 T 中节点的邻居节点)；③节点 v 在它的邻居节点中寻找属于生成树 T 中的节点 u，使节点 v 连接到节点 u 后距离最小；④对节点 v 在生成树中的任一邻居节点j (节点 u 除外) 进行是否更改父节点判断，如果j 选择 v 作为其父节点，则证明节点 v 的加入将减少生成树的总费用，那么：将 v 连接到节点 u，将 |T | 加 1；将 j 连接到节点 v；节点 v，j 更新各自的选路表和费用信息表，向邻居节点通告新的选路信息；生成树中其他节点收到新的信息后，更新自身的选路表和费用信息表；删除 T 中存在的非终端叶子节点，每删除 1 个，进行|T |减 1 的操作，更新生成树 T 的信息。⑤如果备选集 B 中符合条件的任一节点加入，生成树中不再改变，终止上述操作。

3.2.2算法性能分析

第一阶段构造初始的生成树 T 和对生成树 T 进行剪枝，时间复杂度为 O (nlogn)； 第二阶段中优化初始的生成树 T 的过程中，时间复杂度为O (kδT)，δT是树的度；第三阶段生成树优化过程中，最多会分析 kδG个结点是否改变连接节点的判断，δG是图G 的度，时间复杂度为 O (kδGδT)。因此，启发式算法总的时间复杂度为 O (nlogn + kδGδT)，参数 k 很好地控制了算法的规模。当 k 值相对 n 较小时，算法具有明显的性能优势；当 k 值增大时，算法的性能会有所下降，当 k→n，算法的时间性能达到O (nlogn + nδG)。

4　案例分析

4.1基础数据

物流网络规模由全国 100 个大中城市 (以 2014年全国 GDP 排名前 100 名的城市为例) 构成。联运仅考虑常用的铁路和公路 2 种情况，各城市之间的铁路和公路运输距离数据分别来自列车时刻网[16]和长途吧网[17]。

铁路运输费用按照《国家发展改革委关于调整铁路货运价格进一步完善价格形成机制的通知》[18]执行。案例中采用零担货物方式，其中，铁路零担以 10 kg 为单位，不足 10 kg 按照 10 kg 计算，铁路运输费用公式为 Eij= 0.280 + 0.001 55×dij。其中，Eij为从节点 i 到节点j 采用铁路运输 10 kg 货物的费用，元；dij为节点 i 和j 之间的距离，km；0.280 为 10 kg 货运起运价，元；0.001 55 为每 1 km每 10 kg 货运的价格，元。

公路零担以 1 kg 为单位，普通货物的公路运输费用公式为 Eij= 0.000 3×dij。其中，Eij为从节点 i 到节点j 采用公路零担运输 1 kg 普通货物的费用，元；0.000 3 为每 1 km 每 1 kg 普通货物全国货运平均价格，元。

记规模运输的折扣系数为 d = 1－λij/ 100 000 (假设计费重量超过 1 000 kg 才开始使用折扣系数，最大折扣系数不小于 0.8)；铁路和公路间转运的费用Vi= 0.011 元/kg；货物运送的起讫点随机产生，每个起点的货运量在 [500，5 000] (kg) 之间随机产生。

4.2案例分析

实验随机货物运送起点 ( p) 和目的地 (q) 的总和m 取值为 (10，20，…，100)，实验平台采用的主要配置为 Windows 7 操作系统，intel® CoreTMi3 CPU M380@2.53GHz， 2GB 内存，使用 C++ 编写算法并使用 GCC 4.8.5 进行编译。分别模拟 100次，取 95% 的置信区间，实验结果如下。

（1）算法准确性比较。将启发式算法所生成的共享树的总运输费用，与通过枚举法 (精确算法) 获得的运算结果进行比较，二者费用的总比值用准确度表示，如表1 所示。

表1　启发式算法和精确算法总运输费用及比值

结果显示启发式算法的准确性随着 m 的增大而得到提高，当 m 接近 100 时，准确度达到 104% 左右；当 m = 10 时，准确度最差，达到 106.2%。总体上算法具有较高的准确性。

（2） 算法运行效率比较。记算法的运行效率为启发式算法和精确算法运行时间的比值，启发式算法和精确算法的运行时间如表2 所示。

表2　启发式算法和精确算法运行时间及比值

可以看出，启发式算法具有较好的运行效率，运行时间只有枚举法的 1%～2% 之间。随着 m 的增大，二者运行的时间都在增大，但是启发式算法增大的幅度更大一些。实验表明，启发式算法在 m 远小于网络规模 n 时，更加能体现出算法的时间性能。

5　结束语

参数理论是近年来发展起来的解决 NP 难问题的一项有效技术，利用参数的性质可以在一定程度上降低问题的规模，加速计算。借助参数算法理论，运用启发式算法构造了一棵节点总数不超过参数 k 的最小共享树，用非常少的时间对轴辐式物流网络进行了优化，相对传统的算法具有较好的准确性和更高的时间效率，特别适应于网络规模大，终端配送节点较少的物流网络。今后的研究将结合航运、空运，综合考虑最短时限运输问题，带时间窗的路径优化问题、带车容量限制的路径优化问题等，使算法更趋向于实际应用。

[1] 朱宇清. 多式联运轴辐式物流网络的设计优化研究[D]. 西安：长安大学，2013.

[2] O’KELLY M E. The Location of Interacting Hub Facilities[J]. Transportation Science，1986，20(2)：92-106.

[3] O’KELLY M E. A Quadratic Integer Program for the Location of Interacting Hub Facilities[J]. Euro Journal of Operational Research，1987，32(3)：393-404.

[4] TOPCUOGLU H，CORUTA F，ERMIS M，et al. Solving the Uncapacitated Hub Location Problem Using Genetic Algorithms[J]. Computer&Operations Research，2005，32(4)：967-984.

[5] PIRKUL H，SCHILLING D A. An Efficient Procedure for Designing Single Allocation Hub and Spoke Systems[J]. Management Science，1998，44(12)：235-242.

[6] SUNG C S，JIM H W. Dual-Based Approach for a Hub Network Design Problem under Non-Restrictive Policy[J]. European Journal of Operational Research，2001，132(1)：88-105.

[7] MENG Q，WANG X C. Intemodal Hub-and-Spoke Network Design：Incorporating Multiple Stakeholders and Multi-Type Containers[J]. Transportation Research Part B，2011，45(4)：724-742.

[8] 倪玲霖，史 峰，方晓平，等. 全连通快递网络与轴辐快递网络的比较[J]. 系统工程，2009，27(12)：45-50.

NI Ling-lin，SHI Feng，FANG Xiao-ping，et al. Comparative Study on Fully-Connected and Hub-and-Spoke Express Operational Networks[J]. Systems Engineering，2009，27(12)：45-50.

[9] 崔小燕，李旭宏，毛海军，等. 无容量约束单分配轴-辐式物流网络设计[J]. 交通运输系统工程与信息，2010，10(5)：175-181.

CUI Xiao-yan，LI Xu-hong，MAO Hai-jun，et al. Design of Uncapacitated Hub-and-Spoke Logistics Networks with Single Allocation[J]. Journal of Transportation Systems Engineering and Information Technology，2010，10(5)：175-181.

[10] 王玉勤. 贵州省轴辐式物流网络构建研究[J]. 铁道运输与经济，2015，37(12)：41-46.

WANG Yu-qin. Study on Establishment of Hub-and-Spoke Logistic Network in Guizhou Province[J]. Railway Transport and Economy，2015，37(12)：41-46.

[11] 张银花. 基于服务能力的轴辐式物流网络构建研究[D]. 北京：北京交通大学，2012.

[12] 刘 沛. 轴辐式快递货运网络规划研究[D]. 济南：山东大学，2007.

[13] 刘四辈，胡大伟. 带时间窗的公路快速货运轴辐式网络设计研究[D]. 西安：长安大学，2011.

[14] 卫婵婵，胡大伟. 多式联运枢纽网络的优化设计研究[D].西安：长安大学，2012.

[15] 李珍萍，周文峰. 物流配送中心选址与路径优化问题—建模与求解[M]. 北京：机械工业出版社，2014.

[16] 列车时刻网. 距离[EB/OL]. (2009-01-01) [2015-07-01]. http://juli.liecheshike.com/.

[17] 长途吧网. 距离[EB/OL]. (2009-01-01)[2015-07-01]. http://www.changtu8.com/.

[18] 国家发展和改革委员会价格司. 关于调整铁路货运价格进一步完善价格形成机制的通知：发改价格[2015]183号[A/ OL]. (2015-01-29)[2015-07-01]. http://jgs.ndrc.gov.cn/ zcfg/201501/t20150130_662799.html.

责任编辑：王 静

The Parameterized Algorithm for Hub-and-Spoke Logistics Network

LUO Yu-hong，ZHANG Lin

(School of Statistics and Information, Shanghai University of International Business and Economics, Shanghai 201620, China)

In order to find the optimal hub-and-spoke logistics network in time for companies, the network model of classical transportation problem is abstracted into the planar graph, and the optimization problem of logistics network is transformed into the problem of constructing a minimum shared tree. Then, a heuristic approximation algorithm is proposed based on the theory of parameter algorithm. First, the algorithm builds a connected minimum spanning tree including all origin-destinations (OD), and then adds the non-OD node to the tree one by one, which can reduce the total weight of the spanning tree, and lastly generates a minimum shared tree with nodes no more than k, and k is a small parameter. Experimental results show that the algorithm uses parameter k to reduce the complexity of the problem and has good accuracy and time efficiency, especially adapted to the large logistic network with less OD.

Transportation Network; Economy of Scale; Shared Tree; Parameterized Algorithm

1003-1421(2016)11-0035-06

F259.27

A

10.16668/j.cnki.issn.1003-1421.2016.11.08

2016-04-05

上海市教委科研创新重点项目 (12ZS170)