基于容错理论无级变速器故障诊断分类

韩 玲, 卢延辉, 安 颖, 田丽媛

(1.长春工业大学 机电工程学院,吉林 长春 130021；2.吉林大学 汽车工程学院,吉林 长春 130022；3. 湖南大学 汽车工程学院,湖南 长沙 410000)



基于容错理论无级变速器故障诊断分类

韩 玲1, 卢延辉2, 安 颖3, 田丽媛1

(1.长春工业大学 机电工程学院,吉林 长春 130021；2.吉林大学 汽车工程学院,吉林 长春 130022；3. 湖南大学 汽车工程学院,湖南 长沙 410000)

为了实现无级变速器(CVT)在线故障诊断及分类需求,基于改进人工蜂群算法结合最小二乘向量机,提取无级变速器故障特征向量,建立夹紧力与速比故障预测模型,按照预测模型进行故障定位、分类辨识.针对从动油缸压力、速比、执行机构等故障的特征向量进行Matlab仿真,分析经容错控制分类后的故障特征向量仿真曲线变化趋势.通过容错控制在Matlab/Simulink中建立无级变速器硬件在环仿真动态模型.结果说明,采用该方法,无级变速器故障诊断经容错可继续工作概率达98.728%,满足无级变速器在线故障诊断可靠性及稳定性的需求.

无级变速器；主动容错；改进人工蜂群算法；故障诊断

容错分类是一种具有冗余能力的控制思想,其控制宗旨在于解决系统的故障诊断及容错两个关键问题,因此,容错理论研究对提高系统可靠性、安全性、有效性起着至关重要的作用.近年来,容错控制已应用到众多领域,特别是在汽车领域的“汽车ESP滑移率约束”、“汽车线性转向”、“汽车主动悬架”、“汽车电子机械制动执行系统”、“电动汽车电机驱动系统”[1-4]等研究中被广泛应用.本文基于容错理论对CVT进行在线故障诊断及故障辨识分类,提出用于故障诊断的多特征组分析方法.

通过对CVT夹紧力和速比控制系统中主要元件的传感器、执行装置、TCU进行故障检测与诊断,提取了整体与局部关键元件特征参数.考虑到夹紧力与速比系统的非线性特征,采用单一方法提取故障特征向量会对复杂耦合故障存在后续分类较难等问题[5-6].为了解决上述情况,提高故障分类识别的有效性和准确度,加快故障识别系统寻优的收敛速度,将容错分类中最小二乘向量机(least squares support vector machine,LSSVM)理论与现在最热门智能算法之一的改进人工蜂群算法(improved artificial bee colony,IABC)相结合[7-12],兼具比传统方法更好的优化能力.利用该方法针对CVT的特性建立故障预测模型,对获取的故障参数进行多次修正反馈,对多种状态下的信号参数进行迭代学习,提高了故障分类的辨识精度,解决了夹紧力控制系统和速比控制系统的故障分离、定位、归类.以力帆620国产CVT车型为研究对象,针对车辆实际行驶工况下CVT的油门开度、转速、转矩、油缸压力、目标夹紧力、目标速比等输入信号变化及功率匹配的情况,在IABC-LSSVM算法的基础上,对CVT传感器进行建模分析,利用容错控制理论在Matlab/Simulink中建立了CVT控制系统硬件在环仿真动态模型.

为了验证CVT产生故障时容错的控制效果,对比了速比控制系统和从动油缸压力控制系统出现故障后,在有、无容错控制下的表现形式.试验结果显示,在CVT出现故障后：未经容错控制,系统将无法正常工作,导致瘫痪；经容错控制,系统会在可接受的安全可靠性范畴内,以“跛行”状态完成任务.经Matlab仿真结果表明,利用改进后的算法对正则化参数和核函数参数进行优化后,CVT整个系统表现出了更好的鲁棒性.本文设计的容错故障分类模型具有较高的预测精度.

1 基于IABC-LSSVM改进算法表述

LSSVM的基本思想是在确保分类精度不变的前提下减少运算量,和传统的分类算法相比,LSSVM在防止训练过学习、运算速度结果精度等方面都有明显的优越性.在日积月累的工作学习经验中,LSSVM进行了诸多的变形和改进,以提高更有效的辨识分类度.本文在LSSVM模型多特征参数优化的基础上引入IABC算法.该算法是将免疫算法的记忆功能引入传统ABC算法中,通过原始对偶内点法求解非线性问题并保留最优秀片段,克服了故障向量寻优过程中优秀故障特征向量过早收敛、早熟、寻优速度较慢等缺陷.

LSSVM是一种支持向量机SVM的变形算法.该算法的训练通过下式完成：

(1)

式中:yk∈R，N为训练样本数，φ(xk)从原空间映射到高维特征空间的将非线性函数拟合问题转化为高维的线性函数拟合，C为边际系数，ξ为引入的松驰因子，b为常量.定义拉格朗日函数：

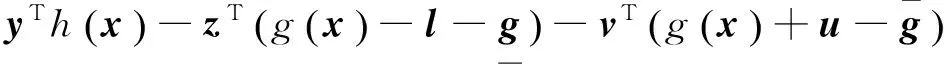
(2)

(3)

式中：y、z、v为拉格朗日乘子；μ为扰动因子；l、u为松驰变量，l>0,u>0,l∈Rn,u∈Rn,其中n为式(3)的不等式约束个数；y∈Rm,其中m为式(3)的约束个数；z∈Rn,v∈Rn且z>0,v<0.

根据KKT最优条件：

(4)

式中：e为n维列向量,

将式(4)进行泰勒级数展开,以矩阵形式可得修正方程：

(5)

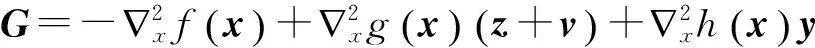
(6)

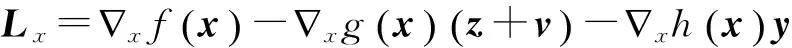
(7)

(8)

式中：αp、αd分别为原、对偶变量修正步长,

(9)

式中:γ为安全因子,原对偶内点法采用的收敛判据为ρ=lTz-uTv,收敛精度取ρ<10-6.若不满足上述条件,可以对扰动因子μ=σρ/(2n)进行修正,其中σ为向心参数,重新迭代进行收敛计算.

2 CVT故障诊断及容错控制策略

2.1 IABC-LSSVM对CVT预测模型的流程图

CVT故障参数提取的精确度是衡量故障诊断的一个综合指标,不仅反映了各零部件的工作状态,而且与整体CVT效率密不可分[13-16].影响CVT工作的因素有：夹紧力控制阀、速比控制阀、主、从带轮转速、从动带轮油压等.由于CVT故障提取预处理过程中存在诸多非线性因素：控制阀流量—压差特性、控制阀死区特性、供油压力饱和非线性、增益非线性、执行机构库仑摩擦引起的摩擦非线性等,因此难以建立精准的数学模型预测CVT在线故障.在综合比较CVT故障特征的基础上,本文选取夹紧力、夹紧力PWM驱动器电流、夹紧力执行机构、速比、速比PWM驱动器电流、速比执行机构作为预测模型输入,实际测量值为输出.利用提出的IABC-LSSVM算法建立CVT故障预测模型,对该模型进行可行性分析及验证.如图1所示为改进的人工蜂群算法与最小二乘向量机结合的算法流程图.

图1可以分为3大组成部分.首先通过CVT传感器对基本信息量进行采集；其次按照诊断初始化、IABC优化对样本归一化处理,极限循环对特征向量进行优化筛选；最后通过IABC-LSSVM完成故障诊断分类.

2.2 CVT电磁阀电流检测电路设计

CVT电控系统是压力闭环控制系统.它主要包括夹紧力控制系统和速比控制系统,两者采用单一液压回路,电控单元(TCU)依据预先设定好的控制策略确定当前行驶工况目标夹紧力和目标速比,将它们进一步转化为期望的主、从动油缸来控制油压并输出相应的控制信号,并对信号的反馈和控制进行修正.CVT夹紧力控制阀和速比控制阀均由PWM占空比控制,本文设计了PWM驱动电路,在驱动电路的基础上分析电流,从而实现电磁阀故障检测.如图2所示为CVT控制阀PWM驱动图.

在整个电路中,线圈、电源和开关管之间串联一个阻抗性分流器作为电流传感器.由于阻抗电流分流器的阻值较小,在分流器和电流表并联的时刻,根据分流器阻值和电流表内阻,可以通过电流表显示读出大电流数值.通过阻抗性分流器两端电压偏差计算阀线圈电流,完成电流检测.由于电流检测部分的运算放大器工作于高压端,必须选用高共轭抑制比的差分运算放大器,检测出感应电流提供一个更加准确的平均电流.复合晶体管工作于地端,TCU输出的逻辑电平可以直接驱动复合晶体管,更重要的作用是在所有可能短路的故障发生时,短路电流都要通过分流器起到检测短路的作用.

2.3 CVT故障预测模型建立

新增2个电流传感器于电控单元,用于检测夹紧力和速比控制阀线圈的过通电流,再结合主、从动带轮转速传感器和从动带轮油压传感器分别用于检测速比和油压,共5个传感器获取实时信号.电控单元的控制输出为速比控制器占空比和夹紧力控制器占空比.利用相应的输入、输出关系,建立以下6组预测模型.

夹紧力预测模型为

(10)

夹紧力PWM驱动器输出电流模型为

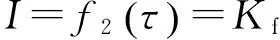
(11)

夹紧力执行机构模型为

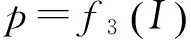
(12)

速比预测模型为

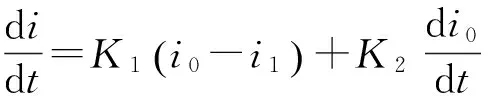
(13)

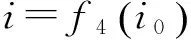
(14)

图1 改进的人工蜂群最小二乘向量机算法流程图Fig.1 IABC-LSSVM flow chart

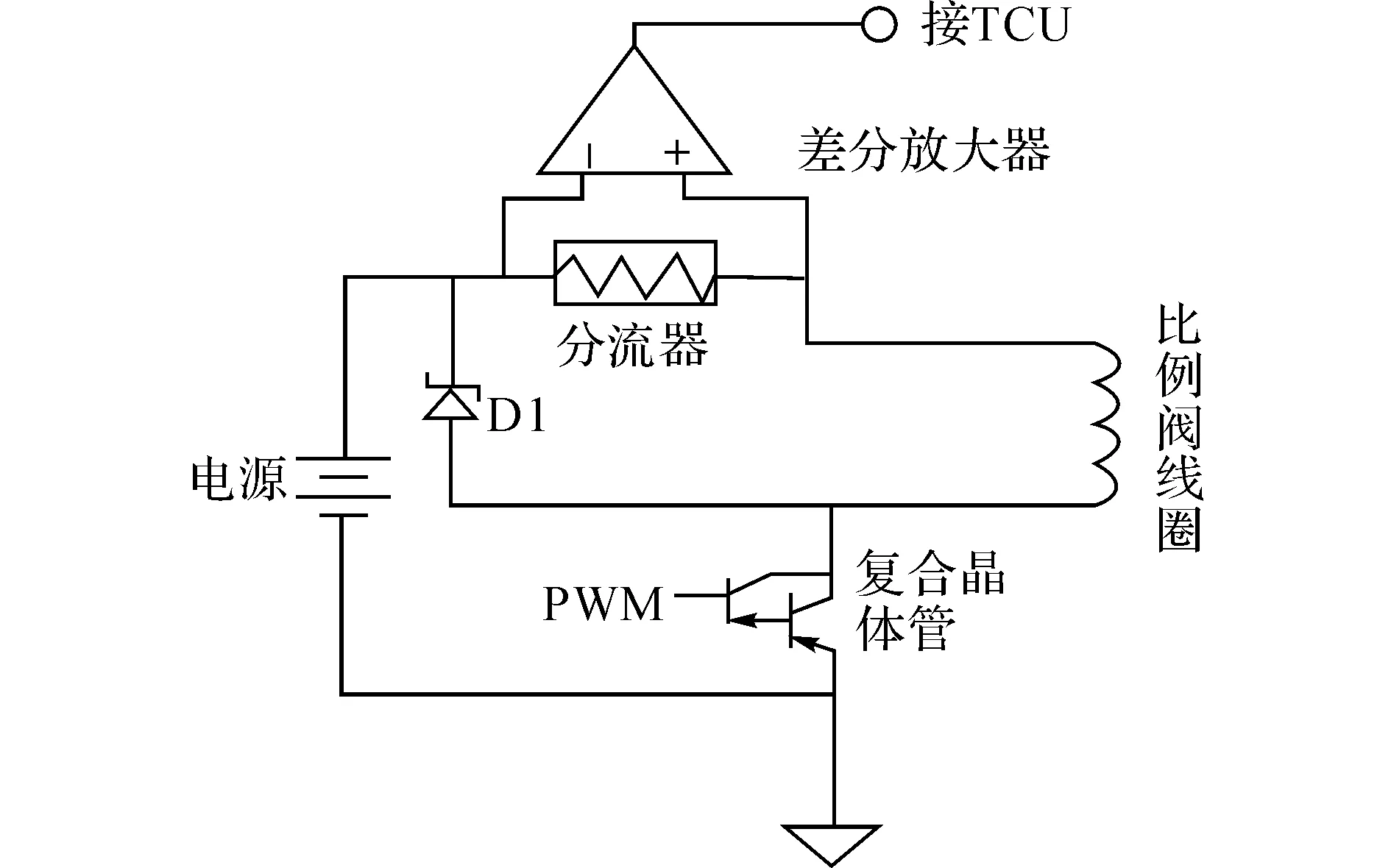
图2 CVT控制阀PWM驱动Fig.2 PWM driving of CVT control valve

速比PWM驱动器输出电流I模型为

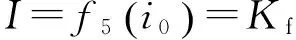
(15)

速比执行机构模型为

(16)

式中：Kf为PWM驱动器静态增益；τ为控制器输出信号占空比；I为PWM驱动器输出电流；p为从动带轮液压缸压力；K1为速比变化率低速区,K2为速比变化率高速区,比例系数由i决定.

连接上述模型比较预测模型与实际输出值,设残差值为r(k),当无故障和噪声时,残差一般应为零；在故障发生后,残差以确定性偏移量的形式出现.本文设残差r(k)偏离某数值为Δ,当系统无故障时,r(k)趋于某数值Δ.

(17)

式中：Δ为故障阈值.

基于以上6组预测模型的输出以及当前系统的实际输出,可以得到系统全局和局部的故障诊断结果.根据控制电流的实际检测值以及夹紧力和速比控制系统的工作原理,可以得到用于故障检测隔离与定位的故障逻辑表,如表1和2所示.当电流真实测量值超过夹紧力控制阀的额定电流时称为“故障”,即I≥Δn时，输出故障；电流真实测量值为零时称为“零值”；当电流真实测量值介于“零值”与“故障”之间时称为“正常”,即I<Δn时，输出正常.

表1 夹紧力控制系统故障隔离与定位逻辑

Tab.1 Fault isolation and location logic of clamping force control system

电流实测值全局模型驱动器模型执行机构模型可能的故障正常I<ΔI<ΔI<Δ无故障正常I≥Δ1I≥Δ1I<Δ1驱动器故障正常I<Δ2I≥Δ2I≥Δ2电流传感器故障正常I≥Δ3I<Δ3I≥Δ3控制阀故障液压缸故障或压力传感器故障过大I≥Δ4I≥Δ4I≥Δ4驱动电路或控制阀线圈短路零值I≥Δ5I≥Δ5I<Δ5驱动电路或控制阀线圈断路

表2 速比控制系统隔离与定位的故障逻辑表

Tab.2 Fault isolation and location logic of ratio control system

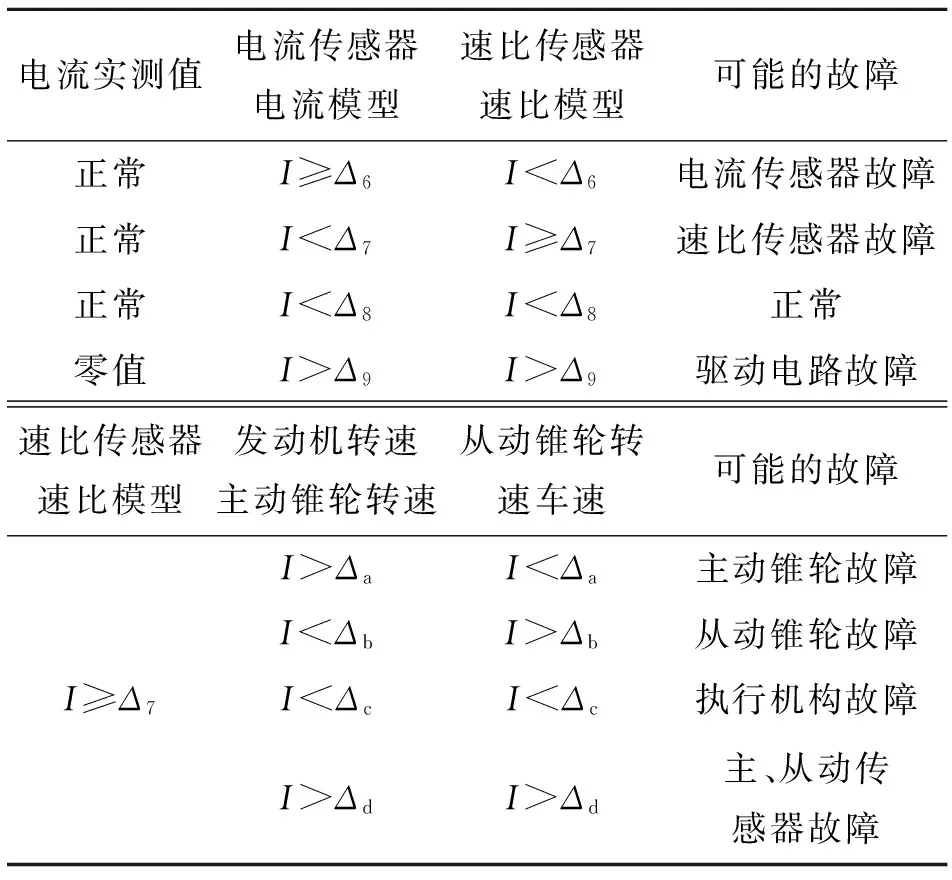
电流实测值电流传感器电流模型速比传感器速比模型可能的故障正常I≥Δ6I<Δ6电流传感器故障正常I<Δ7I≥Δ7速比传感器故障正常I<Δ8I<Δ8正常零值I>Δ9I>Δ9驱动电路故障速比传感器速比模型发动机转速主动锥轮转速从动锥轮转速车速可能的故障I≥Δ7I>ΔaI<Δa主动锥轮故障I<ΔbI>Δb从动锥轮故障I<ΔcI<Δc执行机构故障I>ΔdI>Δd主、从动传感器故障

2.4 基于IABC-LSSVM算法对CVT故障预测样本的提取及分类辨识测试

采用经过预处理的200组样本数据仿真,其中120组用于模型训练样本,其余80组用于模型测试样本.在Matlab2010b仿真环境下,利用IABC算法对扰动因子μ和向心参数σ进行优化修正,经过多次重复迭代试验,食物源数量设为30,食物源最大循环迭代次数为500,终止循环次数为50.

图3 电流特征向量Fig.3 Feature vectors of current

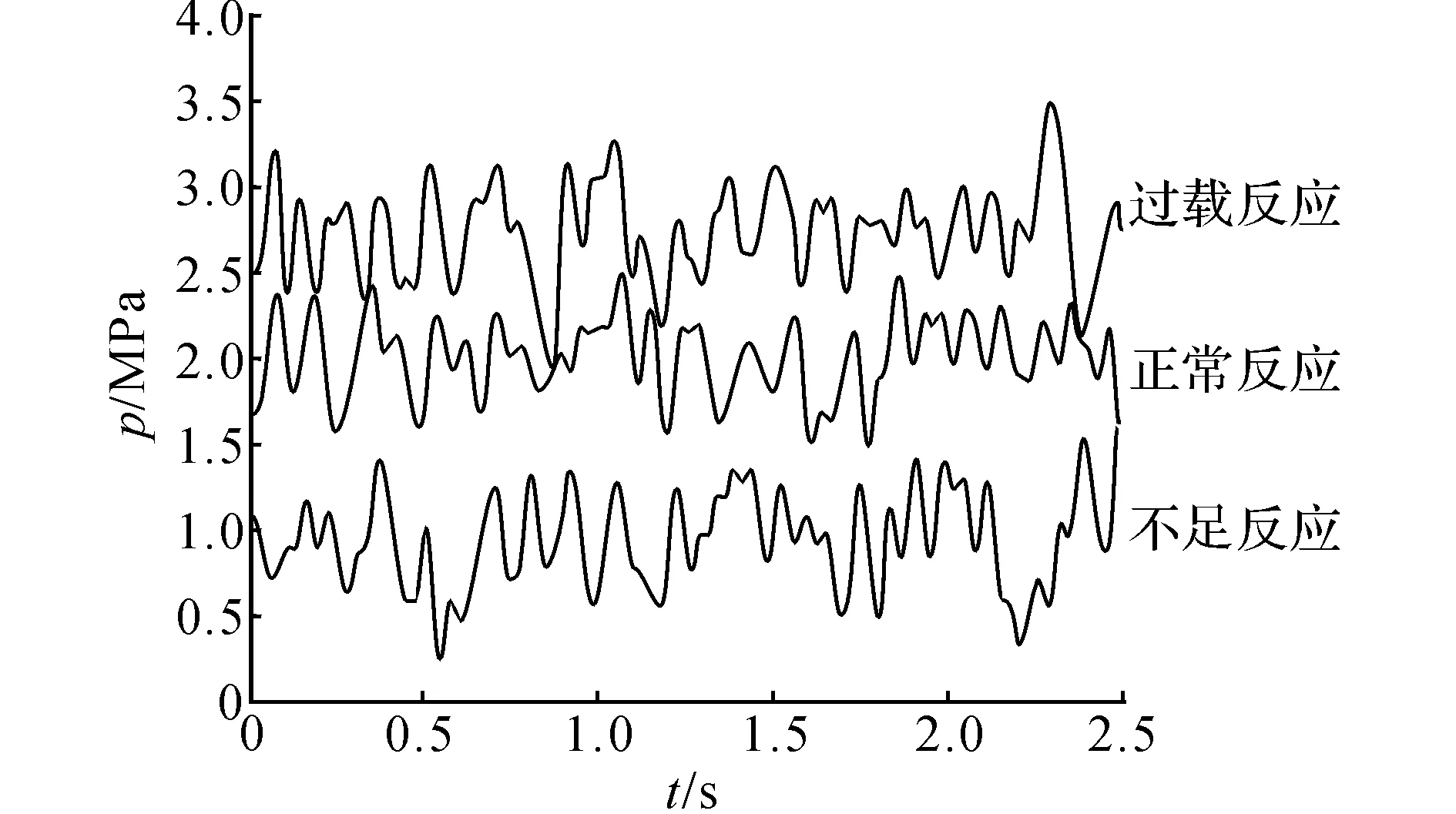
图4 从动油缸压力特征向量Fig.4 Feature vectors of second cylinder pressure

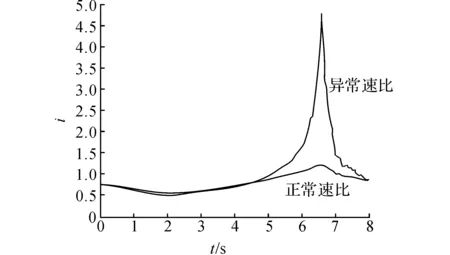
图5 速比特征向量Fig.5 Feature vectors of ratio

图6 执行机构特征向量Fig.6 Feature vectors of actuator

利用改进的LSSVM模型对测试样本预测,绘制电流特征样本、从动油缸压力特征样本、速比特征样本及执行机构特征样本部分曲线,如图3～ 6所示.图中，V为运行电压，T为周期.

为了证明IABC-LSSVM算法可提高预测模型的精度,建立无故障情况下特征向量的对比.对比结果可以看出,利用提取的参数方法可以有效地反映各特征向量分类情况.对CVT故障样本进行基础分类辨识测试,如图7所示.图中,X、Y轴分别代表各种故障的综合参数，没有固定单位.

图7 多种故障诊断分类Fig.7 Multiple faults diagnosis and classification

从图7可以看出,以复合故障为例,由于传感器获取的综合参数具有很高的相似度,传统的故障分析模式无法区分,利用提出的IABC-LSSVM的方法,在多模态特征信息分析中能够有效地辨识故障类型.

2.5 CVT容错控制策略

CVT容错控制策略的本质是分析多重状态故障特征向量,进行故障模式识别后的分类辨识.分类识别的主要过程包括故障参数特征分析提取、多重状态下分类训练以及相应的识别诊断等几大环节.CVT电控单元作为电液控制系统关键技术中的重要组成部分,它接收来自各种传感器和开关的输入信号,并通过运算分析,判断、预测CVT状态.在系统存在一定容错冗余度的情况下确定输出信号,诊断CVT可能发生的故障,从而有效地对CVT进行控制,使整个系统的鲁棒性更强.如图8所示为CVT诊断及容错策略流程图.

3 CVT容错仿真验证

由于CVT多特征提取模型的方法能够克服单一特征提取方法中所存在的缺陷,通过有效利用多特征信息的互补,为分类器组提供完备的诊断依据.对CVT容错仿真能力进行试验验证,建立硬件在环仿真模型,通过提取CVT故障注入后的参数,验证了仿真模型在容错控制的基础上对故障的有效识别.

3.1 无级变速器传动系统模型建立

在仿真模型中,以国产CVT车型为研究对象,主要参数见表3.由于CVT传动系统存在非线性的子系统,将传动系统进行合理化的精简,这样不仅便于转矩比动态模型的建立,而且对实用性没有任何影响,简化图如图9所示.

综合考虑驱动系统输出轴上相对的扭转刚度及阻尼,将输出轴简化为弹性系统.传动系统的动力学关系如下描述.

1) 发动机模型为

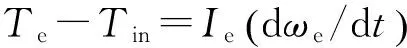
(18)

式中：Te为发动机输出转矩.

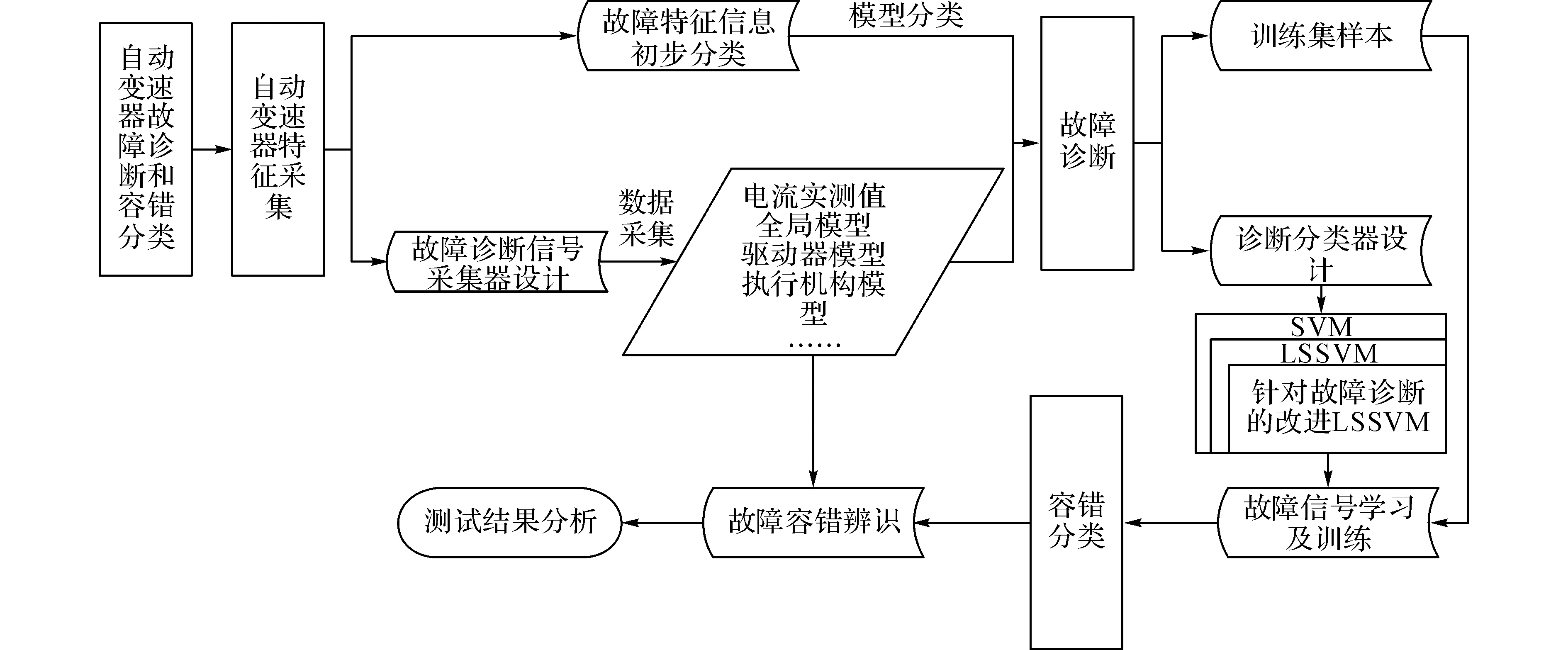
图8 CVT诊断及容错策略流程图Fig.8 Diagnosis and fault-tolerant strategy flow chart of CVT

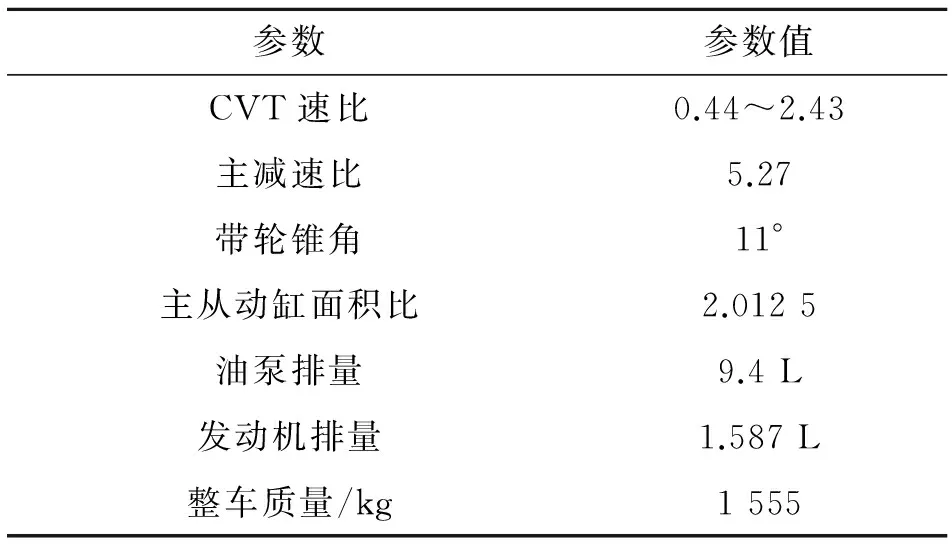
参数参数值CVT速比0.44～2.43主减速比5.27带轮锥角11°主从动缸面积比2.0125油泵排量9.4L发动机排量1.587L整车质量/kg1555

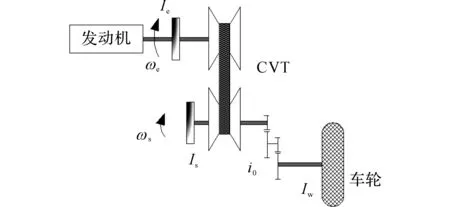
图9 CVT传动系统简化图Fig.9 Transmission system simplified diagram of CVT

2)CVT模型为

iCVTTin=

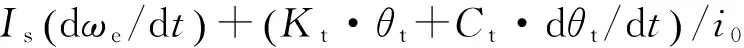
(19)

(20)

式中:Ie为发动机飞轮转动惯量,Is为从动带轮及主减速器在从动带轮上的等效转动惯量,Iv为驱动轴上等效转动惯量,iCVT为无级变速器传动比,i0为主减速器传动比,θt为驱动轴相对扭转角,Kt为相对扭转刚度,Ct为阻尼系数,Td为行驶中阻力矩.

3)驱动轴模型为

θt=θs/io-θv,

(21)

iCVT=ωs/io-ωv,

(22)

dθt/dt=ωs/io-ωv,

(23)

dωe/dt=iCVT·dωs/dt+ωs·diCVT/dt.

(24)

式中：ωe为发动机角速度,ωs为从动轴转速,ωv为车轮角速度,Tin为主动轮输入转矩.

4) 整车模型为

(25)

式中：r为轮胎半径；Ff为地面滚动阻力；Fw为车辆空气阻力；Fi为车辆行驶地面阻力,此处设为零；Fj为汽车加速阻力.

3.2 CVT传感器故障注入模型

CVT传感器的常见故障通常表现为5类,即偏差、增益、短路、断路及噪声干扰.在LSSVM基础上对以上故障进行建模分析.目的在于实现整车故障模式下,容错理论的有效控制.

1)传感器偏差故障为

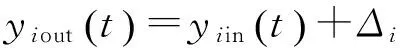
(26)

式中：Δi为偏差常数.

2)传感器增益故障为

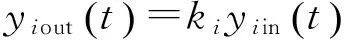
(27)

式中：ki为增益系数.

3)传感器短路故障为

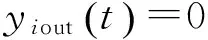
(28)

第i个传感器输出为常值0.

4)传感器断路故障：

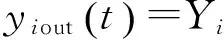
(29)

式中：Yi为传感器输出信号的极值,为常数.

5)传感器噪声干扰故障为

(30)

式中：rni(t)为持续白噪声干扰.其中,故障注入代码“0”无故障,“1”偏差,“2”增益,“3”短路,“4”断路,“5”噪声干扰.

3.3 无级变速器控制系统动态仿真模型

针对车辆实际行驶工况下无级变速器液压系统油门开度α、转速n、转矩T、从动油缸压力p、速度V、目标夹紧力、目标速比、油压输入、功率输入信号等变化及功率匹配,利用容错控制理论在MATLAB/Simulink中建立无级变速器系统硬件在环仿真动态模型,如图10所示.

为了验证容错控制在CVT产生故障时的效果,对比了速比控制及从动油缸压力控制在出现故障后,有无容错控制对比如图11～16所示.

从图11、12可以看出,无故障下,目标速比在限制范围内可以达到最大速比2.5.从图13、14可以看出,当出现故障后,实际速比迅速升高.从图15、16可以看出,经过容错控制后的实际速比无限接近最大速比,这样可以稳定系统运行.从动油缸压力在无故障的情况下维持在4.25 MPa波动,在出现故障后实际压力迅速上升.经过容错后的从动油缸压力最终维持在目标压力附近,保证了系统的稳定性,两者的容错率均可达到98.728%.由此证明,本文运用IABC-LSSVM对故障参数提取在CVT故障诊断中的合理性.

图10 CVT系统硬件在环仿真动态模型Fig.10 System hardware-in-loop dynamic simulation model of CVT

图11 无故障下目标速比与实际速比Fig.11 Target ratio compare with real ratio under no-failure

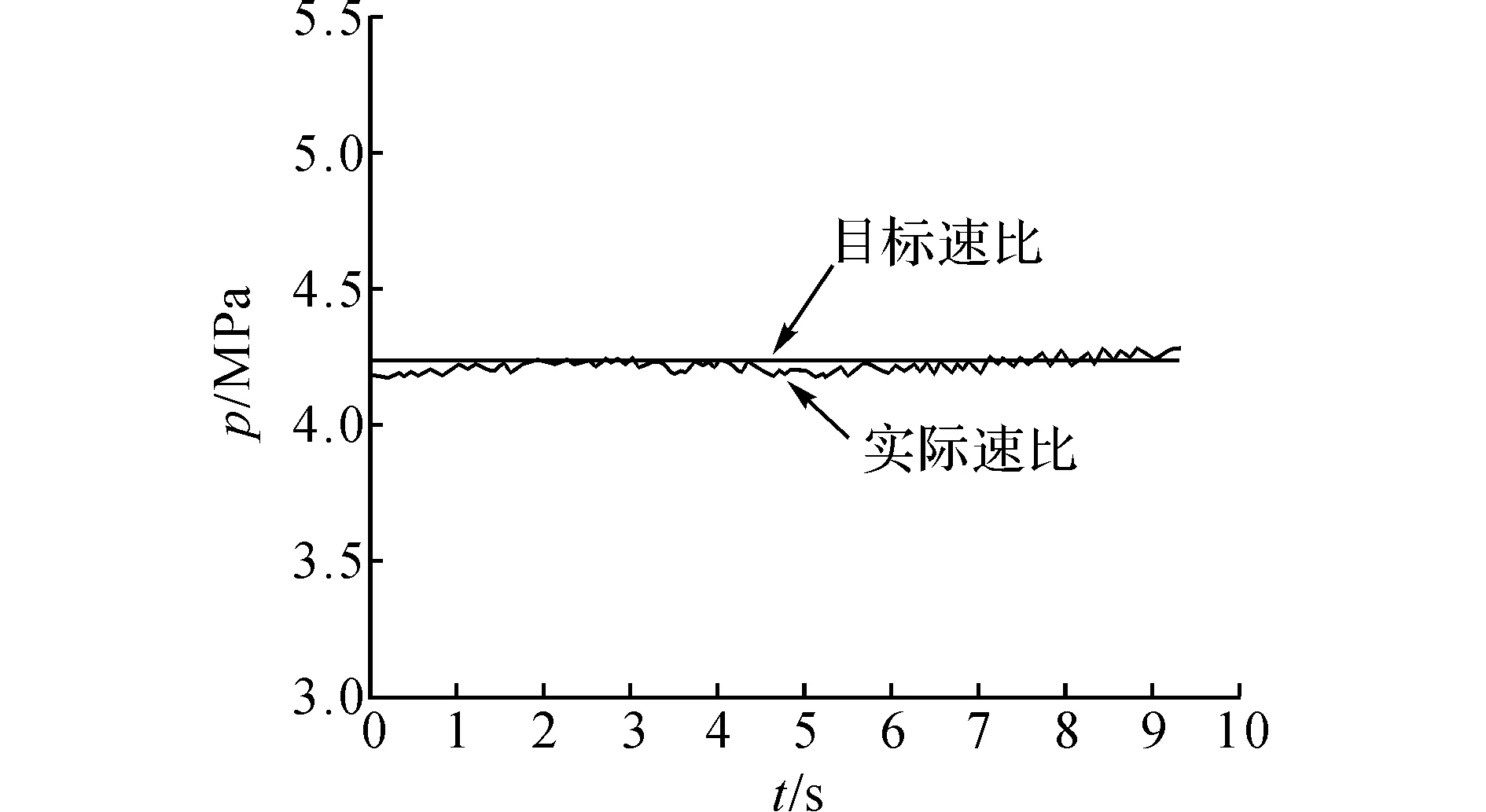
图12 无故障下目标压力与实际压力Fig.12 Target pressure compare with real pressure under no-failure

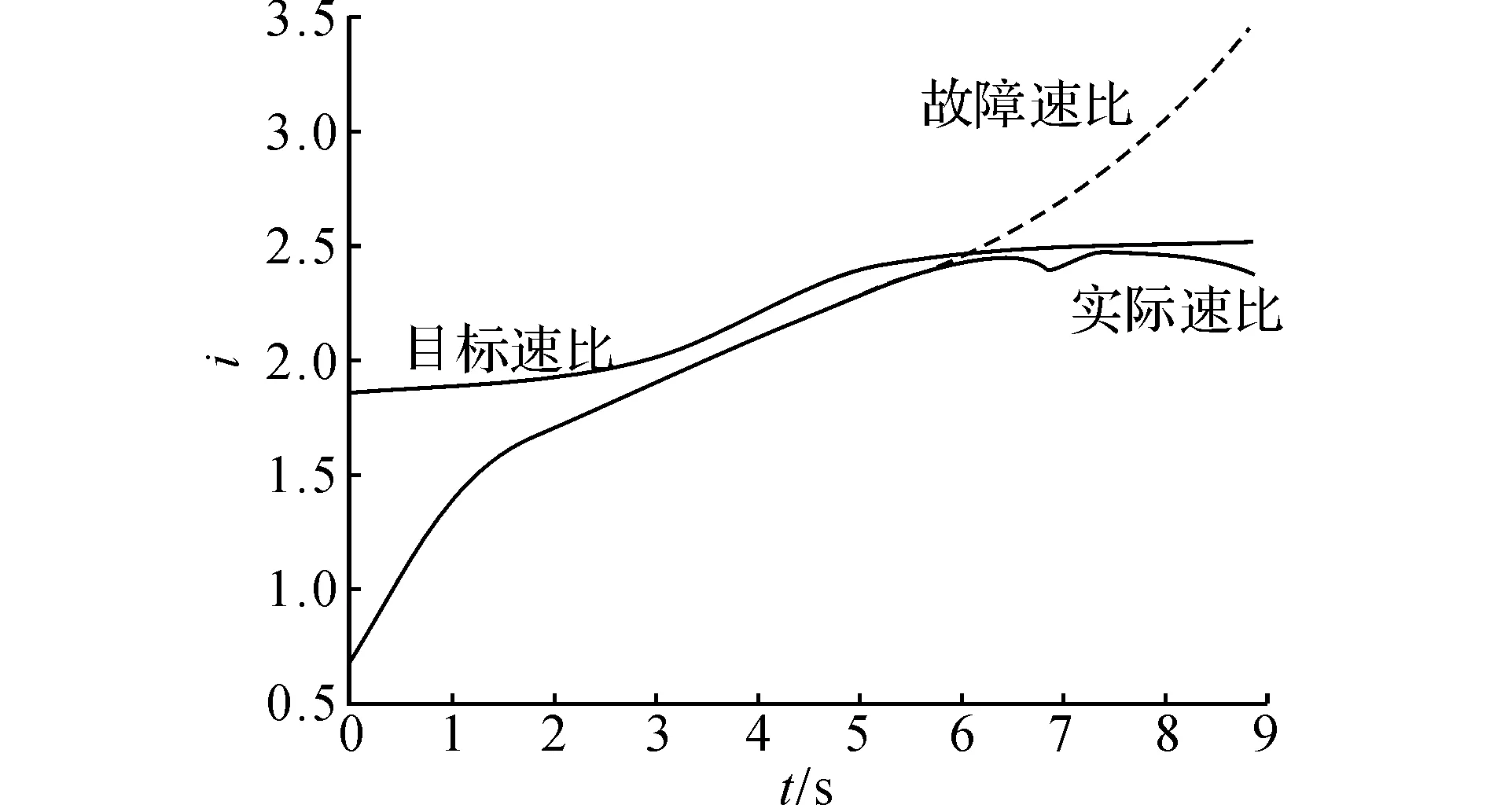
图13 故障目标速比与实际速比Fig.13 Target ratio compare with real ratio under failure

图14 故障目标压力与实际压力Fig.14 Target pressure compare with real pressure under failure

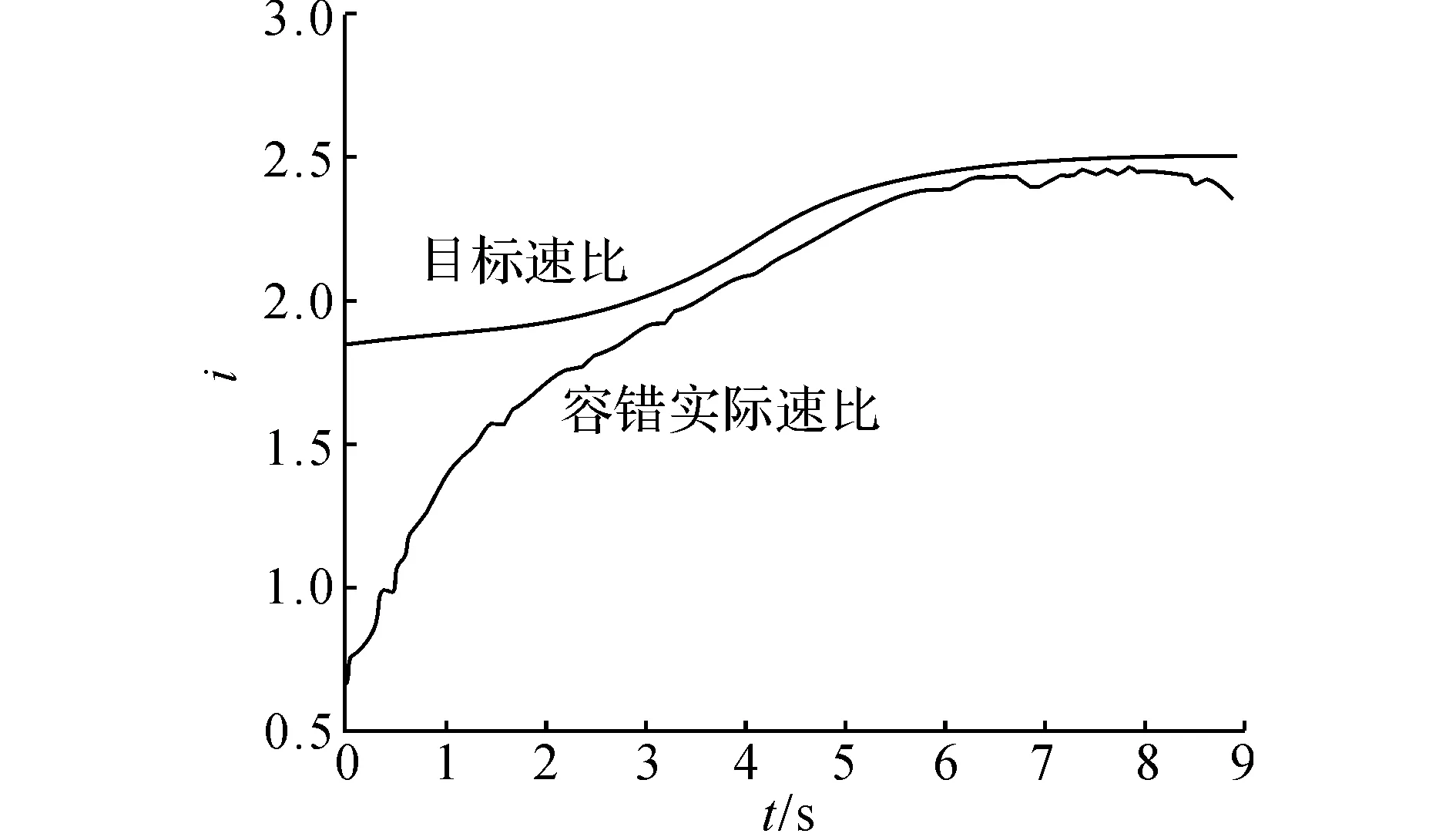
图15 经容错控制后的目标速比与实际速比Fig.15 Target ratio compare with real ratio after fault-tolerant

图16 经容错控制后的目标压力与实际压力Fig.16 Target pressure compare with real pressure after fault-tolerant

4 结 论

(1)提出用于CVT故障诊断的多特征组分析方法.该方法在不增加过多硬件设备和过大运算量的前提下,利用容错解析冗余的控制方法对CVT电液控制系统故障进行诊断,在此基础上建立了无级变速器硬件在环仿真动态模型.

(2)采用IABC-LSSVM法获取CVT全局与局部零部件特征参数,建立夹紧力控制系统与速比控制系统的故障预测模型.按照故障模型进行分类辨识,针对提取的部分故障特征向量进行仿真分析.

(3)在MATLAB/Simulink中建立硬件在环动态仿真,分析CVT无故障和产生故障情况下,经容错理论控制,系统在“跛行”状态下的对比效果.结果表明：利用该方法实现了对CVT在线故障诊断及容错控制,且容错识别精度较高可达99.728%,较其他参数提取的算法效率和解的质量更高.综合以上分析,结合提出的方法,对提高CVT电液控制系统的可靠性及稳定性具有重要意义.

[1] 韩玲.无级变速器电液控制系统关键技术研究[D].吉林：吉林大学,2015.

HAN Ling. Research on the key technology of the electric-hydraulic system of continuously variable transmission [D]. Jilin: Jilin University, 2015.

[2] 田承伟,宗长富,王翔,等.线控转向汽车传感器的容错控制[J].吉林大学学报：工学版,2010,40(1): 6-12.

TIAN Cheng-wei, ZONG Chang-fu, WANG Xiang, et al. Sensor fault tolerance control method for steer-by-wire car [J]. Journal of Jilin University: Engineering and Technology, 2010, 40(1): 6-12.

[3] 杨柳青,陈无畏,张荣芸,等.基于控制律重组的汽车主动悬架容错控制与试验[J].农业机械学报,2013,44(10): 1-9.

YANG Liu-qing, CHEN Wu-wei, ZHANG Rong-yun, et al. Fault-tolerant control and experiment on vehicle semi-active suspension system based on control law reconfiguration [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(10): 1-9.

[4] 宗长富,李刚,郑宏宇,等.线控汽车底盘控制技术研究进展及展望[J].中国公路学报,2013,26(02): 160-176.

ZONG Chang-fu, LI Gang, ZHENG Hong-yu, et al. Study progress and outlook of chassis control technology for X-by-wire automobile [J]. China Journal of Highway and Transport, 2013, 26(02): 160-176.

[5] ATAUR R, SAZZAD B, AKM M, et al. Energy efficient electromagnetic actuated CVT system [J]. Journal of Mechanical Science and Technology, 2014, 28(4): 1153-1160.

[6] AKEHURST S, VAUGHAN N D, PARKER D A, et al. Modeling of loss mechanisms in a pushing metal V-belt continuously variable transmission. Part2: pulley deflection losses and total torque loss validation [J]. Proceedings of Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2004, 218(11): 1283-1293.

[7] 王国芳,方舟,李平.基于批量递归最小二乘的自然Actor-critic算法[J].浙江大学学报：工学版,2015,49(07): 1335-1342.

WANG Guo-fang, FANG Zhou, LI Ping. Natural actor-critic based on batch recursive least-squares [J]. Journal of Zhejiang University: Engineering Science, 2015, 49(07): 1335-1342.

[8] 陈昌富,龚晓南,王贻荪.自适应蚁群算法及其在边坡工程中的应用[J].浙江大学学报:工学版,2003, 37(10): 70-73.

CHEN Chang-fu, GONG Xiao-nan, WANG Yi-sun.Adaptive colony algorithm and its application to the slope engineering [J]. Journal of Zhejiang University: Engineering Science, 2003, 37(10): 70-73.

[9] 刘路,王太勇.基于人工蜂群算法的支持向量机优化[J].天津大学学报：2011,44(09): 803-809.

LIU Lu, WANG Tai-yong. Support vector machine optimization based on artificial bee colony algorithm [J]. Journal of Tianjin University, 2011, 44(09): 803-809.

[10] 李鑫滨,陈云强,张淑清.基于改进ABC算法优化的LSSVM多分类器组机械故障诊断模型[J].中国机械工程,2013, 24(16): 2157-2163.

LI Xin-bin, CHEN Yun-qiang, ZHANG Shu-qing. Mechanical fault diagnosis model based on IABC algorithm optimized multiple Lssvm classifier group [J]. China Mechanical Engineering, 2013, 24(16):2157-2163.

[11] 岳云力. 基于改进人工蜂群算法的机组组合优化方法[D].杭州：浙江大学,2012.

YUE Yun-li. Method of unit commitment based on an improved artificial bees colony algorithm [D]. Hangzhou: Zhejiang University, 2012.

[12] 张伟.人工蜂群混合优化算法及应用研究[D].杭州: 浙江大学,2013.

ZHANG Wei. Research on artificial bee colony based hybrid optimization algorithms and applications [D]. Hangzhou: Zhejiang University, 2013.

[13] KOBAYASHI D, MABUCHI Y, KATOH Y. A study on the torque capacity of a metal pushing V-belt for CVT [J]. SAE Transactions, 1998, 2(8): 31-39.

[14] RAYMOND F W, KATHERINE M R. CVT lubrication: the effect of lubricants on the frictional characteristics of the belt-pulley interface [J]. Tribo Test, 2006, 6(2): 151-170.

[15] SUN J D, FU W Y, LEI H, et al. Rotational swash plate pulse continuously variable transmission based on helical gear axial meshing transmission [J]. Springer Journal, 2012, 6(04): 1138-1142.

[16] SAZZAD B S, HOWWAIN A. Kinematics and non-linear control of electromagnetic actuated CVT system [J]. Journal of Mechanical, Science and Technology, 2012, 26(07): 2189-2196.

Faults diagnosis and classification based on fault-tolerant theory for continuously variable transmission

HAN Ling1, LU Yan-hui2, AN Ying3, TIAN Li-yuan1

(1.SchoolofMechatronicEngineering,ChangchunUniversityofTechnology,Changchun130021,China;2.CollegeofAutomotiveEngineering,JilinUniversity,Changchun130022,China;3.CollegeofAutomotiveEngineering,HunanUniversity,Changsha410000,China)

The fault vectors were extracted by feature extraction of continuously variable transmission (CVT) based on the improved artificial colony algorithm combining with least squares support vector machine in order to fulfill the requirements about on-line fault diagnosis and classification of CVT. The fault predicting models of clamping force and ratio were established. The faults location and identification classification were based on predicting models. Parts of fault feature vectors for second cylinder pressure, ratio, and actuator were extracted to simulation by Matlab. The classification of feature vectors after the fault-tolerant controlled was analyzed by simulation curve change trend. CVT was built hardware-in-the-loop simulation by fault-tolerant with Matlab/Simulink. Results showed that the probability of continue working reached 98.728% by using the method for fault-CVT, and the needs of CVT reliability and stability for the online fault diagnosis were meeted.

continuously variable transmission; fault-tolerant; improved artificial bees colony algorithm; fault diagnosis

2015-08-27.

国家自然科学基金资助项目(50775094).

韩玲(1984—)，女，博士，讲师，从事车辆工程研究. ORCID: 0000-0002-8574-7028.E-mail: hanling@ccut.edu.cn.com

卢延辉，男，副教授. ORCID: 0000-0002-1360-9830.E-mail: luyh@jlu.edu.cn

10.3785/j.issn.1008-973X.2016.10.012

U 472

A

1008-973X(2016)10-1927-10

浙江大学学报(工学版)网址： www.zjujournals.com/eng