电磁轴承-柔性转子系统多目标加权的主动振动控制

蒋科坚, 祝长生

(1. 浙江理工大学 信息学院,浙江 杭州 310018; 2. 浙江大学 电气工程学院,浙江 杭州 310027)



电磁轴承-柔性转子系统多目标加权的主动振动控制

蒋科坚1,2, 祝长生2

(1. 浙江理工大学 信息学院,浙江 杭州 310018; 2. 浙江大学 电气工程学院,浙江 杭州 310027)

为了避免影响系数法求解出一个过大的校正力计算结果,解决由此造成的电磁力饱和以及转子悬浮失稳问题,拓展基于最小二乘法的影响系数法,提出多目标价值函数混合加权的柔性转子振动主动控制方法.利用多个目标价值函数的加权设计,不仅实现了多个节点振动之间按权值实现振动抑制,而且能够在不同量纲的振动幅值和所需电磁力之间实现权衡.算例仿真表明,提出的控制方法可以在实现转子振动控制的同时,顾及到电磁轴承(AMB)电磁力的能力极限.在转子振动能够控制在允许的范围内,适当减小对电磁力的需求,降低对电磁轴承的功率要求.

柔性转子；电磁轴承(AMB)；影响系数法；主动振动控制

主动电磁轴承(active magnetic bearing, AMB,以下简称电磁轴承) 是一种新型的转子磁悬浮支承技术.电磁轴承作为转子振动主动控制器件,可以通过施加电磁力对转子振动进行主动控制.电磁轴承的悬浮支承为转子系统动力学和转子振动抑制提出了新的研究内容.

从原理上区分,柔性转子的振动控制方法可以分为两大类：模态法(modal method)和影响系数法(influence coefficient method).模态法的基本思想是根据转子不平衡量可以按振动模态分解成多个正交不平衡分量,每一分量只能激励起相应的一个振动模态的动力学理论.影响系数法直接以激励力和转子节点振动之间的关系实现控制.与模态法不同,影响系数法的最大优点是与转子的振动模态信息无关,不依赖于控制对象的数学模型.实践证明,在转子振动的线性范围内,采用影响系数法可以获得较好的控制效果.

柔性转子动力学及其振动控制研究已有较长的历史,但有关采用电磁轴承抑制柔性转子振动的研究相对较少.Stephen[1]指出对柔性转子的振动控制,无法通过转子上有限数量的位置(离散的,有限个节点)施加电磁力,消除整个连续转子的振动,并提出多目标节点的柔性转子振动抑制方法.Arias等[2]为双盘柔性转子建立有限元模型,每个轴端视为欧拉梁模型,开展不平衡振动的建模和控制.Tseng等[3]提出根据影响系数法计算不平衡量,以卡尔曼滤波器实现测量噪声消除的转子实时动平衡方案.Kang等[4]采用基于影响系数法的自动平衡方法,其中不平衡质量修正用神经PD控制.谢振宇等[5]通过实验发现,调节电磁轴承的支承刚度和阻尼能够明显改变柔性转子的平动和锥动两个刚体临界转速,但对一阶弯曲固有频率的影响很小.Xu等[6]开展基于电磁轴承的柔性转子过弯曲临界的实验,其团队在“十五”和“十一五”863重点项目支持下,完成了10 MW高温气冷堆发电机磁轴承实验台架的设计工作.李红伟等[7]采用影响系数法和振型平衡法,分别对转子的刚性模态和前两阶挠性模态进行该机动平衡.

目前,在基于电磁轴承的柔性转子振动控制中,影响系数法是普遍采用的方法.影响系数法往往会得出过大的、超出电磁轴承实际能力的计算结果.由于电磁轴承的悬浮控制和振动控制是叠加在一起的,电磁力一旦饱和,不只是转子振动控制效果变差,更严重的是破坏了转子悬浮控制的反馈机制,造成转子失稳,甚至跌落事故.其次,在转子振动控制中,目标节点振动最小化不是评判最优的唯一标准.控制设计必须考虑电磁轴承的功率极限和成本.在振动可接受的范围内,解决好所需电磁力要求和振动控制效果的灵活权衡.

已有研究在影响系数法中引入最小二乘法,目的是解决经典影响系数法中目标节点数量不能大于激励节点数量的控制问题.本文拓展了最小二乘法的思路,在价值函数中不仅包含节点振动,还加入了电磁力的因素,使得控制方法不仅可以抑制转子各节点的振动,还可以在电磁力和转子振动之间实现灵活调控.以较小的电磁力,将转子振动抑制在允许范围内.

本文的仿真算例以KEOGH[8-12]实验室的电磁轴承-柔性转子实验平台为对象.转子有限元建模软件和模态分析软件来源于该实验室.以有限元转子模型为核心,本文构建提出转子振动抑制方法的控制模型,验证了控制效果.

1 影响系数法及最小二乘法简介

转子上需要进行振动抑制的节点称为目标节点；施加矫正力的节点称为激励节点.在线性范围内,目标节点的运动与外激励力之间可以表示为如下关系：

(1)

式中：n为目标节点的数量,A为目标节点的当前振动,B为目标节点的原始振动,m为激励节点的数量,W为各个激励节点上施加的矫正力；C为影响系数矩阵,是维复数矩阵,描述了在m个激励节点施加单位激励后,在n个目标节点上引起响应的矩阵关系.

假设在激励W作用下,目标节点的振动响应为A1；激励改变为W2,目标节点响应变为A2,则有

A1=CW1+B ,

A2=CW2+B .

(2)

为了使激励W2能够完全抑制目标节点的振动,即A2=0,可得

W2=W1-C-1A1.

(3)

可见,在系统线性且C已知的前提下,可以通过式(3)准确地求得激励力W2,使得激励后的转子振动为零.以上所述是影响系数法的基本思想.

式(3)中存在C-1项,因此必须n=m,C为方阵时式(3)才能求解；否则,C-1不存在.当n≠m时,式(3)的求解方法无效.

结合最小二乘法的影响系数法被提出,可以使得目标节点的数量不受限制.

最小二乘法的控制目标是追求在某个转速下所有目标节点振动的平方和为最小.首先,根据每个目标节点的振动要求,定义每个目标节点振动的评价权值,是n×n对角矩阵Q,

(4)

式中：元素qi为第i目标节点振动的权值.

最小二乘法以各节点振动幅值的平方和加权最小化为价值函数,即

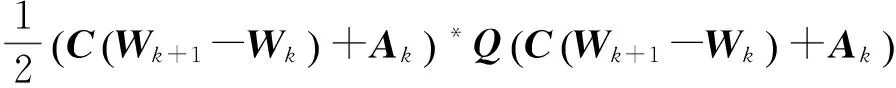
(5)

式中：A为目标节点的振动；*表示矩阵的Hermitian变换,即转置加共轭.式中的1/2是为了推导公式的格式整齐,无特别意义.下标k和k+1为离散控制中每个离散时刻的顺序编号.

式(5)中,C、Wk及Ak都为已知量.为了在k+1时刻的激励力Wk+1能够使目标函数J为最小极值,可以通过对J求Wk+1的偏导为零得到,即

(6)

通过式(6)可以解得,使价值函数J为最小极值,用Wopt表示：

(7)

式(7)为采用最小二乘法的影响系数法公式.可知,倘若C为方阵,且Q为单位矩阵,式(7)与(3)是完全等价的.

最小二乘法解决了经典影响系数法中目标节点的数量限制问题,但采用最小二乘法控制是有残余振动的.最小二乘法追求目标节点振动的加权平方和为最小,即价值函数最小.

2 多价值函数混合加权的控制方法

对于电磁轴承的工业应用,有限的电磁力是主要的技术瓶颈之一.要产生更大电磁力,必然需要更大体积的电磁轴承和更高驱动能力的控制系统.对于转子振动的最优控制,目标节点振动最小化不是唯一的最优评判标准,所需电磁力最小化是一个重要的考虑因数.为此,提出多价值函数混合加权的控制方法,在价值函数中加入电磁力的因素.

与节点振动权值矩阵Q类似,电磁力权值矩阵R为m′m对角矩阵,

(8)

式中：m为激励节点数量,ri为根据各个电磁轴承的驱动能力确定的电磁力之间的权值.当各个电磁轴承相同时,R可以取为单位矩阵.

建立一个转子振动最小化和电磁力最小化的综合最优控制价值函数：

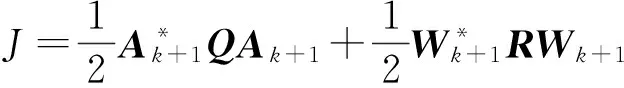
(9)

如果直接使用式(9)为价值函数,由于转子振动和电磁力的物理量纲不一致,即A*A和W*W两个量的数值可能不在一个数量级上,那么数值较大的量在综合价值函数中占绝对主导地位,而数值较小量则无关紧要.必须增加一个混合权值参数：

(10)

式中：p和q分别为节点振动和电磁力的混合权值参数,作用是将两个不同物理量调整至相同的数量级,使之在数值上具有可比性.

价值函数J与转子振动Ak、激励力Wk及Wk+1的关系为

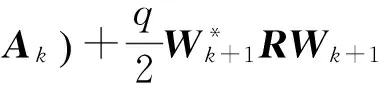
(11)

对目标函数J求Wk+1的偏导为零时,目标函数J为最小值,即

(12)

根据式(12),可以解得目标函数J为最小极值的Wopt：

Wopt=Wk+1=

(13)

式(13)是提出的能综合权衡转子振动和所需电磁力的控制计算公式.

3 主动控制仿真

3.1 仿真算例

图1 柔性转子算例的结构和尺寸Fig.1 Example of flexible rotor system

仿真算例的基本结构如图1所示.它由一根均质等直径轴和4个刚性圆盘组成.轴的长度为1 930 mm,轴的直径为50 mm.每个圆盘的质量约为10 kg.转子采用有限元法建模,电磁轴承的转子轴颈部分视为刚性圆盘.具体的建模方法请参阅有关转子动力学教科书,本文限于篇幅,不详细叙述.根据转子的结构分为6个节点,如图1所示.仿真假设,转子的不平衡质量只集中在4个刚性圆盘上,忽略其余部分的不平衡质量.4个刚性圆盘的不平衡质量都设置为1 g·mm,角度分别为4个盘从左到右[0,p/2,p,-p/2].仿真中,影响系数采用事先离线测定,控制中实时查表获取.

电磁轴承悬浮控制采用4个径向自由度离散的PID控制.仿真中,电磁轴承工作在4.3 A的偏置电流下,位移刚度系数为2×106N/M,电流刚度系数为487 N/A.

在电磁轴承等效刚度为106N/M,等效阻尼为4 800 N·s/m的条件下,采用模态软件分析算例转子的前四阶模态振型和对应的临界转速,如图2所示.其中,锥形涡动和平行涡动为刚体振型,一阶弯曲和二阶弯曲为柔性弯曲振型.以下所有仿真都是在该支承条件下进行的.

图2 算例转子的前四阶模态振型Fig.2 First four vibration modes of example

3.2 最小二乘法的控制仿真

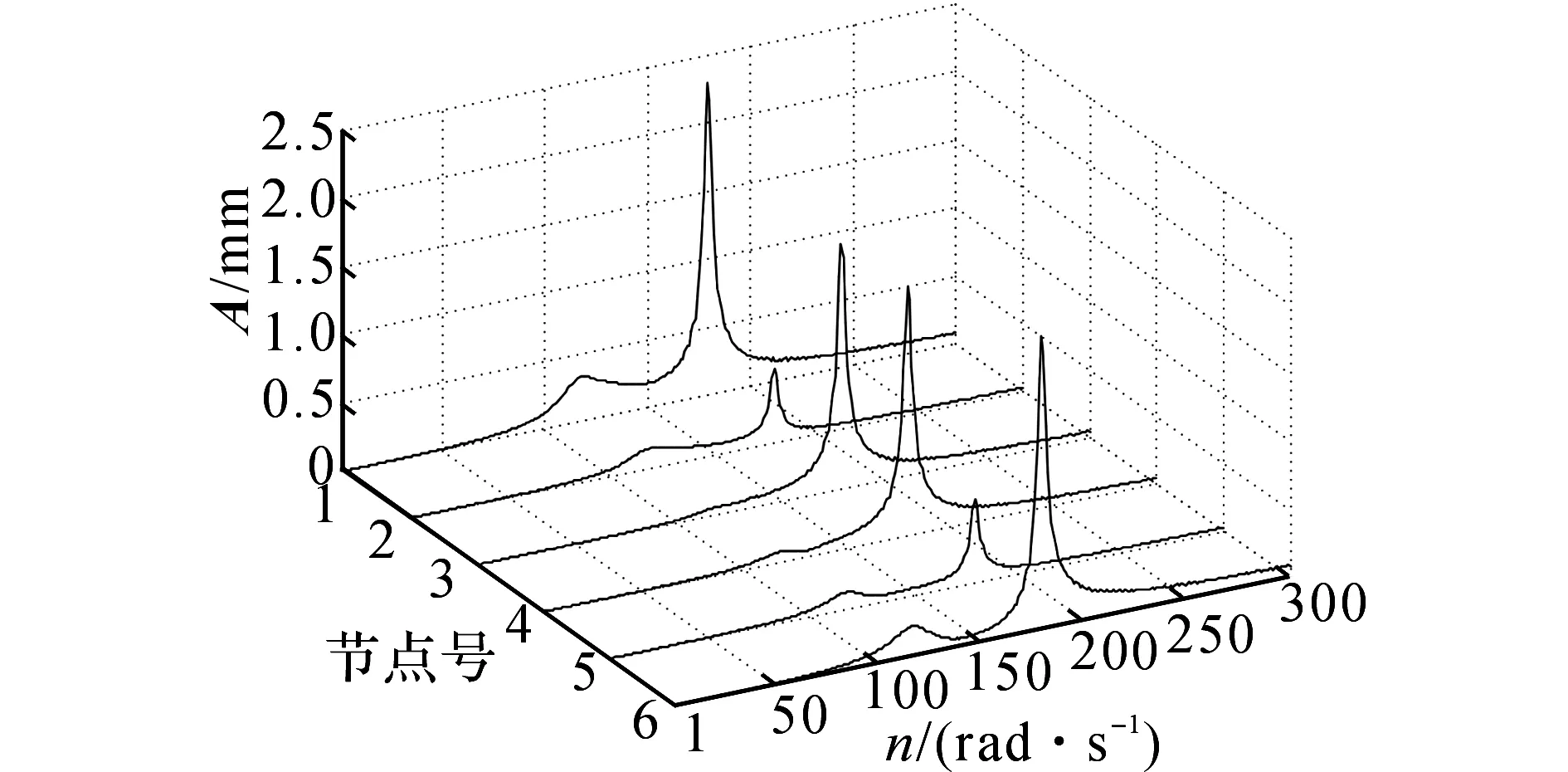
图3 1～300 rad/s转子各节点的原始振动Fig.3 Original vibration of rotor in 1-300 rad/s

检测并记录转子所有6个节点在1～300 rad/s转速下的原始振动,如图3所示.图中，n为转速.由图3可见,由于平动和锥动两个刚体临界距离较近,两个峰值区别不明显,模糊为一个峰值.一阶弯曲临界非常清楚,在178.6 rad/s处峰值较高.

采用经典的影响系数法,以2个电磁轴承作为激励节点,实现2个目标节点的振动抑制.电磁轴承在2号和5号节点.

开展2个仿真过程.如图4所示为当节点2和5既作为激励节点,又作为目标节点时,转子全部6个节点的振动变化情况.如图5所示为以节点3、4为目标节点时,转子各节点的振动变化情况.

从图4、5可见,采用影响系数法的振动控制对指定目标节点的振动抑制效果十分有效,能够很好地抑制目标节点的振动.需要特别指出的是,图4、5都显示在一阶弯曲临界转速位置有一点点小凸起,

图4 以2、5为目标节点的经典影响系数法控制Fig.4 Vibration control for node 2 and node 5 with classic influence coefficient method

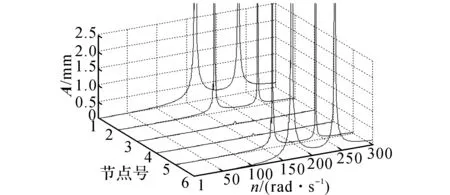
图5 以3、4为目标节点的经典影响系数法控制Fig.5 Vibration control for node3 and node4 with classic influence coefficient method

表明还有一些残余振动.经反复验证和数据核对发现,由于仿真采用阶梯形阶跃升速,阶跃幅度为1 rad/s,每次阶跃稳定时间为3 s,然后记录振动数据.由于在一阶临界转速附近,转子振动变化剧烈,稳定时间相对不够长,造成了残余振动.依据影响系数法理论可知,只要稳定时间足够长,可以完全抑制目标节点的振动,没有残余振动.

从图4、5可以看出,由于影响系数法是以消除目标节点的振动为控制目标,没有顾及其他节点的振动；其他非目标节点上的振动可能大幅增强.更糟的情况是影响系数法的控制结果在未知的转速下引起了新的振动峰值,如图4所示大约在300 rad/s,图5所示在250 rad/s左右都有一个新的振动峰值.分析后发现,由于电磁轴承在这一转速对目标节点的控制能力较弱,即影响系数较小,必须产生很大的电磁力才能抑制目标节点的振动.此时,这个巨大的电磁力已在其他非目标节点上产生不期望的强烈振动.

采用结合最小二乘法的影响系数法进行仿真,检验该方法能够兼顾多个目标节点,甚至转子的整体振动抑制的能力.

以电磁轴承节点2、5为激励节点,以全部节点1～6为目标节点,取各目标节点的振动权值都相等,即Q为单位矩阵.如图6所示为在1～300 rad/s速度下的振动控制效果.

从图6可见,控制效果与图4、5有很大差异.在最小二乘法策略下,对减小转子整体振动的效果十分有效.最重要的是因为最小二乘法能够兼顾每个节点的振动,不会发生在非目标节点引起额外振动的情况.

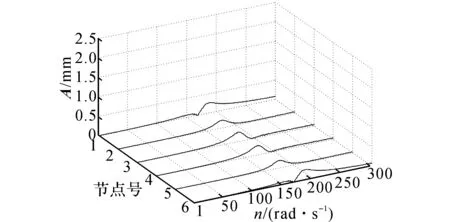
图6 结合最小二乘法的影响系数法仿真Fig.6 Vibration control for all nodes with least squaremethod

图7 节点2的两种控制效果比较Fig.7 Vibration contrast of node 2 between two controlmethods

将图4中节点2的振动曲线与图6中节点2的振动曲线进行比较,按同样比例显示在图7中.可见,经典影响系数法对目标节点振动的抑制效果十分理想,只有因为稳定时间不够引起的微量残余振动.追求目标节点的振动完美抑制,可能需要很大的电磁力,而过大的电磁力会加剧其他节点的振动.可能只要对目标节点振动做很小的牺牲,就可以换来对整个转子其他节点振动的整体大幅下降.最小二乘法能够很好地实现这一点.

3.3 多价值函数混合加权的控制仿真

在图6的最小二乘法的仿真中,两个电磁轴承在y方向(垂直方向)所产生的电磁力变化幅值被记录,如图8所示.在超越一阶弯曲临界转速的时刻,左、右两个电磁轴承所需产生的电磁矫正力波动幅值达到的最大值约为190和150 N.

图8 最小二乘法振动控制的电磁力变化Fig.8 Magnetic force in least square method

在进行此项仿真前,先讨论式(10)中混合权值p和q的物理含义和取值依据.p为节点振动幅值平方的权值,根据已有仿真数据,转子振动大致在0.1 mm数量级,即p为10-8m2数量级.q为电磁力平方的权值,电磁力大致在10 N数量级,即q为102N2数量级.当p∶q=1010时,表示转子0.1 mm的振动和10 N的电磁力是等权的.通俗地讲,在控制中允许以转子振动增大0.1 mm为代价,使得电磁力减小10 N；相反,可以增大10 N电磁力为代价,换来转子振动减小0.1 mm的改善.

采用p∶q=1010的混合加权控制进行仿真,Q、R都取相应维数的单位矩阵.电磁力变化的仿真结果如图9所示.转子6个节点的振动的变化如图10所示.将图9、10分别与图8、6比较,采用电磁力与转子振动混合权值最优控制后,左、右两个电磁轴承所需产生的最大矫正力波动幅值分别减小到125和120 N,而各节点的振动都普遍小幅增大.

增加电磁力权重,取p∶q=0.2×1010进行仿真,电磁力变化和各节点振动情况记录如图11、12所示.可见,由于电磁力的权重的增大,左、右两个电磁轴承所需产生的最大矫正力波动幅值分别减小到约60和60 N,但各节点的振动进一步增大.

仿真算例表明,采用电磁力与转子振动混合权值最优控制方法,可以根据产生电磁力的能力和转子振动的实际允许范围,灵活调配电磁力需求与转子振动的权衡比例.

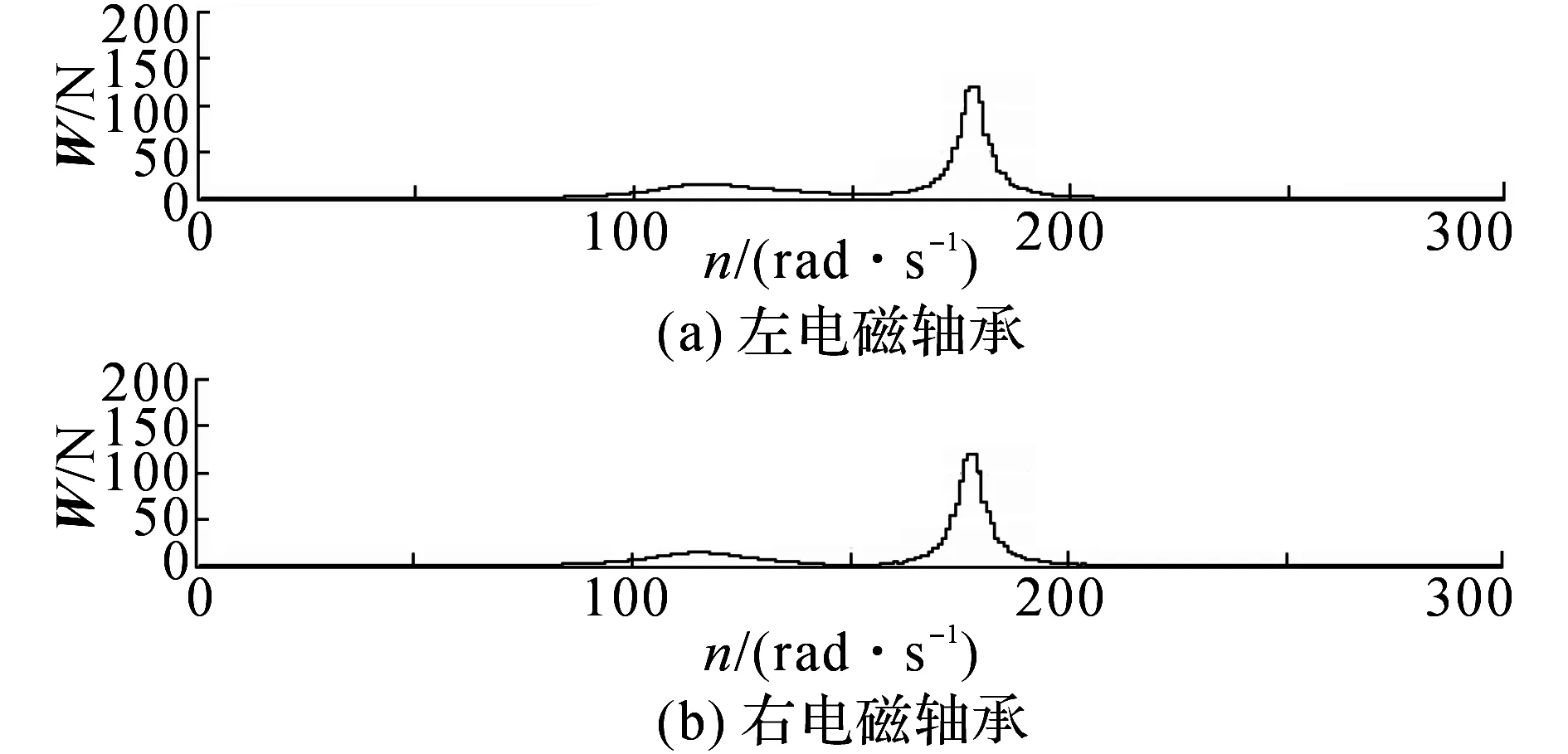
图9 p∶q=1010时的电磁力变化Fig.9 Magnetic force with p∶q=1010

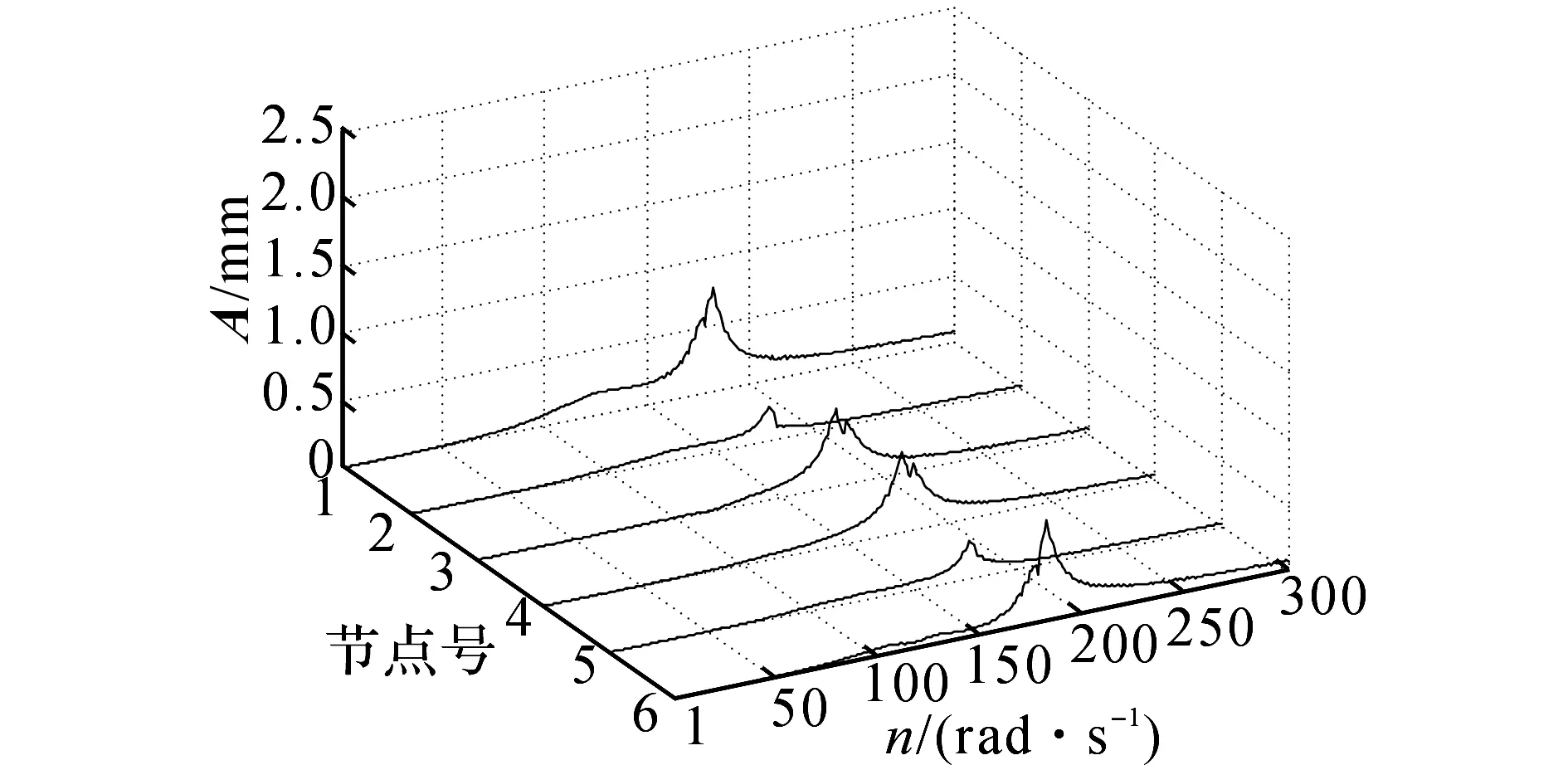
图10 p∶q=1010时的各节点振动情况Fig.10 Vibration control with p∶q=1010

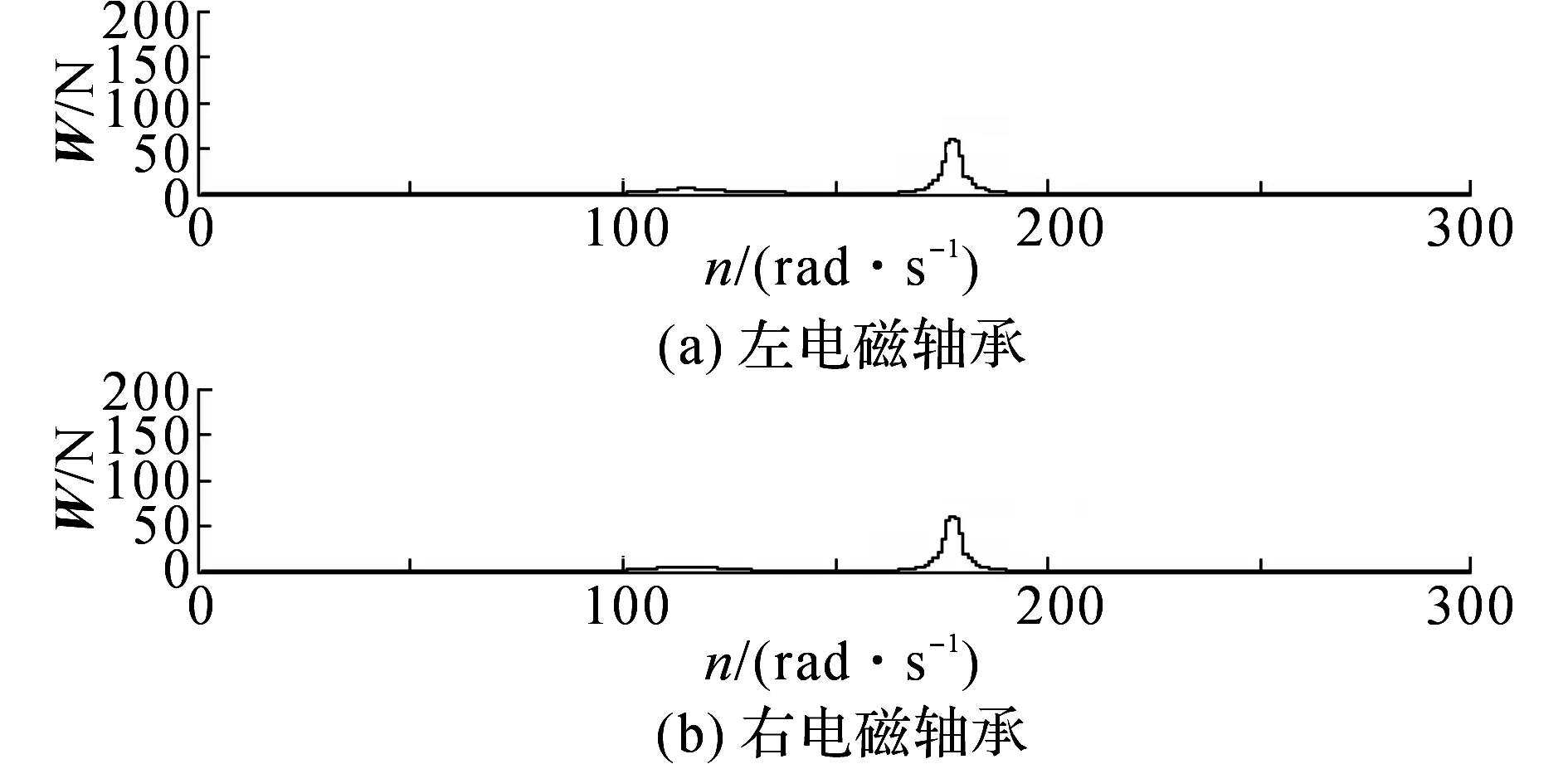
图11 p∶q=0.2×1010时的电磁力变化Fig.11 Magnetic force with p∶q=0.2×1010

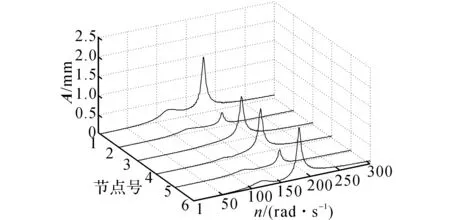
图12 p∶q=0.2×1010时的节点振动情况Fig.12 Vibration control with p∶q=0.2×1010

4 结 论

(1) 结合最小二乘法的影响系数法,解决了目标节点数量不能大于激励节点数量的矛盾,使得目标节点数量不受限制.它的实质是对某些节点的振动作少量牺牲,换来对整个转子其他节点振动的整体大幅下降.

(2) 提出多价值函数混合加权的控制方法,不仅可以在多个节点振动之间按权值比例实现振动调配,而且可以对节点振动和所需电磁力之间实现权值调控.目的是可以在转子振动允许范围内,适当降低对电磁力的要求,用较小的电磁力,得到可以接受的转子振动抑制效果.

(3) 提出的转子振动抑制方法是建立在影响系数法基础上的,所以应用效果和应用局限与影响系数法一样,必须满足转子振动的激励和响应在线性范围或近似线性范围内.

[1] STEPHEN W. Adaptive optimal control of active balancing systems for high-speed rotating machinery [D]. Michigan: The University of Michigan, 1999.

[2] ARIAS M, SILVA G. Finite element modeling and unbalance compensation for a two disks asymmetrical rotor system [C]∥ 5th International Conference on Electrical Engineering, Computing Science and Automatic Control. Mexico City: [s.n.], 2008: 386-391.

[3] TSENG C, SHIH T, LIN J. A Kalman filter-based automatic rotor dynamic balancing scheme for electric motor mass production [C]∥ The Proceedings of Materials Science Forum(Vols: 505-507). Switzerland: [s.n.], 2006: 997-1002.[4] KANG Y, LIN T, CHU M. Design and simulation of a neural-pd controller for automatic balancing of rotor[C]∥ 3rd International Symposium on Neural Networks. Chengdu: [s.n.], 2006: 1104-1109.

[5] 谢振宇,徐龙祥,李迎,等.控制参数对磁悬浮轴承转子系统动态特性的影响[J].航空动力学报,2004, 19(2): 174-178.

XIE Zhen-yu, XU Long-xiang, LI Ying, et al. Influence of control parameters on dynamic characteristics ofactive magnetic bearing system [J]. Journal of Aerospace Power, 2004, 19(2): 174-178.

[6] XU Y, YU H, ZHAO L. Development of a magnetic bearing rotor dynamics analysis software package [C]∥ Proceedings of the 12th International Symposium on Magnetic Bearings. Arlington: [s. n.], 2010: 53-70.

[7] 李红伟,徐旸,谷会东.电磁轴承-挠性转子系统的本机动平衡方法[J].中国机械工程,2008, 19(12): 1419-1428.

LI Hong-wei, XU Yang, GU Hui-dong. Field dynamic balancing method in AMB—flexible rotor system [J]. China Mechanical Engineering, 2008, 19(12): 1419-1428.

[8] CADE I, KEOGH P, SAHINKAYA M. Fault identification in rotor / magnetic bearing systems using discrete time wavelet coefficients [J]. IEEE/ASME Transactions on Mechatronics, 2005, 10(6): 648-657.

[9] SCHLOTTER M, KEOGH P. Synchronous positionrecovery control for flexible rotors in contact with auxiliary bearings [J]. Journal of Vibration and Acoustics, 2007, 129(5): 550-558.

[10] SAHINKAYA M, ABULRUB A, KEOGH P, et al. Multiple sliding and rolling contact dynamics for a flexible rotor/magnetic bearing system [J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(2): 179-189.

[11] KEOGH P. Transient rotor/active magnetic bearing control using sampled wavelet coefficients [J]. Journal of Engineering for Gas Turbines and Power, 2006,192(2): 549-555.

[12] COLE M, KEOGH P, SAHINKAYA M, et al.Towards fault-tolerant active control of rotor-magnetic bearing systems [J]. Control Engineering Practice, 2004, 12(4): 491-501.

Vibration suppressing with mixed weight for multi-targets in active magnetic bearing-flexible rotor system

JIANG Ke-jian1,2, ZHU Chang-sheng2

(1.CollegeofInformaticsandElectronics,ZhejiangSci-TechUniversity,Hangzhou310018,China;2.CollegeofElectricalEngineering,ZhejiangUniversity,Hangzhou310027,China)

An exceedingly great magnetic force can often be required by the influence coefficient, so that the magnetic force saturating would destroy the stability of rotor levitating. A vibration suppressing method with mixed weight for multi-cost functions was proposed. Not only the rotor vibration can be given attention, but also the required magnetic force is considered in the cost function. The simulation results indicate that the proposed method can mediate not only among a group of the target nodes vibration, but between the rotor vibration and the required magnetic force. The advantage of the proposed method means that the requirement for the magnetic force of active magnetic bearing (AMB) can be appropriately decreased as long as the rotor vibration is within the allowable range. The method provides the feasible way for the low-power control of AMB.

flexible-rotor; active magnetic bearing (AMB); influence coefficient method; active vibration control

2015-09-19.

国家自然科学基金资助项目(51477155,11272288,11172261);浙江省自然科学基金资助项目(LZ13E070001)；浙江省公益技术应用研究资助项目(2015C31063);先进航空发动机协调创新中心资助项目.

蒋科坚(1972—),男,教授，从事电磁轴承支承特性、转子振动主动控制的研究. E-mail: jkjofzju@163.com

祝长生,男,教授，博导.

10.3785/j.issn.1008-973X.2016.10.014

TH 133

A

1008-973X(2016)10-1946-06

浙江大学学报(工学版)网址： www.zjujournals.com/eng