运用画图策略提高数学素养

吴丰艺

（晋江市青阳街道中和中心小学，福建晋江362200）

运用画图策略提高数学素养

吴丰艺

（晋江市青阳街道中和中心小学，福建晋江362200）

几何直观主要指数学中利用图形描述和分析问题。几何直观能把复杂的、抽象的数学问题变得简明、形象，对于学生探索解决问题的思路很有帮助。充分借助画图这一策略，让学生在分析数量关系、理解算理、解决问题等过程中能变模糊为清晰，变抽象为具体，变复杂为简单。因此要逐渐培学生养成画图的习惯，从而不断提升解决问题的能力，提高数学素养。

几何直观；画图策略；以图求解；以形助数；以图促思

画图策略是指运用画示意图的方式把抽象问题或复杂问题变得更为直观、具体，易于学生理解，帮助学生更好地理顺思路，从而找到解题方法的一种策略。很多学生理解起来比较困难的，甚至会导致思维的模糊和混乱的问题，借助于图形进行分析，就能豁然开朗，柳暗花明，思维变清晰。数学家斯蒂恩曾说过：如果一个特定的问题可以转化为一个图像，那么就整体地把握了问题［1］。诚然，画图策略在分析数量关系、理解算理、解决问题等的过程中有着很大的优势，能变模糊为清晰，变抽象为具体，变复杂为简单。因此在教学中要合理利用画图策略，提高学生的数学素养。

一、以图求解——变模糊为清晰

图形直观、简洁,且利于思考。学生在解决问题的过程中经常会遇到这样或那样的问题，特别是难以理解题目意思的情况下，通常只要画出图形来帮助理解，问题就能迎刃而解了。因此，图形是帮助人类思考的一种极好工具。

在小学低年段的教学中，由于学生的抽象思维能力还比较欠缺，在遇到一些比较复杂的实际问题时，如能运用画图的方法来帮助学生理清关系，学生就能很容易的理解题意，从而正确的解决问题。如一年级第五单元位置与顺序《左右》一课，有一道这样的题目：“小朋友排队，从右往左数，小明站在第6个，从左往右数，小明站在第5个，这一行共有多少人？”很多学生感到很困难，有的能够感觉出来结果却不会列算式，有的对从右往左数或从左往右数这一个信息感到混乱，因此教学生用画图的方法帮助理解（如图1）：

图1

通过画图，这样学生就很容易列出算式，将模糊的理解变为清晰。

图形不仅直观简洁利于思考，而且其信息量大，概括性强。因此有关行程问题也经常借助线段图来分析数量关系。行程问题有的比较复杂，常关系到两个物体的速度、路程和运动方向，包含的信息较多，且文字叙述较为繁琐，数量关系难以理解。可是，如用线段、箭头来表示行走的路程和方向就能非常直观的表示出路程之间的数量关系。比如：《相遇》一课，借助路线图和线段图这种图示语言就能直观地把一段非常繁杂的文字清晰的表示出来（如图2），非常简洁明了。学生借助线段图读懂隐藏的信息，从而提出问题并顺利地解决问题。在这一过程中，学生充分感受到用画示意图的方法整理信息对于解决问题的价值，突显了线段图在解决问题中的作用。

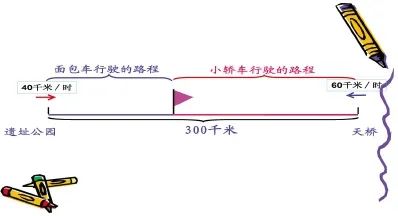
图2

因此，在教学中，要不断的渗透和培养借助画图来帮助理解题意及数量关系的意识和能力，要有意识引导学生学会用画示意图的方法，将题目的意思由模糊变清晰，同时感悟到提炼出的图形既形象又简洁，便于找到解决问题途径的优越性，让学生自主产生画图的愿望，培养几何直观的能力和意识。

二、以形助数——变抽象为具体

“数”与“形”反映的是事物两个方面的属性。我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事非。”［2］数形结合主要指数与形之间的一种一一对应关系。数形结合就是把抽象的数学语言、难以理解的数量关系与直观的几何图形、形象的位置关系联系起来，通过“以形助数”或“以数解形”可以使抽象问题具体化、直观化，以此来帮助理解四则运算的意义及加减法的算理。

三、以图促思——变复杂为简单

2011版课标指出：利用图形描述和分析问题是培养和发展学生的几何直观能力的主要途径。所以，画图表征问题即是解决问题的一种策略，也是一种思维方式［3］。它可以使较为复杂的问题瞬间变得简明、形象、清晰，有助于学生探索解决问题的思路，很快的发现问题的本质，并简化解决的过程。如：公园里原来有一个长24米的长方形绿化带。后来由于重新规划，绿化带的长缩减了6米，这样绿化带的面积就少了60平方米。重新规划后绿化带的面积是多少平方米？很多学生画出示意图后（如图3）：

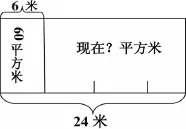
图3

解决问题的方法如下：60÷6=10（米），10×（24-6）=180（平方米）即先求出宽，再根据面积计算公式求出重新规划后的面积。但有一部分学生，根据画出的图形直接列式计算：60×3=180（平方米）。为什么能这么简便的进行计算，虽然很多学生无法一时得以理解，但是在同学与老师的帮助下，通过交流与解释，都能恍然大悟。考察用60×3=180（平方米）这种简便算法的学生的思考过程，应归功于图形给带来的直观的刺激：宽不变，长是6米的3倍，面积也就是减少的60平方米的3倍；更为直接的想法：有个别学生先看减少的部分60平方米，以6米作为标准，根据画出的示意图，重新规划后的绿化带面积就是60平方米的3倍。在这个解决问题的过程中，宽是多少的计算、长方形的面积公式就这样直接跳过，简化了解决问题的步骤。

该例子都充分突显了几何直观的特点：没有经过充分的逻辑推理就能直接洞察事物的本质属性，直达对事物本质的认识及直接把握对象的全貌，从而起到优化解题途径的目的。

总之，运用画图策略，发挥图形的直观性、形象性等特点，将抽象的、复杂的数学语言与直观的、简明形象的图示语言有机地融合在一起，将抽象思维同形象思维有机的结合在一起，充分突显问题的本质，就能很好地帮助学生找到解决问题的思路，开启智慧的大门，发现隐含的条件，突破数学理解上的难点，顺利地使问题得以解决。

［1］钱守旺.教学小学数学并不难［M］,北京：北京大学出版社，2012.

［2］陈蕾.让小学生感受“数形结合”的教学策略［J］.上海教育科研，2016（2）.

［2］林碧珍.数学思维养成课［M］.福州：福建教育出版社，2013.

G623.5

A

1673-9884（2016）09-0045-02

2016-03-13

吴丰艺（1971-），女，福建晋江人，晋江市青阳街道中和中心小学高级教师。