充分挖掘高效利用——高考数学复习课例题讲解技巧分析

于倩倩

（福州市第十八中学，福建福州350000）

充分挖掘高效利用
——高考数学复习课例题讲解技巧分析

于倩倩

（福州市第十八中学，福建福州350000）

结合在高考复习阶段的数学教学案例，围绕如何充分挖掘学生潜力、高效利用例题价值展开思考。教学实践表明，教师可以通过合理的整合、编排、应用，将例题蕴含的思想方法，包含的计算技巧，强化的理论概念充分利用挖掘，鼓励学生进行大胆思考推理，培养他们的数学能力和素养。

复习课；例题；改编；高考

数学是一门抽象科学，单纯的理论过于生涩难懂，例题的讲演，成了数学课的重头戏。尤其是高考复习课的例题，能够帮助同学回顾基础知识，梳理分析思路，总结方式方法。本文结合笔者在高考复习阶段的数学教学案例，阐述了四种不同的例题设置方法，围绕如何充分挖掘学生潜力，高效利用例题价值展开思考与探索。

一、把握节奏，让例题成为“配角”

例题的讲解常用于帮助学生学习方式方法、拓展思路提升思维、巩固和强化概念性质。在《二项式定理》的高考复习课上，笔者采用了2015年新课标I卷的一道选择题作为课前热身题：

例1.（x2+x+y）3的展开式中，x5y2的系数为（）。

A．10B．20C．30D．60

作为引入，旨在通过与高考相关的问题引起学生对于本节知识的重视，并引发学生的思考，唤起学生对于二项式定理的基本知识及使用方法的回忆。故开始教师并不急于让学生立即解答，而是通过提问，让学生回忆二项式定理的基本概念与推导过程。在给予学生充分的思考和整理时间后，教师根据学生的总结，将相关知识进行了梳理、归纳和板书，为本节复习课夯实原理基础。而后，教师再带领学生回归本例，解决问题，而例题这位“配角”的价值也得到了丰富和升华。

通过思考与解决例题的过程，回顾相关的性质定理，掌握解题的思路与技巧，从而达到复习的目的。这样的设置，让学生主动去探索而不是被动接受，比起教师一开始就灌输基本性质定理更加有效。

二、高效课堂，例题选择很重要

无论是书本还是讲义，例题总是层出不穷，变化多端，如果每一题都精讲精练，不仅显得没有层次与重点，也会给师生带来极大的负担和压力，故教师在选择例题时，应精挑细选，尤其是学生进入高考复习阶段，时间紧迫，而且学生知识的储备已日渐丰满，一题多解、综合性强的题型是高效复习的好选择。

相信许多教师在讲评例题或者批改作业的时候，都会遇到以下类似的情形：

下例是一道湖南省高考模拟题：

例2.四边形ABCD中，AB=7，AC=6，cos∠BAC= 11/14，CD=6sin∠DAC，则BD的最大值为。

在前一晚的作业中，教师布置了该题，可做出来的学生寥寥无几，第二天课堂上，教师邀请了一位得到了正确解答的同学来阐述他的解题思路。他的解答是这样的：

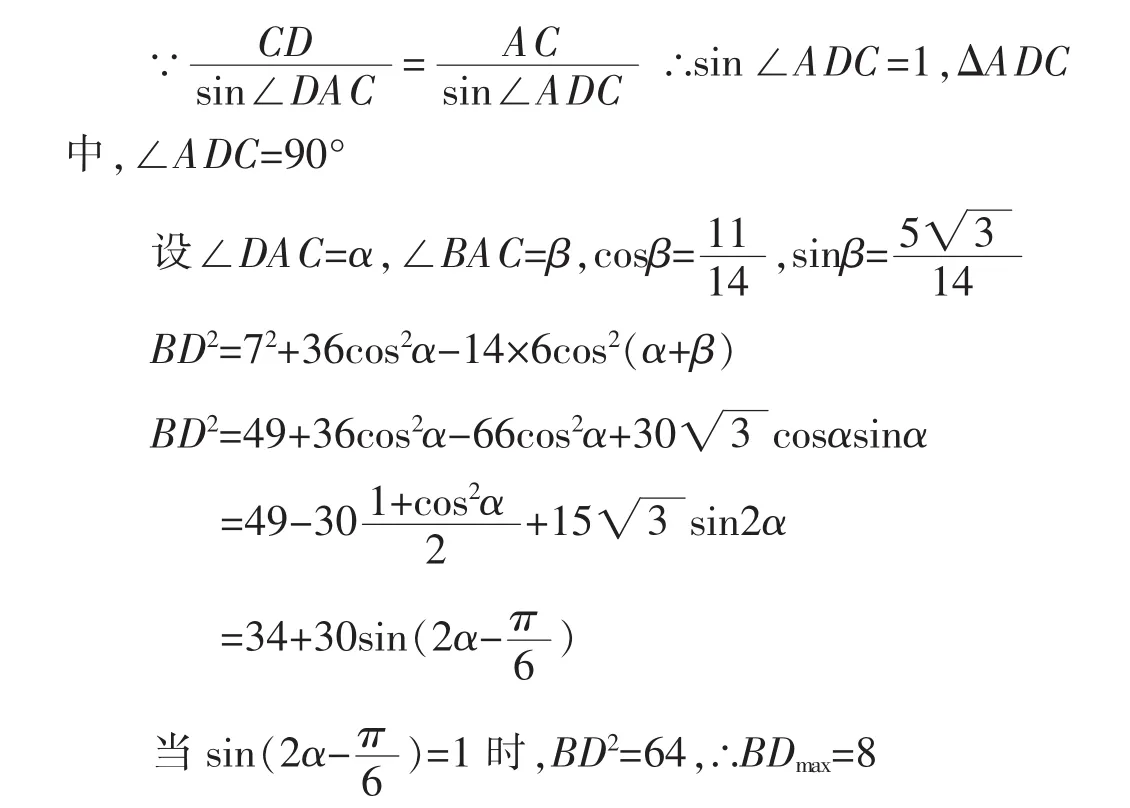
大胆假设、熟练转化。该生精彩讲演之后，另一名同学举手，提出了更简捷的思路：利用了数形结合的思想，∵∠ADC=90°，不妨作△ADC的外接圆，AC为直径，AC中点为圆心，不难算出cos∠ABC>0，所以∠ABC是锐角，故B点在外接圆外部。∵△ABC可以确定唯一，所以点B是圆外一定点，那么问题就可以看成是圆外一定点B与圆上一动点D之间的距离问题，那么BDmax=d+r=8。

思维火花的碰撞，让学生学习到了更多课本给不了的知识，教师演示、强调多次的数形结合思想，不如这两位学生的灵活运用给其他同学带来的直观感受强烈。

即使在同一课堂下，各人的吸收与反馈不尽相同，对于知识点的理解和应用熟练程度也有所不同。一道题出现，每个人都会选择自己熟悉的、简便的方法去完成。教师应充分利用这一特点，将能进行一题多解的例题搬上讲台，让学生在课堂讨论、碰撞，发挥所长。这样不仅能让学生彼此补充、相互学习、拓展眼界，还能提高学生的自信，激发他们从更多角度去思考和发现问题，从而达到高效课堂的目的。

三、恰当改编，一题多变感悟深

有些题目虽然结构形态相似，解决的思维方式却不尽相同。课堂的时间有限，考察的内容却是多样的，教师应当注重对教材或者其他材料的“二次开发”，可以通过适当的改编，让一道题呈现不同的考点，让学生集中解决一类多样的问题，能够更好地帮助他们强化审题和辨析能力［1］。

在微积分定理的复习课上，教师选用了一道书本改编题：例3：求x=y2与y=x-2所围成的曲边梯形面积。根据①作图②找点③写积分式④计算的基本步骤，学生根据以往知识可以较容易的得到的积分式，并根据牛顿-莱布尼茨公式进行计算。

在大部分学生完成之后，教师提出是否有其它方式解决该题，让学生思考几分钟后，引导学生用y型积分式表示该曲边梯形面积：，该方法显然比x型更加简便、易计算。为加深学生对积分的理解，教师提出了两道变式：

变式1：求y=x-2与y=-1与y=2与y轴围成的图形，绕y轴旋转一周，得到的圆台体积。

从积分的定义入手，教师指导学生梳理积分相关知识并得出结论。

变式2：求y=x-2与x=y2围成的曲边梯形，绕y轴旋转一周得到的几何体体积。

本题是变式1的深化，可以让学生在充分掌握变式1后进行独立思考与演练，再由教师指导作答：

若课堂时间不允许，教师亦可将其作为课堂的“留白”，让学生在课下就此类问题进行归纳、回味和升华。

一道例题，两道变式，由浅入深、层层递进，将微积分知识进行了较全面的涵盖与深化。例题是帮助学生累积经验的一种重要手段，相关题组的讲解和训练，能够帮助学生提高转化和化归的能力，激发学生的认知兴趣和解题能力。教师不应只局限于书本或者练习给的例题，生搬硬套［3］。挖掘和整合，适当的编排，能够升华一道题的品质和功能。

四、巧设练习，“例”从生来

例题从何而来？书本？讲义？还是网络？

在与学生讨论直线与圆相切的位置关系时，教师先是在课堂上给学生出了这样一道练习，邀请了一位平时成绩中上的同学上台板演：

例4.圆的方程为x2+y2-2x-2y+1=0，过点P（2，4）作圆的切线，求切线方程。

这个同学经过一番思考后在黑板上写下了如下过程：

设直线方程为y-4=k（x-2），

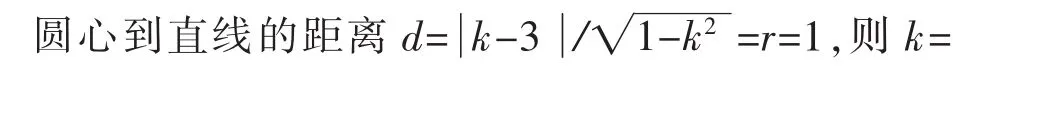
这位学生下台后，教师首先肯定学生的板书与思路，利用直线与圆相切时圆心到直线距离等于半径这一性质解决问题。但教师马上又提出疑问：P点与圆的位置关系是怎样的？

生：P点在圆外。

师：过圆外一点可以作几条圆的切线呢？

生：两条。

师：那么另外一条去哪了？我们漏了什么情况？

学生马上反应过来，原来是把直线斜率不存在的情况漏了。

于是教师再次邀请了刚才的同学上来补充，他的补充如下：

若直线斜率不存在，则直线方程为x=2，圆心（1，1）到直线的距离为2-1=r

∴x=2与圆相切，

∴切线方程为x=2或3y-4x-4=0.

至此这道题才算完整解决。

教师马上总结：过圆上一点有且仅有一条直线与圆相切，过圆外一点做圆切线有两条，大家在做题时应牢记这个性质，充分考虑直线斜率的存在性讨论。课堂的主角是学生，教师需要有熟练的基本功和丰富的经验才能把控课堂，引导学生［3］。这样的教学片断其实并非偶然，而是教师根据平时积累的教学经验，预设到学生的认知漏洞，而特别设计的，旨在让学生自己犯错，自己纠正，以错为鉴，真正理解和掌握该方面的知识。

例题不一定要生硬地写在教材或者讲义上，它可以生动地出现在课堂的每一个环节，学生的习作，生活的常识都可以作为数学课上值得思考和学习的例题，这样灵活的教学，能很好帮助学生加深印象，理解知识，掌握方法。

充分的例题讲解是学生高效学习的前提，无论是课本还是讲义的例题，教师都应认真对待，探析所要考察的目标和所想展示的思维过程。通过合理的整合、编排、应用，将例题蕴含的思想方法，包含的计算技巧，强化的理论概念都完整的挖掘与利用，鼓励学生进行大胆的思考和推理，培养他们的数学能力和数学核心素养。

［1］梁栋，朱鸿玲.数学概念二次教学的实践与思考——以一道例题的教学为例［J］.数学教育学报，2015（2）.

［2］蒋昊.少做“侦察兵”多做“参谋长”——课堂教学“留白”策略的思考及实践［J］.福建中学数学，2011（10）.

［3］洪玮.课标课程背景下数学课堂教学有效性的思考［J］.福建中学数学，2007（10）.

G632.4

A

1673-9884（2016）09-0120-03

2016-05-30

于倩倩（1987-），女，福建福州人，福州市第十八中学二级教师。